Forced Vibration Analysis of Euler-Bernoulli Double-Beam Systems by Means of Green’s Functions
-
摘要:
双曲梁系统通常出现在许多工程领域。与双直梁系统相比,该系统在噪声和振动控制问题上的效率更高。该文采用经典的Euler-Bernoulli曲梁模型来模拟双曲梁系统,通过Green函数和Laplace变换方法得到双曲梁系统稳态受迫振动的闭合形式解,该解可用于任何边界条件。在数值部分,通过与参考文献中的一些结果进行比较来验证本方案的解。讨论了一些重要的几何和物理参数对振动响应的影响以及弹性层刚度与双曲梁系统之间的相互作用。结果表明,梁的半径趋于无穷大时,双曲梁系统退化为双直梁系统,此外,双曲梁系统也可以简化为一个直梁和一个曲梁的组合形式。
-
关键词:
- Green函数 /
- Euler-Bernoulli梁模型 /
- 双曲梁系统 /
- Winkler型弹性层 /
- Laplace变换
Abstract:Double-curved-beam (DCB) systems are usually seen in many engineering fields. Compared to straight double-beam systems, DCB systems are more efficient in noise and vibration control problems. To obtain closed-form solutions of steady-state forced vibrations of DCB systems, the classical Euler-Bernoulli curved beam (ECB) model was employed to model vibration equations for the DCB systems. Green’s functions and the Laplace transform methods were used to get the closed-form solutions to the vibration equations for the DCB systems. These solutions apply to arbitrary boundary conditions. Numerical tests were conducted to verify the present solutions with related results from previous literatures. Effects of some important geometric and physical parameters on vibration responses and the interaction between the elastic layer stiffness and the DCB system, were discussed. The results show that, the DCB system will degenerate to a straight double-beam system when the 2 radii approach infinity, moreover, the DCB system can be simplified as one comprising a straight beam and a curved beam.
-
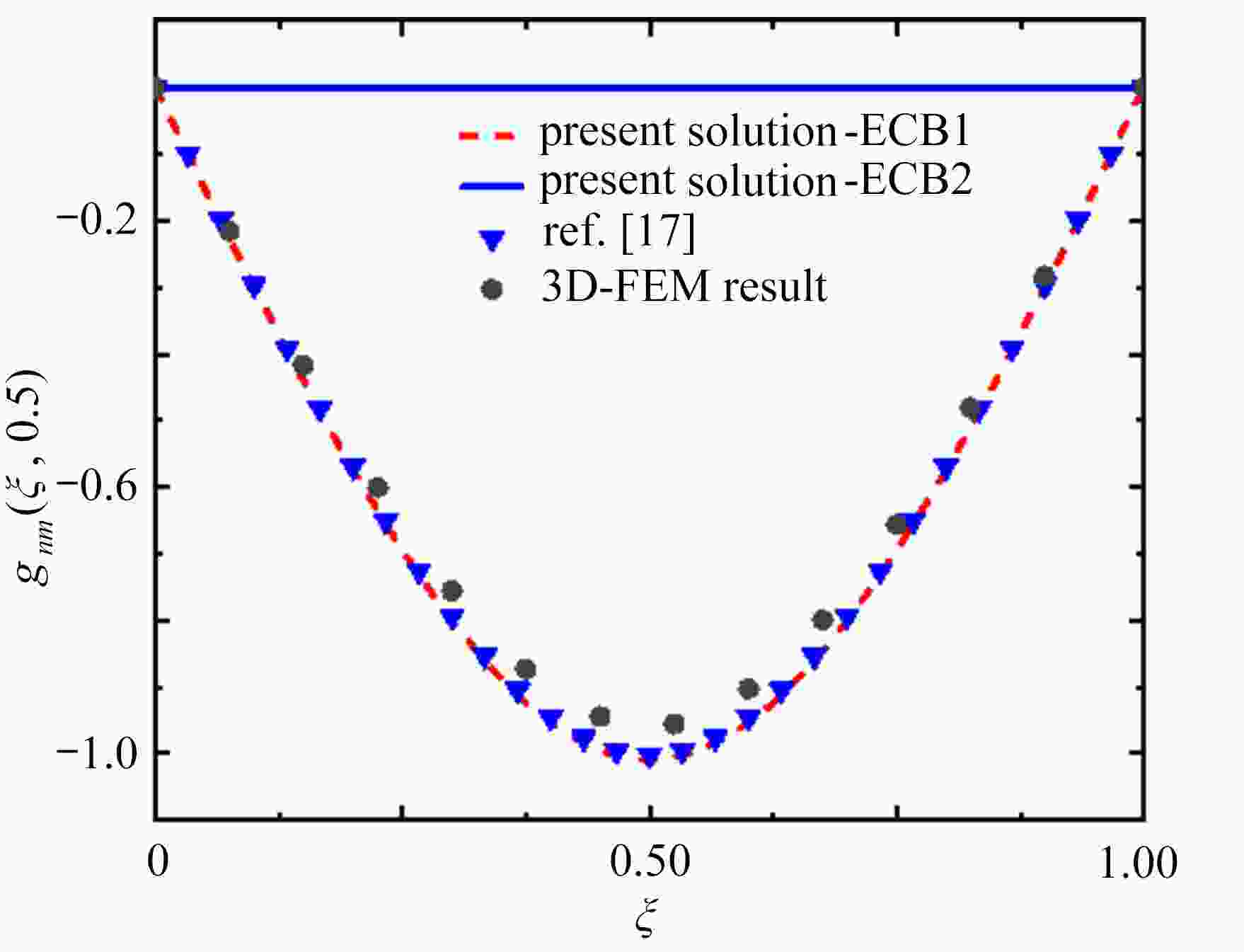
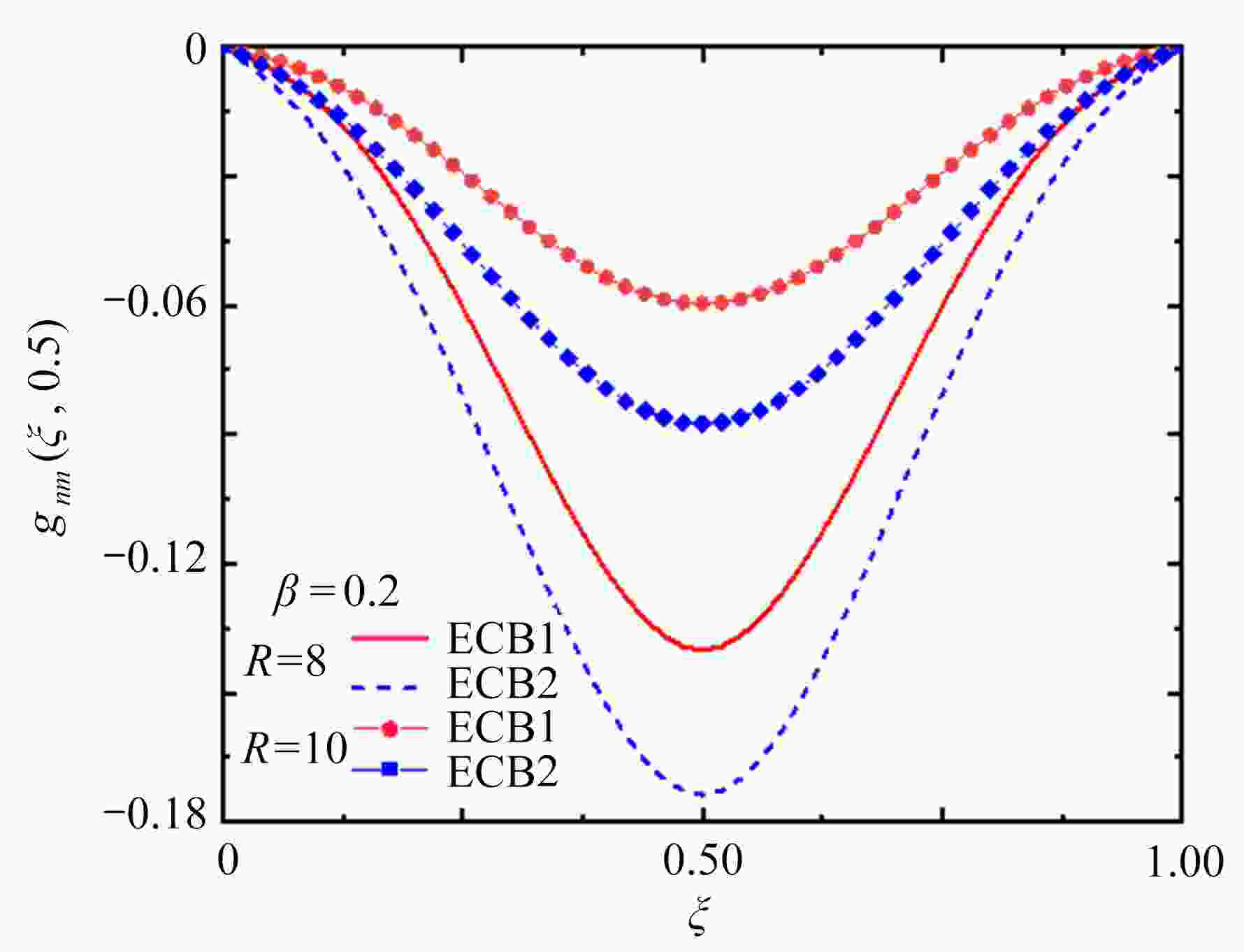
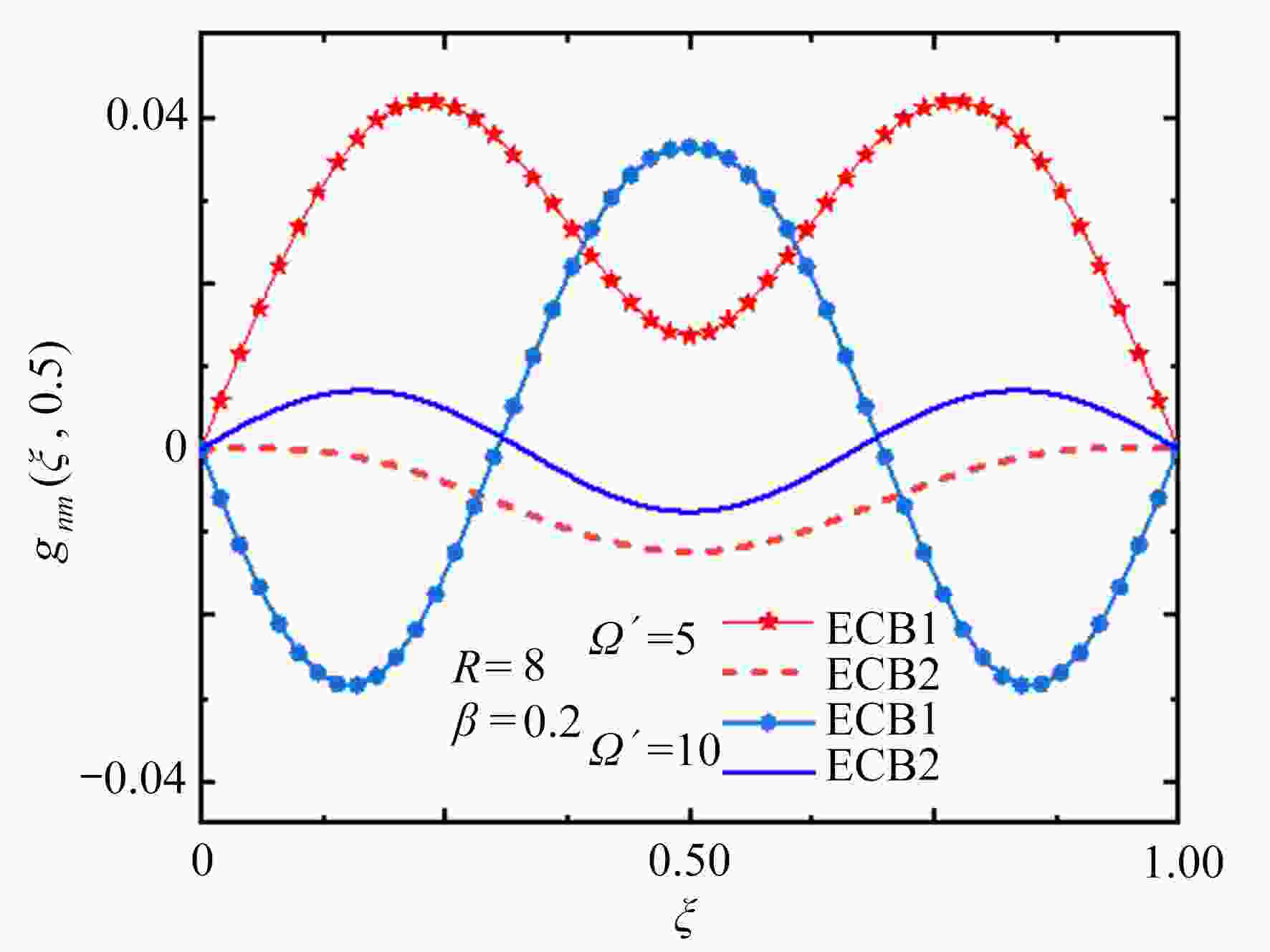
图 5 不同半径相同弹性层弹性模量和相同外激励下双曲梁的无量纲化位移
$g_{nm}( \xi$ , 0.5)(n=1, m=1, 2)$({K_0} = 0.1$ ,$\varOmega ' = {\text{0}}.5)$ Figure 5. Dimensionless Green’s function
$g_{nm}( \xi$ , 0.5)(n=1, m=1, 2) as a function of dimensionless coordinate$x$ for different radius values$({K_0} = 0.1$ ,$\varOmega ' = {\text{0}}.5)$ 表 1 双曲梁的不同边界条件
Table 1. Boundary conditions (BCs) of the DCB
BC beam ECB pinned upper beam ${W_1}\left| {_{x = 0,L} } \right. = 0,{\text{ } }{\lambda _{15} }W_1^{\left( 4 \right)} + {\lambda _{ {\text{16} } } }W_1^{\prime \prime }\left| {_{x = 0,L} } \right.{\text{ = 0, } }{\lambda _{ {\text{11} } } }W_1^{\left( 5 \right)} + {\lambda _{ {\text{12} } } }W_1^{\prime \prime \prime } + {\lambda _{ {\text{13} } } }W_1^\prime + {\lambda _{ {\text{14} } } }W_2^\prime \left| {_{x = 0,L} } \right. = 0$ bottom beam ${W_{\text{2} } }\left| {_{x = 0,L} } \right. = 0,{\text{ } }{\lambda _{ {\text{25} } } }W_{\text{2} } ^{\left( 4 \right)} + {\lambda _{ {\text{26} } } }W_{\text{2} }^{\prime \prime }\left| {_{x = 0,L} } \right.{\text{ = 0, } }{\lambda _{ {\text{21} } } }W_{\text{2} }^{\left( 5 \right)} + {\lambda _{ {\text{22} } } }W_{\text{2} }^{\prime \prime \prime } + {\lambda _{ {\text{23} } } }W_{\text{2} }^\prime + {\lambda _{ {\text{24} } } }W_{\text{1} } ^\prime \left| {_{x = 0,L} } \right. = 0$ fixed upper beam ${W_1}\left| {_{x = 0,L} } \right. = 0,{\text{ } }W_1^\prime \left| {_{x = 0,L} } \right.{\text{ = 0, } }{\lambda _{ {\text{11} } } }W_1^{\left( 5 \right)} + {\lambda _{ {\text{12} } } }W_1^{\prime \prime \prime }\left| {_{x = 0,L} } \right. = 0$ bottom beam $W_2\left| {_{x = 0,L} } \right. = 0,{\text{ } }W_2^\prime \left| {_{x = 0,L} } \right.{\text{ = 0, } }{\lambda _{ {\text{21} } } }W_1^{\left( 5 \right)} + {\lambda _{ {\text{22} } } }W_1^{\prime \prime \prime }\left| {_{x = 0,L} } \right. = 0$ free upper beam $W_1^{\prime \text{}\prime }|{}_{x=0,L}=0,\text{ }W_1^{\prime \text{}\prime \text{}\prime }|{}_{x=0,L}\text{=0, }{\lambda }_{11}W_1^{\left( 5 \right)} + {\lambda }_{13}W_1^{\prime } + {\lambda }_{14}W_2^{\prime }|{}_{x=0,L}=0$ bottom beam $W_2^{\prime \text{}\prime }|{}_{x=0,L}=0,\text{ }W_2^{\prime \text{}\prime \text{}\prime }|{}_{x=0,L}\text{=0, }{\lambda }_{21}W_2^{\left( 5 \right)} + {\lambda }_{23}{W}_2^{\prime } + {\lambda }_{24}{W}_1^{\prime }|{}_{x=0,L}=0$ -
[1] 王静平, 葛仁余, 牛忠荣, 等. 质量-弹簧装置连接的双梁结构固有频率计算[J]. 应用力学学报, 2020, 37(2): 833-839WANG Jingping, GE Renyu, NIU Zhongrong, et al. Natural frequency calculation of a double-beam system joined by a mass-spring device[J]. Chinese Journal of Applied Mechanics, 2020, 37(2): 833-839.(in Chinese) [2] 韩飞, 淡丹辉, 赵磊, 等. 一类浅垂度倾斜双梁系统动力特性研究[J]. 振动工程学报, 2019, 32(1): 140-150HAN Fei, DAN Danhui, ZHAO Lei, et al. Dynamic characteristic research on the double-beam system with shallow sag and inclination[J]. Journal of Vibration Engineering, 2019, 32(1): 140-150.(in Chinese) [3] ONISZCZUK Z. Forced transverse vibrations of an elastically connected complex simply supported double-beam system[J]. Journal of Sound and Vibration, 2003, 264(2): 273-286. doi: 10.1016/S0022-460X(02)01166-5 [4] ONISZCZUK Z. Free transverse vibrations of elastically connected simply supported double-beam complex system[J]. Journal of Sound and Vibration, 2000, 232(2): 387-403. doi: 10.1006/jsvi.1999.2744 [5] ZHANG Y Q, LU Y, WANG S L, et al. Vibration and buckling of a double-beam system under compressive axial loading[J]. Journal of Sound and Vibration, 2008, 318(1/2): 341-352. [6] WU Y, GAO Y. Dynamic response of a simply supported viscously damped double-beam system under the moving oscillator[J]. Journal of Sound and Vibration, 2016, 384: 194-209. doi: 10.1016/j.jsv.2016.08.022 [7] STOJANOVIĆ V, KOZIC P. Forced transverse vibration of Rayleigh and Timoshenko double-beam system with effect of compressive axial load[J]. International Journal of Mechanical Sciences, 2012, 60(1): 59-71. doi: 10.1016/j.ijmecsci.2012.04.009 [8] ZHAO X, CHEN B, LI Y H, et al. Forced vibration analysis of Timoshenko double-beam system under compressive axial load by virtue of Green’s functions[J]. Journal of Sound and Vibration, 2020, 464: 115001. doi: 10.1016/j.jsv.2019.115001 [9] 卜万奎, 徐慧, 赵玉成. 基于曲梁弹性理论的弯曲覆岩变形及应力分析[J]. 应用数学和力学, 2020, 41(3): 302-318BU Wankui, XU Hui, ZHAO Yucheng. Analysis on deformation and stress of bending stratum based on the elastic theory for curved beams[J]. Applied Mathematics and Mechanics, 2020, 41(3): 302-318.(in Chinese) [10] 袁嘉瑞, 丁虎, 陈立群. 微曲输流管道振动固有频率分析与仿真[J]. 应用数学和力学, 2022, 43(7): 719-726YUAN Jiarui, DING Hu, CHEN Liqun. Analysis and simulation of natural frequencies of slightly curved pipes[J]. Applied Mathematics and Mechanics, 2022, 43(7): 719-726.(in Chinese) [11] 吕和祥, 唐立民, 刘秀兰. 曲梁单元和它的收敛率[J]. 应用数学和力学, 1989, 10(6): 487-498 doi: 10.1007/BF02017892LÜ Hexiang, TANG Limin, LIU Xiulan. The curved beam element and its convergence rate[J]. Applied Mathematics and Mechanics, 1989, 10(6): 487-498.(in Chinese) doi: 10.1007/BF02017892 [12] 赵迎港, 杨宇威, 赵颖涛, 等. 关于薄壁曲梁与直梁解析解的进一步讨论[J]. 力学与实践, 2022, 44(5): 1189-1194ZHAO Yinggang, YANG Yuwei, ZHAO Yingtao, et al. Further discussion on the analytical solutions to curved beam and straight beam[J]. Mechanics in Engineering, 2022, 44(5): 1189-1194.(in Chinese) [13] 乔丕忠, 黄思馨, 李志敏, 等. 薄壁曲梁的稳定性研究进展[J]. 力学季刊, 2020, 41(3): 385-400QIAO Pizhong, HUANG Sixin, LI Zhimin, et al. Advances in stability analysis of thin-walled curved beams[J]. Chinese Quarterly of Mechanics, 2020, 41(3): 385-400.(in Chinese) [14] SHIN Y J, KWON K M, YUN J H. Vibration analysis of a circular arch with variable cross-section using differential transformation and generalized differential quadrature[J]. Journal of Sound and Vibration, 2008, 309(1/2): 9-19. [15] SOBHANI E, MASOODI A R. Differential quadrature technique for frequencies of the coupled circular arch-arch beam bridge system[J]. Mechanics of Advanced Materials and Structures, 2022. DOI: 10.1080/15376494.2021.2023920. [16] STOJANOVIĆ V, PETKOVIC M, MILIĆ D. Nonlinear vibrations of a coupled beam-arch bridge system[J]. Journal of Sound and Vibration, 2019, 464: 115000. [17] ZHAO X, LI S Y, ZHU W D, et al. Nonlinear forced vibration analysis of a multi-cracked Euler-Bernoulli curved beam with inclusion of damping[J]. Mechanical Systems and Signal Processing, 2022, 180: 109147. doi: 10.1016/j.ymssp.2022.109147 [18] 赵翔, 周扬, 邵永波, 等. 基于Green 函数法的Timoshenko 曲梁强迫振动分析[J]. 工程力学, 2020, 37(11): 12-27ZHAO Xiang, ZHOU Yang, SHAO Yongbo, et al. Analytical solutions for forced vibrations of Timoshenko curved beam by means of Green’s functions[J]. Engineering Mechanics, 2020, 37(11): 12-27.(in Chinese) -






 下载:
下载: