ⓒ 应用数学和力学编委会,ISSN 1000-0887
近年来,随机微分方程理论得到了快速发展,该理论被广泛应用于经济、金融、生物、控制、优化等领域.在局部Lipschitz和线性增长条件下,随机微分方程存在唯一解,但一般情况下,解无显式表达式.人们通常用数值逼近的方法来给出真实解的一些刻画.在逼近时,要求数值解有一定的稳定性.
许多学者研究了随机微分方程带非随机步长(即步长与ω无关)数值解的稳定性.文献[1]给出了θ-隐式数值解,并得到了数值解的几乎处处稳定性.文献[2]用经典的EM数值解逼近非线性随机延迟微分方程,得到了数值解的几乎处处指数稳定性;在真实解几乎处处稳定的情况下,对漂移项再加一个线性增长的条件,也得到数值解几乎处处稳定.文献[3]研究了随机泛函微分方程,得到了当真实解几乎处处稳定时,经典的EM数值解也几乎处处稳定.文献[4]研究了中立随机泛函微分方程的数值解,在局部Lipschitz和线性增长条件下,得到了经典的EM数值解在均方意义上强收敛到真实解,还得到了收敛的速度.文献[5]研究了在固定时刻延迟的中立随机微分方程的数值解,在多项式增长条件下,得到了经典的EM数值解在均方意义上强收敛到真实解且给出了收敛速度.文献[6]研究了在固定时刻延迟的带马氏切换的中立随机微分方程,在真实解稳定于0的前提下,得到了经典的EM数值解几乎处处稳定于平凡解.文献[7]研究了带Poisson(泊松)跳的中立延迟随机微分方程,得到了经典的EM数值解收敛到真实解.文献[8]研究了中立随机方程,得到了倒项的EM(BEM)数值解与真实解的几乎处处渐近稳定性.文献[9-13]研究了几类随机微分方程真实解的几乎处处稳定性,为以上不同模型数值解稳定性的证明提供了有用的证明技巧.
当随机微分方程的系数满足全局Lipschitz条件时,如果真实解几乎处处稳定,那么经典的显式数值解(比如EM数值解)也几乎处处稳定.当系数不满足全局Lipschitz条件时,带固定步长的EM数值解可能不是几乎处处稳定的(见文献[14]中引理3.1).隐式数值解可以克服此困难.与显式数值解相比,隐式数值解对步长要求不太严格,而且对很多随机微分方程来说,只要真实解有稳定性,隐式数值解也有稳定性.然而,对非线性方程,隐式数值解在每一步迭代时计算量非常大.
目前提出的带随机步长的EM数值方法引起了广泛的关注,文献[15]首次给出了随机微分方程带随机步长EM数值解,得到了数值解几乎处处稳定于0.带随机步长的EM数值解在每一步都修正了步长,从而能控制局部误差,使得在计算时可以减少一些迭代,因此减少了计算量.此外,带随机步长的EM方法比非随机步长的EM方法对漂移项和扩散项的要求条件要弱,不需要全局Lipschitz条件,因此应用范围更广.修正每一步步长的技巧已经被广泛用于多阶段方法.
现实生活中,很多系统不可避免地要考虑随机噪声和延迟的影响.状态空间依赖于过去的系统,可以用随机泛函微分方程来描述.本文将研究随机泛函微分方程带随机步长的EM数值解,由非负半鞅的收敛定理,得到数值解稳定于平凡解.本文结构如下:第1节给出一些数学符号、引理和预备定理;第2节介绍带随机步长的EM算法;第3节给出本文的主要结果即定理2,首先证明步长选择的合理性,给出停时的证明,得到带随机步长EM方法的几乎处处渐近稳定性;第4节给出一个例子;第5节给出本文的结论.
令|·|表示Rn中的欧氏范数.若A是一个向量或矩阵,AT表示A的转置.〈x,y〉或xTy表示x,y在Rn上的内积.令a∨b=maxa,b和a∧b=mina,b.用「x⎤表示大于x的最小整数,N代表非负整数集,Z代表整数集,Q表示有理数集,R+=[0,∞),a.s.表示几乎处处成立,即除了一个零概率集外成立.
(Ω,F,Ft,P)是满足一般条件的带流Ftt≥0的完备概率空间,即Ftt≥0右连续递增且F0包括所有的P-零测集.设τ>0,C([-τ,0],Rn)表示从[-τ,0]到Rn上的连续函数族,若φ∈C([-τ,0],Rn),定义![]() 表示一族在[-τ,0]上连续有界、关于F0可测的Rn值的随机过程.ω(t)是定义在概率空间上的m维Brown(布朗)运动.
表示一族在[-τ,0]上连续有界、关于F0可测的Rn值的随机过程.ω(t)是定义在概率空间上的m维Brown(布朗)运动.
设f:C([-τ,0];Rn)→Rn,g:C([-τ,0];Rn)→Rn×m都是Borel-可测泛函,考虑如下定义的随机泛函微分方程:
(1)
其中,xt=x(t+θ):-τ≤θ≤0为一个C([-τ,0],Rn)-值的随机过程.显然,当θ=0时,xt(θ)=x(t+θ)=x(t).式(1)的初始值为![]() 为了保证式(1)的解的存在唯一性,对系数加以下条件.
为了保证式(1)的解的存在唯一性,对系数加以下条件.
假设1(局部Lipschitz条件) 对于每个k≥1,存在一个正的常数Ck,对任意的φ,ψ∈C([-τ,0];Rn),且‖φ‖∨‖ψ‖≤k,有
(2)
假设2(单调条件) 对任意的φ∈C([-τ,0];Rn),有
(3)
易知当假设1、2成立时,对任意给定的初始值xi,方程(1)存在唯一解.若z(φ)=0当且仅当φ(0)=0或φ≡0成立,则-z(0)![]() |g(0)|2≤0,从而g(0)=0;此外,若φ不恒等于0且φ(0)≠0,f(φ)=0,则-z(φ)
|g(0)|2≤0,从而g(0)=0;此外,若φ不恒等于0且φ(0)≠0,f(φ)=0,则-z(φ)![]() |g(φ)|2≤0,从而z(φ)=0,这与z(φ)=0当且仅当φ(0)=0或φ≡0成立矛盾,因此,若φ不恒等于0且φ(0)≠0,则f(φ)≠0 .为了保证初值为0时,方程(1)存在平凡解,还须假定f(0)=0.
|g(φ)|2≤0,从而z(φ)=0,这与z(φ)=0当且仅当φ(0)=0或φ≡0成立矛盾,因此,若φ不恒等于0且φ(0)≠0,则f(φ)≠0 .为了保证初值为0时,方程(1)存在平凡解,还须假定f(0)=0.
定理1(见文献[10]的定理2.2) 若假设1、2成立,且z(φ)=0当且仅当φ(0)=0或φ≡0,那么对任意有界的初始值ξ∈C([-τ,0];Rn),有limt→∞x(t)=0,a.s..
在介绍EM数值解之前,首先给出以下离散半鞅收敛定理.
引理1 让Akk∈N和Ukk∈N是两列非负的Fk-可测的随机序列,k=0,1,2,…,A0=U0=0,a.s.,Mk是一个实值局部鞅且M0=0,a.s.,ζ是一个非负F0-可测的随机变量.假设一个非负随机过程Xk可分解为如下形式:
Xk=ζ+Ak-Uk+Mk,
若limk→∞Ak<∞几乎处处成立,那么对所有的ω∈Ω,几乎处处地有limk→∞Xk<∞,limk→∞Uk<∞, 即Xk和Uk几乎处处收敛到有限的随机变量.
设M∈N,M>τ.令Δ=τ/M∈(0,1)为固定步长,t0=0,t-1=-Δ,t-2=-2Δ,…,t-M=
-MΔ=-τ.定义
(4)
易知
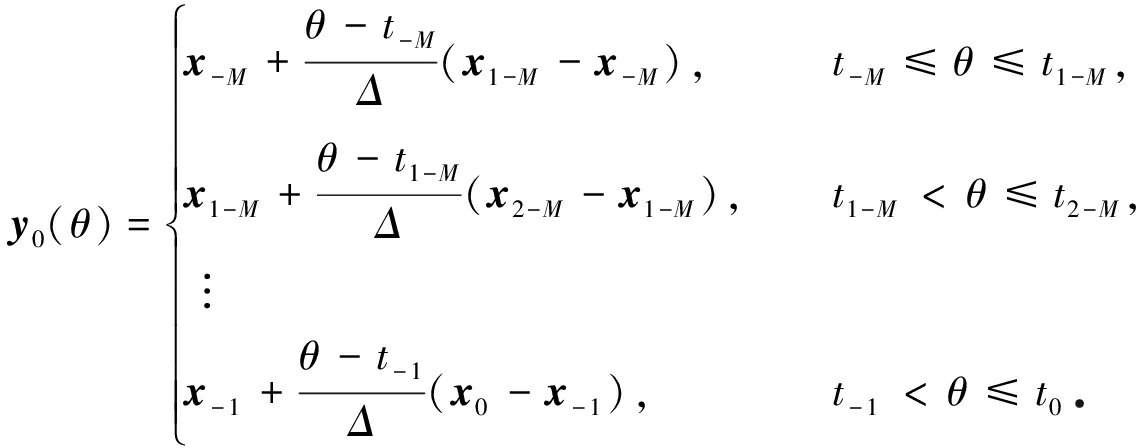
若‖y0‖≠0,则取
若‖y0‖=0,则取
Δt0=2-2.对任意的k=-M,-M+1,…,-1,0,xk=ξ(tk)关于F0可测,由y0的表达式可知,y0关于F0可测,从而Δt0关于F0可测,又t0=0,令t1=t0+Δt0,则t1关于Ft0可测.定义
y1![]()
![]() 易知
易知
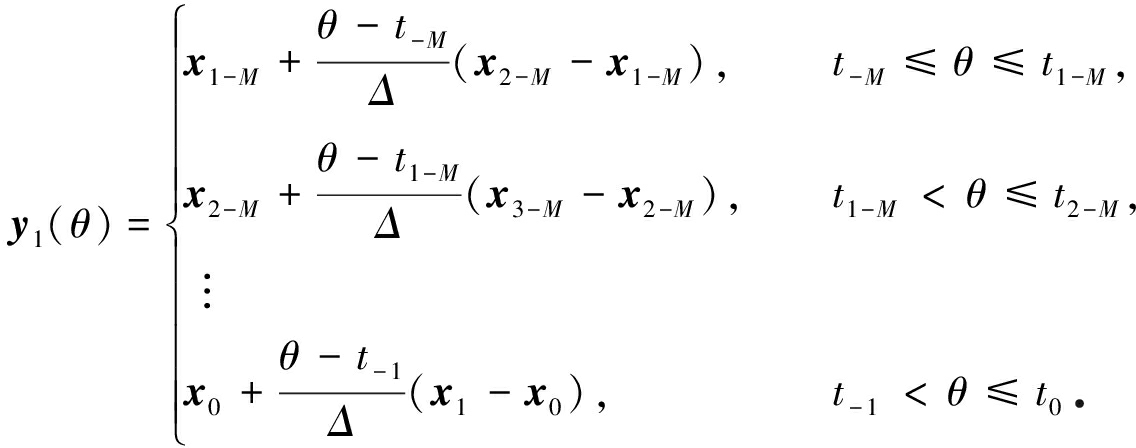
若‖y1‖≠0,则取
若‖y1‖=0,则取Δt1=2-2.t2=t1+Δt1,由于x0,f(y0)Δt0,g(y0)ωt0关于F0可测,ωt1关于Ft1可测,故x1关于Ft1可测.又x0,x-1,…,x1-M关于F0可测,从而x1,x0,…,x1-M关于Ft1可测.因此,由y1的表达式可知,y1关于Ft1可测,从而Δt1关于Ft1可测.令t2=t1+Δt1,定义
一般地,当k≥0时,定义
(5)
其中yk是用线性插值定义的随机过程:
(6)
ti≤θ≤ti+1,i=-M,-M+1,…,-1.Δωtk=ωtk+1-ωtk是Brown运动在[tk,tk+1]上的增量.若‖yk‖≠0,则取
若‖yk‖=0,则取Δtk=2-2.Δtk依赖于yk,yk依赖于xk+i+1,i=-M,-M+1,…,-1,类似于前面的推导可知xk+i+1关于Ftk+i+1可测,从而关于Ftk可测,故yk关于Ftk可测,从而随机步长Δtk关于Ftk可测.称由式(4)和(5)定义的xk![]() 为带随机步长的EM数值解.令
为带随机步长的EM数值解.令![]()
首先强调两个关于随机步长的重要性质.第一,有限个步长求和是停时,停时主要用于定理2中局部鞅的证明;第二,可列无限多个步长求和是发散的,发散可以保证时间趋于无穷.本文主要结果如下.
定理2 在假设1、2成立条件下,若z(φ)=0当且仅当φ(0)=0或φ≡0,且
(7)
成立,则![]() 是Ft停时,
是Ft停时,![]() 且对任意有界的初值ξ∈C([-τ,0];Rn)有
且对任意有界的初值ξ∈C([-τ,0];Rn)有
证明 由式(5)可得
(8)
这里 Δmk=2〈xk+f(yk)Δtk,g(yk)Δωk〉+![]() (
(![]() -Δtk).
-Δtk).
下面分3步证明该定理,第一步证明随机步长选择的合理性以及tk是Ft停时.第二步证明对任意的![]() 是局部鞅.第三步给出随机步长序列的发散性,从而得到xk几乎处处稳定于平凡解.
是局部鞅.第三步给出随机步长序列的发散性,从而得到xk几乎处处稳定于平凡解.
步骤1 由式(3)可知,在每一步都可以选择充分小的有理步长Δtk,使其满足
(9)
事实上,当‖yk‖≠0时,选择Δtk=2-nk,nk=「1-log2(z(yk)/![]() )⎤,注意到nk>1-log2(z(yk)/
)⎤,注意到nk>1-log2(z(yk)/![]() ),因此Δtk=2-nk≤(1/2)(z(yk)/
),因此Δtk=2-nk≤(1/2)(z(yk)/![]() ),由单调条件知-U(yk,Δtk)≤-(1/2)z(yk)≤0,从而式(9)成立;当‖yk‖=0时,yk=0,由条件知z(yk)=z(0)=0,f(yk)=f(0)=0,Δtk=2-2,因此,-U(yk,Δtk)=0,从而式(9)成立.
),由单调条件知-U(yk,Δtk)≤-(1/2)z(yk)≤0,从而式(9)成立;当‖yk‖=0时,yk=0,由条件知z(yk)=z(0)=0,f(yk)=f(0)=0,Δtk=2-2,因此,-U(yk,Δtk)=0,从而式(9)成立.
下面由归纳法证tk是Ft停时.当k=0时,tk=t0=0,结论显然成立.假设tk关于Ft为停时,即对任意t≥0,有tk≤t∈Ft,对任意s∈Z,j∈N,2sj∈[0,t],有tk≤2sj∈F2sj⊆Ft,由第2节的分析知Δtk关于Ftk可测,从而Δtk≤t-2sj∈Ftk⊆F,因此有tk≤2sj∩Δtk≤t-2sj∈Ft.因为Z,N是可数集,所以有对任意的t≥0,
即tk+1是Ft停时.由数学归纳法可得对任意k≥0,tk是Ft停时.
将式(9)代入式(8),有
对k求和,
(10)
这里![]()
步骤2 注意到yk, Δtk关于Ftk可测,Δωtk关于Ftk+1可测, 由式(5)知,xk+1关于Ftk+1可测.定义一个新的流Gk,Gk=Ftk+1,k=-1,0,1,…,则xk+1关于Gk可测,由式(10)可知mk关于Gk可测.
下面证明mkk≥0是关于流Gk的局部鞅.注意到ξ有界,不妨令R>0,ξ≤R,定义停时
由xk关于Ftk可测知,ρR为Ftk的停时,因此,ρR是Gk-1的停时,即ρR≤k∈Gk-1.由ρR的定义知,对所有的k≥0,有xk∧ρR≤R,a.s..
首先,证明对任意t≥0,tk∧ρR和t(k+1)∧ρR都是Ft停时.对tk∧ρR有
其中ρR≥k=ρR≤k-1c∈Gk-2⊆Gk-1=Ftk.由Ftk的定义可得tk≤t∩ρR≥k∈Ft,又![]() 注意到对j=0,1,…,k-1,ρR=j=ρR≤j-ρR≤j-1∈Gj-1=Ftj.由Ftj的定义可知,tj≤t∩ρR=j∈Ft,所以tρR≤t∩ρR<k∈Ft,因此tk∧ρR≤t∈Ft.同理可得t(k+1)∧ρR是Ft停时.
注意到对j=0,1,…,k-1,ρR=j=ρR≤j-ρR≤j-1∈Gj-1=Ftj.由Ftj的定义可知,tj≤t∩ρR=j∈Ft,所以tρR≤t∩ρR<k∈Ft,因此tk∧ρR≤t∈Ft.同理可得t(k+1)∧ρR是Ft停时.
对任意的k≥ρR,有xk∧ρR=xρR.定义带停时的Brown运动的增量Δωk∧ρR=ω(t(k+1)∧ρR)-ω(tk∧ρR),以及带停时的时间步长Δtk∧ρR=t(k+1)∧ρR-tk∧ρR,由R→∞时,ρR→∞,a.s.,可得到xk+1=xk+f(yk)Δtk+g(yk)Δωtk.因此,这样的定义是有效的.此外,
和
注意到,当ti≤θ<ti+1,i=-M,…,-1时,有
由ρR的定义可知‖yi∧ρR‖≤R.故由假设1及基本不等式可得
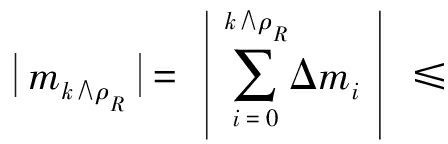
因此
同时
(11)
因为ρR>k=ρR≤kc∈Gk-1,Δωk关于Ftk独立,故关于Gk-1独立,
(12)
(13)
由Δtk+1关于Fk+1=Gk可测及ρR为Gk-1停时,可得
(14)
因此,结合式(12)~(14)可得
代入式(11),有
从而得到mk∧ρRk≥0是关于Gk的鞅,当R→∞时,有ρR→∞.所以mkk≥0是关于Gk的局部鞅.
步骤3 由式(10)及引理1可得
(15)
和
(16)
由式(16)可得limi→∞U(yi,Δti)Δti=0,a.s..下面证明当i→∞时,随机步长Δti不会趋于0,即lim infi→∞Δti>0,a.s..
由式(15)知,对所有ω∈Ω,存在C(ω)∈R+,满足limk→∞|xk(ω)|=C(ω).固定ω,记C(ω)=C.由式(6)知,对任意的θ∈[-τ,0]有limk→∞|yk(θ)|=C.以下分两种情形讨论:
1) 当C≠0时,对任意的θ∈[-τ,0]存在一个充分大的整数![]() 使得对所有的
使得对所有的![]() 因为z(φ)=0当且仅当φ(0)=0或φ≡0,又若φ≠0,则f(φ)≠0,所以在这两个区间上z(yk)≠0,f(yk)≠0.再由z(yk)和f(yk)的连续性可得
因为z(φ)=0当且仅当φ(0)=0或φ≡0,又若φ≠0,则f(φ)≠0,所以在这两个区间上z(yk)≠0,f(yk)≠0.再由z(yk)和f(yk)的连续性可得
所以对任意的![]()
即
由步长的选择可得
因此,
综上,存在![]() 充分大,使得对所有的
充分大,使得对所有的![]() 有Δtk>0,即Δtk永远不会趋于0.
有Δtk>0,即Δtk永远不会趋于0.
2) 当C=0时,设式(7)的极限是D,D>0.存在一个常数δ=δ(D)>0使得对所有的‖φ‖∈(0,δ),有|z(φ)/|f(φ)|2-D|<0.5D.注意到,对任意的θ∈[-τ,0]有
从而可以找到一个充分大的整数![]() 使得对任意的
使得对任意的![]() 有
有
即
由ni=![]()
![]()
![]()
![]() 知
知
因此当i→∞,Δti永远不会趋于0.
综上可得![]() 和limk→∞U(yk,Δtk)=0,a.s..
和limk→∞U(yk,Δtk)=0,a.s..
对充分大的k,若‖yk‖≠0,则由步长Δtk的定义可知Δtk≤z(yk)/(2|f(yk)|2),故由假设2知
U(yk,Δtk)=z(yk)-|f(yk)|2Δtk≥0.5z(yk)≥0,
所以limk→∞z(yk)=0,a.s..由于z(φ)=0当且仅当φ(0)=0或φ≡0,注意到z连续,因此,yk(0)=0或者limk→∞yk=0,a.s..当yk(0)=0时,由t0=0及表达式
可知,xk=0,从而limk→∞xk=0.当limk→∞yk=0,a.s.时,在上述表达式中取θ=ti可得limk→∞xk+i=limk→∞yk(ti)=0,a.s..所以limk→∞xk=0,a.s..
若对充分大的k,‖yk‖=0,则显然有limk→∞xk=0,a.s..证明完成.
随机步长的选择不是唯一的,例如,对任意有理数α∈(0,1),可以令步长Δtk为Δtk=α(z(yk)/|f(yk)|2),同样可以证明结论成立,因此有以下定理.
定理3 在假设1、 2成立的条件下, 若z(φ)=0当且仅当φ(0)=0或φ≡0,z满足式(7).设有理数α∈(0,1).若‖yk‖≠0,取Δtk=α(z(yk)/|f(yk)|2);若‖yk‖=0时,取Δtk为任意有理数.则![]() 是Ft停时,
是Ft停时,![]() 且对任意有界的初值ξ∈C([-τ,0],Rn)有
且对任意有界的初值ξ∈C([-τ,0],Rn)有
考虑如下的一维随机泛函微分方程:
由
易知,f(0)=0,f,g连续,从而满足局部Lipschitz条件,但不满足全局的Lipschitz条件.

z(φ)=0当且仅当φ(0)=0或φ≡0.此外,
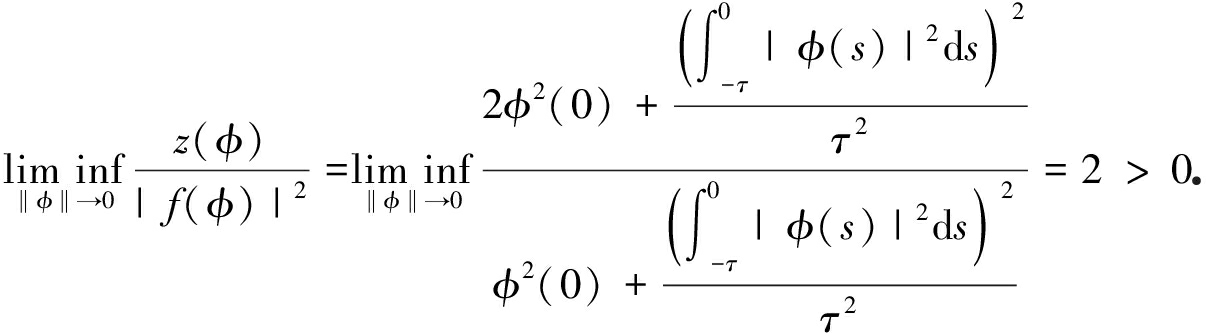
在每一步,选择步长为Δtk=0.5z(yk)/|f(yk)|2,由定理2可得带随机步长的EM数值解几乎处处渐进稳定.
本文研究了带有限延迟的随机泛函微分方程
首次给出了该方程的带随机步长的EM算法,得到了随机步长的两个特点:有限个步长求和是停时;可列无限多个步长求和是发散的.最终由离散形式的非负半鞅收敛定理,得到了在系数满足局部Lipschitz条件和单调条件下,带随机步长的EM数值解几乎处处收敛到0.Liu和Mao(毛学荣)在文献[15]中研究了随机微分方程带随机步长的EM数值解,在一定条件下,得到了数值解几乎处处收敛到0.本文的模型比文献[15]中的模型更一般,因此拓展了文献[15]的结果.
[1] RODKINA A, SCHURZ H. Almost sure asymptotic stability of drift-implicitθ-methods for bilinear ordinary stochastic differential equations inR1[J].Journal of Computational and Applied Mathematics, 2005,180(1): 13-31.
[2] WU F, MAO X R, SZPRUCH L. Almost sure exponential stability of numerical solutions for stochastic delay differential equations[J].Numerische Mathematik, 2010,115(4): 681-697.
[3] WU F, MAO X R, KLOEDEN P E. Almost sure exponential stability of the Euler-Maruyama approximations for stochastic functional differential equations[J].Random Operators and Stochastic Equations, 2011,19(2): 165-186.
[4] WU F, MAO X R. Numerical solutions of neutral stochastic functional differential equations[J].Society for Industrial and Applied Mathematics, 2008,46(4): 1821-1841.
[5] JI Y T, BAO J H, YUAN C G. Convergence rate of Euler-Maruyama scheme for SDDEs of neutral type[J/OL]. [2018-02-06]. https://arxiv.org/abs/1511.07703v2.
[6] MAO X R, SHEN Y, YUAN C G. Almost surely asymptotic stability of neutral stochastic dely differential equations with Markovian switching[J].Stochastic Processes and Their Applications, 2008,118: 1385-1406.
[7] TIAN J G, WANG H L, GUO Y F, et al. Numerical solutions to neutral stochastic delay differential equations with Poisson jumps under local Lipschitz condition[J].Mathematical Problems in Engineering, 2014,2014: 976183.
[8] YU Z H. Almost surely asymptotic stability of exact and numerical solutions for neutral stochastic pantograph equations[J].Abstract and Applied Analysis, 2011,2011: 143079.
[9] MAO X R.Stochastic Differential Equation and Application[M]. Chichester: Horwood Publising, 2007.
[10] MAO X R. LaSalle-type theorems for stochastic differential delay equations[J].Journal of Mathematical Analysis and Applications, 1999,236(2): 350-369.
[11] MAO X R. A note on the LaSalle-type theorems for stochastic differential delay equations[J].Journal of Mathematical Analysis and Applications, 2002,268(1): 125-142.
[12] MAO X R. The LaSalle-type theorems for stochastic functional differential equations[J].Nonlinear Studies, 2000,7(2): 307-328.
[13] MAO X R. Stochastic versions of the LaSalle-type theorems[J].Journal of Differential Equations, 1999,153: 175-195.
[14] HIGHAM D J, MAO X R, YUAN C G. Almost sure and moment exponential stability in the numerical simulation of stochastic differential equations[J].SIAM Journal on Numerical Analysis, 2007,45(2): 592-609.
[15] LIU W, MAO X R. Almost sure stability of the Euler-Maruyama method with random variable stepsize for stochastic differential equations[J].Numerical Algorithms, 2017,74(2): 573-592.