引言
在大数据和人工智能时代,建立能够有效处理复杂数据的模型和算法,以从数据中获取有用的信息和知识是应用数学、统计学和计算机科学面临的共同难题.在数据建模和分析的诸多技术路线中,基于“生成模型”(generative models)的数据分析方法是十分重要的一个研究领域.一般而言,生成模型是指用定量方式来描述数据的生成机制,其核心特征和基本目标是能够从给定的模型出发模拟产生和所研究的实际数据相似的模拟数据.由生成模型模拟产生的数据一般具有多样性,会形成一个数据空间上的概率分布Fθ,其具体形式由模型参数θ所决定.
在不同的学科领域,生成模型呈现出不同的表现形态.在应用数学研究中,数学家常常运用微分方程(differential equations)和动力系统(dynamic systems)等数学工具对产生数据的物理过程进行精细描述[1-5];在统计学研究中,统计学家借助概率分布建立统计模型(statistical models)对观测数据的生成机制进行近似刻画[6-8];在机器学习研究中,人们运用生成对抗网络(generative adversarial networks, GAN)[9]、变分自编码器(variational autoencoders,VAE)[10]等技术手段,通过数据驱动的方式对图像、音频和文本等多种形式数据的产生过程加以人工模拟[11-21].从宏观的角度看,上述这些精细描述、近似刻画、人工模拟数据产生过程的不同方法,都是生成模型的某种具体形式.
上述不同形态的生成模型在建模原则、所用信息、可解释性、稳定性、适用场景等方面有不同的特性.以微分方程和动力系统为代表的“精细模型”(fine models)从微观入手对产生数据的物理过程给予定量刻画,力求细致准确;建模所需的信息以领域知识为主,需要对实际的物理机制有很深的了解;其可解释性较好,但一般仅适用于物理机制清晰明确的工程问题,应用于带有复杂结构的问题时往往面临较大的困难,且比较容易受到噪声的干扰.统计模型则在保留数据核心特征的同时对次要特征和噪声进行简化,以在模型的精准性和复杂性之间达到适当的平衡;通过将领域知识和数据特征相结合的方式来进行建模,可解释性和稳定性较好;一般适用于数据生成机制和噪声模式比较清晰的科学问题,特别是通过实验设计和抽样调查等规范手段收集数据的问题;但需要具体问题具体分析,建模成本较高.以GAN和VAE为代表的“数据驱动生成模型”(data-driven generative models)主要通过数据驱动的方式,从一个很大的模型空间中优化选取适当的模型来完成建模;对领域知识要求较低,适应性强,在图像、音频和文本等数据生成机制用常规方法难以刻画的问题中取得了良好的实际效果;但可解释性和稳定性相对较差.
尽管上述这些生成模型有着多样化的形态和差异化的特性,但是它们都有一个共同的作用:连接数据和科学问题的纽带,将数据转化为有用知识的桥梁.无论是以哪种形态出现的生成模型,其模型参数都在不同程度上或直接或间接地反映了所关心的科学问题的关键信息和核心知识.以生成模型为基础的数据分析,其本质是依据已知的观测数据对未知的模型参数进行推断,从而将数据转化为知识并对所关心的科学问题给予解答.在应用数学和机器学习中,人们常常运用最优化的手段对未知的模型参数进行估计,即在参数空间中找到满足特定最优化准则的最优解来作为未知参数的估计值.在统计学研究中,人们除了关心“最优估计”,还特别关注对未知参数的不确定性进行度量和推断.从科学哲学的角度来看,不确定性度量和推断是一切数据分析都不可避免的一个根本问题.原因在于,尽管“最优解”从某种程度上可以对观测数据给出“最佳”的解释,但是其他非最优解也同样可以对观测数据给出较为合理的解释,因而并不能被决然排除,从而必然给未知参数的推断带来“不确定性”.因而,在一切基于生成模型的数据分析中,不确定性推断都是一个十分重要、不容回避的问题.
相对于单纯的优化,不确定性推断在哲学思辨上要困难很多,技术上也更为复杂.在统计学框架下,有不同的范式来进行不确定性推断,较为常见的是频率学派(frequentist)和Bayes学派(Bayesian).Bayes学派对未知参数设置先验分布(prior distribution),并通过Bayes公式(Bayes formula)对数据似然(data likelihood)实现反转而生成后验分布(posterior distribution).作为参数空间上的一个概率分布,后验分布对未知参数的不确定性进行了完整的刻画;作为给定观测数据的一个条件概率,后验分布充分整合了先验分布和观测数据中所包含的关于未知参数的信息.因而,Bayes框架具有逻辑清晰简明、操作方便快捷的优势,在众多数据分析问题中得到了广泛的应用.然而,经典Bayes分析要求数据似然必须具有明确的解析形式.这一要求一方面给Bayes分析赋予了严格的概率含义,但同时也限制了Bayes分析在许多问题中的应用:在许多复杂的实际问题中,数据似然难以被精确刻画和计算的情况时有发生.本文的第1.3小节将对此类现象给出详细的说明.同时,由于复杂问题中的后验分布大多不再是常规的标准分布,需要通过分布近似或者Monte-Carlo抽样的方式来进行处理和分析,Bayes方法在计算上往往面临较大的挑战.
为了简化Bayes计算,特别是在数据似然难以被精确刻画和计算的情况下运用Bayes框架来进行数据分析,近似Bayes计算(approximate Bayesian computation, ABC)方法进入了人们的视野.ABC方法的思想最初由Rubin在1984年提出[22],随后在许多领域得到了成功的应用,包括群体遗传学(population genetics)研究[23]、考古学(archaeology)[24]、金融建模(financial modelling)[25]、水文模型(hydrological models)[26]、蛋白质网络(protein networks )[27]等.相对于经典的Bayes推断和计算框架,ABC方法的一个重要贡献是在保持了Bayes分析基本框架和概率解释的同时解除了对数据似然精确解析形式的强制依赖.通过从数据中提取特定的统计量,并在统计量之间定义适当的距离来刻画一组新生成数据和观测数据之间的相似性,ABC方法可以在数据似然解析形式不明确的情况下对真实后验分布给出有效近似.ABC方法的这一特性可以将Bayes分析框架从经典的统计模型推广到一般的生成模型,为Bayes分析和人工智能方法的结合提供新的机遇[28-31].
本文将系统介绍和综述ABC方法经典框架和前沿进展,并深入讨论ABC方法与前沿人工智能技术有机结合的思想、方法和应用.本文的剩余部分将按以下的方式安排:第1节简要介绍经典ABC方法的研究背景、基本框架和理论性质;第2节从多个角度综述近年来ABC方法研究的前沿进展;第3节讨论了ABC方法在复杂数据处理,特别是人工智能中的潜在应用;第4节对本文进行总结.
1 经典ABC方法简介
1.1 Bayes推断的基本范式
令yn=(y1,y2,…,yn)代表观测数据集,θ∈Rp表示要学习的参数,p是参数的维度.现实中,观测数据集的生成方式可能十分复杂.统计模型通过对数据的生成方式添加理想化的假设条件达到简化数据生成方式的目的.通常,我们假设yn是随机变量Y的一组实现.并且,随机变量Y服从与θ相关的分布:Y~F(θ),其中分布的概率密度函数由f(·|θ)表示.统计推断是根据观测数据集来推断参数θ的大小.举个例子,假设yn是通过简单随机抽样的方式,在全国范围内收集n个成年人的身高数据.我们的目标是推断全国成年人的平均身高θ∈R.在生物学上,人类的身高可能受到多方面的影响,比如,基因差异、营养水平、气候等.但是,统计模型把身高假设为一个服从正态分布的随机变量.即身高Y~N(θ, σ2),其中σ2是已知量.通过上述假设,统计模型将现实世界的各种因素都包含在统计分布中.
给定上述的统计模型,观测数据集的似然函数可以写为L(θ)=f(yn |θ).频率学派认为θ是一个未知但是固定值;而Bayes学派则把θ当做是一个随机变量,并用一个“先验分布”π0(θ)来表示在观测到数据之前我们对参数θ的先验知识.Bayes推断是基于如下的Bayes公式:
(1)
其中,πn(θ)被称为未知参数θ的“后验分布”,即在观测到数据yn后对未知参数θ的认识.作为参数空间上的一个概率分布,后验分布对未知参数的不确定性进行了完整的刻画;作为给定观测数据的一个条件概率,后验分布充分整合了先验分布和观测数据中所包含的关于未知参数的信息.因而,Bayes框架具有逻辑清晰简明、操作方便快捷的优势,在众多数据分析问题中得到了广泛的应用.
如下定理为Bayes推断给出了基本的理论保证.
定理1 令θ0代表参数的真实值,![]() 代表似然方程的强相合解(strongly consistent solution).定义
代表似然方程的强相合解(strongly consistent solution).定义![]() 并令πn(t|yn)为t的后验分布. 当正则条件(A1)~(A5)成立时,下式以概率1成立:
并令πn(t|yn)为t的后验分布. 当正则条件(A1)~(A5)成立时,下式以概率1成立:
(2)
其中![]()
在参数θ的维度p=1的情况下,正则性条件(A1)~(A5)的具体形式如下:
(A1) 对于所有的θ∈Θ,集合{x|f(x|θ)>0}都是相同的.
(A2) 对数似然函数ln f(x|θ)在区间[θ0-δ,θ0+δ]关于θ三阶可导,Eθ0l(1)(θ0,X)和Eθ0l(2)(θ0,X)都是有界的,且
其中h(i)代表函数h的第i阶导数.
(A3) 积分关于θ满足可交换性,Eθ0l(1)(θ0,X)=0, Eθ0l(2)(θ0,X)=-Eθ0(l(1)(θ0,X))2.并且I(θ0)=Eθ0(l(1)(θ0,X))2>0成立.
(A4) 对于任意δ>0和足够大的n,存在 >0,使得sup|θ-θ0|>δ((ln(θ)-ln(θ0))/n)p<-
>0,使得sup|θ-θ0|>δ((ln(θ)-ln(θ0))/n)p<- 依概率1成立.
依概率1成立.
(A5) 先验分布π0(θ)是连续的,而且在θ0处的密度大于0.
证明 关于定理1的证明可以参考文献[32].
当参数θ是一个低维度向量时,只需将上述正则性条件转化为相应的向量版本即可.由定理1可知:当样本量n增大时,后验分布πn(θ)会越来越集中于真实参数θ0的附近,并且越来越接近于一个正态分布.
在一个实际问题中成功运用Bayes框架来完成数据分析,需要具备如下三个条件:① 要设定适当的先验分布;② 数据似然要具有明确的解析形式;③ 要能够较为便利地利用所得到的后验分布进行不确定性分析和推断.在先验分布的设定上,可以采用“主观先验”(subjective prior)来描述对未知参数的先验知识;也可以用“无信息先验”(noninformative prior),有时也被称作“客观先验”(objective prior),来表达对未知参数没有或者有很弱的先验知识.在统计学文献中,对相关的哲学逻辑、基本原则和实际方法有过大量的思辨和讨论[33-35].在利用后验分布进行推断方面,如果所得到的后验分布是常见的标准分布,则直接进行分析即可;如果得到的后验分布不是常见的标准分布,则可以通过分布近似或者Monte-Carlo抽样[36-39]的方式来进行处理.但对于数据似然具有明确的解析形式这一点,却是经典Bayes分析框架下的基本要求.这一方面给Bayes分析赋予了严格的概率含义,但同时也限制了Bayes分析在许多问题中的应用.在大数据和人工智能时代的许多实际问题中,由于数据和模型的复杂性,数据似然难以被精确刻画和计算的情况时有发生.研究如何在这种情形下利用生成模型进行有效的数据分析和不确定性推断,具有重要的理论和现实意义.
1.2 经典 ABC 方法的基本框架和理论性质
在统计学文献中,ABC方法是解决上述困境的一个重要方法.作为一种可以避免精确计算数据似然的抽样技术,ABC方法的思想最早由 Rubin[22]提出.后经过众多学者[23,40-45]的继承和发展,ABC方法逐渐成为统计学习和Bayes计算的一个重要工具和活跃研究领域.ABC方法的一个核心设定是:尽管真实数据生成过程f(yn|θ)的具体形式未知或者难以精确计算,但是对于任意给定的参数值θ均可构造一个“数据生成器”(data generator)G(z|θ),通过数值计算或者模拟的方式方便地从f(yn|θ)中产生新的样本.算法1给出了经典ABC方法的基本流程.
算法1 ABC算法
算法输入:
(I1) 观测数据yn.
(I2) 模型参数θ的先验分布π(θ).
(I3) 数据生成器G(z|θ).
(I4) 观测数据统计量η(yn).
(I5) 观测数据统计量的距离度量D(η(z),η(z′)).
(I6) 距离门限值δ>0.
算法流程:
(S1) 从先验分布π(θ)中抽取一个候选参数θ*.
(S2) 从数据生成器G(z|θ*)中产生一个合成数据z,并计算其统计量η(z).
(S3) 计算合成数据统计量η(z)与观测数据统计量η(yn)之间的距离D(η(z),η(yn)),如果D(η(z),η(yn))≤δ则将θ*接受并保留,否则丢弃.
(S4) 重复步骤(S1)~(S3),直到算法的终止条件被满足.
算法输出:
(O1) 在算法运行过程中被保留下来的一组参数样本![]()
算法1的四个关键步骤为:先验分布抽样、构建数据生成器、计算统计量和计算统计量之间的距离.第一,从先验分布抽样.先验分布一般是标准分布,如正态分布、均匀分布等.因此,大多数软件包的内置函数都能轻易地从先验分布中产生样本.第二,构建数据生成器.数据生成器在不同的问题中是不同的.假设数据生成器是由一系列的常微分方程构成,那么在给定初始条件和参数值时,合成数据就可以通过数值模拟的方式产生.第三,计算统计量.如果数据存在低维度的充分统计量,那么我们就计算充分统计量.如果数据没有充分统计量,那么要计算一些概括统计量.概括统计量的选择需要研究者根据具体问题分析.第四,计算统计量之间的距离.理论上来说,我们可以计算观测数据统计量和合成数据统计量之间的任意被有效定义的距离,实际通常使用欧式距离.
算法1的操作流程将产生如下关于(θ,z)的联合分布:
(3)
其中区域Aδ定义为
Aδ={z: D(η(z),η(yn))≤δ}.
将πδ(θ,z)对z做积分,可得到关于θ的一个边缘分布如下:
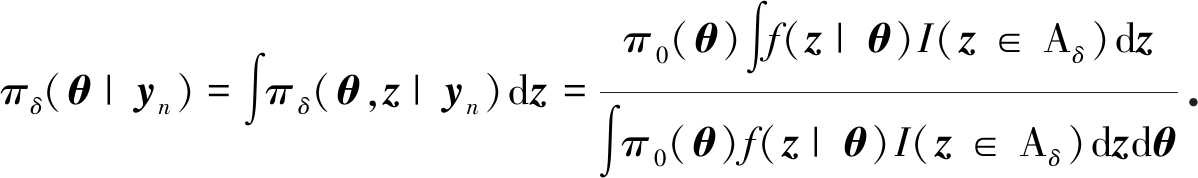
(4)
称πδ(θ|yn)为“ABC 后验分布” (ABC-posterior),并用它作为对真实后验分布π(θ|yn)的近似.如下定理为 ABC 方法给出了基本的理论保证.
定理2 如果η(yn)是yn的充分统计量且函数η(·)在yn处连续,则在一定的正则性条件下:
证明 由于η(z)是充分统计量,数据似然f(z|θ)存在如下分解:
f(z|θ)=g(η(z),θ)·h(z), ∀(z,θ).
因而
π(θ|yn)∝π0(θ)g(η(yn),θ),
(5)
(6)
定义
s(θ)=g(η(yn),θ),
并令![]() 有
有
π(θ|yn)=π0(θ)s(θ)/C,
πδ(θ|yn)=π0(θ)sδ(θ)/Cδ,
且容易验证
进而有
易知
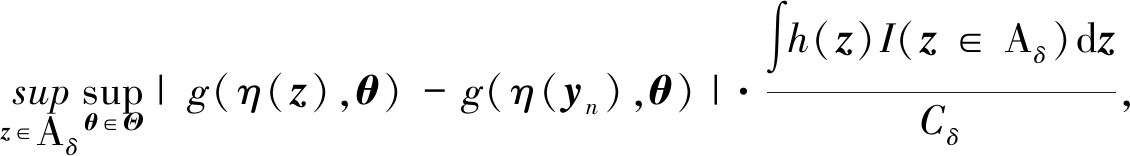
其中
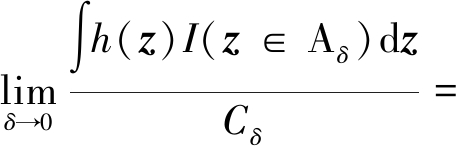
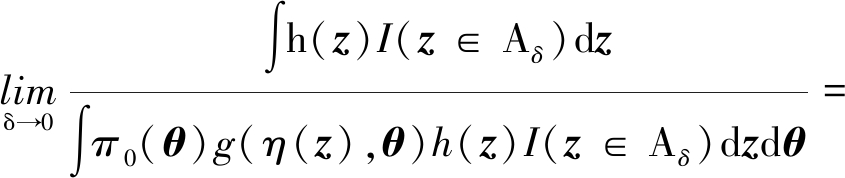
若函数g(η,θ)一致连续,则对于 >0,存在δ>0,使得
>0,存在δ>0,使得
![]()
 ,
,
即
进而,定理2得证.
□
上述定理表明:只要ABC算法中选取的统计量η是充分统计量,在一定的正则性条件下,随着距离门限值δ趋近于0, ABC后验分布πδ(θ|yn)会收敛到真实的后验分布π(θ|yn),即ABC后验对真实后验的近似误差会趋近于0.从上述定理的证明过程中还可以看到:若η不是充分统计量,则ABC后验对真实后验的近似会产生不可消除的理论误差,误差的大小取决于将数据z转化为统计量η(z)的过程中所产生的信息损失.同时,易知ABC方法中接受一个候选参数θ*的概率(即“接受率”,acceptance rate)为
显然,随着距离门限值δ趋近于0,有Cδ→0,即ABC方法的计算负担会逐渐增大直到实际的计算效率降低为0.在实际运用中,为了保持适当的计算效率,必须要选取一个非零的门限值δ,从而会不可避免地在ABC后验中引入计算误差,误差的大小取决于接受区域{z: D(η(z),η(yn))<δ}的几何特性.由于接受区域{z: D(η(z),η(yn))<δ}由统计量η、距离D和门限值δ共同决定,ABC后验分布的总误差(包括理论误差和计算误差)本质上由上述三个要素共同决定.更多关于ABC方法理论性质的讨论可以参考文献[45-46].
1.3 经典ABC方法的实际运用
由于使用了数据统计量之间相似度的比较来替代似然函数的精确计算,ABC方法放松了Bayes推断中似然函数需要有解析形式的限制条件,从而极大地扩展了Bayes推断框架的适用范围,使之可以在似然函数没有显式的解析式或者难以精确计算的情况下仍能有效运行.
早期运用ABC方法一个经典的例子是1999年Pritchard等关于群体遗传学(population genetics)的一项研究[23].在该研究中,观测到的数据集yn是一些个体的基因序列,研究目标是使用这些观测数据推断群体遗传的一些关键参数,比如基因突变率等.解决这类问题的一个常用模型是Kingman’s coalescent 模型[47],其数据似然的形式如下所示:
(7)
其中H代表在总体进化过程中未观测到的系谱历史事件集合.典型的H是一个元素个数可变、事件类型未知的高维集合.因此,上述似然函数一般而言没有显式表达式.类似的例子在传染病学[48]和生态学 [49]研究中广泛存在.
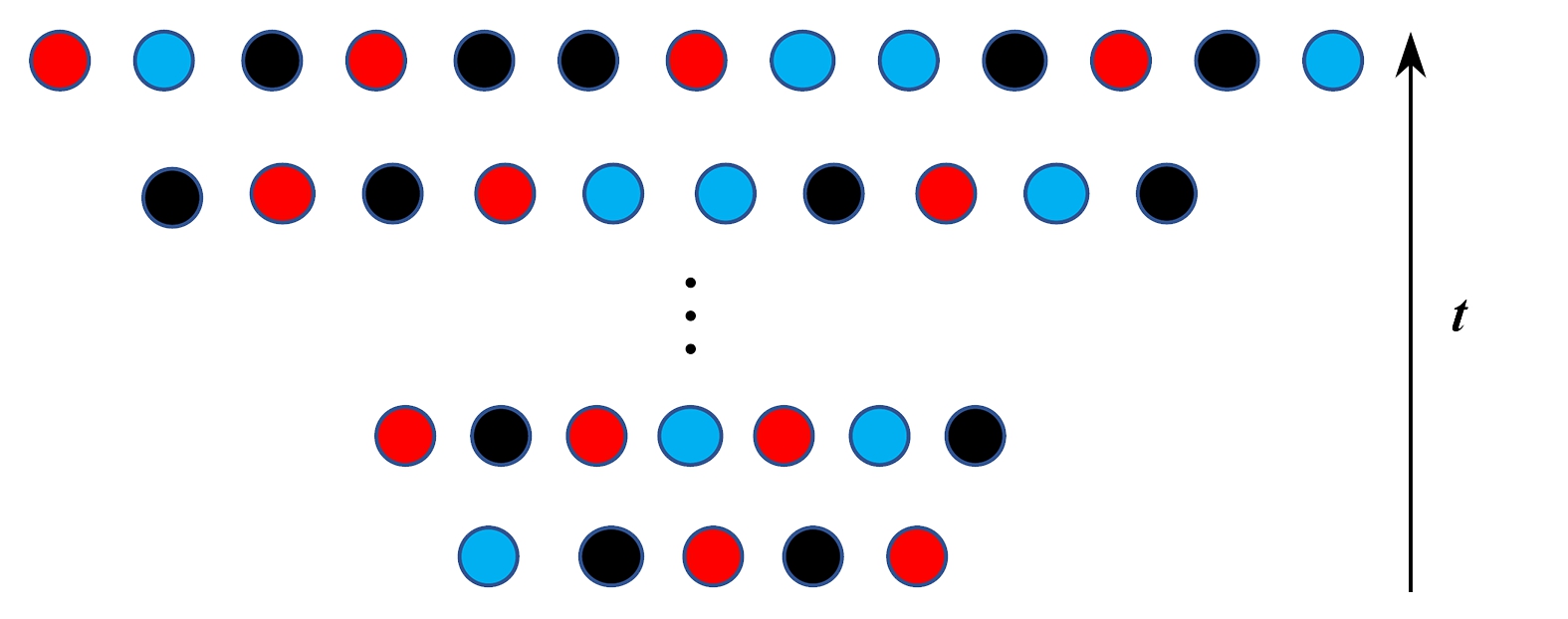
图1 总体数量变化的coalescence模型
Fig. 1 The coalescence model with population size growth
图1展示了coalescence模型,图中每行代表一个时代,不同的颜色代表不同的显型,代际之间会发生各种事件,包含死亡、生产、迁徙等,最上面一行代表当前时代的总体显型分布.虽然式(7)没有显式表达式,但是给定参数时生成这类的数据是相对容易做到的.因此,ABC方法可以处理这类问题.
另外一类有代表性的例子是空间统计中常用的Potts模型[50].图2展示了一个定义在4×4格点上的Potts模型.广义Potts模型是对分布在空间格点上的数据进行空间相关性建模的一种重要方法,在统计物理、图像处理等领域有广泛应用.给定d维空间中特定区域内的一组格点L,假设每个格点位置i对应于一个取值范围为Ω={1,2,…,q}的随机变量yi,并记y={yi}i∈L.对于格点结构中的任意两个位置i, j,如果位置i与位置j相邻,则记作i~j.Potts模型假设y具有如下形式的数据似然:
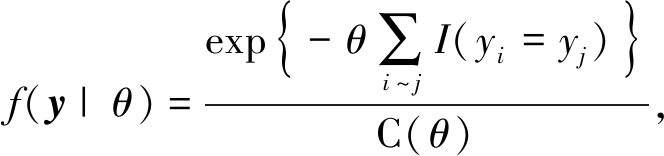
(8)
其中正则化常数C(θ)的表达式为
显然,对Potts模型数据似然的精确计算涉及到对正则常数C(θ)的计算,这需要遍历z所有可能的取值状态,其计算复杂度为O(q#L).因而,即使对于规模较小的Potts模型,其似然函数的精确计算都是非常困难的.实际上,Potts模型是Gibbs随机域(Gibbs random field,GRF)的一个特例,而几乎所有关于GRF的数据分析问题都会遇到类似的计算挑战,使运用Bayes分析面临较大的计算困难.
给定参数θ,有多种算法可以生成相应的Potts样本.同时,Potts模型的充分统计量是∑i~jI(zi =zj).这样,ABC方法可以避免计算正则化常数而对参数进行Bayes推断.
1.4 算法配置
基于前述分析, ABC后验分布的误差由统计量η、 距离D和门限值δ这三个要素共同决定.因而,在一个实际问题中运用ABC方法时,我们应在ABC方法的框架下对上述三个要素进行合理配置,以期在近似的精确性和计算的复杂性之间达到平衡,以合理的计算代价获得对真实后验分布适当的近似.从统计学一般原理上讲,统计量η应该尽可能地选取极小充分统计量(minimal sufficient statistics)为好.这是因为极小充分统计量能够在保持充分性的同时最大程度地实现对数据的压缩和降维,进而方便后续距离度量的设计和计算,从而提高算法的运行效率.然而,由于数据生成模型G(y|θ)的具体形式一般未知,确定极小充分统计量常常并不现实.这时,就需要算法的设计者根据实际问题的具体背景和专业知识来选取近似满足极小充分性的统计量.在经典ABC方法的框架下,统计量η的选取常常对整个算法的效率具有决定性的影响.在距离D的选择上,除了最常用的欧氏距离之外,还可以选择Manhattan距离、马氏距离等多种不同的距离.在不同的实际问题中,不同距离度量下的计算效率会有差异.如何选择适当的距离以达到较高的计算效率是ABC方法研究中的一个热点问题.接受域半径δ的选择是一个平衡计算成本和近似精度的过程,可以根据具体问题的应用场景和计算资源的情况进行配置.最后,我们还需要为算法设定明确的终止条件.常见的终止条件有两种:根据重复步骤(S1)~(S4)的总次数终止算法,或者根据获得的后验样本数量终止算法.但由于算法步骤(S3)中接受候选参数θ*的比率r是一个恒定的常数,这两种终止条件本质上具有等价性.
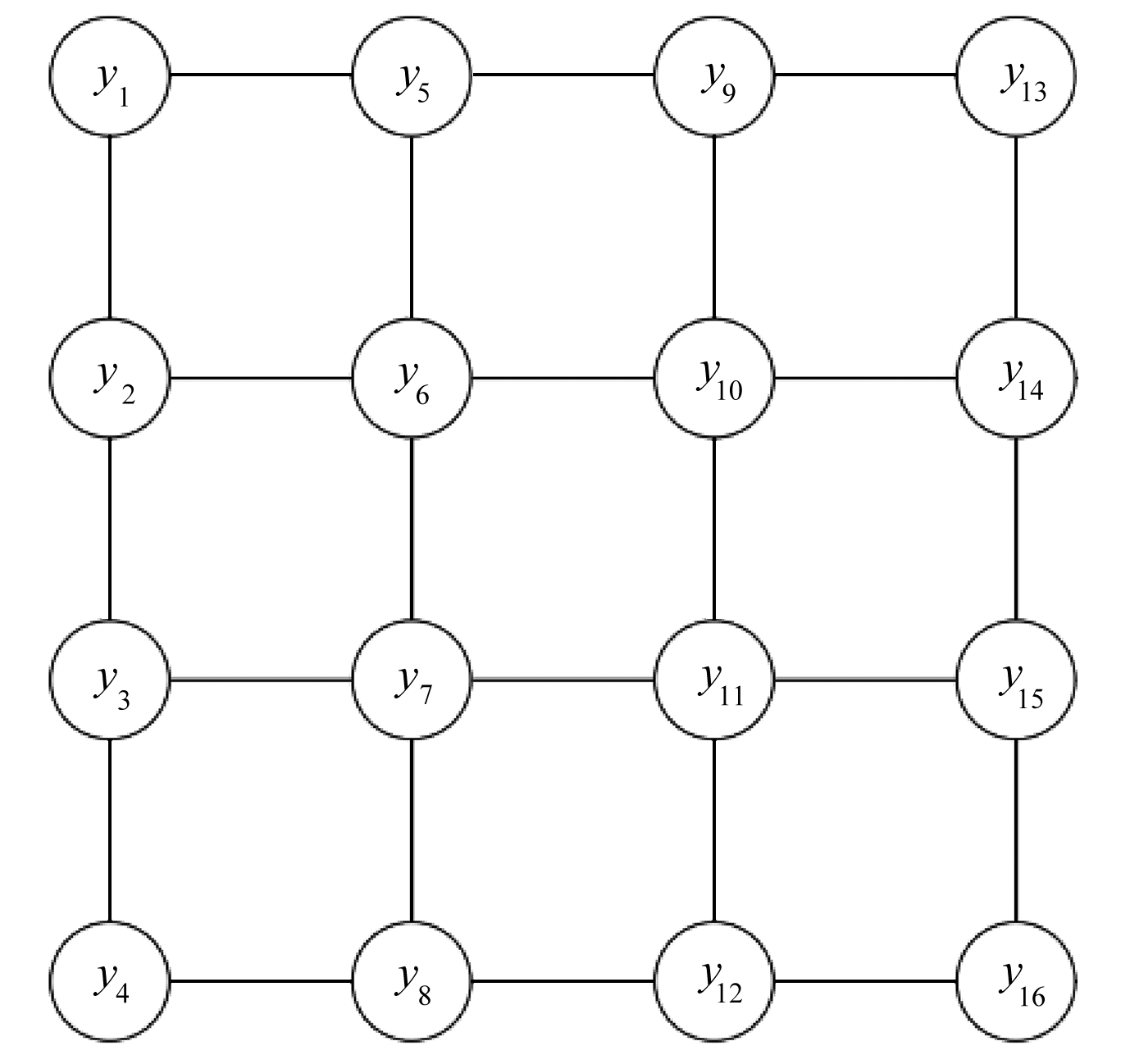
图2 定义在4×4格点上的Potts模型
Fig. 2 A Potts model defined on the 4×4 lattice
2 ABC方法前沿进展
近年来,众多研究者从不同的角度对经典ABC方法进行了改进,形成了一系列方法.本节将对这些前沿研究进展进行综述和讨论.
2.1 以数据驱动的方式筛选统计量
如前所述,选取适当的统计量是运用ABC方法的一个重要步骤.在经典的ABC框架下,统计量的选取主要依靠算法的设计者依据对实际问题的理解和经验进行人为设计.但是,在很多实际问题中,这种设计并不总是容易的.很多时候,一种统计量的选择并不显然比另一种好.而且,有研究表明统计量的不同选择会对ABC方法的实际表现产生较大的影响[51].为了克服这种困境,运用数据驱动的方式自动筛选统计量的策略近年来越来越受到重视.
Joyce和Marjoram提出一种近似充分统计量的方法[52].首先,统计量的集合S是一组试验性的统计量集合.集合S尽可能多地包含统计量. 他们认为,从S中挑选一部分统计量s就可以达到S的效果.从数学角度而言,如果π(θ| s1,s2,…,sk)/π(θ|s1,s2,…,sk-1)-1≤δ成立,sk会被认为独立于参数θ,因此sk很可能不会被纳入集合s.其中δ是研究者自定义的一个数值很小的阈值.选择s的具体方法请参考文献[52].这种方法的缺陷也很明显,对于大部分需要使用ABC的模型而言,统计量的数量并不存在一个上限.他们的研究表明,即使模型相同,当数据不同时s也会改变.
Fearnhead和Prangle提出半自动化ABC(semi-automatic ABC)来选择统计量[42].他们首先定义如下的损失函数:
(9)
其中θ为真实值,![]() 是估计值.在选择合适的矩阵A时, 当统计量s=E(θ|y)时, L会被最小化.换句话说,参数的后验分布均值是基于式(9)定义的损失函数下的最优统计量.此时,我们陷入两难的困境,因为不知道真实后验分布,后验分布的均值自然也是未知的.尽管如此,真实后验分布均值的估计量依然是可供我们选择的统计量.半自动化ABC的过程可以由算法2描述如下.
是估计值.在选择合适的矩阵A时, 当统计量s=E(θ|y)时, L会被最小化.换句话说,参数的后验分布均值是基于式(9)定义的损失函数下的最优统计量.此时,我们陷入两难的困境,因为不知道真实后验分布,后验分布的均值自然也是未知的.尽管如此,真实后验分布均值的估计量依然是可供我们选择的统计量.半自动化ABC的过程可以由算法2描述如下.
算法2 半自动化ABC算法
1) 使用算法1做试验性估计.确定参数的大致取值区间.
2) 在上述取值区间中抽取候选参数,并根据似然函数生成合成数据.重复M次该步骤,因此得到θ1,θ2,…,θM和z1,z2,…,zM.
3) 使用θ1,θ2,…,θM和z1,z2,…,zM分别估计数据和后验分布均值之间的关系.其中,第i∈{1,2,…,p}个参数θi是因变量,z是自变量.即,![]()
4) 给定统计量![]() 执行ABC算法1,得到后验样本.
执行ABC算法1,得到后验样本.
半自动化ABC算法的关键在于步骤3).Fearnhead和Prangle实验了多种方法来拟合θ与数据yn之间的关系,包括lasso[53]和canonical correlation analysis[54].他们发现, 上述方法并没有比简单线性回归表现得更好.因此, 步骤3)中使用下面的模型拟合第i个参数与数据之间的关系:
θi=β0+βf(z)+ ,
,
(10)
其中f(z)可以是z的任意组合.Fearnhead和Prangle采用f(z)=(z,z2,z3,z4).
在Fearnhead和Prangle提出半自动化ABC后,有学者扩展了步骤3)中的函数关系.Jiang等使用深度神经网络来拟合统计量与合成数据之间的关系[55].理论上来说,深度神经网络可以更好地拟合它们之间的函数关系.但是深层的神经网络需要大量的数据来学习参数.所以,Jiang等使用三隐藏层的神经网络来执行模型.使用神经网络的研究者还包括Creel[56].Raynal等提出使用随机森林的方法选择统计量[57].总体而言,目前的方法大部分集中于寻找数据与统计量之间的函数关系.这类方法比较依赖于额外的训练数据,即函数关系需要通过额外合成数据来训练得到.更多关于选择统计量的研究综述可以参考文献[58].
2.1.1 例1:“g-and-k”分位数分布(quantile ‘g-and-k’ distribution)
一元“g-and-k”分位数分布是ABC领域中常见的用于测试算法的模型[42,44].该分布由如下的形式定义:
(11)
其中, z(r)表示标准正态分布的第r个分位数, 参数c衡量分布的总体非对称性, 一般设定为0.8,需要推断的参数包括A,B,g,k.本小节对比两种算法的表现:算法1和算法2.
给定参数的真实值(A*,B*,g*,k*)=(3,1,2,0.5).数据根据真实值生成,其中样本量为n=250.因为“g-and-k”分位数分布并没有已知的充分统计量.我们使用数据的一系列分位数作为数据集的统计量.在算法中η被选定为数据的一系列分位数.其中,分位数点为[0.05,0.1,0.15,…,0.9,0.95].算法1的距离度量选择欧氏距离.对于两种算法,每种算法生成106次合成数据.算法1选择其中距离最小的N=2 048个候选参数作为其后验样本.同样地,算法2也产生N个后验样本.半自动化ABC的代码发布在R软件中的abctools包中.本文使用abctools包来实现参数推断.

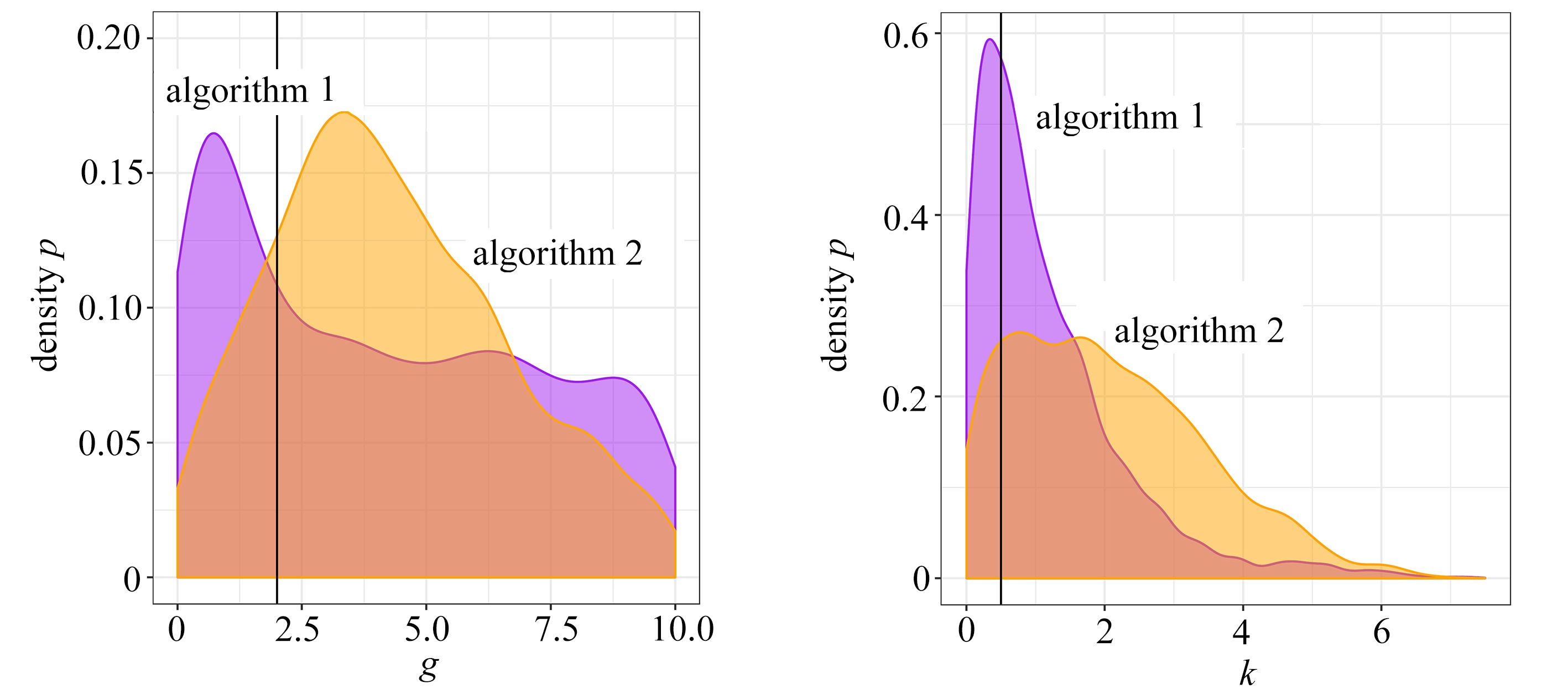
图3 对比算法1和算法2得到的参数(A,B,g,k)的后验样本边际分布
Fig. 3 Comparison of marginal distributions of (A,B,g,k) between algorithm 1 and 2
图3展示了算法1和2得到的后验样本结果,其中深色代表算法1的结果,浅色代表算法2的结果,每个子图中的黑色竖线代表每个参数的真实值.从图中可以看出,算法1在参数k的表现上是优于半自动化ABC的.在参数g上两者的表现相当,半自动化ABC略微优于算法1.在参数A,B上半自动化ABC的表现明显好过算法1.所以,总体上来看半自动化ABC表现胜过算法1,而且半自动化ABC并不需要使用者主动设计统计量.
2.2 采用更有效的距离度量
优化选取统计量之间的距离度量是改进ABC方法的另外一个重要途径.多位研究者意识到统计量的尺度差异会影响ABC的表现[45,49].Harrison等是为数不多的研究如何消除统计量之间的尺度差异影响的研究者[59],文献中以最常见的欧氏距离为例做研究.通常,经过统计量降维后,观测数据与合成数据之间的距离可以表示为
其中K是统计量的个数.为了消除统计量尺度大小的影响,Harrison等引入加权欧氏距离.其定义如下:
(12)
其中w代表统计量的权重向量.权重向量的选择会影响ABC算法得到的后验分布.文献[59]的目标就是选择最优的权重向量w*使得参数的先验分布与ABC后验分布之间的距离最大.在文献[59]中,Hellinger距离被用来衡量两个分布之间的距离.当然,其他距离度量,如欧氏距离、Kullback-Leibler散度都可以作为备选.在给定两个分布的样本时,最近邻距离估计量(nearest neighbour distance estimator)被用来估计分布之间的距离.两组样本集之间的k-最近邻距离估计的定义如下:
(13)
其中ρk(i)指Xi到它在X1:n中第k近样本的欧氏距离,νk(i)指Xi到它在Y1:n中第k近样本的欧氏距离,Bk,α=Γ(k)2/(Γ(k-α+1)Γ(k+α-1)).因此,最优的权重向量可以由最优化来解决:
(14)
其中α=0.5,θ′1:n是从先验分布中抽取的样本,θ1:n是ABC算法得到的后验分布样本.需要注意的是θ1:n与w相关.
由于观测数据的可交换性,直接使用数据集作为统计量在很多时候并不可行[58].但是最近有学者指出数据的可交换性并不会成为一个问题,并提出相应的方案实施ABC算法.比较典型的研究包括Bernton等[60]提出使用Wasserstein距离作为ABC算法中的距离度量.这样做有两个优势:首先,Wasserstein距离可以直接作用在数据集本身,它不需要统计量降维,因此就避免选择统计量的工作.第二,由Wasserstein距离诱导的ABC算法可以收敛到真实的后验分布,其原因在于数据集本身是一个充分统计量.算法3是采用Wasserstein距离的ABC算法流程,以下简称WABC.
算法3 WABC算法
1) 从先验分布θ中抽取一个候选参数θ*.
2) 给定θ*,根据真实数据生成过程产生一个合成数据z.
3) 计算W(z,y),其中W(·,·)代表Wasserstein距离.
4) 如果W(z,y)≤δ,保留θ*和z.
5) 重复步骤1)~4),直到算法的终止条件被满足.
2.2.1 例2:回访“g-and-k”分位数分布
我们回访在第2.1.1小节中的例子,使用算法3对观测数据做参数推断.算法3的代码可以在github.com/pierrejacob/winference找到.为了寻找一个合理的阈值 ,WABC与序列Monte-Carlo方法结合.关于序列Monte-Carlo的介绍,可以参考本文第2.3.2小节.
,WABC与序列Monte-Carlo方法结合.关于序列Monte-Carlo的介绍,可以参考本文第2.3.2小节.
图4展示了算法2和算法3得到的后验样本的边际分布情况,其中深色代表算法3的结果,浅色代表算法2的结果,每个子图中的黑色竖线代表每个参数的真实值.很显然,使用Wasserstein距离的ABC算法明显优于半自动化ABC.在每个参数的边际分布上,算法3都是更优的.不仅如此,WABC还极大地简化了使用ABC算法的过程.使用者不需要设计统计量来降低数据的维度.但是WABC遇到的另一个问题是Wasserstein距离的计算复杂度高.如果观测样本的样本量为n且样本是多元数据,那么精确Wasserstein距离的计算复杂度为O(n3).在文献[60]中,研究者提供了关于近似求解Wasserstein距离的一些方法.它们都可以降低计算成本,但是需要牺牲一部分计算精度.
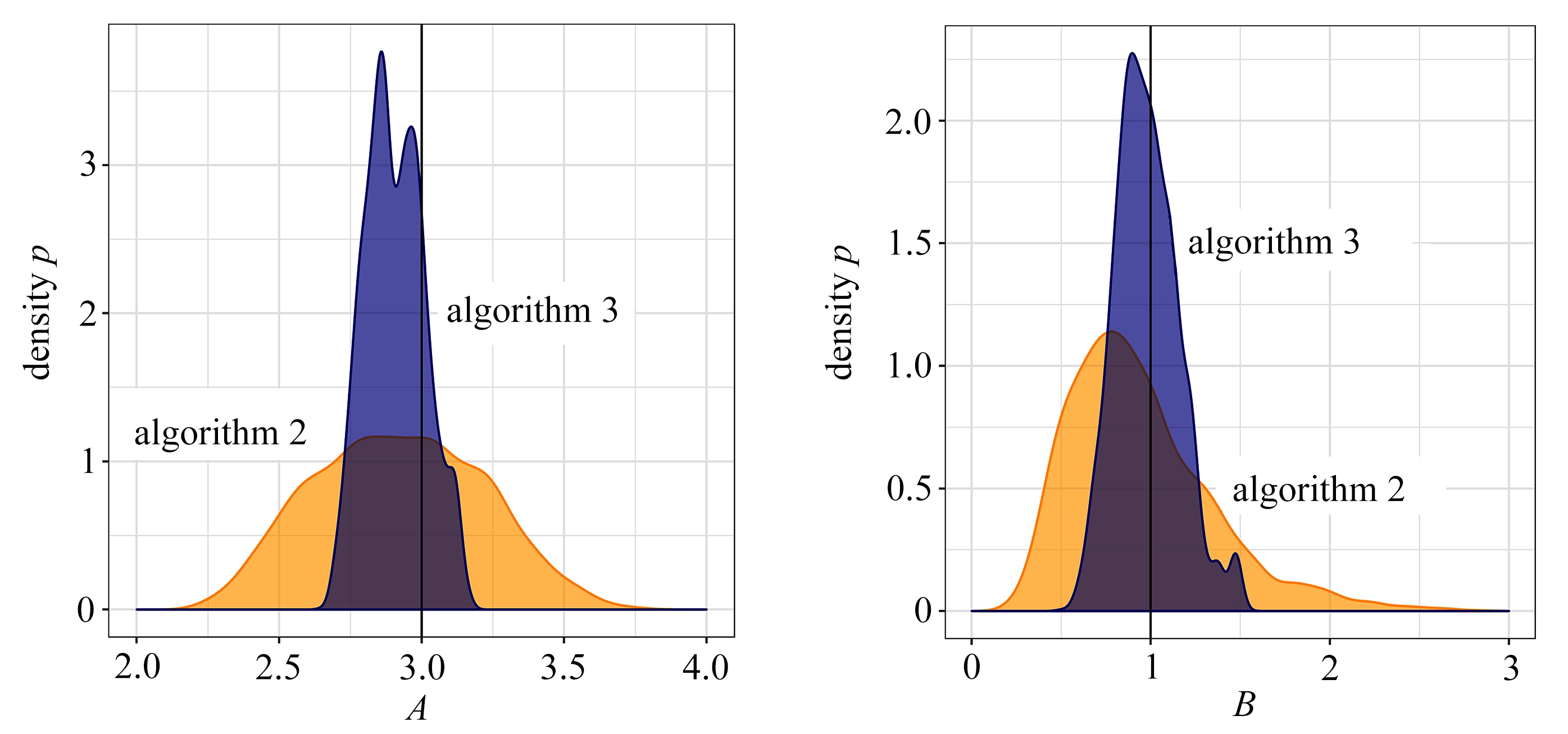
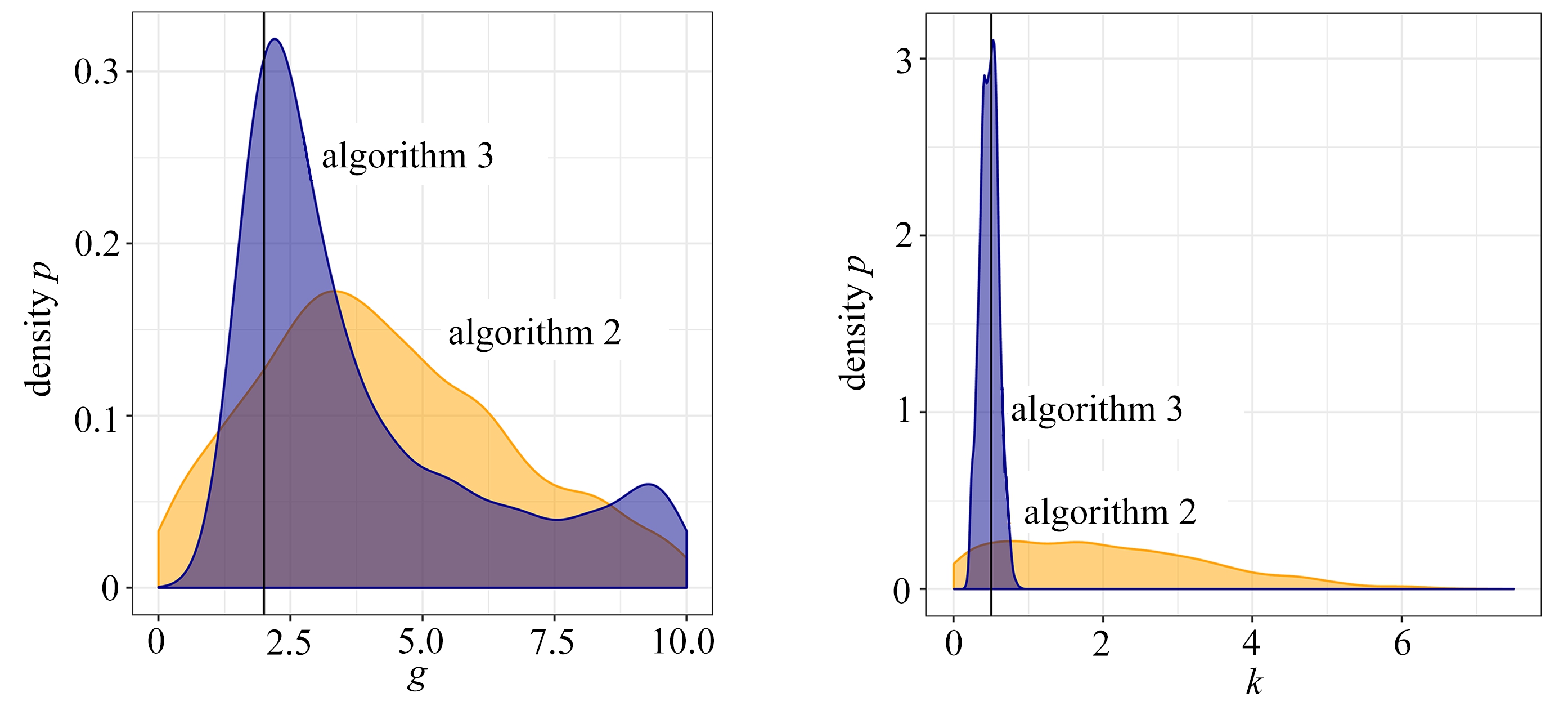
图4 对比算法2和算法3得到的参数(A,B,g,k)的后验样本边际分布
Fig. 4 Comparison of marginal distributions of (A,B,g,k) between algorithm 2 and 3
2.3 计算框架的进一步扩展
实际上,经典ABC算法框架的计算效率是比较低的.为了提高ABC算法的计算效率,学者们对经典ABC算法的计算框架进行了一系列扩展和改进,将ABC方法与其他的抽样和分析技术进行有效整合以提高计算效率.
2.3.1 Soft ABC
算法1使用拒绝和接受两种极端的方式对待候选参数.这种方式被称为“拒绝抽样ABC”.与之对应的是soft ABC,其具体流程如算法4所示.
算法4 Soft ABC算法
1) 从先验分布π(θ)中抽取一个候选参数θ*.
2) 给定θ*,根据真实数据生成过程产生一个合成数据z.
3) 计算相似度r=exp(-D(z,yn)/h),其中D(·,·)代表某种距离度量(如,欧氏距离).
4) 依概率r保留θ*和z.
5) 重复步骤1)~4),直到算法的终止条件被满足.
显然,算法4中h的作用与算法1中的δ类似,控制了soft ABC方法的近似精度和计算效率.当h→0时,soft ABC方法的近似精度逐渐提高,但计算效率逐渐降低.在实际应用soft ABC的过程中,我们需要适当地选择h.
在此基础上,Park等在2016年提出可以用两个样本之间的最大均值差异(maximum mean discrepancy,MMD)替代其距离度量D,对soft ABC方法进行改造.该算法被简称为K2-ABC[61],其具体流程如算法5所示.
算法5 K2-ABC算法
1) 从先验分布π(θ)中抽取一个候选参数θ*.
2) 给定θ*,根据真实数据生成过程产生一个合成数据z.
3) 计算相似度δ=exp(-DMMD(z,yn)/h),其中DMMD表示距离.
4) 依概率δ保留θ*和z.
5) 重复步骤1)~4),直到算法的终止条件被满足.
2.3.2 ABC-SMC
经典ABC框架的一大局限在于:候选参数是从参数的先验分布抽取的,当先验分布与后验分布差异较大时,一般会造成很高的抽样拒绝率.这一弊端可以通过巧妙地构造更加接近于后验分布的抽样分布来部分克服.ABC-SMC算法[41,62]对经典ABC框架中产生候选参数的抽样过程进行了改造,通过序列Monte-Carlo策略逐步优化更新候选参数的抽样分布.ABC-SMC算法由T+1个串行的ABC过程所构成,每一个ABC过程对应于一个不同的阈值δt,其中∞=δ0 >δ1>…>δT.其详细流程如算法6所示.
算法6 ABC-SMC算法
1) 令t=0.从先验分布π0(θ)中抽取N个样本![]() 并对每个样本赋予权重
并对每个样本赋予权重![]()
2) 令t=t+1.构造混合分布![]() 其中K(·|·)是给定的转移核函数.
其中K(·|·)是给定的转移核函数.
3) 令i=1.
4) 以混合分布G(t)(θ)为抽样分布,以δt为门限值,运行ABC算法获得关于参数θ的新样本:首先从G(t)(θ)中抽样得到![]() 进而从数据生成器生成合成数据
进而从数据生成器生成合成数据![]() 并重复该步骤直到D(η(yn),η(z))≤δt.
并重复该步骤直到D(η(yn),η(z))≤δt.
5) 令i=i+1.返回步骤4),直至i>N.
6) 赋予样本权重:
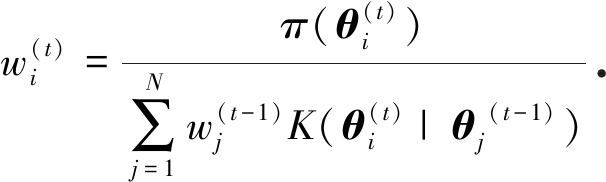
7) 返回步骤2),直至t>T.
在算法6中转移核函数K(·|·)通常可以选择Gauss核函数.由于在t时刻,候选参数不再是从先验分布π0(θ)抽取,而是从以t-1时刻获得的样本为局部中心所形成的Gauss混合分布G(t)(θ)抽取,ABC-SMC算法可以有效继承我们在t时刻之前对后验分布的近似认知,从而提高算法的抽样效率.在ABC中使用SMC方法的研究还包括文献[63-64].
2.3.3 ABC-MCMC
Marjoram等提出了在ABC框架中使用MCMC的方法以提高计算效率[40].具体算法流程如算法7所示.在算法7中,似然函数不需要被计算.同时,当δ→0时,算法得到的后验分布收敛到真实的后验分布.ABC-MCMC的优势在于,候选参数不需要从先验分布获得.通常K(·|·)选择Gauss核函数.如果K(·|·)和参数的先验分布都选择均匀分布,那么ABC-MCMC就会退化为算法1.如果目标分布是多峰分布,ABC-MCMC面临的挑战是后验样本容易陷入局部单峰区间.
算法7 ABC-MCMC算法
1) 令t=0.使用算法1得到一个后验样本θ(0).
2) 令t=t+1.
3) 抽样候选参数θ*~K(·|θ(t-1)).
4) 给定θ*,根据真实数据生成过程产生一个合成数据z.
5) 生成随机数u~U(0,1).
6) 计算![]()
7) 如果u≤r和D(η(yn),η(z))≤δ都成立,则令θ(t)=θ*,z(t)=z.否则,θ(t)=θ(t-1). 8) 返回步骤2),直到算法的终止条件被满足.
2.3.4 Hamiltonian ABC
Hamiltonian Monte-Carlo(HMC)方法是一种常见的处理高维推断的方法[65].HMC利用目标函数的一些信息(如,梯度信息和Hesse矩阵等)来提高参数的抽样效率.但是ABC不需要任何密度函数的信息.直觉上来说,HMC与ABC是两种思路相反的框架.但是Meeds等将两种方法结合[66],这种方法被简称为HABC.HABC可以同时拥有HMC和ABC的优势:处理高维参数推断和免于计算似然函数.
面对复杂模型,似然函数难以计算.HMC缺少似然函数的信息就不能进行抽样.但是ABC得到的后验样本却可以帮助我们了解似然函数的大致信息.在HABC中一个关键的公式是
(15)
其中z(1),z(2),…,z(M)是由ABC算法获得的M个后验样本,π (yn|z)表示合成数据与观测数据之间的差异,也可以当作似然函数.因此,对于给定的θ,观测数据的似然函数都可以根据式(15)计算.相应地, 观测数据似然函数的梯度信息都可以近似地计算.因此, HMC可以顺利实施.
(yn|z)表示合成数据与观测数据之间的差异,也可以当作似然函数.因此,对于给定的θ,观测数据的似然函数都可以根据式(15)计算.相应地, 观测数据似然函数的梯度信息都可以近似地计算.因此, HMC可以顺利实施.
令H(θ,p)=U(θ)+ K(p)代表Hamilton动力系统的能量方程,其中θ是待估参数,p是动量向量.算法8给出了HABC算法的流程.
算法8 HABC算法
1) 令t=0.从先验分布中产生初始参数θ(0).
2) 令t=t+1.
3) 抽样初始动量参数p(t-1)~π0(p).
4) 执行L步蛙跳算法(leap-frog),起点为[θ(t-1),p(t-1)],步长为δLF.最终得到θ*,p*.
5) 计算r=min(1,exp(-U(θ*)+U(θ(t-1))-K(p*)+K(p(t-1)))).
6) 令u代表标准均匀分布的一个随机数.如果u ≤r,则令θ(t)=θ*.否则,θ(t)=θ(t-1).
7) 返回步骤2),直到算法的终止条件被满足.
步骤4)中的蛙跳算法具体实施如下:
其中∂U/∂θi(t)可以根据式(15)得到.
ln M +ln δ+(yn-z(m*))2/(2δ2),
其中z(m*)是距离观测数据最近的合成数据.
2.3.5 合成似然函数
合成似然函数(synthetic likelihood)方法是与ABC算法相近的算法之一.合成似然函数是由文献[49]提出.他的目标是对复杂的非线性模型做统计推断.由于观测数据具有高度的非线性和模型的复杂性,似然函数难以计算.他提出将观测数据yn转化为一系列的统计量s.之后所有的统计推断都是基于统计量的空间进行.
在给定参数θ时,通过生成大量合成数据z1:N,计算相应的统计量![]() 他假定统计量服从多元Gauss分布,即sθ~N(μθ,Σθ).所以,借助
他假定统计量服从多元Gauss分布,即sθ~N(μθ,Σθ).所以,借助![]() 估计μθ, Σθ.因此,对于特定的θ,观测数据的似然函数是可以计算的.令θobs代表观测数据的相应统计
估计μθ, Σθ.因此,对于特定的θ,观测数据的似然函数是可以计算的.令θobs代表观测数据的相应统计![]() 其中φ(·|θ)是多元正态分布的密度函数. 因此,MCMC可以用于从合成似然函数中获得后验样本.
其中φ(·|θ)是多元正态分布的密度函数. 因此,MCMC可以用于从合成似然函数中获得后验样本.
合成似然函数与ABC的相同之处在于:它们都需要生成大量的合成数据.不同之处在于:合成似然函数假设合成数据的统计量服从特定的分布,而ABC则直接比较生成数据与观测数据之间的差异.显然合成似然函数并不是真正的似然函数.它使用一个易于计算的似然函数代替了难以计算的真正似然函数.本质上,ABC方法不需要计算似然函数,但是合成似然函数方法是基于似然函数的推断方法.
3 ABC方法在复杂数据处理中的应用
ABC方法的上述前沿进展在一系列复杂数据处理问题中有着广泛的应用,并和对抗生成网络等前沿人工智能方法有着深刻的内在联系.本节将对相关案例和联系给予讨论.
3.1 ABC方法与连续时间自回归
在信号处理、金融等领域经常会处理连续时间序列的数据类型.连续时间自回归模型(continuous-time autoregressive model,CAR )是处理这类数据的常用模型.经典CAR模型可以使用Kalman滤波(Kalman filtering)和粒子滤波(particle filter)做统计推断[67].然而,一旦CAR模型中的一些经典假设条件不再成立,其统计推断就会遇到很大的挑战.ABC方法是解决这类挑战的一个有力工具[68].
通常,在状态空间形式下,P阶CAR模型被如下描述:
(16)
其中,{W(t)}是标准Brown运动,X(t)=[X(t), X(1)(t), …, X(P-1)(t)]T(X(i)(t)表示X(t)的第i阶导数),

(17)
![]() 模型的It
模型的It 积分解如下[69-70]:
积分解如下[69-70]:
(18)
其中状态转移是Gauss密度函数:
f(X(t)|X(s))=N(eAtX(s),C(t,s)), s<t,
(19)
(20)
连续时间过程可以放在如下离散状态空间:
Xti=eA(ti-ti-1)Xti-1+eti, i=1,2,…,N,
(21)
其中系统噪声![]() 它的方差是
它的方差是
(22)
如果驱动噪声{W(t)}是标准Brown运动,那么Kalman滤波方法可以精确求解似然函数[68].但是,在{W(t)}不满足标准Brown运动的假设时,计算似然函数就尤其困难.我们考虑一阶CAR模型.令![]() 观测数据为X=(Xt1,Xt2,…,XtN).我们观察到,给定一组参数候选值θ*,可以根据式(21)计算zti=Xti-eA*(ti-ti-1)Xti-1.如果θ*与真实值一致且t1,t2,…,tN是等差数列,那么序列zti是独立同分布的的样本集.因此,可以根据zti是否为独立同分布来推测θ*与真实值的差异度.近年来,距离相关性(distance correlation)[71]是双样本检测的一个热门工具.我们拟使用距离相关性与ABC结合的方法推断CAR模型的参数.算法由文献[68]提出,具体的步骤由算法9展示.
观测数据为X=(Xt1,Xt2,…,XtN).我们观察到,给定一组参数候选值θ*,可以根据式(21)计算zti=Xti-eA*(ti-ti-1)Xti-1.如果θ*与真实值一致且t1,t2,…,tN是等差数列,那么序列zti是独立同分布的的样本集.因此,可以根据zti是否为独立同分布来推测θ*与真实值的差异度.近年来,距离相关性(distance correlation)[71]是双样本检测的一个热门工具.我们拟使用距离相关性与ABC结合的方法推断CAR模型的参数.算法由文献[68]提出,具体的步骤由算法9展示.
算法9 针对CAR模型的ABCDC算法
1) 令0时刻观测值为X(0)=x.
2) 从先验分布π(a)中抽样一组候选值a*.
3) 如果P=1, 进入步骤4). 否则,使用数值方法获得X(t)的导数.
4) 计算zti=Xti-eA(ti-ti-1)Xti-1.
5) 将{z}划分为两部分.令z1={z1,z3,…}以及z2={z2,z4,…}.
6) 计算距离相关性Dcor(z1,z2).
7) 如果Dcor(z1,z2)≤ε,接受a*.
8) 返回步骤2),直至终止条件达成.
为了提高抽样效率,在实际应用中可以将上述算法与MCMC结合,形成ABCDC-MCMC算法.此处不再赘述算法细节,有兴趣的读者可以参考文献[68].相关方法的实际效果得到了数值模拟的验证.
Ornstein Uhlenbeck(OU)过程是连续时间序列模型的一类过程.不同的驱动过程定义不同的OU过程.图5(a)给出了从如下OU过程中产生的一组模拟数据:
Xti=ea(ti-ti-1)Xti-1+Wti, i=1,2,…,N,
(23)
其中,Wti=σe![]() ea(ti-u)dL(u),L代表驱动过程,参数的真值为a=-0.8,σe=1.此处,令L表示Brown运动.
ea(ti-u)dL(u),L代表驱动过程,参数的真值为a=-0.8,σe=1.此处,令L表示Brown运动.
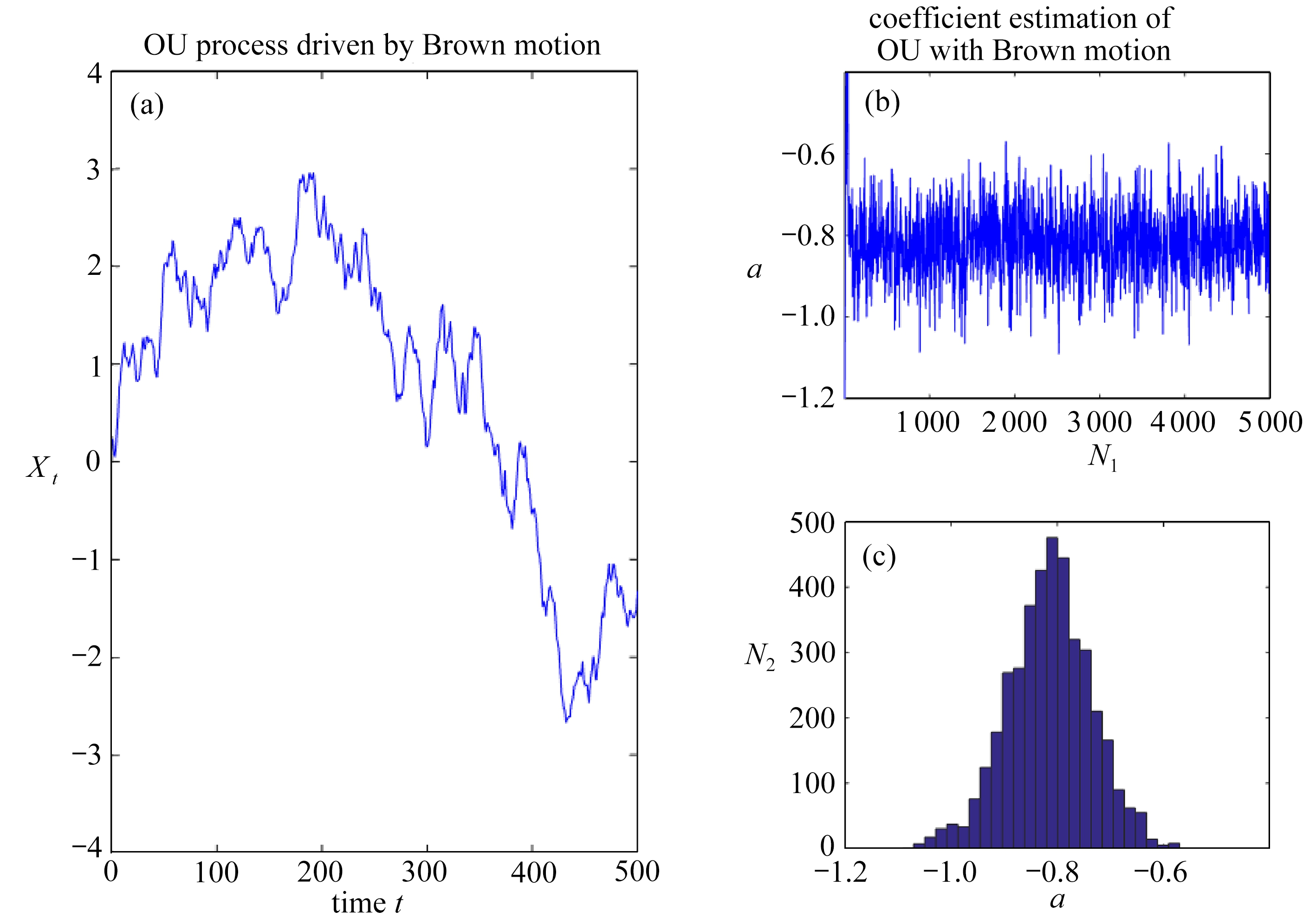
图5 连续时间自回归模型的Bayes推断
Fig. 5 Bayesian inference of coutinuous-time autoregression model
图5(b)、(c)展示了运用 ABCDC-MCMC算法所得到关于参数a的近似后验分布,其中图5(b)为参数a的MCMC样本,图5(c)为参数a的直方图.相关结果表明ABCDC-MCMC方法能够有效推断参数a.而Wti的方差为![]() 因此,令
因此,令![]() 代表a的估计值,则
代表a的估计值,则

3.2 ABC方法与人工智能
以生成对抗网络(GAN)和变分自动编码器(VAE)为代表的新型生成模型是近年来人工智能研究中的一大热点,其应用范围涵盖了图像、语音、文本等常见的复杂数据应用领域.给定一组希望被模仿的目标数据样本,这类方法力图输出一组生成数据样本,使得生成数据样本与目标数据样本尽可能相似而不能被区分.不同于在应用数学和统计学中广泛使用的基于领域知识进行建模的传统生成模型,这些新型生成模型以数据驱动的方式,通过人工模拟的手段,对数据生成过程进行探索和刻画.作为对生成模型进行统计推断的一般性方法,ABC方法原则上可以与GAN和VAE深度结合,在人工智能研究中引入不确定推断的理念和方法,并运用前沿人工智能技术推动不确定性推断方法的不断发展.
一般而言,GAN由一个生成网络(generative network)和一个判别网络(discriminative network)构成,其中生成网络用于产生生成数据样本,判别网络用于区分生成数据样本和目标数据样本.GAN方法的核心在于:通过生成网络和判别网络之间迭代进行的对抗训练来不断提高两者的能力,并最终使得生成网络输出的生成数据样本达到可以乱真的程度.所谓的对抗训练一般由两个步骤组成:首先,训练生成网络,使得其生成的样本可以骗过当前的判别网络,被判别为和目标数据样本属于同一类别;然后,训练并更新判别网络,使其能够以更大的概率正确区分生成样本和目标样本.容易看到,通过迭代式的对抗训练,生成网络和判别网络的能力均可不断提升,并最终到达某种平衡.令G表示所有可容许的生成网络所构成的空间,D表示所有可容许的判别网络所构成的空间,上述通过迭代对抗训练来改进直观生成及判别网络的过程可以通过求解如下优化问题来实现[9]:
其中目标函数:
V(G,D) Ey~pdata(y)[ln(D(y))]+Ez~pz(z) [ln(1-D(G(z)))],
Ey~pdata(y)[ln(D(y))]+Ez~pz(z) [ln(1-D(G(z)))],
(24)
其中pdata(y)代表观测数据的真实分布,pz(z)代表生成网络输入的分布.有进一步的理论研究发现:上述优化问题等效于最小化由生成网络产生的生成数据样本的概率分布FG与目标数据所对应的概率分布FT之间的KL散度[9].考虑到当FG与FT的支持空间重叠度较小或无重叠的时候,这种基于KL散度的优化策略常常无法提供可引导优化算法的有效信号(即所谓“梯度消失”现象),从而造成对抗训练的失败,人们开始尝试使用一系列基于双样本检测(two sample test)的统计量(包括Wasserstein 距离[16]、最大平均差异[72]、能量距离和χ2距离[19]等)来替代KL散度作为度量生成数据样本与目标数据样本相似程度的度量.相关改进产生了一系列效果非常好的新型GAN算法,在一系列应用问题中取得了显著的效果.
作为生成模型的另一种典型代表,VAE[10]由一个编码器(encoder)和一个解码器(decoder)构成.其中,编码器将输入的目标数据样本转换为近似服从d-维标准正态分布Nd的一组隐变量{Hi![]() ,并用这些隐变量及其分布Nd表示目标数据样本的核心特征;然后,通过从分布Nd中抽取新的隐变量H*并透过解码器对H*进行解码即可产生一个新的生成数据样本y*.事实上,变分自动编码器是“变分法”(variational Bayesian)的一项重要应用.变分法是针对大规模模型和海量数据的Bayes推断算法的改进.特别是随机变分法(stochastic variational inference)的提出[73],它放弃了推导解析变分公式的复杂过程,改用随机梯度下降(stochastic gradient descent, SGD)算法求解变分分布,使得这类变分法特别适合解决大规模Bayes模型.
,并用这些隐变量及其分布Nd表示目标数据样本的核心特征;然后,通过从分布Nd中抽取新的隐变量H*并透过解码器对H*进行解码即可产生一个新的生成数据样本y*.事实上,变分自动编码器是“变分法”(variational Bayesian)的一项重要应用.变分法是针对大规模模型和海量数据的Bayes推断算法的改进.特别是随机变分法(stochastic variational inference)的提出[73],它放弃了推导解析变分公式的复杂过程,改用随机梯度下降(stochastic gradient descent, SGD)算法求解变分分布,使得这类变分法特别适合解决大规模Bayes模型.
受GAN和ABC算法的影响,近期VAE模型也在尝试用统计量的度量做似然函数的近似,如文献[74]用MMD等统计量替代VAE中的分布解析表达式;如文献[75]提出对抗自动编码器,将VAE的变分推断与GAN中判别网络的统计量度量结合在一起.此外,变分法的发展,也给ABC的Bayes推断过程提供了新的思路.文献[76]提出了变分ABC,用变分推断替代传统ABC中基于Monte-Carlo抽样的后验分布估计.也可以说是用统计量度量替代传统变分推断中的似然函数,为变分推断和ABC算法的融合做出了典范.
其实从某种意义上来说,GAN及其变种模型属于泛化的ABC算法.它们使用深度神经网络作为样本数据生成器,然后使用深度神经网络作为判别器.此处判别网络先将数据变换到一个较低维度的特征向量,然后用生成样本的特征向量与目标样本的特征向量之间的距离作为度量,并以此度量来设计损失函数.与ABC不同的之处有二:第一,GAN模型泛化了ABC方法的数据生成方式,ABC方法的数据生成方式是已知的,GAN模型需要学习数据的生成方式.第二,经典的ABC模型需要使用者提供数据的统计量,GAN方法是通过判别网络学习数据的特征向量.可以预见ABC领域的理论发展,特别是构建高维数据的统计量、统计量的度量和判别等方面的进步,将进一步促进GAN网络等生成模型的进步;同时GAN网络等新兴生成模型的进步,也给ABC在大规模、复杂数据领域的应用提供了新的思路.
以上关于GAN和VAE的模型大多数只注重得到模型的“最优解”.在众多场景下,如医疗[77]、自动驾驶(对结果判断可靠性要求比较高)“最优解”往往并不足够.然而,不确定性推断可以帮助获得关于参数的更全面信息.ABC算法可以对模型的不确定性进行量化分析,使模型给出更加安全可靠的推断.可以预见ABC中用样本统计量替代解析似然函数的哲学理念,融合了深度神经网络的复杂而灵活的统计模型和基于变分法的大规模Bayes推断算法三者的相互融合,将成为人工智能领域研究的热点,也会使得ABC类型的算法在机器学习领域获取更大的应用空间.另外,ABC领域的理论发展,特别是构建高维数据的统计量、统计量的度量和判别等方面的进步,将进一步促进GAN网络等生成模型的进步;同时GAN网络等新兴生成模型的进步,也给ABC在大规模、复杂数据领域的应用提供了新的思路.
4 结 论
生成模型能够有效处理复杂数据的模型和算法以从数据中获取有用的信息和知识.它已经成为机器学习和统计学习中的重要研究领域.虽然生成模型在大数据时代拥有巨大的优势,但是目前的生成模型并不重视不确定性分析.近似Bayes计算既拥有生成模型的优势,又能实现不确定性分析.因此,本文期望能够将近似Bayes计算的优势与深度学习技术结合,发展出更加完善的生成模型算法,以期它能够在大数据时代发挥作用.首先,本文回顾了ABC的产生和发展历程.其次,对于ABC与其他技术的关系和扩展也做了比较详细的描述.ABC的发展主要集中在三个方面:构建统计量、选择距离度量和选择阈值.这三个方面制约了ABC的应用也在推动ABC的发展.然后,我们介绍了ABC技术在大数据时代的应用潜力.
总体而言,ABC框架已经成为统计计算和统计学习领域的一个重要分支.在统计领域,它可以处理复杂模型,如生态模型、生物模型和传染病模型等.在当今的大数据时代,模型变得更加复杂,基于似然函数的方法遇到很大挑战.ABC与其他大数据技术逐渐结合,它们在处理复杂数据和模型时拥有巨大优势,相信ABC会在大数据时代发挥更加重要的作用.
致谢 本文作者衷心感谢北京智源人工智能研究院对本文的支持.
[1] STRANG G. Introduction to Applied Mathematics[M]. Wellesley, MA: Wellesley-Cambridge Press, 1986.
[2] 谷超豪, 李大潜, 陈恕行. 数学物理方法[M]. 上海: 上海科学技术出版社, 2002.(GU Chaohao, LI Daqian, CHEN Shuxing. Mathematical and Physical Methods[M]. Shanghai: Shanghai Scientific & Technical Publishers, 2002.(in Chinese))
[3] BOARD A. Stochastic Modelling and Applied Probability[M]. Springer, 2005.
[4] COURANT R, HILBERT D. Methods of Mathematical Physics: Partial Differential Equations[M]. John Wiley & Sons, 2008.
[5] ARNOL’D V I. Mathematical Methods of Classical Mechanics[M]. Springer Science & Business Media, 2013.
[6] NETER J, KUTNER M H, NACHTSHEIM C J, et al. Applied Linear Statistical Models[M]. Chicago, 1996.
[7] CONGDON P. Bayesian Statistical Modelling[M]. John Wiley & Sons, 2007.
[8] FAHRMEIR L, TUTZ G. Multivariate Statistical Modelling Based on Generalized Linearmodels[M]. Springer Science & Business Media, 2013.
[9] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Advances in Neural Information Processing Systems 27 (NIPS 2014). Montreal, Canada, 2014.
[10] KINGMA D P, WELLING M. Auto-encoding variational Bayes[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1511.06434.pdf.
[11] RADFORD A, METZ L, CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1312.6114.pdf.
[12] CHEN X, DUAN Y, HOUTHOOFT R, et al. Infogan: interpretable representation learning by information maximizing generative adversarial nets[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1606.03657.pdf.
[13] ZHANG Han, XU Tao, LI Hongsheng, et al. Stackgan: text to photo-realistic image synthesis with stacked generative adversarial networks[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1612.03242v1.pdf.
[14] MAO X D, LI Q, XIE H R, et al. Least squares generative adversarial networks[C]//2017 IEEE International Conference on Computer Vision (ICCV). 2017.
[15] ISOLA P, ZHU J Y, ZHOU T H, et al. Image-to-image translation with conditional adversarial networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). 2017: 1125-1134.
[16] ARJOVSKY M, CHINTALA S, BOTTOU L. Wasserstein GAN[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1701.07875.pdf.
[17] ZHU J Y, PARK T, ISOLA P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]//2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy, 2017.
[18] KARRAS T, LAINE S, AILA T. A style-based generator architecture for generative adversarial networks[C]//2019 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). 2019: 4401-4410.
[19] TAO C Y, CHEN L Q, HENAO R, et al. Chi-square generative adversarial network[C]//International Conference on Machine Learning. 2018: 4894-4903.
[20] SØNDERBY C K, RAIKO T, MAALØE L, et al. Ladder variational autoencoders[C]//Advances in Neural Information Processing Systems 29 (NIPS 2016). 2016: 3738-3746.
[21] HIGGINS I, MATTHEY L, GLOROT X, et al. Early visual concept learning with unsupervised deep learning[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1606.05579.pdf.
[22] RUBIN D B. Bayesianly justifiable and relevant frequency calculations for the applies statistician[J]. The Annals of Statistics, 1984, 12(4): 1151-1172.
[23] PRITCHARD J K, SEIELSTAD M T, PEREZ-LEZAUN A, et al. Population growth of human Y chromosomes: a study of Y chromosome microsatellites[J]. Molecular Biology & Evolution, 1999, 16(12): 1791-1798.
[24] WILKINSON R D,TAVARÉB S. Estimating primate divergence times by using conditioned birth-and-death processes[J]. Theoretical Population Biology, 2009, 75(4): 278-285.
[25] PETERS G W, SISSON S A, FAN Y. Likelihood-free Bayesian inference for Alpha-stable models[J]. Computational Statistics & Data Analysis, 2012, 56(11): 3743-3756.
[26] NOTT D J, FAN Y, MARSHALL L, et al. Approximate Bayesian computation and Bayes’ linear analysis: toward high-dimensional ABC[J]. Journal of Computational and Graphical Statistics, 2014, 23(1): 65-86.
[27] RATMANN O, ANDRIEU C, WIUF C,et al. Model criticism based on likelihood-free inference, with an application to protein network evolution[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(26): 10576-10581.
[28] KULKARNI T, YILDIRIM I, KOHLI P,et al. Deep generative vision as approximate Bayesian computation[C]//NIPS 2014 ABC Workshop. 2014.
[29] SHEEHAN S, SONG Y S. Deep learning for population genetic inference[J]. PLoS Computational Biology, 2016, 12(3): e1004845. DOI: 10.1371/journal.pcbi.1004845.
[30] GAL Y, GHAHRAMANI Z B. Dropout as a Bayesian approximation: representing model uncertainty in deep learning[C]//Proceedings of the 33rd International Conference on Machine Learning. New York, USA, 2016: 1050-1059.
[31] FELIP J, AHUJA N, GOMEZ-GUTIERREZ D, et al. Real-time approximate Bayesian computation for scene understanding[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1905.13307.pdf.
[32] GHOSH J K, RAMAMOORTHI R V. Bayesian Nonparametrics[M]. New York: Springer, 2003.
[33] ROBERT C.The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation[M]. Springer Science, 2007.
[34] BERNARDO J M, SMITH A F M. Bayesian Theory[M]. John Wiley & Sons, 2009.
[35] GELMAN A, CARLIN J B, STERN H S, et al. Bayesian Data Analysis[M]. 3rd ed. Chapman and Hall/CRC, 2013.
[36] LIU J S. Monte Carlo Strategies in Scientific Computing[M]. New York: Springer, 2001.
[37] BROOKS S, GELMAN A, JONES G, et al. Handbook of Markov Chain Monte Carlo[M]. New York: CRC press, 2011.
[38] CHEN M H, SHAO Q M, IBRAHIM J G. Monte Carlo Methods in Bayesian Computation[M]. Springer Science & Business Media, 2012.
[39] GIUDICI P, GIVENS G H, MALLICK B K. Wiley Series in Computational Statistics[M]. Wiley Online Library, 2013.
[40] MARJORAM P, MOLITOR J, PLAGNOL V, et al. Markov chain Monte Carlo without likelihoods[J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(26): 15324-15328.
[41] SISSON S A, FAN Y, TANAKA M M. Sequential monte carlo without likelihoods[J]. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104(6): 1760-1765.
[42] FEARNHEAD P, PRANGLE D. Constructing summary statistics for approximate Bayesian computation: semi-automatic approximate Bayesian computation[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2012, 74(3): 419-474.
[43] DELMORAL P, DOUCET A, JASRA A. An adaptive sequential Monte Carlo method for approximate Bayesian computation[J]. Statistics and Computing, 2012, 22(5): 1009-1020.
[44] MENGERSEN K L, PUDLO P, ROBERT C P. Bayesian computation via empirical likelihood[J]. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(4): 1321-1326.
[45] SISSON S A, FAN Y, BEAUMONT M. Handbook of Approximate Bayesian Computation[M]. Chapman and Hall/CRC, 2018.
[46] FRAZIER D T, MARTIN G M, ROBERT C P. On consistency of approximate Bayesian computation[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1508.05178.pdf.
[47] HEIN J, SCHIERUP M, WIUF C. Gene Genealogies, Variation and Evolution: a Primer in Coalescent Theory[M]. Oxford: Oxford University Press, 2004.
[48] TANAKA M M, FRANCIS A R, LUCIANI F, et al. Using approximate Bayesian computation to estimate tuberculosis transmission parameters from genotype data[J]. Genetics, 2006, 173(3): 1511-1520.
[49] WOOD S N. Statistical inference for noisy nonlinear ecological dynamic systems[J]. Nature, 2010, 466(7310): 1102-1104.
[50] ZHU W C, FAN Y. A novel approach for Markov random field with intractable normalizing constant on large lattices[J]. Journal of Computational and Graphical Statistics, 2018, 27(1): 59-70.
[51] PRANGLE D. Summary Statistics[M]. Chapman and Hall/CRC, 2018.
[52] JOYCE P, MARJORAM P. Approximately sufficient statistics and Bayesian computation[J]. Statistical Applications in Genetics and Molecular Biology, 2008, 7(1). DOI: 10.2202/1544-6115.1389.
[53] HASTIE T, TIBSHIRANI R, FRIEDMAN J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction[M]. 2nd ed. New York: Springer, 2009.
[54] MARDIA K V, KENT J T, BIBBY J M. Multivariate analysis[M]//Probability and Mathematical Statistics. New York: Academic Press, 1979.
[55] JIANG B, WU T Y, ZHENG C, et al. Learning summary statistic for approximate Bayesian computation via deep neural network[J]. Statistica Sinica, 2017, 27(4): 1595-1618.
[56] CREEL M. Neural nets for indirect inference[J]. Econometrics and Statistics, 2017, 2: 36-49.
[57] RAYNAL L, MARIN J M, PUDLO P, et al. ABC random forests for Bayesian parameter inference[J]. Bioinformatics, 2018, 35(10): 1720-1728.
[58] BEAUMONT M A. Approximate Bayesian computation[J]. Annual Review of Statistics and Its Application, 2019, 6(1): 379-403.
[59] HARRISON J U, BAKER R E. An automatic adaptive method to combine summary statistics in approximate Bayesian computation[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1703.02341.pdf.
[60] BERNTON E, JACOB P E, GERBER M, et al. Approximate Bayesian computation with the wasserstein distance[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2019, 81(2): 235-269.
[61] PARK M, JITKRITTUM W, SEJDINOVIC D. K2-ABC: approximate Bayesian computation with kernel embeddings[C]//Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS). Cadiz, Spain, 2016.
[62] SISSON S A, FAN Y, TANAKA M M. Sequential monte carlo without likelihoods: errata[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(39): 1760-1765.
[63] BEAUMONT M A, CORNUET J M, MARIN J M, et al. Adaptive approximate Bayesian computation[J]. Biometrika, 2009, 96(4): 983-990.
[64] TONI T, WELCH D, STRELKOWA N, et al. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems[J]. Journal of the Royal Society Interface, 2009, 6(31): 187-202.
[65] DUANE S, KENNEDY A D, PENDLETON B J, et al. Hybrid Monte Carlo[J]. Physics letters B, 1987, 195(2): 216-222.
[66] MEEDS E, LEENDERS R, WELLING M. Hamiltonian ABC[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1503.01916.pdf.
[67] GIANNOPOULOS P, GODSILL S J. Estimation of car processes observed in noise using Bayesian inference[C]//2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Salt Lake City, UT, USA, 2001.
[68] JI C L, YANG L G, ZHU W C, et al. On Bayesian inference for continuous-time autoregressive models without likelihood[C]//2018 21st International Conference on Information Fusion (FUSION). 2018: 2137-2142.
[69] HARVEY A C. Forecasting, Structural Time Series Models and the Kalman Filter[M]. Cambridge: Cambridge University Press, 1991.
[70] JONES R H. Fitting a continuous time autoregression to discrete data[C]//Proceedings of the Second Applied Time Series Symposium Held. Tulsa, Oklahoma, 1980.
[71] SZÉKELY G J, RIZZO M L, BAKIROV N K. Measuring and testing dependence by correlation of distances[J]. The Annals of Statistics, 2007, 35(6): 2769-2794.
[72] LI C L, CHANG W C, CHENG Y, et al. MMD GAN: towards deeper understanding of moment matching network[C]//Advances in Neural Information Processing Systems 30 (NIPS 2017). 2017.
[73] HOFFMAN M D, BLEI D M, WANG C, et al. Stochastic variational inference[J]. Journal of Machine Learning Research, 2013, 14(1): 1303-1347.
[74] ZHAO S J, SONG J M, ERMON S. Infovae: information maximizing variational autoencoders[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1706.02262.pdf.
[75] MAKHZANI A, SHLENS J, JAITLY N, et al. Adversarial autoencoders[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1511.05644.pdf.
[76] MORENO A, ADEL T, MEEDS E, et al. Automatic variational ABC[R/OL]. [2019-08-26]. https://arxiv.org/pdf/1606.08549.pdf.
[77] 王小娥, 蔺小林, 李建全. 一类具有脉冲免疫治疗的HIV-1感染模型的动力学分析[J]. 应用数学和力学, 2019, 40(7): 728-740.(WANG Xiaoe, LIN Xiaolin, LI Jianquan. Dynamic analysis of a class of HIV-1 infection models with pulsed immunotherapy[J]. Applied Mathematics and Mechanics, 2019, 40(7): 728-740.(in Chinese))