引言
神经网络动力学模型的同步研究目前已成为现代应用数学研究领域的热点之一.它的动力学行为通常包括系统的渐近稳定性、鲁棒稳定性、局部或全局稳定性、同步稳定性、指数稳定性、周期解的存在性和多项式稳定性等[1-10].在神经网络动力学模型中的递归神经网络动力学模型作为一个成熟而广泛接受的网络动力学模型,目前越来越受到广大学者的重视.特别地, 递归神经网络动力学模型已成为图像处理分类、模式识别、信号处理、联想记忆、优化问题等理论和应用中最重要的课题之一[1-16].
然而, 在自然系统和人工系统中,时滞现象是普遍存在的.从文献[1-5]的结果可以看出,时滞对神经网络的实现有很大的不稳定影响.因此, 研究神经网络动力学模型时,应该把时滞引入到模型中, 这将与实际情况更加相似.例如,在文献[6-16]及其参考文献中,已经对时滞递归神经网络动力学模型做了一系列的研究.
众所周知,同步问题是神经网络动力学模型研究中最基本和最重要的问题之一.此外, 同步问题的研究在生物学、气候学、社会学、生态学等许多科学领域都发挥着极其重要的作用.目前,关于时滞神经网络动力学模型的同步研究,国内外有许多重要的工作.例如,文献[13-25]及其参考文献已经对时滞神经网络动力学模型同步研究方面做了深入的研究.
值得注意的是, 在研究混沌系统同步问题时, 同步收敛速度的估计是一个非常有趣和有用的方法.但是, 在某些情况下, 同步的收敛速度无法显示或很难估计.例如, 考虑下面的微分方程[22]:
虽然我们可以证明上述方程是渐近稳定的,但无法准确估计其解的收敛性.然而,最近在文献[22-25]中,通过引入新的同步概念,即一般衰减同步(GDS),研究了一类具有连续激活的混沌神经网络的同步问题.这使得需要考虑一种新的收敛速度,即一般衰减同步.另一方面,对于具有分布时滞的递归神经网络的一般衰减同步的研究目前还相当少,因此,基于以上分析和原因,本文将研究以下具有分布时滞的递归神经网络动力学模型:
(1)
其中i∈I {1,2,…,n}, n≥2是神经网络单位的数目; xi(t)为第i个神经元的状态变量;ci>0为正的常数;aij, bij和dij分别是在第个i神经元和第j个神经元之间的连接权重;fi(·),gi(·)和hi(·)是非线性激活函数, Ii是外部输出常数;τj(t)和σj(t)是传输时滞且满足0≤τi(t)≤τi,0≤σi(t)≤σi.本文的主要目的是通过应用文献[23-25]的方法和构造适当的Lyapunov-Krasovskii函数,研究得到模型(1)的一般衰减同步的充分条件.本文通过设计一种新的控制函数,构造多个Lyapunov-Krasovskii函数以及采用有效的分析方法,实现了具有分布时滞的递归神经网络动力学模型的一般衰减同步,并改进和推广了目前已有的工作.
{1,2,…,n}, n≥2是神经网络单位的数目; xi(t)为第i个神经元的状态变量;ci>0为正的常数;aij, bij和dij分别是在第个i神经元和第j个神经元之间的连接权重;fi(·),gi(·)和hi(·)是非线性激活函数, Ii是外部输出常数;τj(t)和σj(t)是传输时滞且满足0≤τi(t)≤τi,0≤σi(t)≤σi.本文的主要目的是通过应用文献[23-25]的方法和构造适当的Lyapunov-Krasovskii函数,研究得到模型(1)的一般衰减同步的充分条件.本文通过设计一种新的控制函数,构造多个Lyapunov-Krasovskii函数以及采用有效的分析方法,实现了具有分布时滞的递归神经网络动力学模型的一般衰减同步,并改进和推广了目前已有的工作.
1 预 备 知 识
本文总是使用I {1,2,…,n}.假设系统(1)只满足下面的初始条件:
{1,2,…,n}.假设系统(1)只满足下面的初始条件:
xi(s)=φi(s), s∈[-τ,0], i=1,2,…,n,
其中τ=maxj∈I{τj,σj},φ(s)=(φ1(s), φ2(s), …, φn(s))∈C([-τ,0],R),表示在区间[-τ,0]映射到R的所有连续函数的Banach空间,其中范数定义为
令Rn是n维向量空间.对于任意向量v=(v1,v1,…, vn)T∈ Rn的二范数定义为
本文引入了以下假设.
(H1) 对于每个j∈![]() ,激活函数fj(u),gj(u), hj(u)是连续的且存在常数Lj, Hj,Kj,Nj,Mj,Oj>0,使得
,激活函数fj(u),gj(u), hj(u)是连续的且存在常数Lj, Hj,Kj,Nj,Mj,Oj>0,使得
|fj(v1)-fj(v2)|≤Lj|v1-v2|+Nj, |gj(v1)-gj(v2)|≤Hj|v1-v2|+Mj,
|hj(v1)-hj(v2)|≤Kj|v1-v2|+Oj, v1,v2∈R.
(H2) 时滞τj(t)和σj(t)是可微的,且存在常数0≤ξj≤1/2,0≤γj≤1/2使得
本文中,考虑系统(1)为驱动系统, 则有以下的响应系统:
(2)
其中ui(t)是将要构造的控制函数.
令ei(t)=yi(t)-xi(t),那么联合系统(1)和(2),得到以下的误差系统:
(3)
其中![]() 现在将给出ψ-类型函数和一般衰减同步的定义.
现在将给出ψ-类型函数和一般衰减同步的定义.
定义1[23-24] 称函数ψ:R+→[1,+∞)是ψ-类型函数, 如果它满足以下条件:
1) ψ是可微的且非递减函数;
2) ψ(0)=1且ψ(+∞)=+∞;
![]() 是非递减函数且
是非递减函数且![]() 其中
其中![]() 是ψ(t)对时间t的导数;
是ψ(t)对时间t的导数;
4) 对任意t,s≥0, ψ(t+s)≤ψ(t)ψ(s).
显然,函数ψ(t)=eαt与ψ(t)=(1+t)α对任意α> 0满足以上4个条件,因此函数ψ(t)=eαt与ψ(t)=(1+t)α是ψ-类型函数.
定义2[23-24] 称驱动系统(1)和响应系统(2)是实现一般衰减同步,如果存在一个常数ε>0和ψ-类型函数ψ使得对系统(1)和(2)任意的解x(t)=(x1(t),x2(t),…,xn(t))与y(t)=(y1(t),y2(t),…,yn(t)),可以得到
其中ε是误差函数的收敛值趋于0的速度.
(H3) 对于在定义1中给出定义的函数![]() 存在一个函数
存在一个函数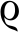 (t)∈C(R,R+)和常数δ使得对任意t≥0有
(t)∈C(R,R+)和常数δ使得对任意t≥0有
![]()
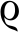 (s)ds<+∞.
(s)ds<+∞.
(4)
下面介绍一个重要的引理, 在第2节将应用这个引理得到本文的主要结果.
引理1[23-24] 在假设(H3)成立的条件下,设系统(1)和系统(2)的误差函数e(t)=y(t)-x(t) 满足微分方程![]() 其中et=e(t+s), s∈[-τ,0], 并且g(t,et)是局部有界的.如果存在可微函数V(t,et): R+×C→R+,和正常数λ1, λ2使得对任意(t,et)∈R+×C得到
其中et=e(t+s), s∈[-τ,0], 并且g(t,et)是局部有界的.如果存在可微函数V(t,et): R+×C→R+,和正常数λ1, λ2使得对任意(t,et)∈R+×C得到
![]()
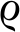 (t),
(t),
(5)
其中x(t)和y(t)分别是系统(1)和(2)的解,并且δ>0和 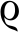 (t)是在假设(H3)中给定的.那么,驱动系统(1)和响应系统(2)在定义2的意义下实现一般衰减同步,其收敛速度为δ/2.
(t)是在假设(H3)中给定的.那么,驱动系统(1)和响应系统(2)在定义2的意义下实现一般衰减同步,其收敛速度为δ/2.
2 主 要 结 果
本节将研究得到驱动系统(1)和响应系统(2)实现一般衰减同步的充分条件.首先构造一个非线性控制函数:
(6)
其中i, j∈I且βi满足
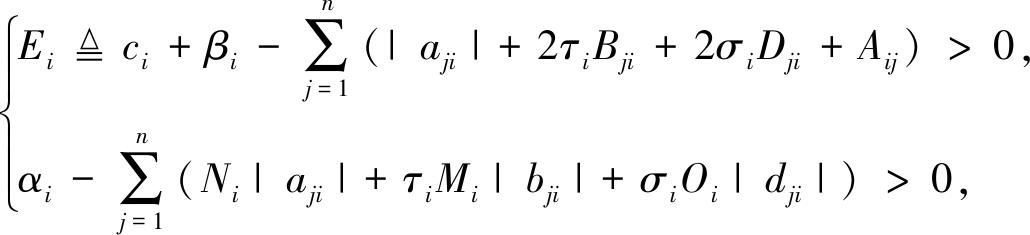
(7)
其中Cij>0和Dij>0是常数,Bij=|bij|Hj,Dij=|dij|Kj, Aij=(Cijτij+Dijσij)/2.
下面基于非线性控制器(6),得到以下主要结论.
定理1 设假设(H1)~(H3)成立,并且基于控制函数ui(t)满足式(7),则驱动系统(1)和响应系统(2)可实现一般衰减同步.
证明 首先,构造Lyapunov-Krasovskii函数:
(8)
沿着系统(3)计算V1(t)的导数得到
(9)
由假设(H1),可以得到
(10)
类似地,可以得到
(11)
(12)
由假设(H2)和式(7)、(9)~(12),可以得到
(13)
其次,构造以下的Lyapunov-Krasovskii函数:
![]() (
( )|d
)|d dθds+
dθds+
![]() (
( )|d
)|d dθds.
dθds.
计算V2(t)的导数,得到
(14)
其中
最后,构造如下的Lyapunov-Krasovskii函数:
V(t)=V1(t)+V2(t),
则存在常数χ> 1,使得
(15)
其中 E=mini∈I{Ei} .
计算V(t)的导数并由式(13)、(14)得到
令β=maxi∈I{βi}>0,并利用不等式0≤ab/(a + b) ≤a,对任意a>0,b>0,得到
![]()
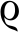 (t) -A.
(t) -A.
(16)
下一步, 取一个充分小的一个常数δ使得δχ<E,则由不等式(15)和(16)可以得到
![]()
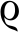
![]()
![]()
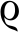 (t)≤β
(t)≤β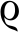 (t).
(t).
进一步得到
![]()
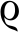 (t).
(t).
(17)
因此,由引理1可以得到驱动系统(1)和响应系统(2)可实现一般衰减同步.其中误差函数(3)的收敛值趋于0的速度为δ/2.下面将讨论一些特殊情况.
如果在假设(H1)中假设激活函数fj(u),gj(u),hj(u)满足全局Lipschitz条件,即假设(H1)中的常数Nj=Mj=Oj=0,则假设(H1)变成以下的新假设.
(H1)′ 激活函数fj(u),gj(u),hj(u)满足全局Lipschitz条件,即存在常数Lj,Hj,Kj>0,使得
|fj(v1)-fj(v2)|≤Lj|v1-v2|, |gj(v1)-gj(v2)|≤Hj|v1-v2|,
|hj(v1)-hj(v2)|≤Kj|v1-v2|,
其中 v1,v2∈R.
此外,控制函数(6)和不等式(7)变成式(18)、(19):
(18)
(19)
由定理1的结论,可得到下面的推论.
推论1 设假设(H1)′、(H2)、(H3)成立并且基于控制函数(18)满足式(19),则驱动系统(1)和响应系统(2)可实现一般衰减同步.
注1 函数ψ用作衰减函数, 所以ψ-类型稳定性也被称为具有一般衰减率的稳定性.当ψ(t)=eαt , ψ(t)=(1 + t)α和ψ(t)=1+αln(1+t)对于任何α> 0时, ψ-类型稳定性可化为指数同步、多项式同步和对数同步.
注2 在文献[23-24]中构造了如下的控制函数:
并实现了所研究系统的一般衰减同步,其中G1=diag(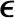 1,
1,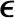 2,…,
2,…,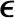 n),G2=diag(ε1,ε2,…,εn).然而,本文构造了更简单、更有效的控制函数(6)和(18).因此,本文的结果可以看作是对文献[23-24]所得结果的改进和推广.
n),G2=diag(ε1,ε2,…,εn).然而,本文构造了更简单、更有效的控制函数(6)和(18).因此,本文的结果可以看作是对文献[23-24]所得结果的改进和推广.
3 数 值 示 例
例 考虑下面的含分布时滞的递归神经网络系统:
(20)
对应的响应系统为
(21)
其中i=1,2, f1(u)=f2(u)=th(u), g1(u)=g2(u)=th(u)-sh(u), h1(u)=h2(u)=th(u)-ch(u), c1=c2=1, a11=1.25, a12=-0.11, a21=-2.5, a22=3.2, b11=-1.6, b12=-0.1, b21=0.18, b22=-2, d11=0.2, d12=0, d21=-0.2, d22=0.15, τj(t)=et/(1+et), σj(t)=et/(5+et), Ii=0.
以下是非线性控制函数ui(t):
(22)
其中ei(t)=yi(t)-xi(t)且i=1,2.如果取Lj=Hj=Kj=1, Nj=0.05,Mj=0.03,Oj=0.032且τj=σj=1,那么计算得到假设(H1)和(H2)成立.进一步地,令 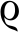 (t)=e-0.1t, ψ(t)=et且α1=0.5, α2=0.55, β1=7, β2=6.则假设(H3)和不等式(7)成立,从而定理1的全部条件成立.因此,根据定理1,可以基于控制函数(22)、驱动系统(20)和响应系统(21)实现一般衰减同步.系统(20)和(21)之间同步误差曲线和同步轨迹曲线的数值模拟图如图1~4所示.
(t)=e-0.1t, ψ(t)=et且α1=0.5, α2=0.55, β1=7, β2=6.则假设(H3)和不等式(7)成立,从而定理1的全部条件成立.因此,根据定理1,可以基于控制函数(22)、驱动系统(20)和响应系统(21)实现一般衰减同步.系统(20)和(21)之间同步误差曲线和同步轨迹曲线的数值模拟图如图1~4所示.
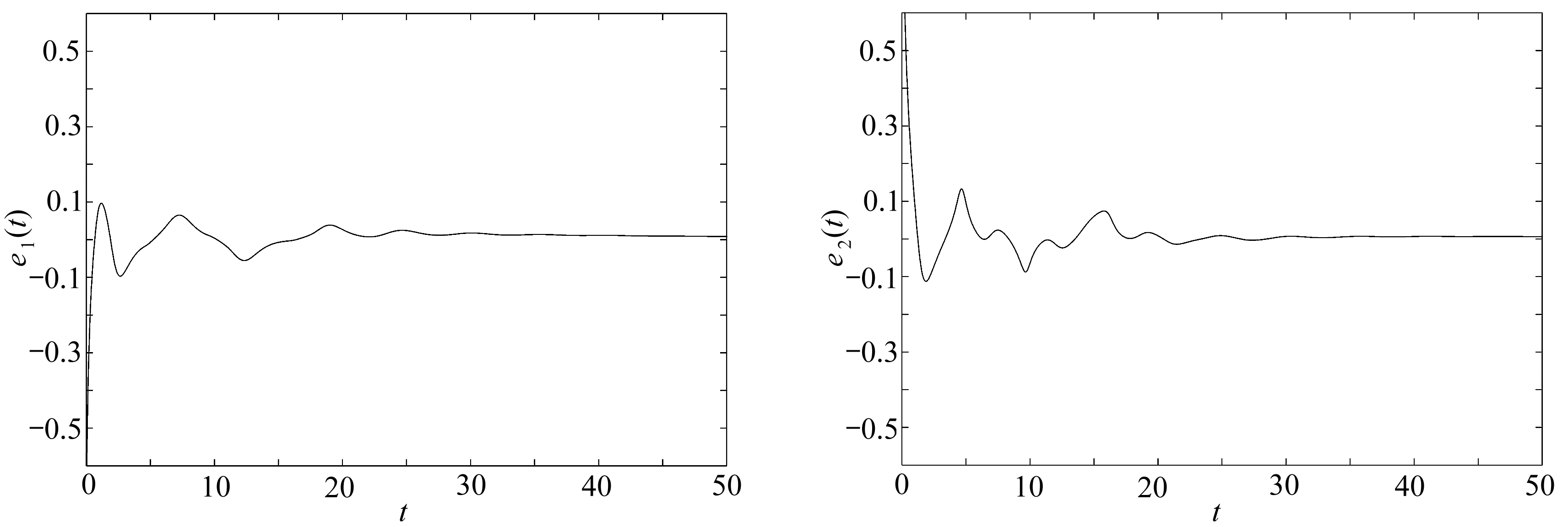
图1 同步误差e1(t) 图2 同步误差e2(t)
Fig. 1 Synchronization error e1(t) Fig. 2 Synchronization error e2(t)
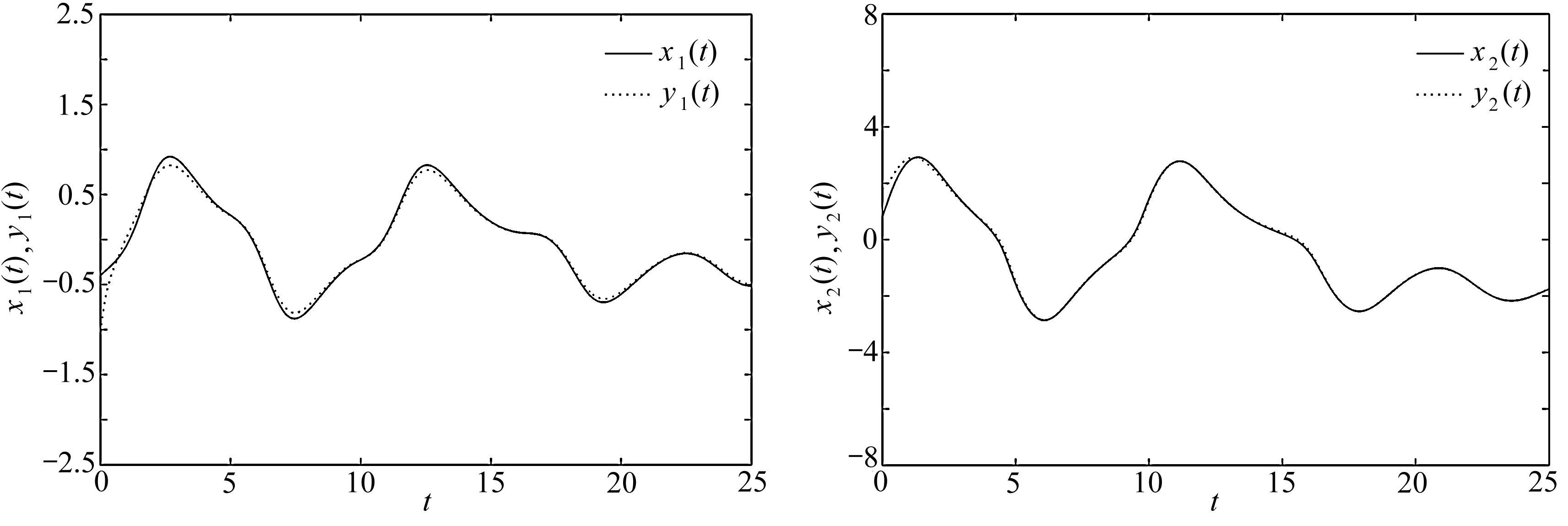
图3 状态变量x1(t), y1(t)的同步轨迹 图4 状态变量x2(t), y2(t)的同步轨迹
Fig. 3 Synchronization curves of x1(t), y1(t) Fig. 4 Synchronization curves of x2(t), y2(t)
4 总 结
本文基于文献[23-25]的方法,构造了适当的Lyapunov-Krasovskii函数,研究得到了驱动系统(1)和响应系统(2)达到一般衰减同步的充分条件.然后针对本文得到的理论结果给出了例子和数值模拟.因为在本文注1中提到的ψ-类型稳定性也被称为具有一般衰减率的稳定性,并且ψ-类型稳定性可化为指数同步、多项式同步和对数同步,因此,本文研究得到的结论改进和推广了目前已有神经网络同步研究方面的工作.
[1] ZENG Z G, WANG J, LIAO X X. Global exponential stability of a general class of recurrent neural networks with time-varying delays[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2003, 50(10): 1353-1358.
[2] CAO J D, WANG J. Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays[J]. Neural Networks, 2004, 17(3): 379-390.
[3] CHEN B S, WANG J. Global exponential periodicity of a class of recurrent neural networks with oscillating parameters and time-varying delays[J]. IEEE Transactions on Neural Networks, 2005, 16(6): 1440-1448.
[4] CAO J D, WANG J. Global asymptotic and robust stability of recurrent neural networks with time delays[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2005, 52(2): 417-426.
[5] LI C G, LIAO X F. Robust stability and robust periodicity of delayed recurrent neural networks with noise disturbance[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2006, 53(10): 2265-2273.
[6] HUANG X, CAO J D, DANIEL W C H. Existence and attractivity of almost periodic solution for recurrent neural networks with unbounded delays and variable coefficients[J]. Nonlinear Dynamics, 2006, 45(3/4): 337-351.
[7] ZHANG H G, WANG Z S, LIU D R. Global asymptotic stability of recurrent neural networks with multiple time-varying delays[J]. IEEE Transactions on Neural Networks, 2008, 19(5): 855-873.
[8] LOU X Y, CUI B T. Delay-dependent criteria for global robust periodicity of uncertain switched recurrent neural networks with time-varying delay[J]. IEEE Transactions on Neural Networks, 2008, 19(4): 549-557.
[9] HU J, WANG J. Global stability of complex-valued recurrent neural networks with time-delays[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(6): 853-865.
[10] SUN J, CHEN J. Stability analysis of static recurrent neural networks with interval time-varying delay[J]. Applied Mathematics and Computation, 2013, 221: 111-120.
[11] WEN S P, ZENG Z G, HUANG T W, et al. Passivity analysis of memristor-based recurrent neural networks with time-varying delays[J]. Journal of the Franklin Institute, 2013, 350(8): 2354-2370.
[12] ZHOU L Q, ZHANG Y Y. Global exponential periodicity and stability of recurrent neural networks with multi-proportional delays[J]. ISA Transactions, 2016, 60: 89-95.
[13] WU A L, WEN S P, ZENG Z G. Synchronization control of a class of memristor-based recurrent neural networks[J]. Information Sciences, 2012, 183: 106-116.
[14] JIANG M H, WANG S T, MEI J, et al. Finite-time synchronization control of a class of memristor-based recurrent neural networks[J]. Neural Networks, 2015, 63: 133-140.
[15] WU A L, ZENG Z G, ZHU X S, et al. Exponential synchronization of memristor-based recurrent neural networks with time delays[J]. Neurocomputing, 2011, 74: 3043-3050.
[16] LI T, FEI S M, ZHANG K J. Synchronization control of recurrent neural networks with distributed delays[J]. Physica A: Statistical Mechanics and Its Applications, 2008, 387: 982-996.
[17] ABDURAHMAN A, JIANG H J, TENG Z D. Lag synchronization for Cohen-Grossberg neural networks with mixed time-delays via periodically intermittent control[J]. International Journal of Computer Mathematics, 2017, 94: 275-295.
[18] MUHAMMADHAJI A, ABDURAHMAN A, JIANG H J. Finite-time synchronization of complex dynamical networks with time-varying delays and nonidentical nodes[J]. Journal of Control Science and Engineering, 2017, 2017: 1-13. DOI: 10.1155/2017/5072308.
[19] HU C, JIANG H J, TENG Z D. Fuzzy impulsive control and synchronization of general chaotic system[J]. Acta Applicandae Mathematicae, 2010, 109(2): 463-485.
[20] HU M F, XU Z Y. Adaptive feedback controller for projective synchronization[J]. Nonlinear Analysis: Real World Applications, 2008, 9(3): 1253-1260.
[21] 张玮玮, 陈定元, 吴然超, 等. 一类基于忆阻器分数阶时滞神经网络的修正投影同步[J]. 应用数学和力学, 2018, 39(2): 239-248. (ZHANG Weiwei, CHEN Dingyuan, WU Ranchao, et al. Modified-projective-synchronization of memristor-based fractional-order delayed neural networks[J]. Applied Mathematics and Mechanics, 2018, 39(2): 239-248. (in Chinese))
[22] SADER M, ABDURAHMAN A, JIANG H J. General decay lag synchronization for competitive neural networks with constant delays[J]. Neural Process Letters, 2019, 50(1): 445-457.
[23] WANG L M, SHEN Y, ZHANG G D. Synchronization of a class of switched neural networks with time-varying delays via nonlinear feedback control[J]. IEEE Trans Cyber, 2016, 46(10): 2300-2310.
[24] WANG L M, SHEN Y, ZHANG G D. General decay synchronization stability for a class of delayed chaotic neural networks with discontinuous activations[J]. Neurocomputing, 2016, 179: 169-175.
[25] ABDURAHMAN A, JIANG H J, HU C. General decay synchronization of memristor-based Cohen-Grossberg neural networks with mixed time-delays and discontinuous activations[J]. Journal of the Franklin Institute, 2017, 354(15): 7028-7052.