引言
神经网络技术是20世纪末迅速发展起来的一门高新技术.由于神经网络具有良好的非线性映射能力、自学习适应能力, 为解决不确定非线性系统的建模和控制问题提供了一条新的思路, 吸引了国内外的众多学者和工程技术人员从事神经网络控制的研究.因此, 神经网络控制逐步发展成为智能控制的一个重要分支.
根据神经网络处理数据的类型, 可将其分为实数神经网络(RVNNs)和复数神经网络(CVNNs).虽然RVNNs 已在诸多领域得到了应用, 但其在实现几何变换(例如二维(2D)仿射变换)和对称问题的检测和排除OR(XOR)方面表现较差[1-3].学者们发现在这些实际应用中需要处理更高维度的数据.作为RVNNs的通用扩展, CVNNs具有更复杂的特性, 因此CVNNs被提出[4].目前, CVNNs因其在计算机视觉与遥感、量子装置、生理神经装置和系统的时空分析中的综合应用而受到广泛关注[5-7].同时, 当神经网络被用于系统硬件实现时, 由于放大器转换速度的限制, 神经网络中其当前状态不可避免地受到过去状态的影响.即当前状态的变化率不仅与当前时刻的状态有关, 而且也依赖于过去某时刻或某段时间的状态.这种时间延迟经常是导致模型不稳定性、振荡或其他不良性能的主要来源之一[8-10].因此, 具有时间延迟的神经网络的动力学行为引起了许多学者的关注, 并且已经得到了许多有意义的成果[11-13].然而,这些文献大多数研究的是具有单个延迟的模型.通常, 在实际情况中, 从一个点传输到另一个点的信号可能会经历一些网络段, 由于可变的网络传输条件, 可能会导致不同属性的时间延迟.例如,在状态反馈网络控制中, 物理设备、控制器、传感器和执行器位于不同的位置, 信号从一个设备传输到另一个设备时, 将发生两个附加的时变延迟:一个是从传感器到控制器、另一个是从控制器到执行器[14].因此,研究具有加性时变时滞的CVNNs动力学行为具有重要意义.
一般而言, 由于神经网络的复杂性和技术限制, 完全获得有关网络输出中神经元状态的信息是不可行的[15].特别是在规模较大的神经网络中, 通常获得的只是神经元状态的部分信息.为了充分利用神经元的状态以实现一些重要的性能, 有必要通过可用的输出测量来估计神经元状态.目前, 对于神经网络的状态估计问题, 已经报道了大量结果[15-21].文献[17]假定不确定性参数是范数有界的, 基于一种新的边界技术, 研究了一类具有时变时滞的不确定神经网络的鲁棒状态估计问题.文献[18-19]通过构造合适的Lyapunov-Krasovskii泛函, 利用Newton-Leibniz公式和线性矩阵不等式(LMI)技术, 讨论了具有离散区间时变时滞和分布时变时滞的神经网络的状态估计问题.文献[20]研究了具有多次衰落测量的离散时间忆阻神经网络的H∞状态估计器的设计问题.文献[21]通过选择适当的Lyapunov-Krasovskii泛函并利用倒数凸组合法和矩阵不等式技术, 研究了具有两个加性离散时变时滞的复数神经网络的状态估计问题.鉴于此, 本文拟将研究具有泄漏时滞、加性离散时变时滞、加性分布时变时滞的复数神经网络的状态估计问题, 并给出网络状态估计的不等式判据.相比已有文献, 本文的贡献主要体现在3个方面:
1) 本文推广了文献[21]的结果,当本文的泄漏时滞为0, 并且不考虑加性分布时变时滞时,就可以得到文献[21]中的结果;
2) 文中考虑的模型是在不要求CVNNs的激活函数分解为实部与虚部的条件下研究的, 其得到的结果以复数线性矩阵不等式(CVLMI)的形式给出;
3) 利用泄漏时滞、加性离散时变时滞、加性分布时变时滞的全部信息构造适当的Lyapunov-Krasovskii泛函.
本文的结构如下: 第1节介绍了相关的预备知识, 包括神经网络模型、相关的假设及引理; 第2节给出了具有泄漏时滞、混合加性时变时滞复数神经网络全局渐近稳定的充分性判据; 第3节通过一个数值仿真实例验证了提出理论的有效性; 最后总结了全文所做的工作.
1 预 备 知 识
本文中做如下符号说明:![]() 表示相应维度的单位矩阵;R, C分别表示实数域、复数域;Rn, Cn分别表示由n维实数、复数向量构成的空间;Rn×m, Cn×m分别表示由n×m维实数、复数矩阵构成的集合.X≥Y(X>Y)表示X-Y是半正定的(正定的);“T”“*” 分别表示矩阵的转置、矩阵的共轭转置.
表示相应维度的单位矩阵;R, C分别表示实数域、复数域;Rn, Cn分别表示由n维实数、复数向量构成的空间;Rn×m, Cn×m分别表示由n×m维实数、复数矩阵构成的集合.X≥Y(X>Y)表示X-Y是半正定的(正定的);“T”“*” 分别表示矩阵的转置、矩阵的共轭转置.
1.1 模型及基本引理介绍
考虑如下具有泄漏时滞和混合加性时变时滞的CVNNs:
C![]() f(w(s))ds+J(t),
f(w(s))ds+J(t),
(1)
式中t≥0, w(t)=(w1(t),w2(t),…,wn(t))T∈Cn表示在t时刻的n个神经元状态向量;自反馈连接权矩阵D=diag(d1,d2,…,dn)∈Rn×n且di>0 (i=1,2,…,n);A=(aij)n×n∈Cn×n ,B=(bij)n×n∈Cn×n,C=(cij)n×n∈Cn×n(i, j=1,2,…,n)分别为连接权矩阵、离散时变时滞连接权矩阵和分布时变时滞连接权矩阵;外部输入J=(J1,J2,…,Jn)T∈Cn; f(w(t))=(f1(w1(t)), f2(w2(t)), …, fn(wn(t)))T∈Cn表示神经元激活函数;泄漏时滞δ>0, 加性离散时变时滞、分布时变时滞分别为di(t), βi(t)(i=1,2), 满足0≤di(t)≤di,0≤βi(t)≤βi(i=1,2), 其中di, βi 是连续的实数,并且d(t)=d1(t)+d2(t), d=d1+d2,β(t)=β1(t)+β2(t), β=β1+β2.CVNNs(1)的初值条件为
w(s)=φ(s), s∈[-h,0],
其中φ∈Cn在[-h,0]上是连续的, 并且h=max{d, β, δ}.
众所周知, 神经元状态的信息通常不完全来自应用中的网络测量(输出), 并且网络测量受到非线性干扰.因此假设网络测量满足
m(t)=Ew(t)+Fz(t, w(t)),
(2)
其中m(t)∈Cm表示测量输出,E∈Cm×n, F∈Cm×m是已知的连接权矩阵, z=(z1, z2, …, zm)T: R×Cn→Cm表示网络输出上的神经元非线性干扰.
建立CVNNs(1)相应的状态估计模型如下:
C![]() f(v(s))ds+J(t)+K(m(t)-n(t)),
f(v(s))ds+J(t)+K(m(t)-n(t)),
(3)
n(t)=Ev(t)+Fz(t,v(t)),
(4)
其中v(t)是模型(1)的状态估计量, 并且K∈Cn×m表示估计量的增益矩阵.
令h(t)=w(t)-v(t),则误差状态模型为
(5)
其中![]()
下文将讨论增益矩阵K的存在问题, 使得误差状态模型(5)全局渐近稳定.
为了获得主要结果, 本文需要如下假设.
假设1 激活函数fi(·)是连续的,并且对任意α1,α2∈C,存在γi∈R,i=1,2,…,n,有
|fi(α1)-fi(α2)|≤γi |α1-α2|,
令Γ=diag(γ1, γ2, …, γn).
假设2 对任意的μ1,μ2∈Cn, 存在一个常数矩阵L=(L1, L2,…, Lm)∈Rn×m, i=1,2,…,m,满足
引理1[21] X∈Cn×m是一个正定的Hermite矩阵,常数函数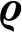 :[a,b]→Cn,并且a≤b,则有
:[a,b]→Cn,并且a≤b,则有
![]()
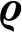
![]()
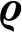
![]()
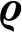 *(s)X
*(s)X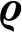 (s)ds.
(s)ds.
引理2[21] 对任意的向量ζ∈Cm, α∈(0,1), 正定矩阵Q∈Cn×n, 矩阵W1, W2∈Cn×m, Y∈Cn×n, 如果Y满足条件
则下列不等式成立:
2 主 要 结 果
定理1 在假设1和假设2成立的条件下, 如果存在正定的对角矩阵Mi(i=1,2,3,4), G∈Rn×n,正定的Hermite矩阵Pi∈Cn×n(i=1,2,…,10)以及复数矩阵R11, R12, R13, R22,R23,R33, S11, S12, S22, T11, T12,T22, W1, W2,W3, W4, Q,使得以下LMIs满足
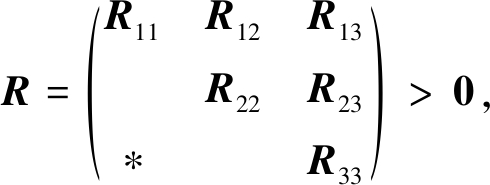
(6)
(7)
(8)
(9)
(10)
(11)
(12)
Ω=(Ωij)20×20<0,
(13)
其中
Ω12=R11-Q*-UE+P1, Ω13=-QD, Ω1,12=QA, Ω1,15=QB, Ω1,16=R12,
Ω1,17=R13, Ω1,18=QC, Ω1,19=-P1D, Ω1,20=-UF,
Ω2,19=D*P1D, Ω2,20=-UF, Ω33=-P2, Ω3,19=-D*P1D,
Ω44=T11-S11-P6+Γ*M2Γ, Ω46=P6-W1, Ω4,13=T12-S12,
Ω4,16=-R22, Ω4,17=-R23, Ω55=-T11-P7+Γ*M3Γ, Ω57=P7-W2,
Ω12,12=S22+β2P8-M1, Ω13,13=T22-S22-M2, Ω14,14=-T22-M3,
Ω15,15=-M4, Ω16,16=-P4, Ω17,17=-P5, Ω18,18=-P8,
Ω19,19=-P3, Ω20,20=-G,
其他的Ωij=0,那么就说CVNNs(1)的误差状态模型(5)是全局渐近稳定的.并且估计量的增益矩阵K定义为K=Q-1U.
证明 令![]() 构造如下的Lyapunov-Krasovskii函数:
构造如下的Lyapunov-Krasovskii函数:
V(t)=V1(t)+V2(t)+V3(t)+V4(t)+V5(t)+V6(t)+V7(t)+V8(t),
(14)
其中
V3(t)=ξ*(t)Rξ(t),
V4(t)=![]() η*(s)Sη(s)ds+
η*(s)Sη(s)ds+![]() η*(s)Tη(s)ds,
η*(s)Tη(s)ds,
![]()
 ,
,
沿着模型(5)求V(t)的导数, 根据引理1,有
h*(t-δ)D*P1h(t)+h*(t)P1Dh(t-δ)+
(15)
δ![]() [h*(t)P3h(t)-h*(t-u)P3h(t-u)]du≤
[h*(t)P3h(t)-h*(t-u)P3h(t-u)]du≤
h*(t)(P2+δ2P3)h(t)+h*(t-δ)(-P2)h(t-δ)+
(16)
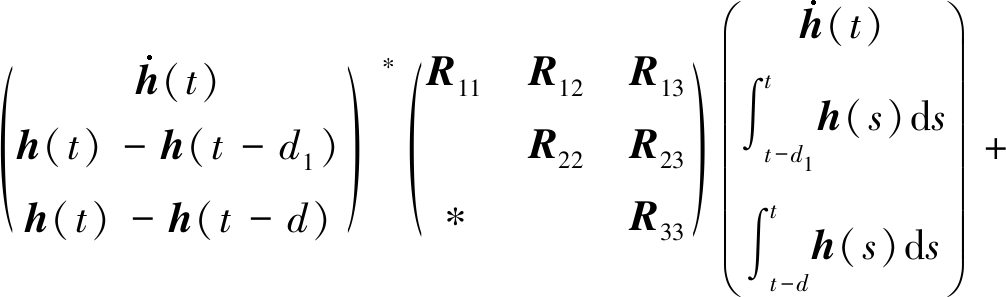
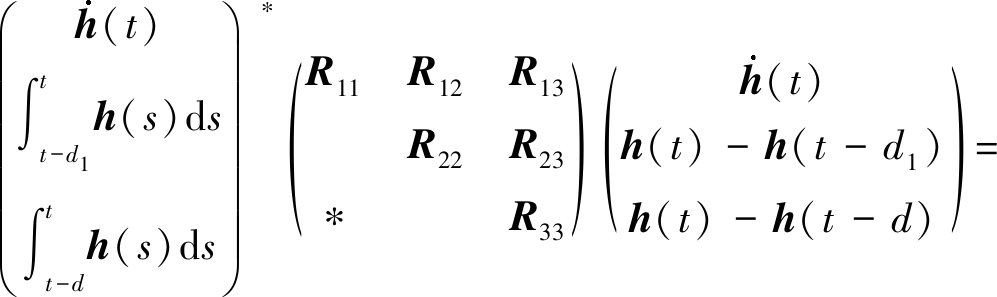
(17)
g*(h(t))S22g(h(t))+h*(t-d1)(T11-S11)h(t-d1)+
g*(h(t-d1))(T22-S22)g(h(t-d1))-h*(t-d)T11h(t-d)-
g*(h(t-d))T22g(h(t-d)),
(18)
d1![]() h*(s)P4h(s)ds-d
h*(s)P4h(s)ds-d![]() h* (s)P5h(s)ds≤
h* (s)P5h(s)ds≤
(19)
(20)
β2g*(h(t))P8g(h(t))-β(t)![]() g*(h(s))P8g(h(s))ds≤
g*(h(s))P8g(h(s))ds≤
(21)
(22)
基于引理1和引理2, 有
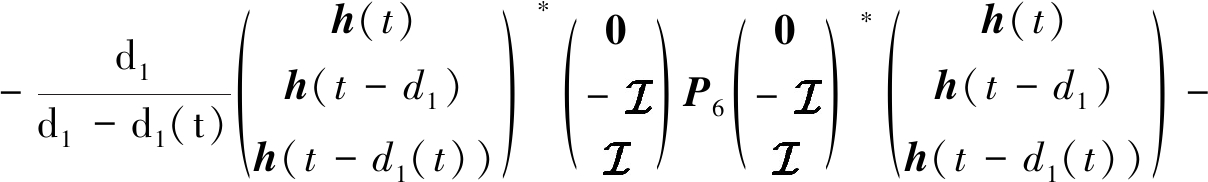
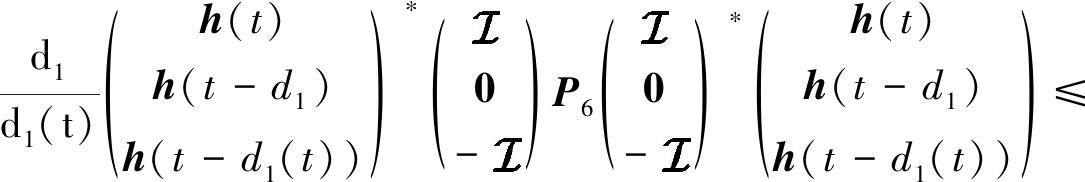


(23)
同理可得
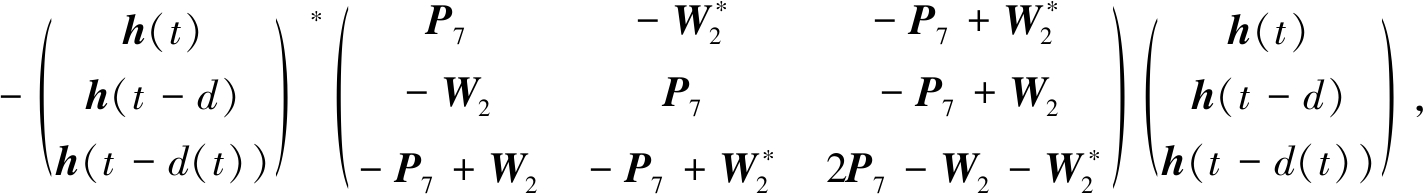
(24)
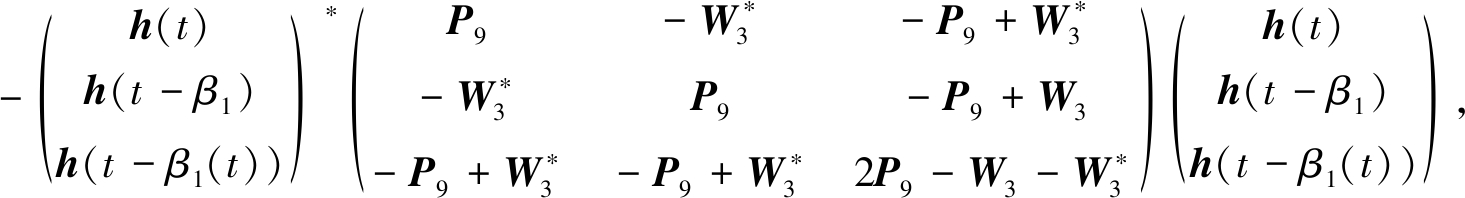
(25)

(26)
另外, 由假设1和假设2可得
0≤h*(t)Γ*M1Γh(t)-g*(h(t))M1g(h(t)),
(27)
0≤h*(t-d1)Γ*M2Γh(t-d1)-g*(h(t-d1))M2g(h(t-d1)),
(28)
0≤h*(t-d)Γ*M3Γh(t-d)-g*(h(t-d))M3g(h(t-d)),
(29)
0≤h*(t-d(t))Γ*M4Γh(t-d(t))-
g*(h(t-d(t)))M4g(h(t-d(t))),
(30)
(31)
采用自由权矩阵得到
(32)
由式(15)~(32)相加可得
(33)
其中
![]()
h(t-d(t)), h(t-β1), h(t-β), h(t-β1(t)),
h(t-β(t)), g(h(t)), g(h(t-d1)), g(h(t-d)),
g(h(t-d(t))), ![]() h(s)ds,
h(s)ds, ![]() h(s)ds,
h(s)ds, ![]() g(h(s))ds,
g(h(s))ds,
因此, 由式(13)和(33)可得
(34)
所以, 误差状态模型(5)是全局渐近稳定的, 证毕.
□
3 数 值 仿 真
考虑以下具有二维神经元的CVNNs(1)模型:
δ=0.3, D=diag(0.1, 0.2), f1(w)=f2(w)=0.3tanh(w),
d1(t)=0.2|sin(2t)|, d2(t)=0.2|cos(4t)|,
β1(t)=0.1|sin(3t)|, β2(t)=0.2|cos(2t)|.
因此, 当Γ=diag(0.3,0.3), d1=0.2,d=0.4,β1=0.1,β=0.3时, 满足假设1中的条件.
网络输出测量(2)考虑如下:
z1(t,w(t))=t+0.1w1(t)+0.2w2(t), z2(t,w(t))=t-0.1w1(t)+0.3w2(t),
当![]() 时, 容易验证假设2 满足.运用MATLAB 工具箱YALMIP, 可求解LMI(13), 得
时, 容易验证假设2 满足.运用MATLAB 工具箱YALMIP, 可求解LMI(13), 得
P1=![]()
P3=![]()
![]()
![]()
M1=diag(166.37, 125.08), M2=diag(30.90, 29.11), M3=diag(16.05, 15.41),
M4=diag(91.42, 79.38), G=diag(30.78, 34.29).
根据K=Q-1U,得
根据定理1, CVNNs(1)的误差状态模型(5)是全局渐近稳定的.CVNNs(1)的初值为w(t)=[2.4-3i 4-2i]T,CVNNs(3)的初值为v(t)=[0.5-4i 1.3-3i]T.仿真结果图1、2验证了用于设计延迟CVNNs状态估计器的方法的有效性.
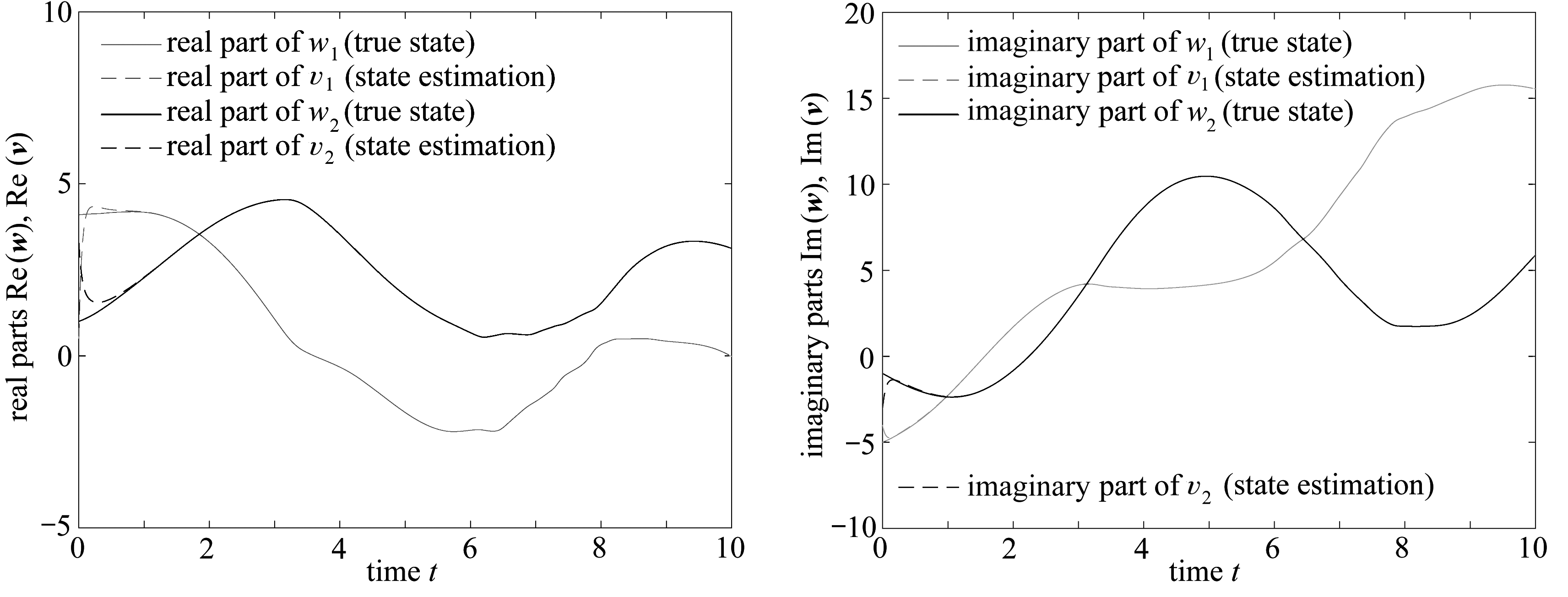
图1 神经元状态w(t)和估计状态v(t)的实部、虚部状态轨迹
Fig. 1 State trajectories of real and imaginary parts for neuronal state w(t) and estimation state v(t)
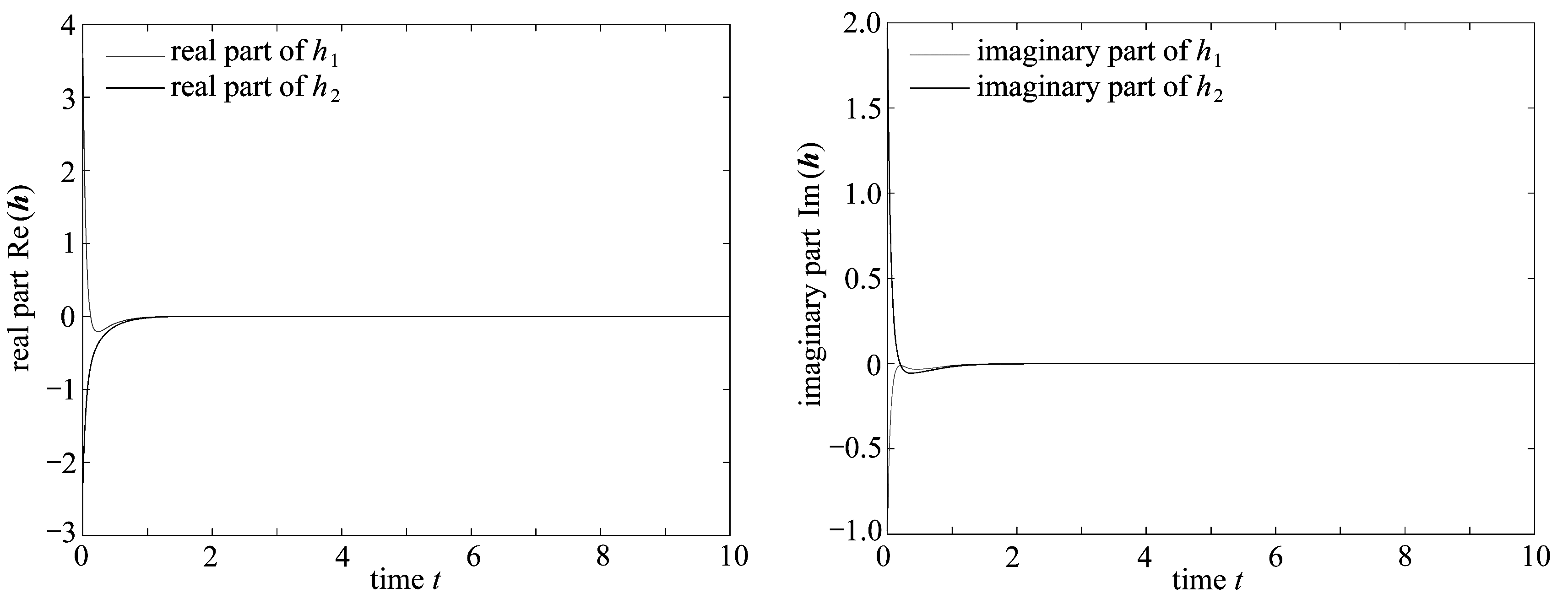
图2 误差状态模型(5)的实部、虚部状态轨迹
Fig. 2 State trajectories of real and imaginary parts of neuronal state h(t) for system(5)
4 结 论
本文研究了具有泄漏时滞、加性离散时变时滞、加性分布时变时滞复数神经网络的状态估计问题.在不要求复数神经网络分解为两个实数神经网络的条件下, 给出了保证误差神经网络状态模型的全局渐近稳定性的充分性判据.同时, 本文所考虑的时变时滞可以是不可微分的.最后, 通过一个数值仿真算例验证了理论分析的有效性.笔者后续将研究具有加性时变时滞的分数阶复数神经网络以及四元数神经网络的相关动力学.
[1] HIROSE A. Dynamics of fully complex-valued neural networks[J]. Electronics Letters, 1992, 28(16): 1492-1494.
[2] LEE D L. Relaxation of the stability condition of the complex-valued neural networks[J]. IEEE Transactions on Neural Networks, 2001, 12(5): 1260-1262.
[3] 张磊, 宋乾坤. 带有比例时滞的复值神经网络全局指数稳定性[J]. 应用数学和力学, 2018, 39(5): 584-591.(ZHANG Lei, SONG Qiankun. Global exponential stability of complex-valued neural networks with proportional delays[J]. Applied Mathematics and Mechanics, 2018, 39(5): 584-591.(in Chinese))
[4] NITTA T. An analysis of the fundamental structure of complex-valued neurons[J]. Neural Processing Letters, 2000, 12(3): 239-246.
[5] ZHOU W, ZURADA J M. Discrete-time recurrent neural networks with complex-valued linear threshold neurons[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2009, 56(8): 669-673.
[6] JANKOWSKI S, LOZOWSKI A, ZURADA J M. Complex-valued multistate neural associative memory[J]. IEEE Transactions on Neural Networks, 1996, 7(6): 1491-1496.
[7] LIU X W, CHEN T P. Global exponential stability for complex-valued recurrent neural networks with asynchronous time delays[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(3): 593-606.
[8] 曹进德, 林怡平. 一类时滞神经网络模型的稳定性[J]. 应用数学和力学, 1999, 20(8): 851-855.(CAO Jinde, LIN Yiping. Stability of a class of neural network models with delay[J]. Applied Mathematics and Mechanics, 1999, 20(8): 851-855.(in Chinese))
[9] BAI X Z, WANG Z D, ZOU L, et al. Target tracking for wireless localization systems with degraded measurements and quantization effects[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9687-9697.
[10] WANG F, WANG Z D, LIANG J L, et al. Resilient filtering for linear time-varying repetitive processes under uniform quantizations and round-robin protocols[J]. IEEE Transactions on Circutts and Systems Ⅰ: Regular Papers, 2018, 65(9): 2992-3004.
[11] CHEN X F, ZHAO Z J, SONG Q K, et al. Multistability of complex-valued neural networks with time-varying delays[J]. Applied Mathematics and Computation, 2017, 294: 18-35.
[12] HANG H, WANG X Y, LIN X H. Synchronization of complex-valued neural network with sliding mode control[J]. Journal of the Franklin Institute, 2016, 353(2): 345-358.
[13] LIU Y R, WANG Z D, LIU X H. Global asymptotic stability of generalized bi-directional associative memory networks with discrete and distributed delays[J]. Chaos, Solitons and Fractals, 2006, 28(3): 793-803.
[14] LAM J, GAO H, WANG C. Stability analysis for continuous systems with two additive time-varying delay components[J]. Systems and Control Letters, 2007, 56(1): 16-24.
[15] CHEN X F, SONG Q K. State estimation for quaternion-valued neural networks with multiple time delays[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017. DOI: 10.1109/TSMC.2017.2776940.
[16] 曾德强, 吴开腾, 宋乾坤, 等. 时滞神经网络随机抽样控制的状态估计[J]. 应用数学和力学, 2018, 39(7): 821-832.(ZENG Deqiang, WU Kaiteng, SONG Qiankun, et al. State estimation for delayed neural networks with stochastic sampled-data control[J]. Applied Mathematics and Mechanics, 2018, 39(7): 821-832.(in Chinese))
[17] HUANG H, FENG G, CAO J D. Robust state estimation for uncertain neural networks with time-varying delay[J]. IEEE Transactions on Neural Networks, 2008, 19(8): 1329-1339.
[18] WANG H W, SONG Q K. State estimation for neural networks with mixed interval time-varying delays[J]. Neurocomputing, 2010, 73(7/9): 1281-1288.
[19] WU Z G, SHI P, SU H Y, et al. State estimation for discrete-time neural networks with time-varying delay[J]. International Journal of Systems Science, 2012, 43(4): 647-655.
[20] YAN L, ZHANG S J, DING D R, et al. H∞ state estimation for memristive neural networks with multiple fading measurements[J]. Neurocomputing, 2017, 230: 23-29.
[21] LIANG J, LI K L, SONG Q K, et al. State estimation of complex-valued neural networks with two additive time-varying delays[J]. Neurocomputing, 2018, 309: 54-61.