引 言
长期以来,人类健康受到传染病的巨大威胁.为了减缓其对人类威胁,大量的数学模型被建立且用于分析传染病的动力学行为.其中经典的是Kermack和McKendrick[1]对伦敦的黑死病和孟买的瘟疫传播规律的研究.除此以外,关于传染病的研究还有许多著名的模型[1-3],这些模型为我们提供了有用的控制措施.一个由Lahrouz等提出的SIRS模型[4]有以下形式:
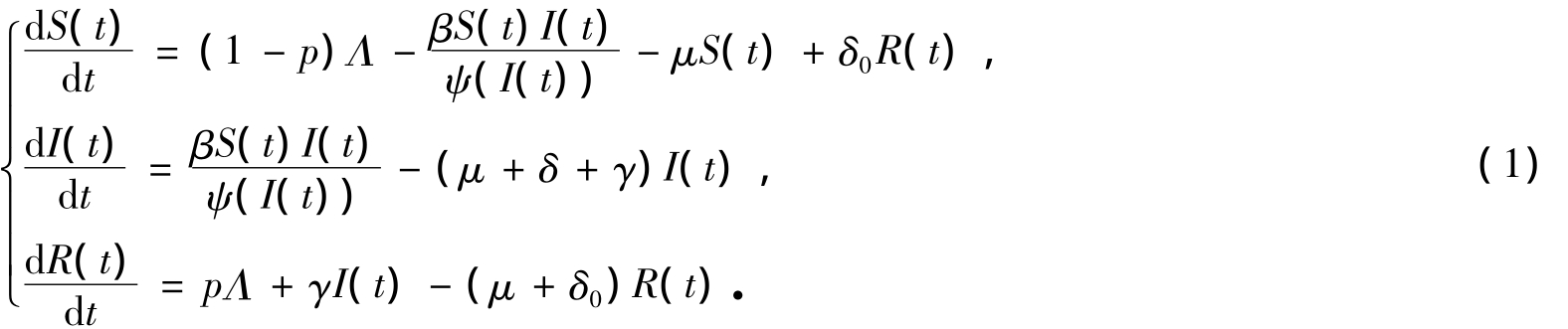
为了更好地控制传染病的传播,除了采取药物管制措施(如接种疫苗和抗病毒药物)以外,还应采取非药物控制措施(包括信息干预)[5-6].在传染病传播初期,由于药物干预措施的缺乏[7-8],因此有必要研究一个非药物控制措施即信息干预对疾病流行影响的模型.Kumar等[6]提出了连续SIRS传染病模型:
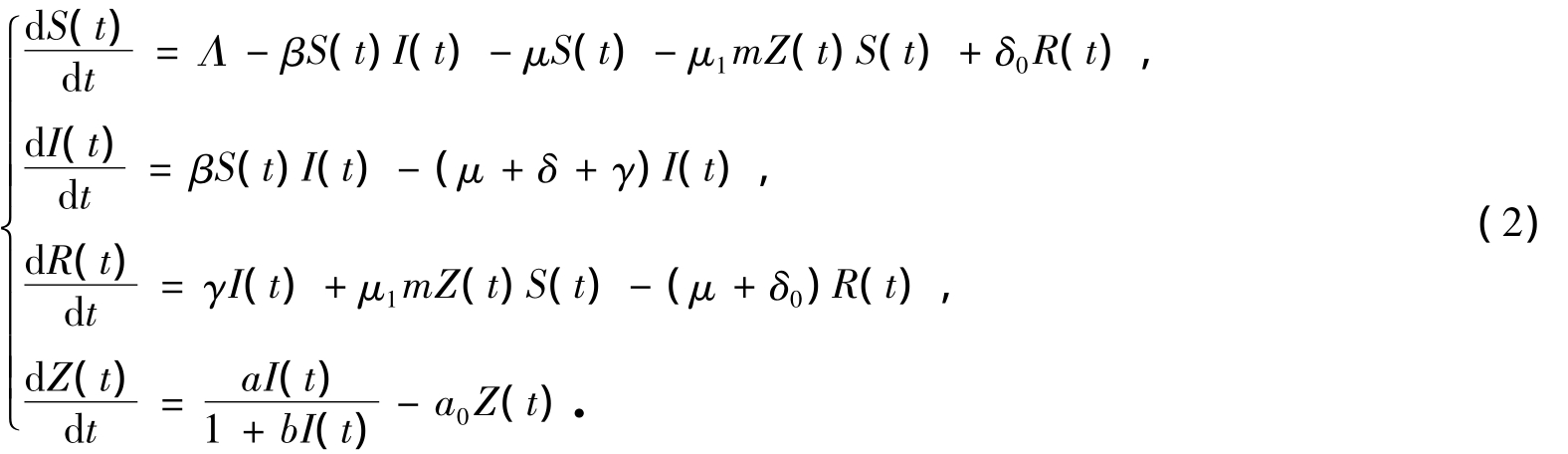
上述两个模型均没有考虑时滞的影响,这是不符合实际的.事实上,流行病的传播具有时滞这一特点,具体包括潜伏期时滞、感染期时滞、失去免疫期时滞等[9-11].Cooke[12]研究了一个带时滞的SIR模型,其中传染率函数为βS(t)I(t-τ),τ是一个固定时间,只有经过这段时间,易感人群才能被感染者感染.该模型如下:
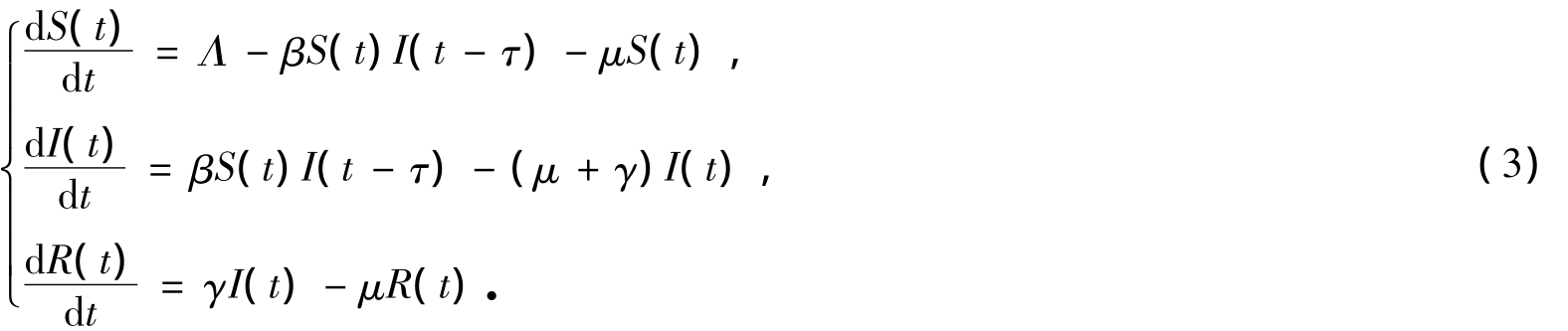
结合这3个模型,得到考虑时滞影响及标准发生率下的SIRS模型:

其中S(t),I(t),R(t)和Z(t)分别代表易感人群、感染人群、恢复人群和信息在t时刻的数量,I(t-τ)代表在t时刻经过潜伏期后处于感染期的感染者数量,τ>0是一定值代表已感染者成为带菌者所需要的时间,N(t)=S(t)+I(t)+R(t),Λ是总人口,其中比例p的人是接种疫苗的,1-p是容易感染的(0≤p≤1),γ是感染人群的恢复率,μ是自然死亡率,δ是疾病引起的死亡率,β是接触传播系数,δ0=δ1+δ2表示失去免疫的总比率,包括失去自然免疫的比率δ1和失去由保障措施所得免疫力的比率δ2,m表示信息交互率,μ1(0≤μ1≤1)代表反应强度,a表示信息的增长速度,b是饱和常数,a0是信息的自然衰减率.所有参数假定非负.
基本再生数[13]是流行病学中的一个重要概念.模型(4)的基本再生数为
模型(4)有两个均衡点[6]:一个是无病平衡点![]() 一个是地方病平衡点E*=(S*,I*,R*,Z*).无病平衡点总是存在,地方病平衡点只有满足R0>1才存在.
一个是地方病平衡点E*=(S*,I*,R*,Z*).无病平衡点总是存在,地方病平衡点只有满足R0>1才存在.
另外,疾病传播中噪声的影响不可忽略[14].因此在模型(4)中考虑μ为随机波动的情形,即考虑Gauss白噪声对模型做了一个扰动.因此式(4)变为以下形式:
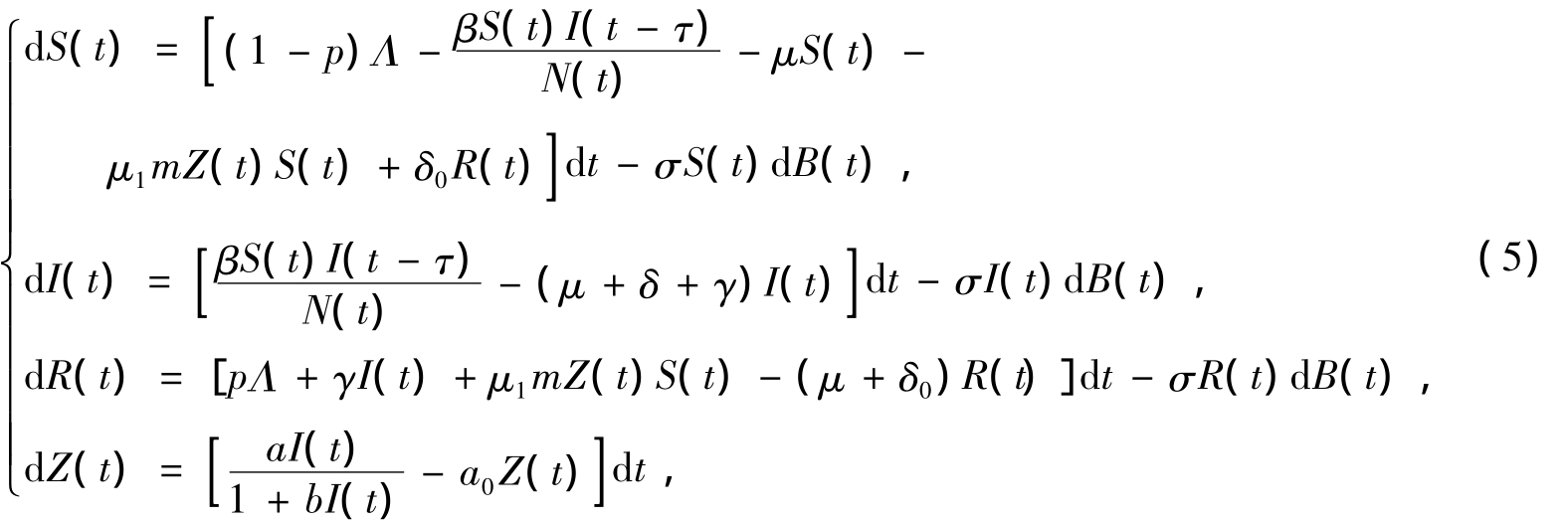
其中B(t)是强度为σ的Brown运动.模型(5)满足初始条件:
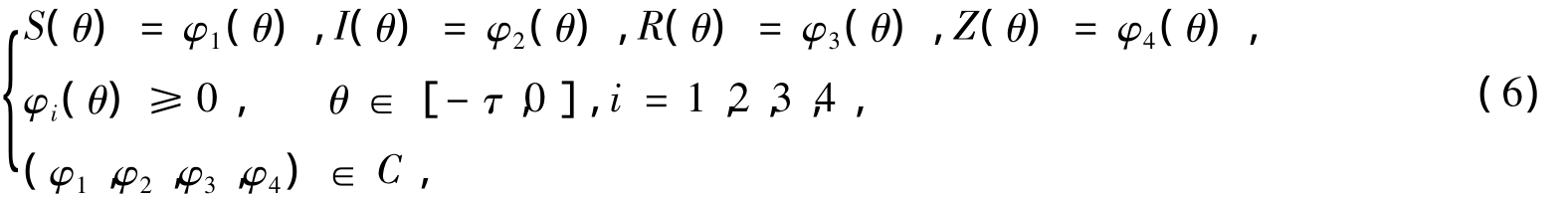
其中C代表Banach空间C([- τ,0];R4+)中从区间[- τ,0]到R4+ = {(x1,x2,x3,x4)xi≥ 0,i=1,2,3,4 } 的连续映射.
模型(5)即为本文所要研究的模型,该模型是结合文献[6]和文献[12]并且采用标准发生率和考虑白噪声的影响提出的.本文研究了模型(5)正解的全局存在性与唯一性和该模型的解在其确定模型无病平衡点和地方病平衡点附近的渐近行为.
1 正解的全局存在性与唯一性
在下面的证明中都有这样的前提:(Ω,F,Ft,P)是 带有滤波 { Ft}t≥0的完备概率空间并且满足通常的条件(即是增函数并且右连续且包含所有概率为0的集合).定义
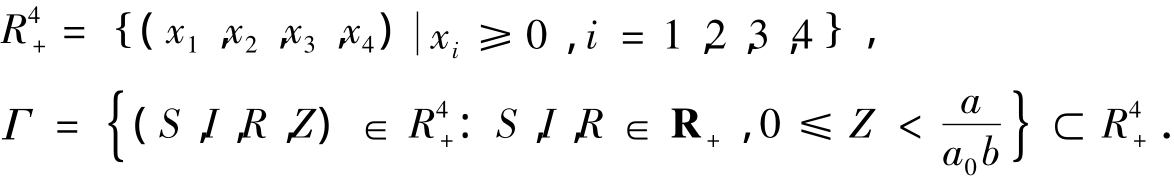
为了了解模型(5)的动力学行为,首先研究解的全局存在性并证明是正解.
定理1 对任意初值(6),模型(5)有唯一全局正解且以概率1保持在R4+上.
证明 因为模型(5)的系数满足局部Lipschitz条件,所以对任意的初值(6)有唯一定义在[- τ,τe)的局部解 (S(t),I(t),R(t),Z(t)),其中 τe为爆炸时间[15].为了证明解是全局的,只需证明几乎肯定τe=∞ .为了证明这一点,设足够大的k0>0使得初值落在区间[1/k0,k0]中.对于每个k≥k0的整数,定义如下的停时:
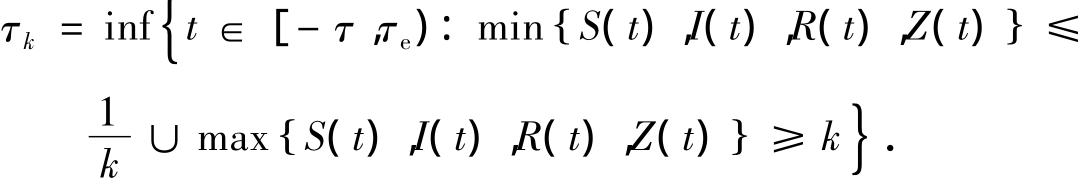
设inf =∞(表示空集).很容易得出当k→∞ 时,τk增加.设τ∞ =limτk,则几乎处处τ∞≤τe.因此,只需证明τ∞ =∞ .假设τ∞≠∞,则存在一个常数T>0和ε∈(0,1)使得 {P τ∞≤ }T >ε,即存在一个整数k1≥k0使得 {P τk≤ }T ≥ε,k≥k1.
定义一个R4+→R+的2阶连续可微函数V:

根据Itô公式有
式中
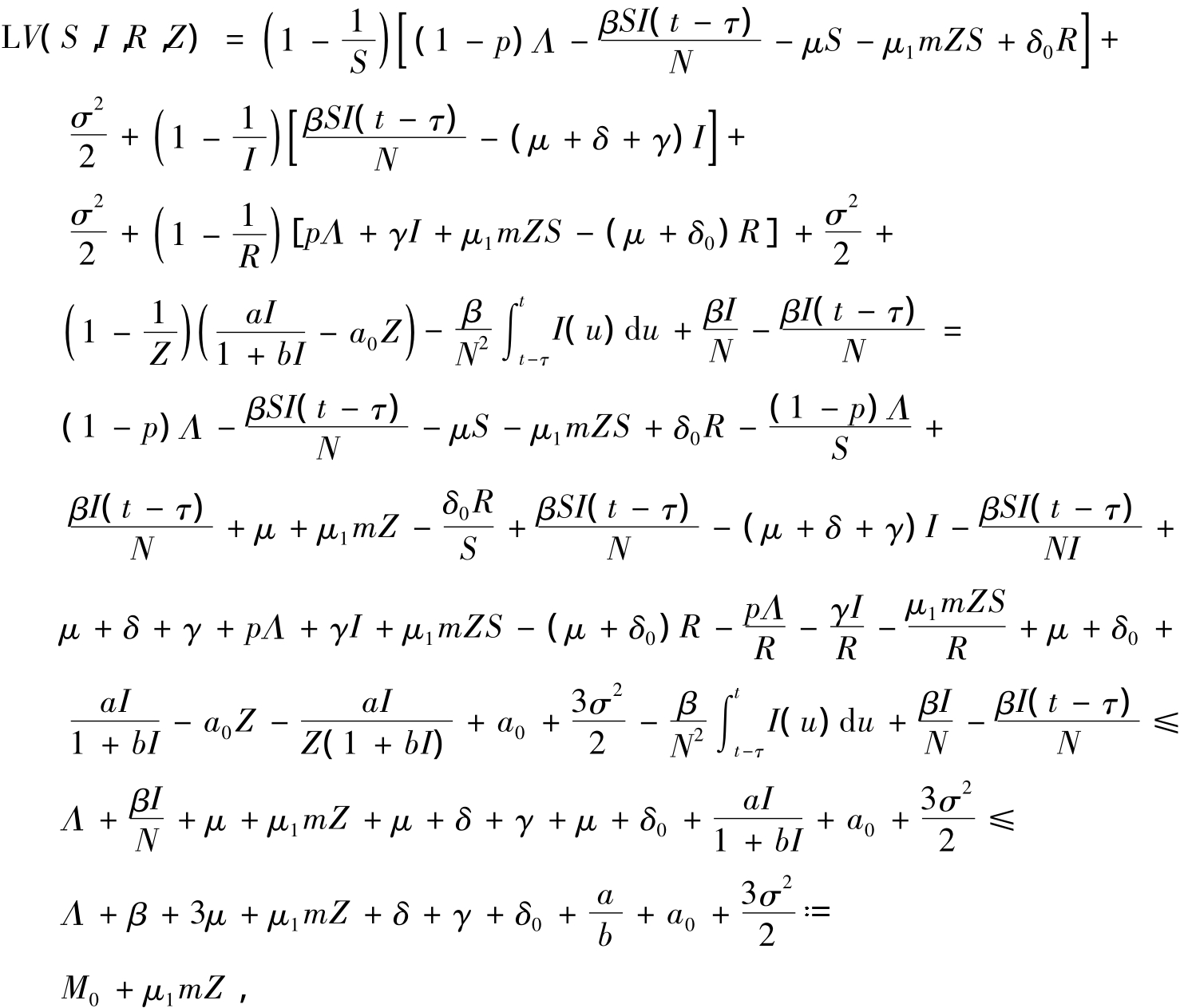
其中
由不等式 Z ≤2(Z -1 - ln Z)+2ln 2≤2V(S,I,R,Z)+2ln 2,有
其中 λ = {max M0+2μ1m ln 2,2μ1 }m ,从而
对式(7)两边同时积分并取期望得
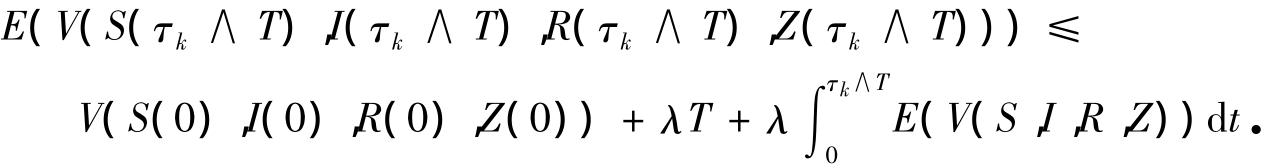
由Gronwall引理,有
设 Ωk {= τk≤ }T ,k≥k1,有P(Ωk)≥ε .注意对每个ω∈Ωk,存在至少一个S(τk,ω),I(τk,ω),R(τk,ω),Z(τk,ω)等于 k或1/k且 V(S(τk),I(τk),R(τk),Z(τk))不少于k -1 - ln k或1/k-1-ln(1/k),即
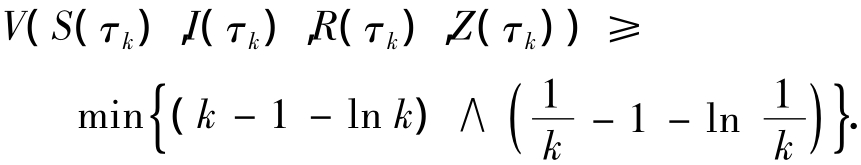
于是可得
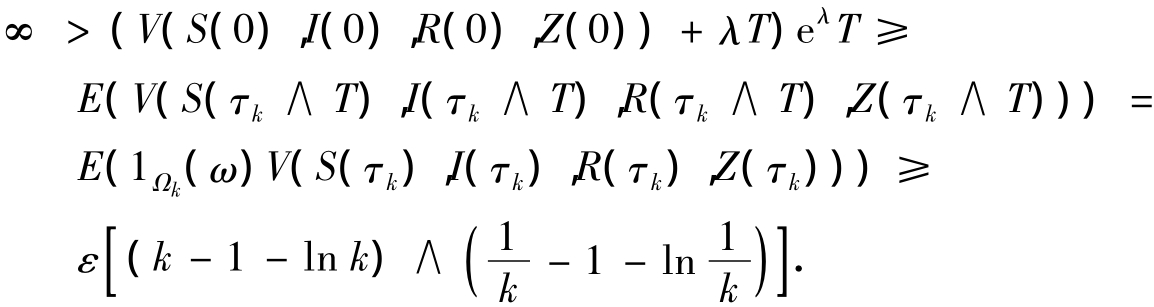
当k→∞ 时有∞ >∞,矛盾,因此有τ∞=∞,得证.
定理2 对任意初值(6),模型(5)有唯一解(S(t),I(t),R(t),Z(t))且以概率1保持在Γ上.
证明 由模型(5)知
根据比较定理[16]有Z <a/a0 b,得证.
2 随机模型的解围绕确定性模型无病平衡点的渐近行为
模型(4)存在无病平衡点![]() (5)的平衡点.下面证明在一定条件下,模型(5)的解围绕E0做随机振动.
(5)的平衡点.下面证明在一定条件下,模型(5)的解围绕E0做随机振动.
将模型(5)的前三个方程相加,得到N(t)满足如下的微分方程:
用变量 (N,I,R,Z)代替 (S,I,R,Z),得到如下的微分方程组:
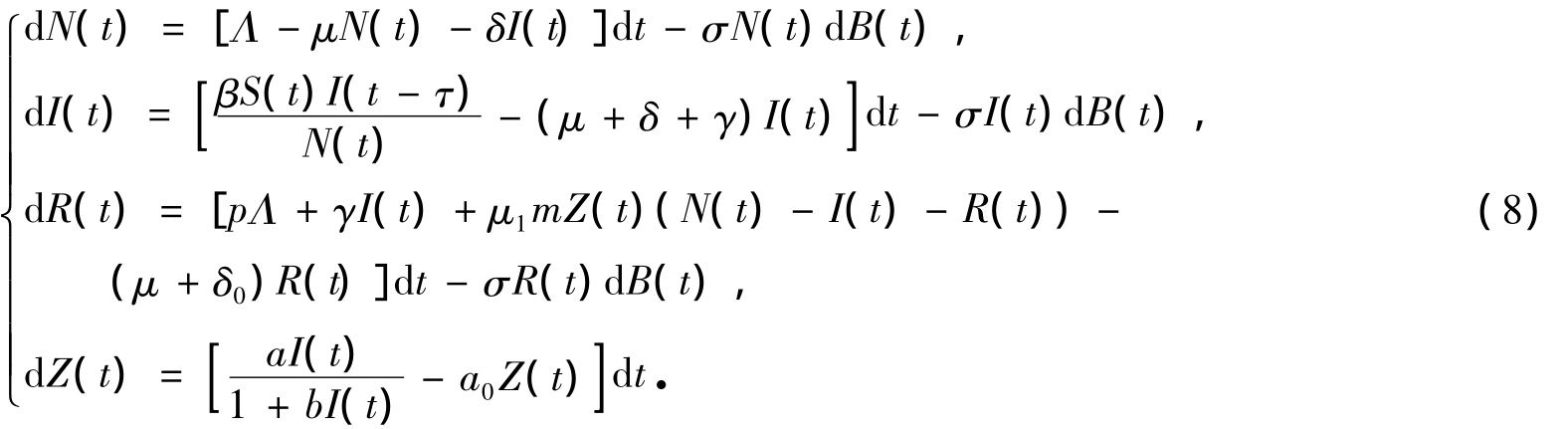
模型(8)确定方程的无病平衡点为![]() 的渐近行为转化为研究模型(8)在无病平衡点E1的渐近行为.
的渐近行为转化为研究模型(8)在无病平衡点E1的渐近行为.
定理3 若模型(8)满足
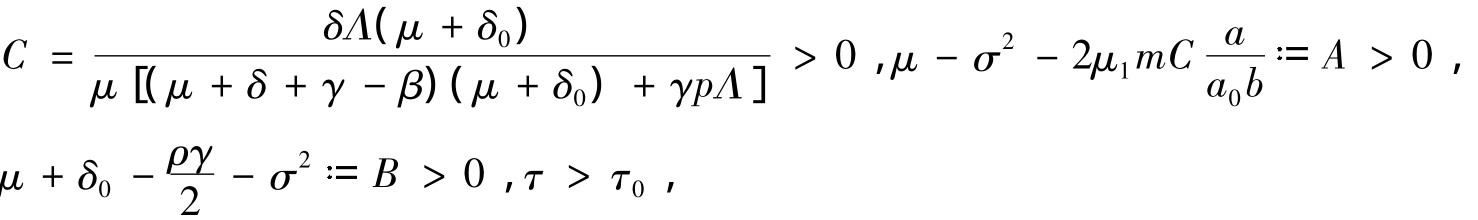
则对任意给定的初值,模型(8)的解具有如下性质:
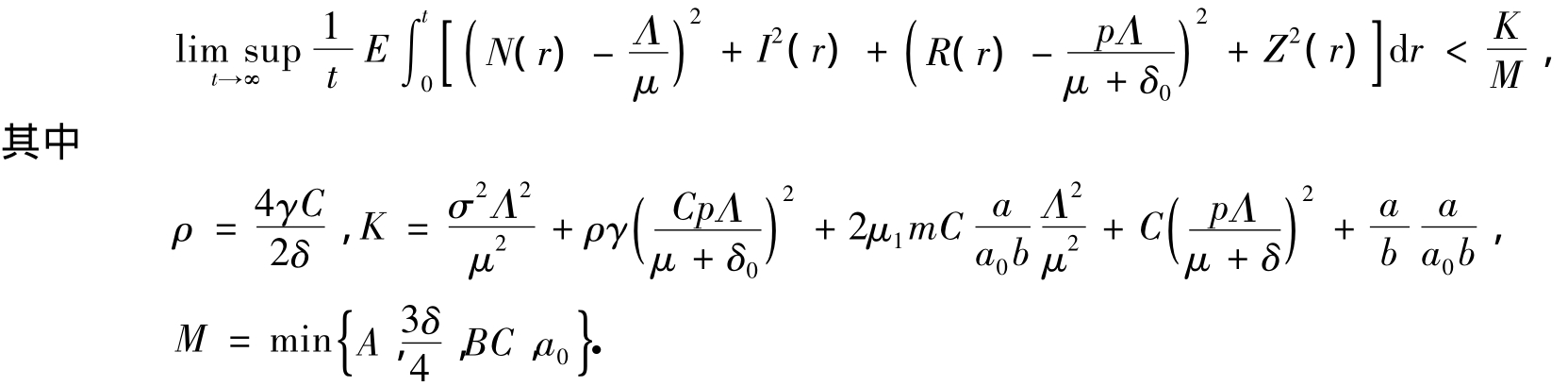
证明 定义一个2阶连续可微函数V1:
根据Itô公式有
其中
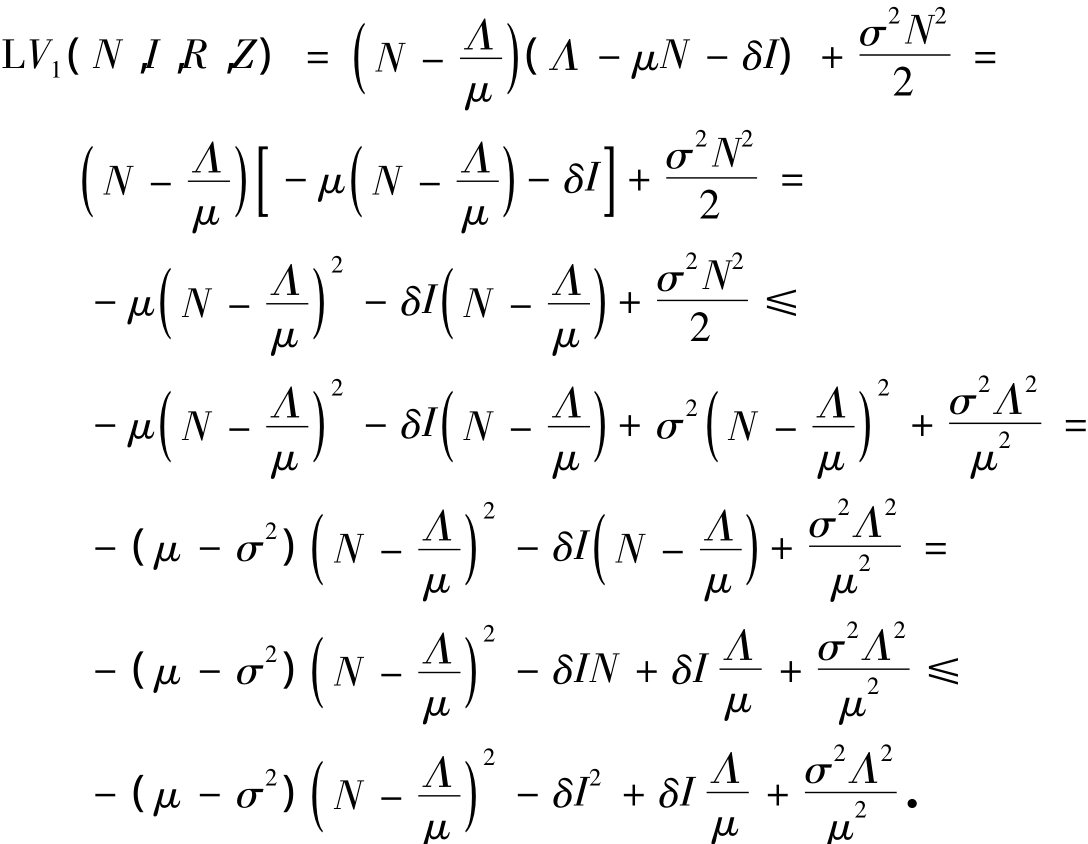
在上述不等式中,我们运用了不等式对a,b∈R有(a+b)2≤2a2+2b2.
定义一个2阶连续可微函数V2:
根据Itô公式有
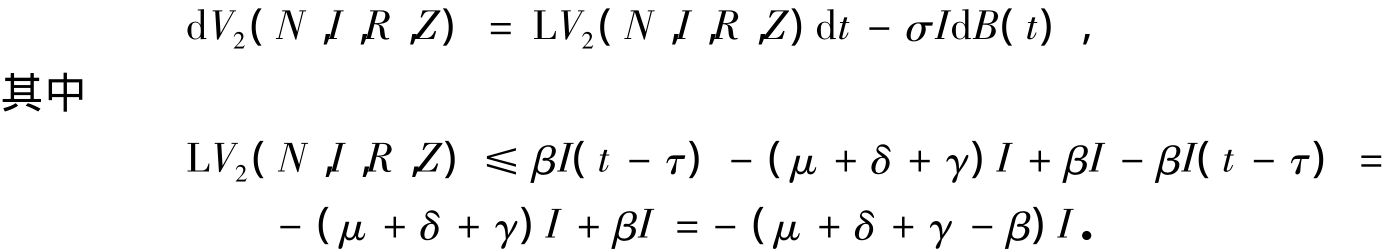
定义一个2阶连续可微函数V3:
根据Itô公式有
其中

在上述不等式中,我们运用了不等式对a,b∈R有(a+b)2≤2a2+2b2和-ρ∈R+使得
定义一个2阶连续可微函数V4:
则
定义一个2阶连续可微函数V:
其中C∈R+.根据Itô公式有
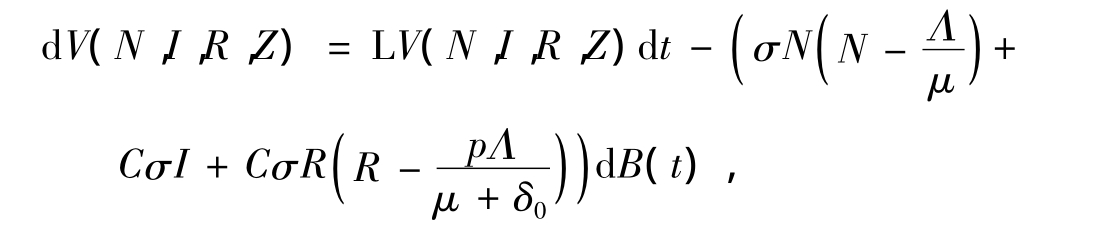
其中
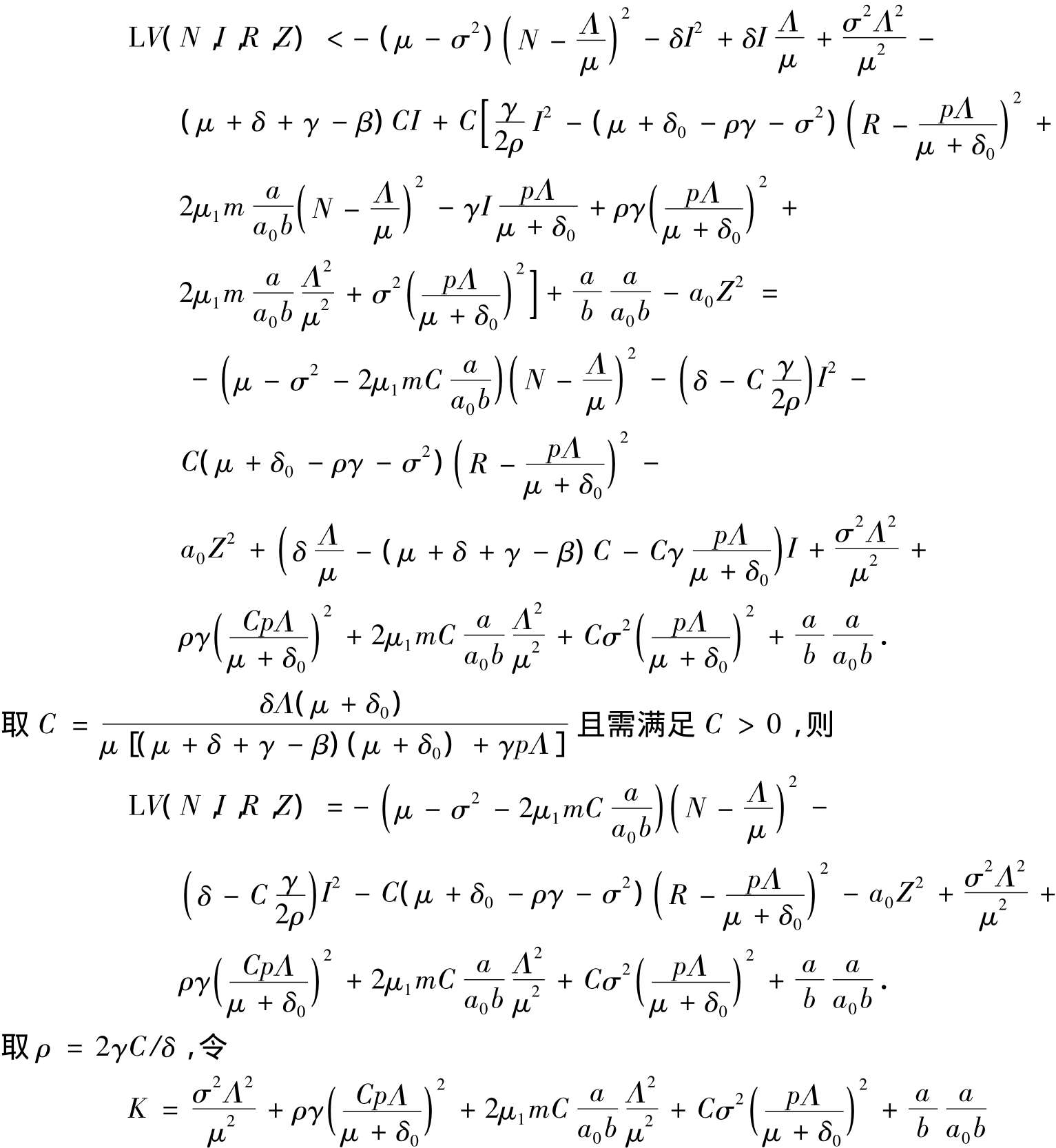
且满足
则
对d V两端从0到t积分并取期望有
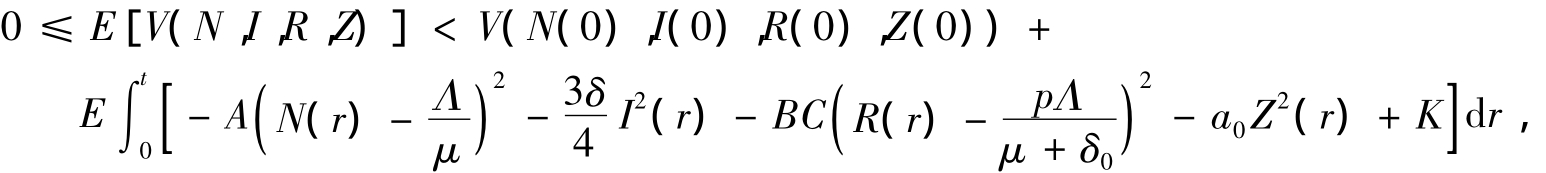
也即
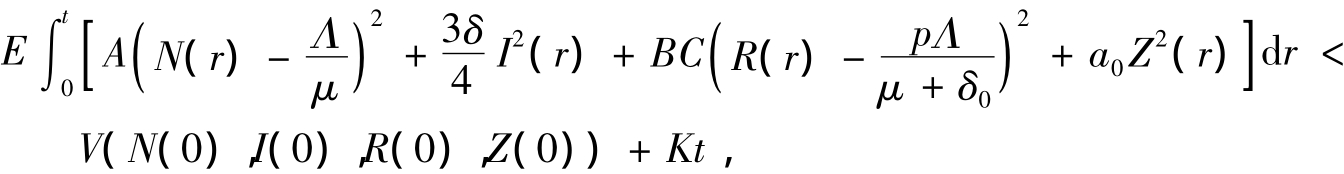
所以有

证毕.
由于模型(8)在无病平衡点E1的渐近行为与模型(5)在无病平衡点E0的渐近行为等价,所以侧面证明了模型(5)在无病平衡点E0的渐近行为.
注1 定理3表明:模型(8)的解围绕无病平衡点E1做随机振动,振动的强度与σ2有关,σ2的值越小,振动越弱,即随机干扰越小,模型(8)的解越接近确定性SIRS模型的无病平衡点E1,从而侧面证明了模型(5)的解越接近确定性SIRS模型的无病平衡点E0,此时,疾病会消失.
3 随机模型的解围绕确定性模型地方病平衡点的渐近行为
若R0>1,模型(4)存在地方病平衡点E*=(S*,I*,R*,Z*),但是该平衡点不是模型(5)的平衡点.下面证明在一定条件下,模型(5)的解围绕E*做随机振动.
定理4 若模型(5)满足
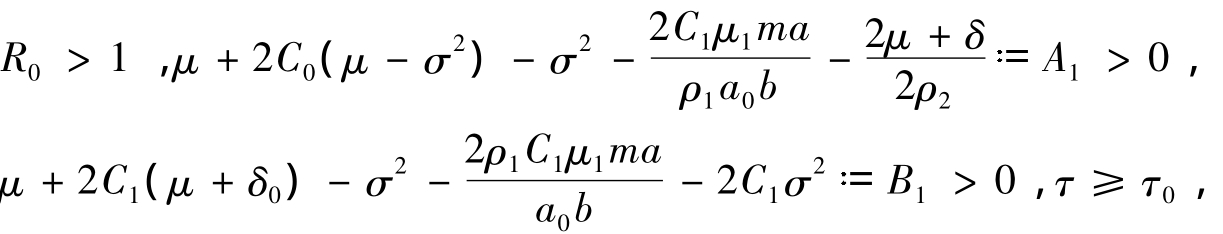
则对任意给定的初值(6),模型(5)的解具有如下性质:

其中
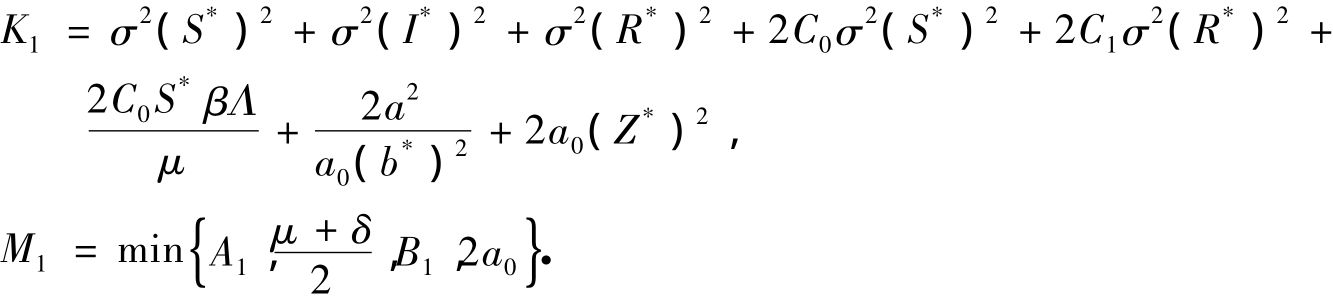
证明 定义一个2阶连续可微函数V1:
根据Itô公式有
其中
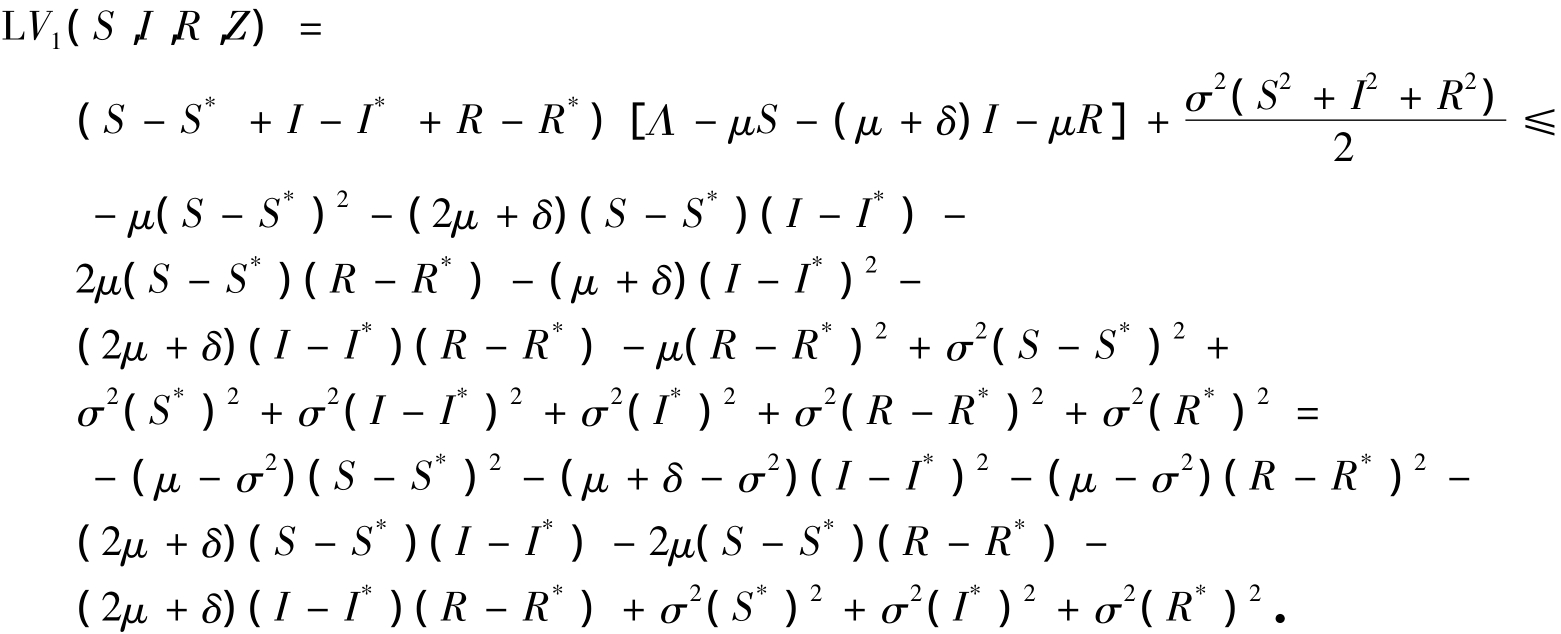
在上述不等式中,我们运用了不等式对a,b∈R有(a+b)2≤2a2+2b2.
定义一个2阶连续可微函数V2:
根据Itô公式有
其中
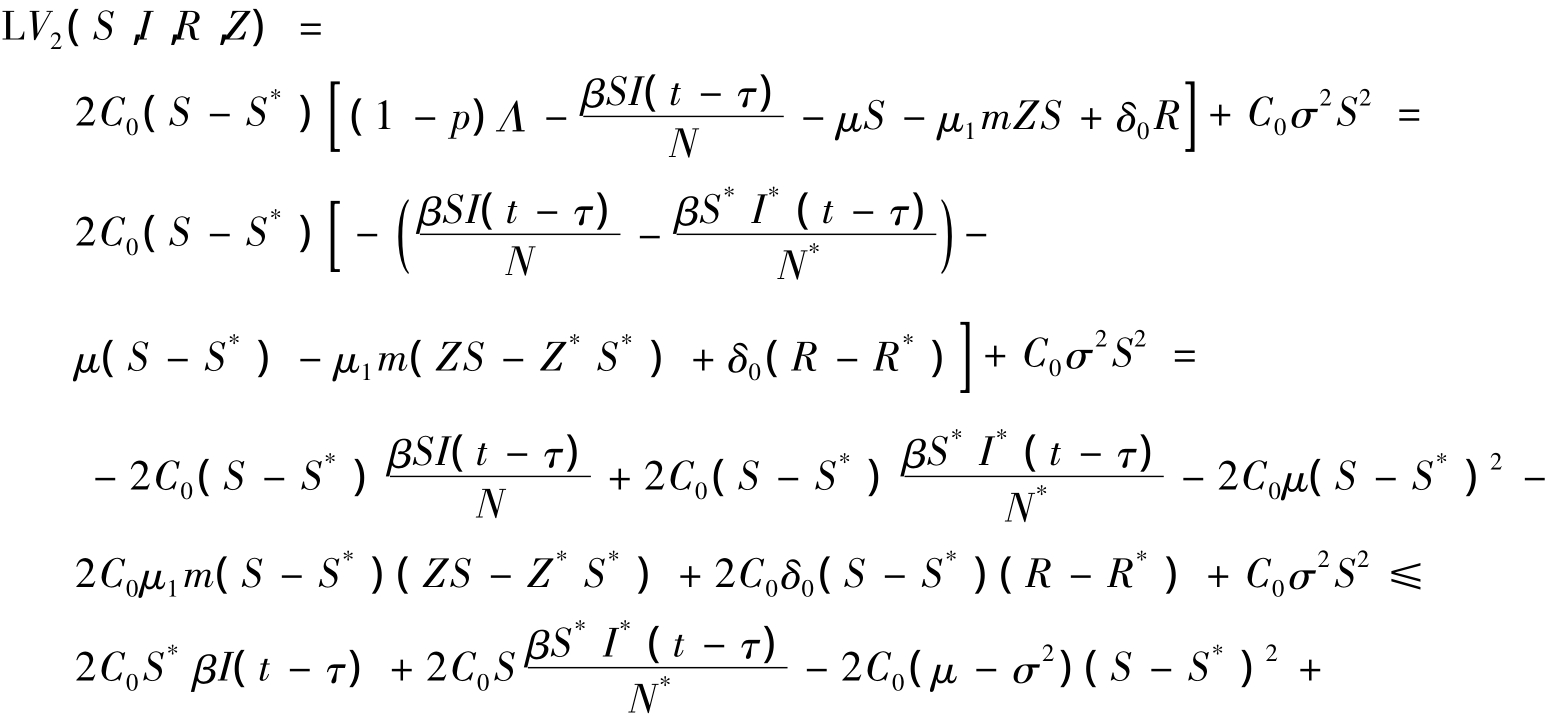
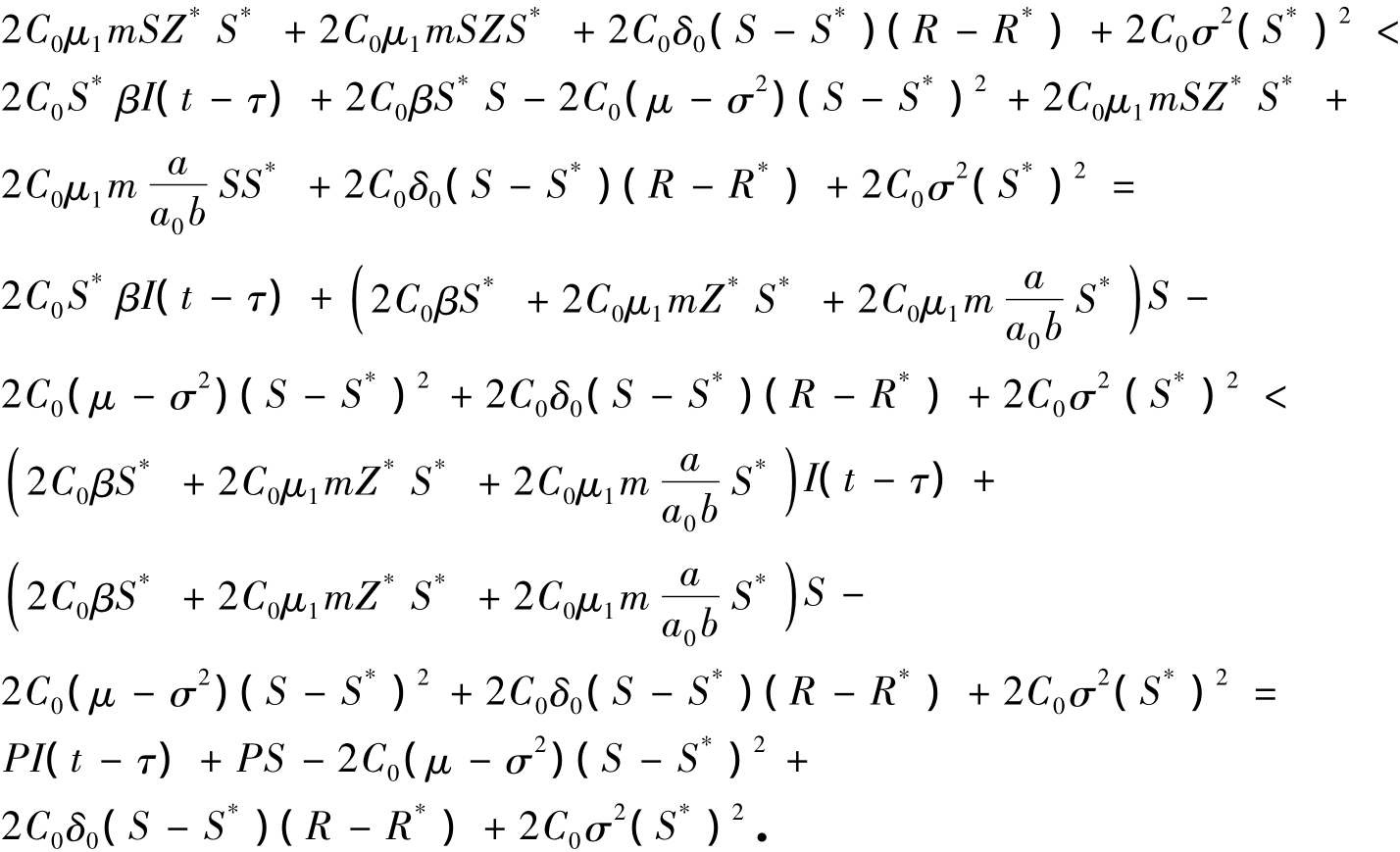
在上述不等式中,我们定义
且运用了不等式对a,b∈R有(a+b)2≤2a2+2b2.
定义一个2阶连续可微函数V3:
根据Itô公式有
其中
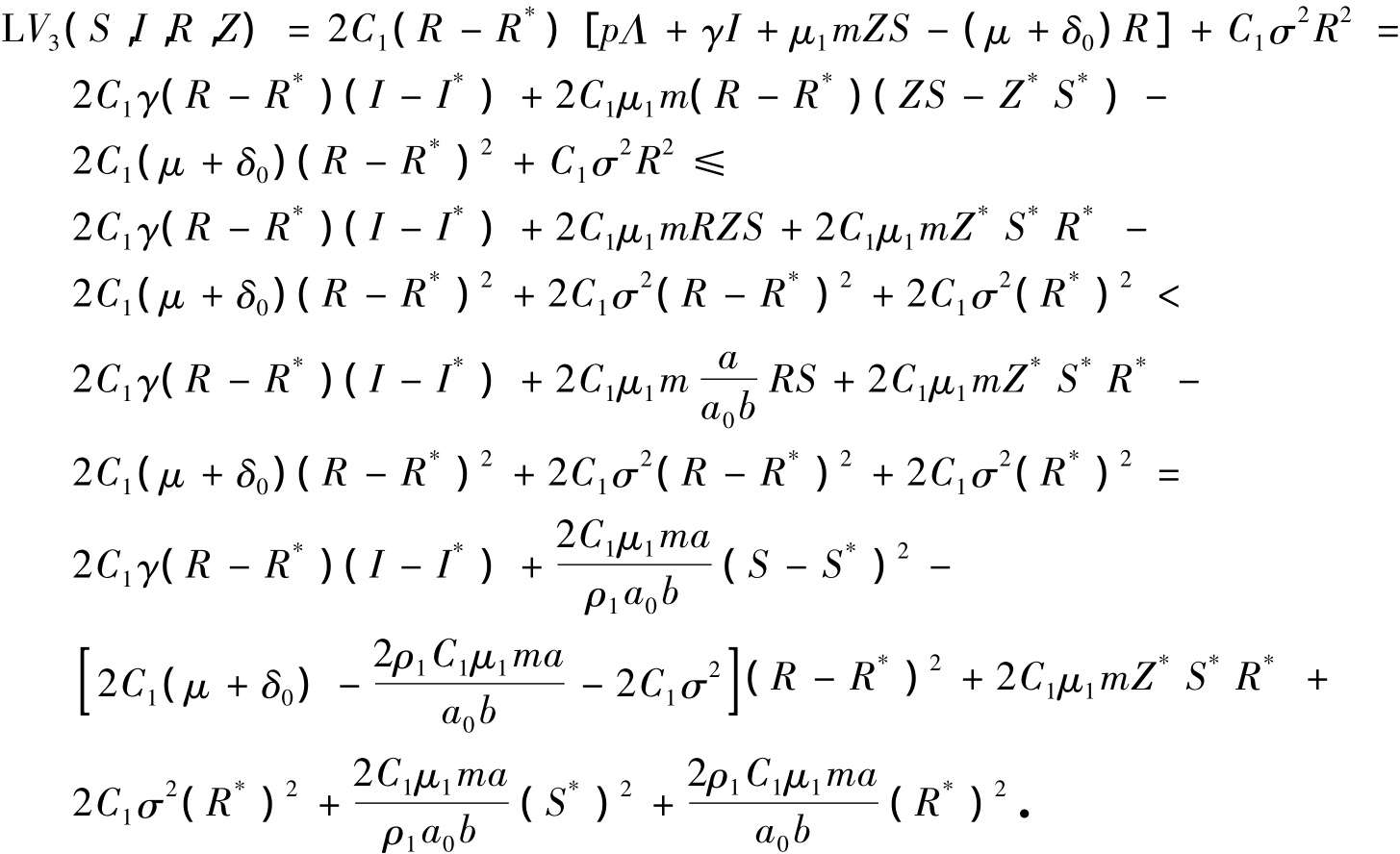
在上述不等式中,我们运用了不等式对a,b∈R有(a+b)2≤2a2+2b2和-ρ1∈R+使得
定义一个2阶连续可微函数V4:
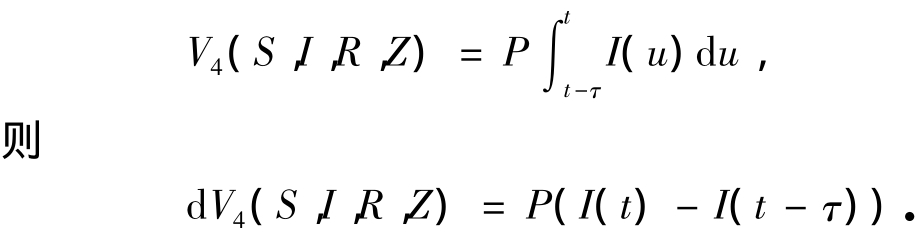
定义一个2阶连续可微函数V5:
根据Itô公式有
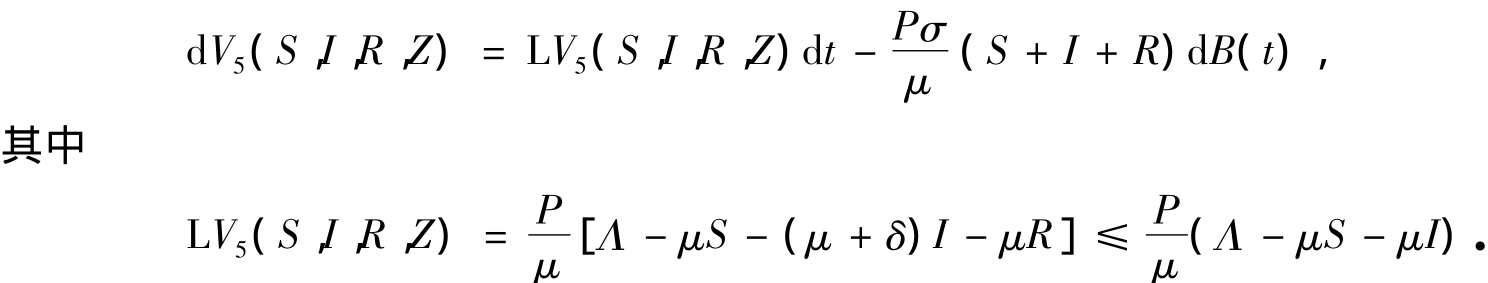
定义一个2阶连续可微函数V6:
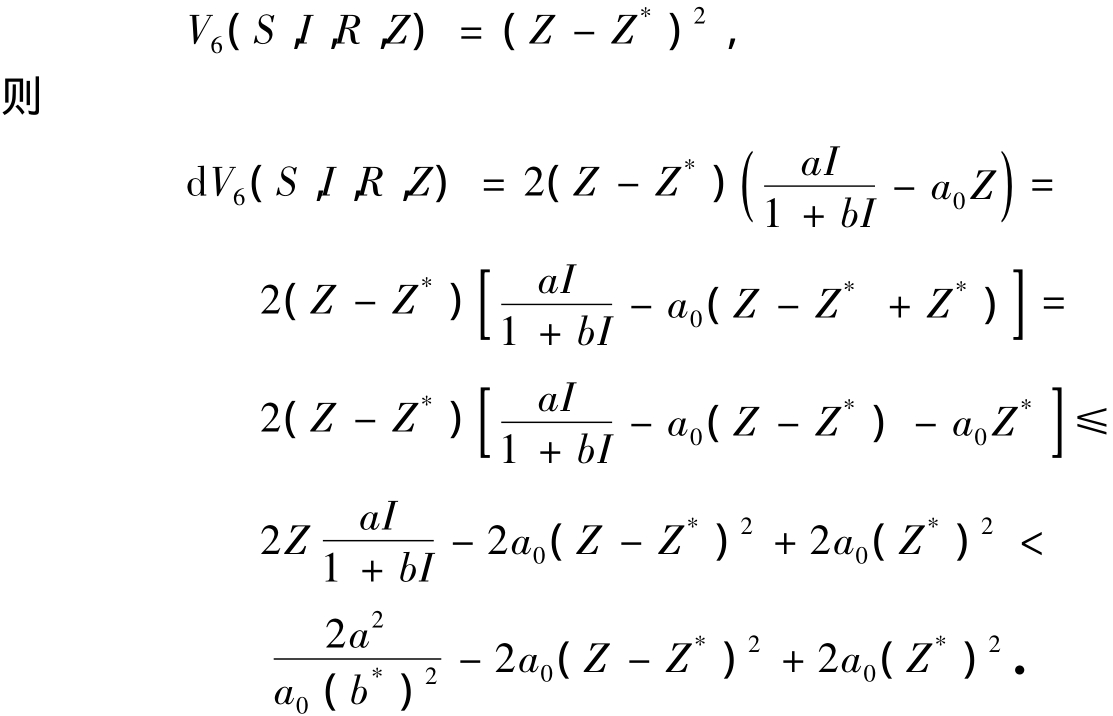
定义一个2阶连续可微函数V:
根据Itô公式有
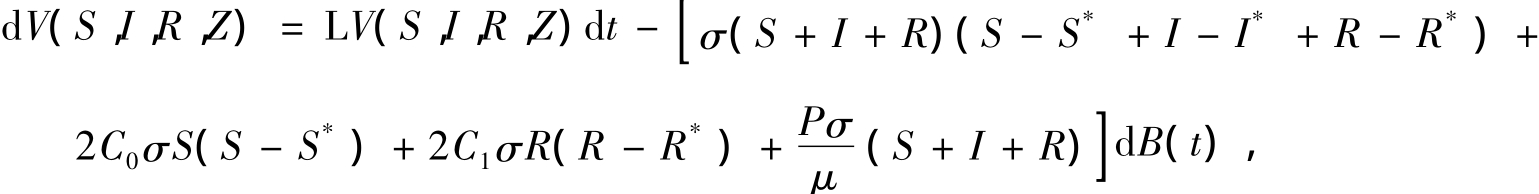
其中
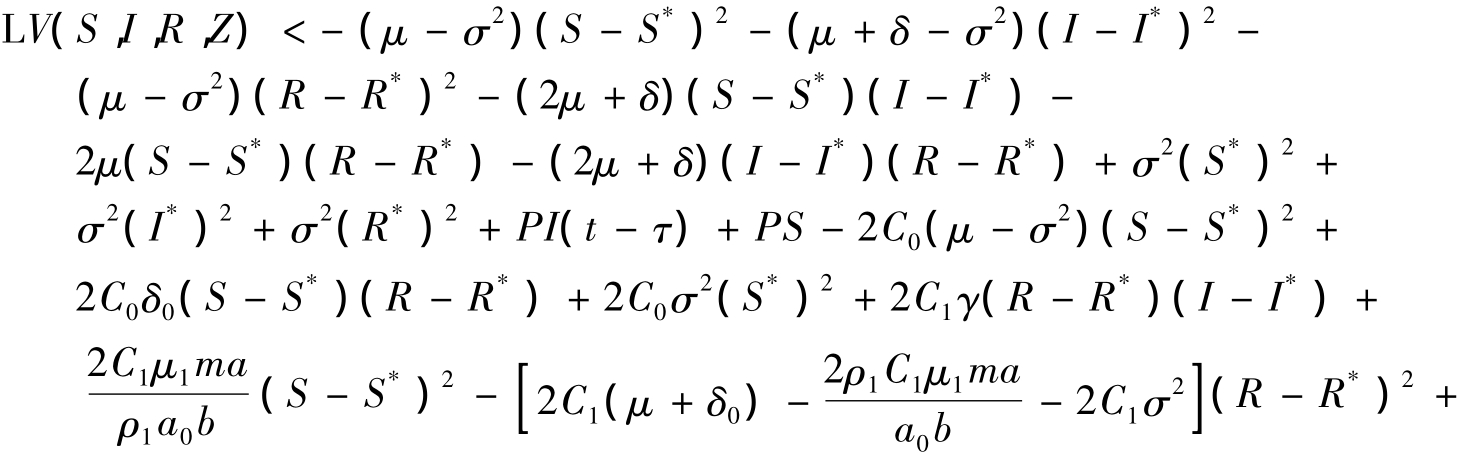

取 C0= μ/δ0,C1=(2μ + δ)/2γ,则
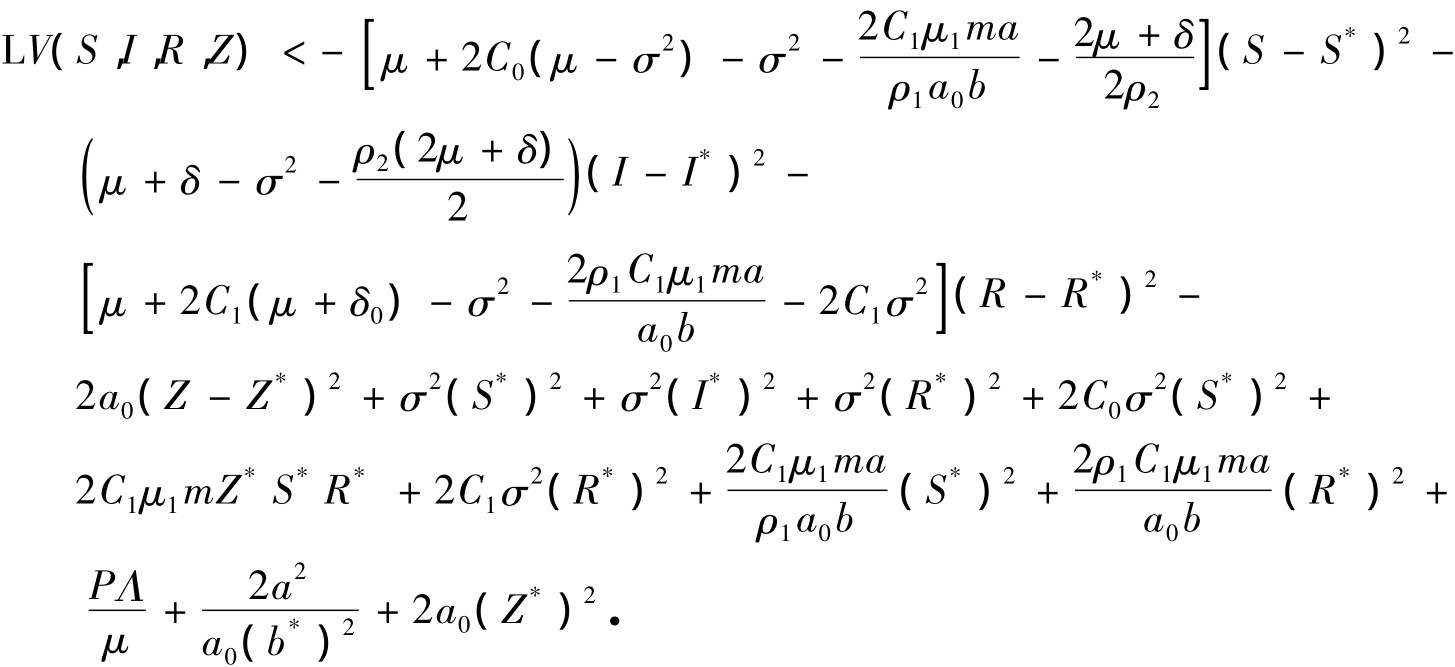
在上述不等式中,我们运用了不等式-ρ2∈R+使得
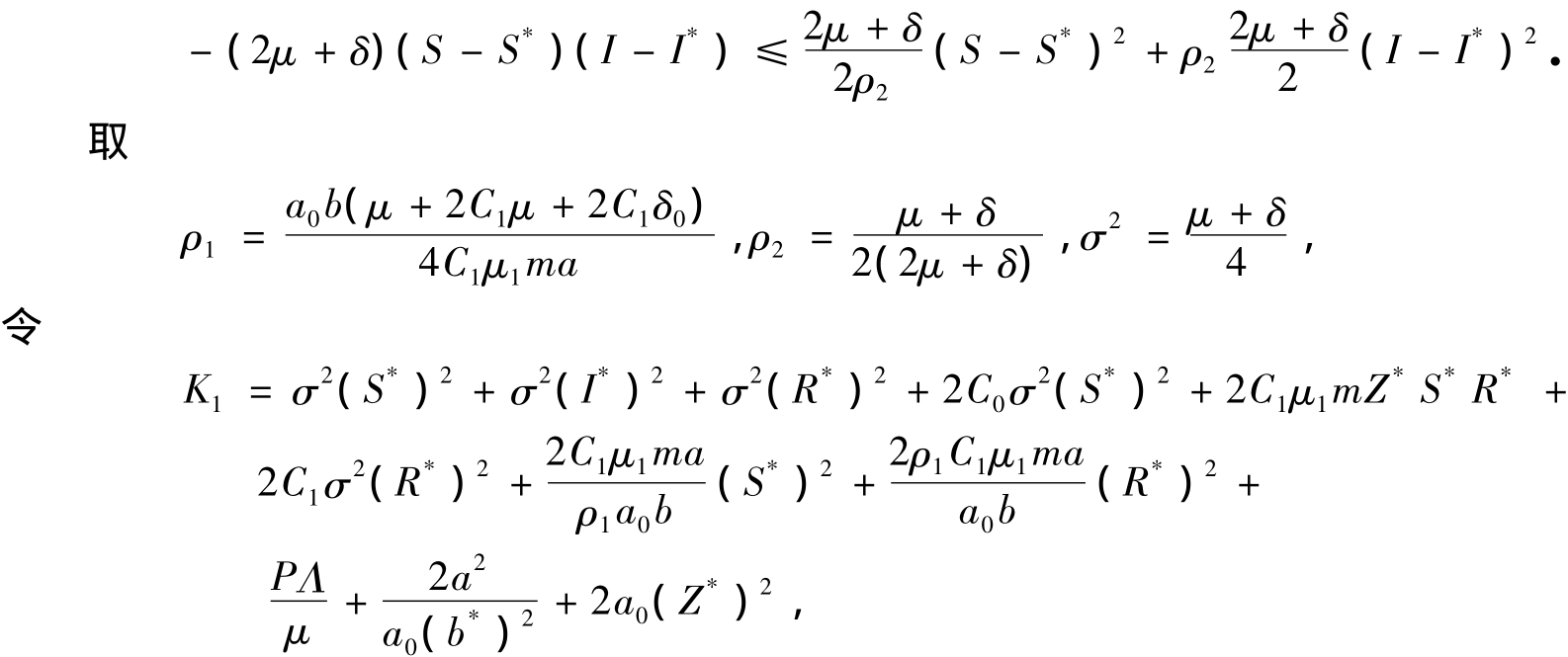
且满足
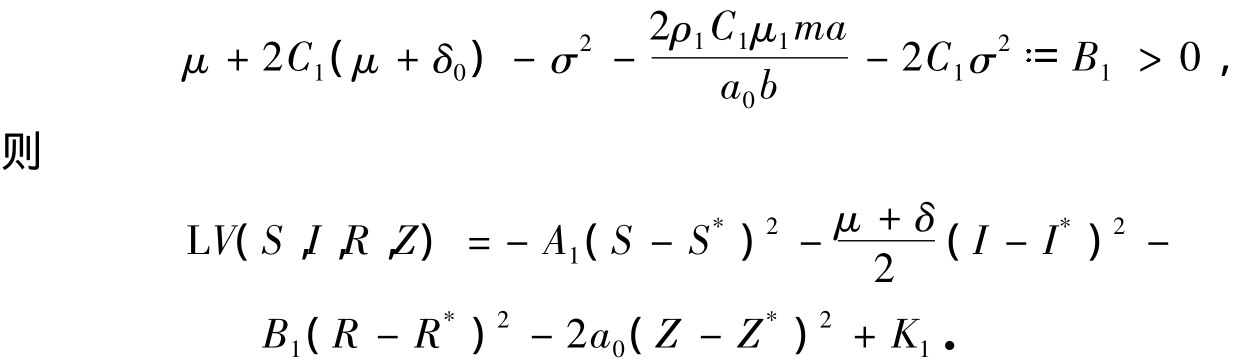
对d V两端从0到t积分并取期望有
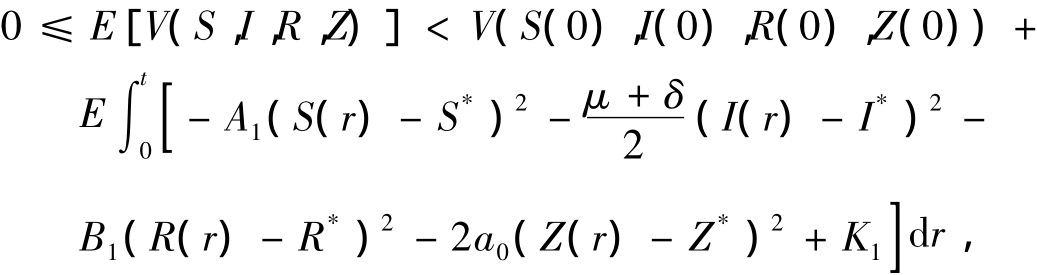
也即
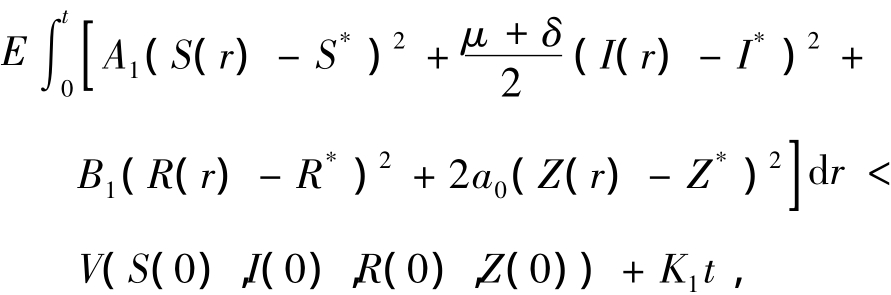
所以有
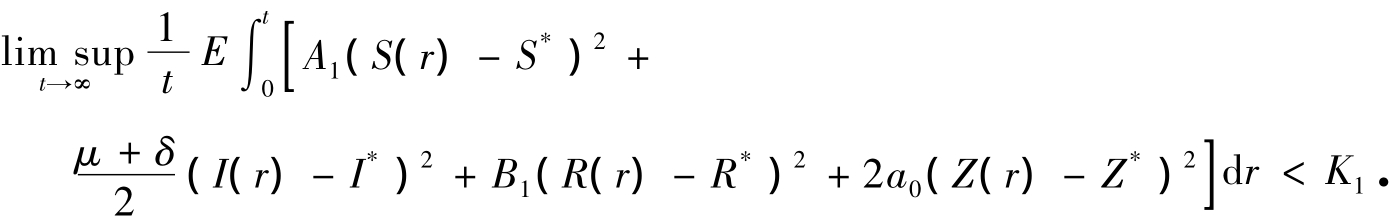
令
由已知条件可知M1>0,使得
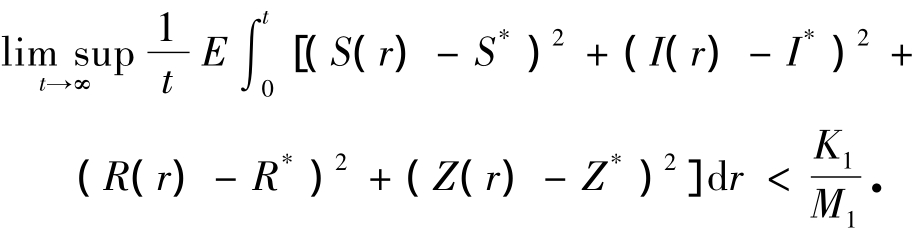
证毕.
注2 定理4表明:模型(5)的解围绕地方病平衡点E*做随机振动,振动的强度与σ2有关,σ2的值越小,振动越弱,即随机干扰越小,模型(5)的解越接近确定性SIRS模型的地方病平衡点E*,此时,疾病将会持续.
4 结论与展望
本文考虑了一类带有标准发生率和信息干预的随机时滞SIRS传染病模型,研究了模型唯一正解的全局存在性和该模型的解在其确定模型无病平衡点和地方病平衡点附近的渐近行为,得到了在一定条件下模型(5)的解分别围绕无病平衡点E0和地方病平衡点E*做随机振动.振动的强度与σ2有关,σ2的值越小,振动越弱,即随机干扰越小,模型(5)的解分别越接近确定性SIRS模型的无病平衡点E0和地方病平衡点E*.文章有一些新的问题有待解决,如在现实生活中,不同年龄的人群对流行病的抵抗能力有着较大的差异,将年龄结构引入到模型中,是后期的一个研究方向.
[1] KERMACK WO,MCKENDRICK A G.Contributions to the mathematical theory of epidemics:Ⅰ[J].Bulletin of Mathematical Biology,1991,53(1):33-55.
[2] MA Z E,ZHOU Y C,WU J H.Modeling and Dynamics of Infectious Diseases[M].Beijing:Higher Education Press,2009.
[3] LIU Q,CHEN Q.Analysis of the deterministic and stochastic SIRSepidemic models with nonlinear incidence[J].Physica A:Statistical Mechanics and Itôs Applications,2015,428(1):140-153.
[4] LAHROUZ A,OMARI L,KIOUACH D,et al.Complete global stability foran SIRS epidemic model with generalized non-linear incidence and vaccination[J].Applied Mathematics and Computation,2012,218(1):6519-6525.
[5] UN I W,JANN T W,SHAN C C,et al.Impacts of a mass vaccination campaign against pandemic H1N1 2009 influenza in Taiwan:a time-series regression analysis[J].International Journal of Infectious Diseases,2014,23:82-89.
[6] KUMAR A,SRIVASTAVA P K,TAKEUCHI Y.Modeling the role of information and limited optimal treatment on disease prevalence[J].Journal of Theoretical Biology,2017,414(1):103-119.
[7] PAINTER J E,DICLEMENTE R J,VON FRICKEN M E.Interest in an Ebola vaccine among a US national sample during the height of the 2014—2016 Ebola outbreak in West Africa[J].Vaccine,2017,35(4):508-512.
[8] SHIWANI H A,PHARITHI R B,KHAN B,et al.An update on the 2014 Ebola outbreak in West Africa[J].Asian Pacific Journal of Tropical Medicine,2017,10(1):6-10.
[9] ZHANG T L,LIU J L,TENG Z D.Stability of Hopf bifurcation of a delayed SIRS epidemic model with stage structure[J].Nonlinear Analysis:Real World Applications,2010,11(1):293-306.
[10] ZHANG F P,LIZ Z,ZHANG F.Global stability of an SIR epidemic model with constant infectious period[J].Applied Mathematics and Computation,2008,199(1):285-291.
[11] QI L X,CUI J A.The stability of an SEIRSmodel with nonlinear incidence,vertical transmission and time delay[J].Applied Mathematics and Computation,2013,221(1):360-366.
[12] COOKE K L.Stability analysis fora vectordisease model[J].Rocky Mountain Journal of Mathematics,1979,9(1).DOI:10.1216/RMJ-1979-9-1-31.
[13] HEFFERNAN J M,SMITH R J,WAHL L M.Perspectives on the basic reproductive ratio[J].Journal of the Royal Society Interface,2005,2(4):281-293.
[14] CAI Y,KANG Y,BANERJEE M,et al.A stochastic SIRS epidemic model with infectious force under intervention strategies[J].Journal of Differential Equations,2015,259(12):7463-7502.
[15] MAO X R.Stochastic Differential Equations and Applications[M].Chichester:Horwood Publishing Limited,1997.
[16] IKEDA N,WATANABE S.Stochastic Differential Equations and Diffusion Processes[M].New York:North-Holland,1981.