引 言
机械、车辆、桥梁、房屋建筑等工程常处于复杂动载荷激励状态下,只有准确获得这些复杂的动载荷信息,才能判断工程结构的安全可靠性.然而在众多实际工程中,如闸门所受的水动力载荷、汽车驶过桥梁时桥梁所受的激振力、地震时房屋结构所受的地震力,由于这些动载荷常处于复杂环境之中很难被直接测量,而结构的响应相对容易获得,因此借助结构响应对载荷进行估计是解决该问题最为有效的途径之一.
结构动载荷识别是结构动力学中的第二类逆问题,其特点为已知系统特性和响应来识别动载荷,动载荷识别方法是20世纪70年代中期为研究飞机飞行过程中受载情况所提出的.求解这类问题的主要方法分为时域法和频域法[1].近年来,动载荷识别技术得到了长足的发展[2-3],基于以上两种方法,许多学者提出了一些新的方法,如神经网络法[4]、小波分析法[5].根据求解过程可将上述方法分为两大类,即迭代法和非迭代法.
迭代法的应用较为广泛.Cui等[6]使用梯度法反演了具有再生冷却系统的超燃冲压发动机燃烧室不可达表面的边界条件,其计算结果表明这种迭代算法在反演边界条件时对初值不敏感且有较强的鲁棒性,即使存在一定的测量误差,边界条件的反演结果也有着较高的精度;Wang等[7]建立了具有时间-空间解耦特性的双分散模糊推理方法来反演热流边界条件,并与动态矩阵控制法进行对比,其结果表明双分散模糊推理反演方法可以显著降低反演结果对测点个数的依赖程度,提高算法的抗干扰能力,具有较好的抗逆性;周焕林等[8]将共轭梯度法引入到布谷鸟算法中,通过变换把含热源的二维瞬态热传导问题转换为无热源的二维瞬态热传导问题,数值算例结果显示该算法在保证精度的前提下对初始值不敏感,与原始布谷鸟算法相比迭代次数大幅降低;王一博等[9]基于精细积分法推导了传热反问题对应的灵敏度矩阵,并对传热问题中的热物性参数、边界条件及热源等有关项进行了多宗量辨识.迭代法在动载荷识别领域也有着广泛的应用.Wang等[10]使用了一种新的共轭梯度法来识别三维板上的多源动态载荷,并与Landweber迭代法相比较,其数值算例表明,这种新的共轭梯度法可以提供更有效、数值稳定的反演载荷;Xu等[11]提出了一种不完全实测激励下的加权自适应迭代最小二乘估计方法,采用无噪声测量和噪声污染数据对六层数值剪切模型结构进行了数值模拟,验证了该方法的有效性;徐训等[12]提出了基于独立分量分析的多源动态载荷识别方法,解决了桁架结构在系统未知的情况下载荷波形的识别问题,并从输入、系统、输出及噪声影响4个方面分析了算法的有效性,数值仿真结果表明,算法在这4个方面都具有较好的鲁棒性.
这些方法可以通过结构响应准确地识别结构上的动态载荷,但是计算成本较高,通常耗时很长.因此,需要探寻一种非迭代反演方法,以提高计算效率,降低计算成本.
近年来非迭代反演方法研究也有较快进展.2013年,王静等[13]结合精细积分法,提出了一种新的时域动载荷识别方法,数值结果表明采用截断奇异值方法可在一定程度上克服噪音的不利影响,改善载荷的识别结果;2014年,Liu等[14]提出了一种移动最小二乘拟合形函数法,并采用正则化方法克服了载荷重构的病态性,该方法可以平稳地逼近负载,改善了系统的病态性,并通过反演车门上的动载荷验证了最小二乘拟合形函数法的有效性;2016年,彭凡等[15]将Green函数法应用于具有整体刚体平动的自由结构载荷识别问题,以测点的绝对运动加速度响应为输入,反演了整体平动自由结构的动载荷;Yu等[16-17]使用非迭代方法对传热问题的边界条件、几何形状进行了快速反演并取得了较为准确的结果,但该方法对于动载荷识别还需要进一步研究.
对于非迭代法识别结构动载荷问题,系统的病态性是导致识别结果精度不高的主要原因[18],为了消除或降低系统的病态性,许多正则化方法被研究,例如Tikhonov正则化方法[19]、奇异值分解法[20]和基函数展开法[21]等,其中基函数展开法可以有效地降低系统的病态性并且可显著提高计算效率,本文将采用基函数展开法和奇异值分解法来提高算法的抗不适定性.
通常测量信息的准确度与反演结果息息相关,本文采用经典有限元法[22]和Newmark-β法[23]求解正问题,基于有限元法建立测点响应与待演参量之间的关系,从而实现动载荷的快速识别.
1 正问题求解
本文基于线弹性动力学基本假定,建立了二维问题的动载荷识别方法理论.二维动力学问题基本控制方程如下:
运动方程
(1)
应变位移关系
(2)
应变应力关系
σij=Dijklεkl;
(3)
应力边界条件
(4)
位移边界条件
(5)
其中i, j=1,2,σij,εij,ui分别为应力、应变和位移张量,Dijkl,ρ,nj为二维动力学问题中的弹性矩阵张量、系统的密度和法向量大小,![]() 为已知的体力、面力和位移量,Sσ,Su为给定面力边界和给定位移边界.
为已知的体力、面力和位移量,Sσ,Su为给定面力边界和给定位移边界.
本文采用Galerkin有限元法进行动力分析,并使用Newmark-β法进行时域分析,在t+Δt时刻有
(6)
其中Δt为时间步长,将![]() 与
与![]() 采用以下形式来表示:
采用以下形式来表示:
(7)
(8)
式中![]() 将式(7)和(8)代入到式(6)中,整理得到
将式(7)和(8)代入到式(6)中,整理得到
(9)
其中
(10)
(11)
本文采用的是Newmark-β法中的平均加速度假设,即![]()
2 载荷识别过程
2.1 推导位移响应与待演参量之间的关系
在载荷识别过程中,施加在系统上的载荷Ft是未知的,需要获得系统上一些节点的位移,再寻找这些节点的位移与待演参量之间的关系来求解载荷的大小,这些节点被称为测点.本文中测点的位移采用正问题计算获得.
为获得测点位移与待演参量之间的关系,需将各矩阵进行分块处理,假设全域中总节点的个数为Na,施加力边界条件的节点个数为Nf,测量节点的个数为Nm,施加位移边界条件的节点个数为Nd.但一般位移边界条件为固支,其值为0,因此在进行矩阵划分时可以省略这些数据,域内其他节点个数为No=Na-Nf-Nm-Nd,则式(6)中矩阵被划分为
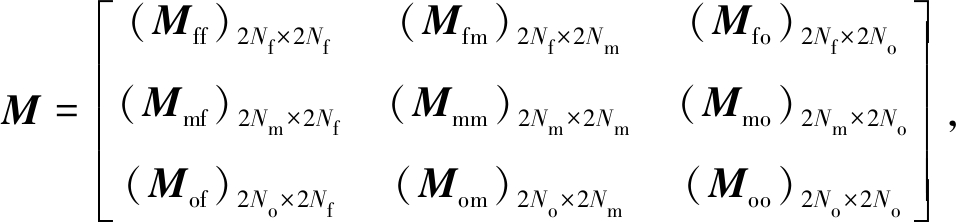
(12)
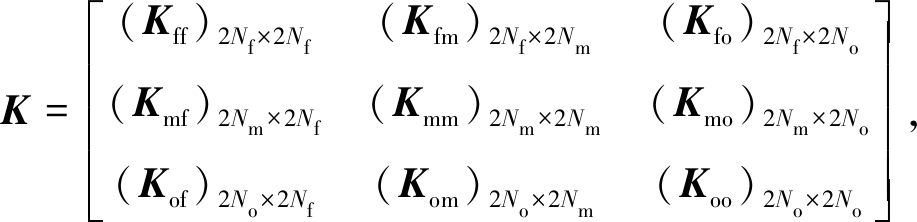
(13)

(14)
(15)
(16)
(17)
(18)
将式(12)~(18)代入式(10)、(11),再将得到的![]() 进行相应的划分,可得
进行相应的划分,可得
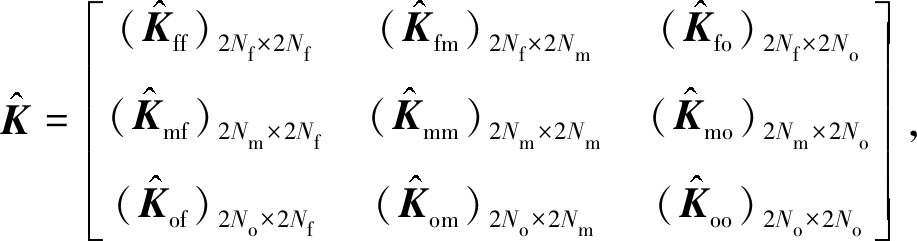
(19)
(20)
将式(19)和(20)代入式(9),可得
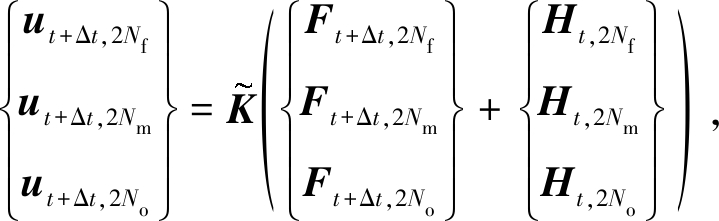
(21)
其中![]() 对
对![]() 进行矩阵划分有
进行矩阵划分有
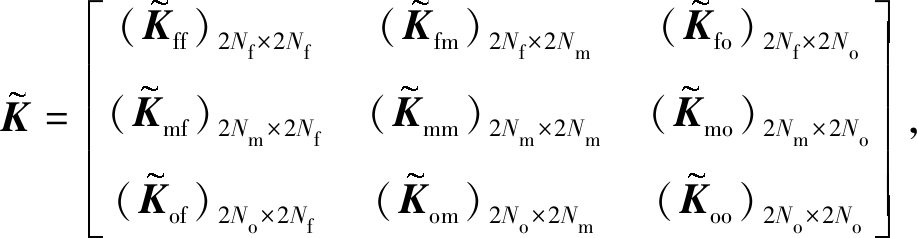
(22)
耦合式(21)、(22)可得
(23)
其中
则式(23)即为测点位移和待演参量之间的关系.
2.2 建立误差函数
与迭代反演方法类似,引入误差函数:
J=(ut+Δt,2Nm-(ut+Δt,2Nm)r)T(ut+Δt,2Nm-(ut+Δt,2Nm)r),
(24)
其中(ut+Δt,2Nm)r为t+Δt时刻的测量信息.
基于最小二乘法原理,令∂J/∂Ft+Δt,2Nf=0,可得
(25)
通过求解式(25)即可求得待演参量Ft+Δt,2Nf.
本文将集中载荷和分布载荷均等效为节点上的集中载荷进行分析.在式(25)中ATA是病态的,这将直接影响计算结果的准确与稳定性,本文采用奇异值分解法进行求解.同时,对于反演分布载荷问题,为了提高反演精度,提高算法的抗不适定性和降低计算的维度,本文采用二次基函数对待演参量进行展开,将原问题转化为求解待定系数问题.以二维动力问题为例,由于待演参量具有两个自由度,因此展开基函数为
(26)
式中
(27)
xi,yi表示识别载荷节点i的横坐标和纵坐标,Nf为施加力边界条件的节点个数,则在每个时间段有
Ft+Δt,2Nf=Φαt+Δt,
(28)
式中
(29)
将式(28)代入式(23)得到
ut+Δt,2Nm=Dαt+Δt+A,
(30)
其中![]() 再根据式(24)、(25)可得到
再根据式(24)、(25)可得到
αt+Δt=(DTD)-1DT((ut+Δt,2Nm)r-A).
(31)
根据上式求得的αt+Δt,代入式(28)便可以求得每一时间段的Ft+Δt,2Nf,基本流程图如图1所示.
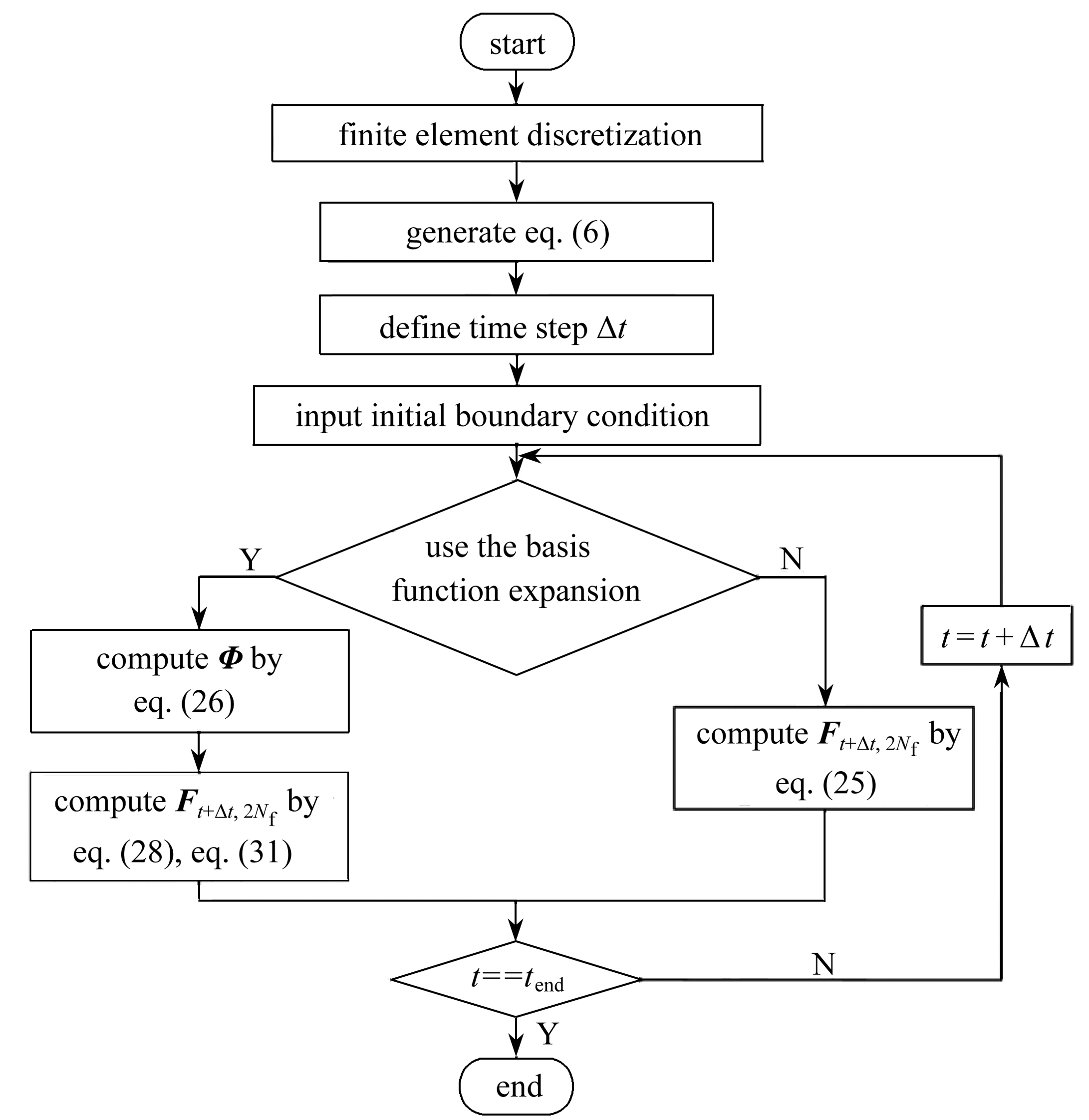
图1 载荷识别流程图
Fig. 1 The load identification flow chart
3 数 值 算 例
为模拟真实测量环境,本文对正问题计算获得的位移施加一定的噪声来代替测点位移,具体表达式如下:
(ut,2Nm)r=ut,2Nm+ε·σ(ut,2Nm)·R,
(32)
其中(ut,2Nm)r为真实的测点位移,ut,2Nm为正问题计算所得测点的位移响应,σ(ut,2Nm)是计算所得测点位移的标准差,ε是百分数代表的噪声水平,R是均值为0、方差为1的一组随机数.
为验证方法的准确性和衡量其他因素的影响程度,采用绝对误差Vabserr和某些时刻的均方根误差Vrmserr来衡量:
Vabserr=|Finverse,i(t)-Fexact,i(t)|,
(33)
(34)
式中i表示识别载荷的节点,F表示节点上所施加的载荷量,其下标“inverse”和“exact”分别表示反演的载荷和真实施加的载荷.
3.1 算例1
1) 噪声水平的影响
该算例考虑一端固支方板结构,结构形式如图2所示,长4 m,宽3 m,弹性模量E=7×1010 Pa,Poisson比υ=0.33,密度ρ=2 700 kg/m3.方板上端固支,下端施加两个冲击载荷f1(t), f2(t):
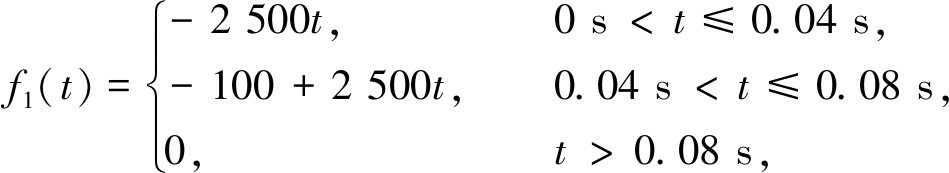
(35)

(36)
载荷的单位为N.该问题可按照平面应力问题求解且不考虑阻尼的影响,将整个域划分为300个四边形单元,计算时间区间为0.15 s,时间步长为0.01 s,初始时刻静止.选取的噪声水平为ε=1%,3%,5%,单元划分和测点选取的情况如图3所示.
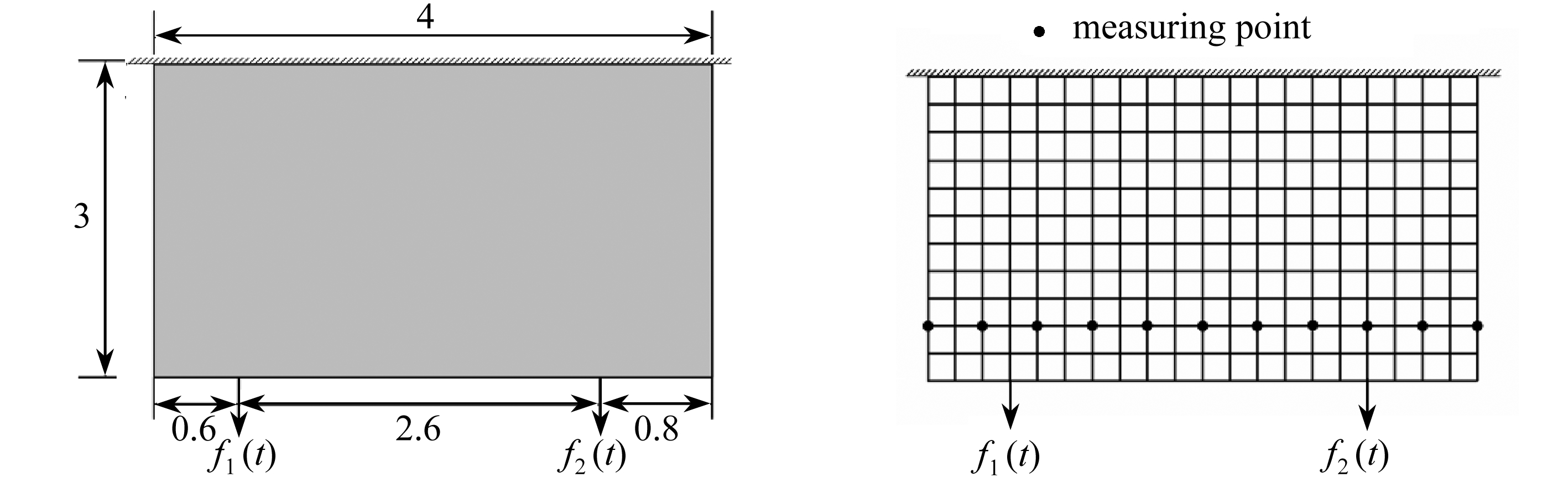
图2 方板受力状态(单位: m)图3 单元划分和测点选择
Fig. 2 Loads on the square plate(unit: m)Fig. 3 Elements and measuring points
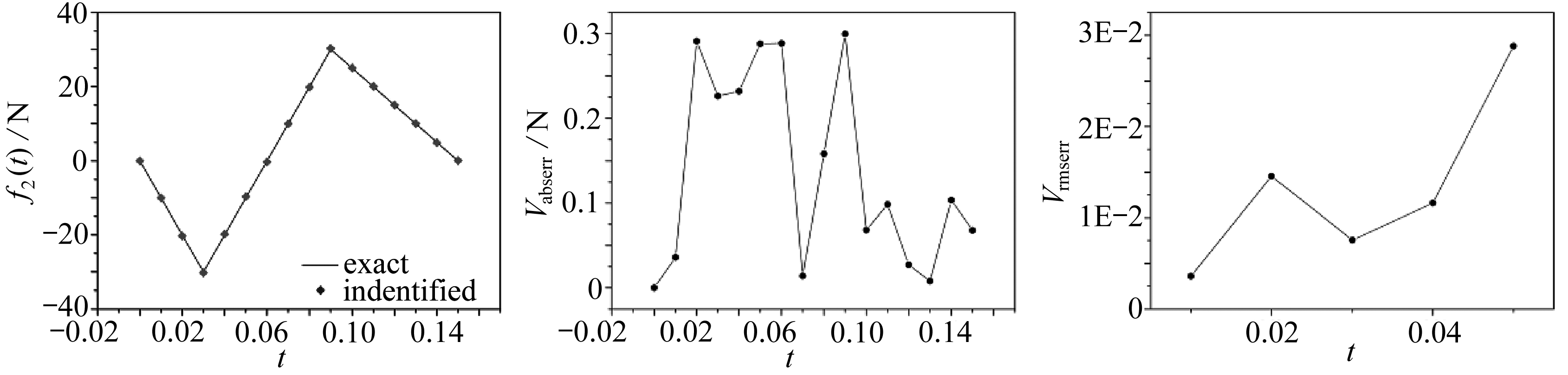
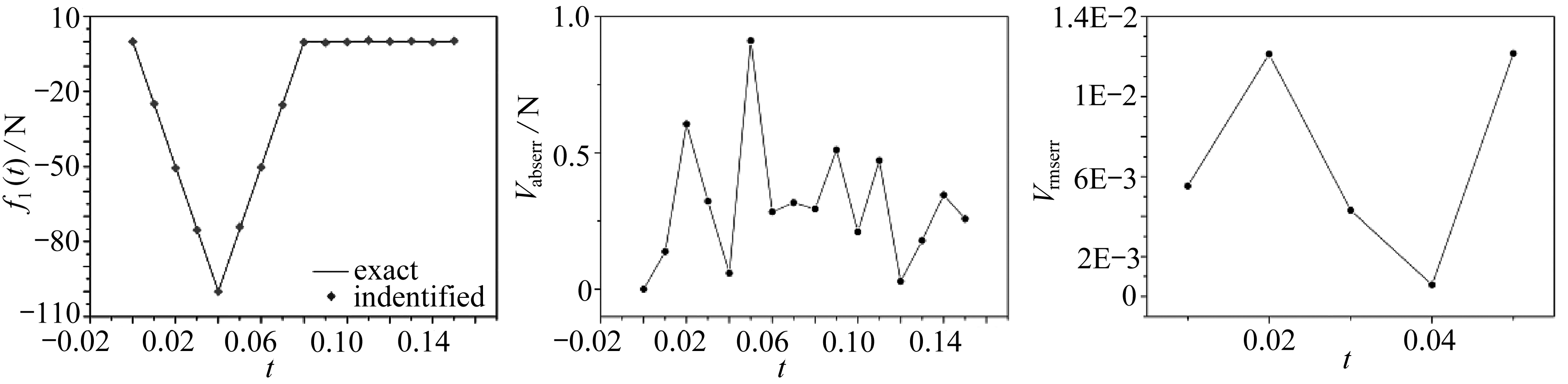
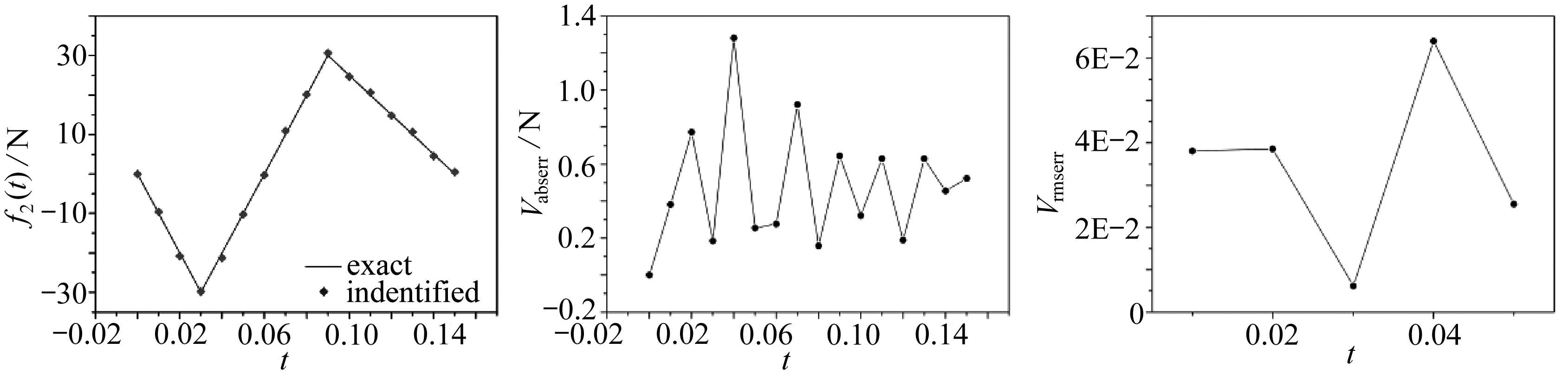
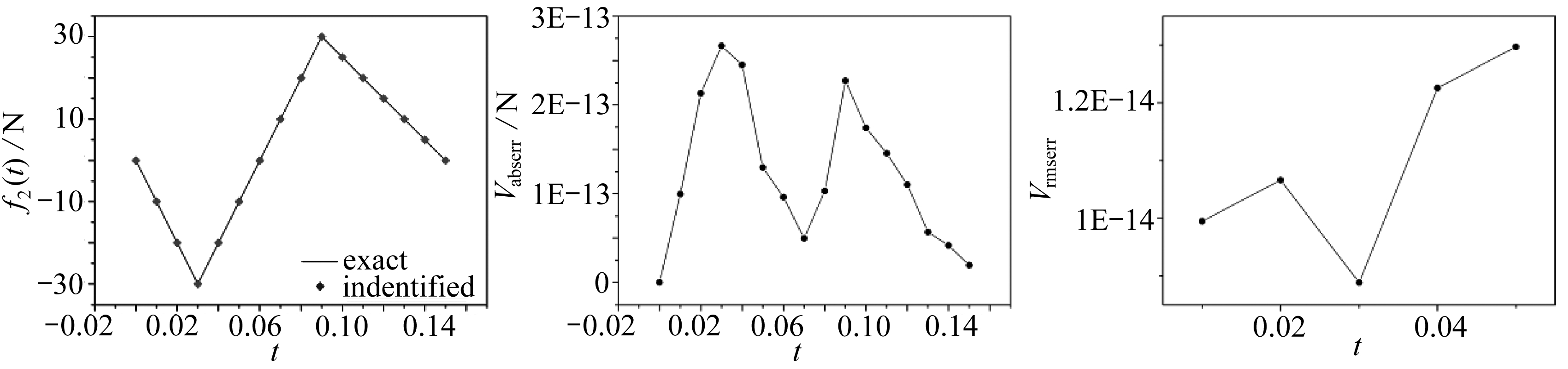
由图4可知,该方法在不同噪声水平下识别动态载荷时,整体上和实际值是相符的,在ε=0%时,对f1(t), f2(t)反演的结果均十分准确,Vabserr处于10-13~10-12量级,Vrmserr处于10-14量级,说明目前方法可以获得精度较高的反演结果.随着噪声水平的增加,Vabserr也随之增加, f1(t), f2(t)反演最大Vabserr出现在ε=5%时,最大Vabserr分别为0.93,1.28 N.Vrmserr在ε=0%时最小,在其他噪声水平处Vrmserr基本稳定,大部分在10-3~10-2量级,该算例说明该方法具有较好的抗噪性,即使在噪声水平为ε=5%的情况下,也能得到较为理想的结果.
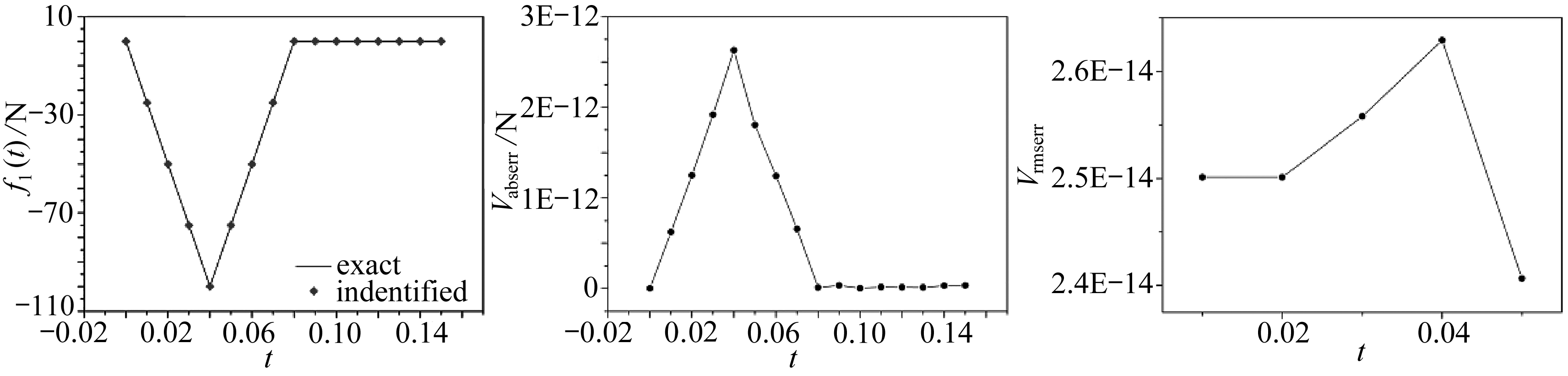
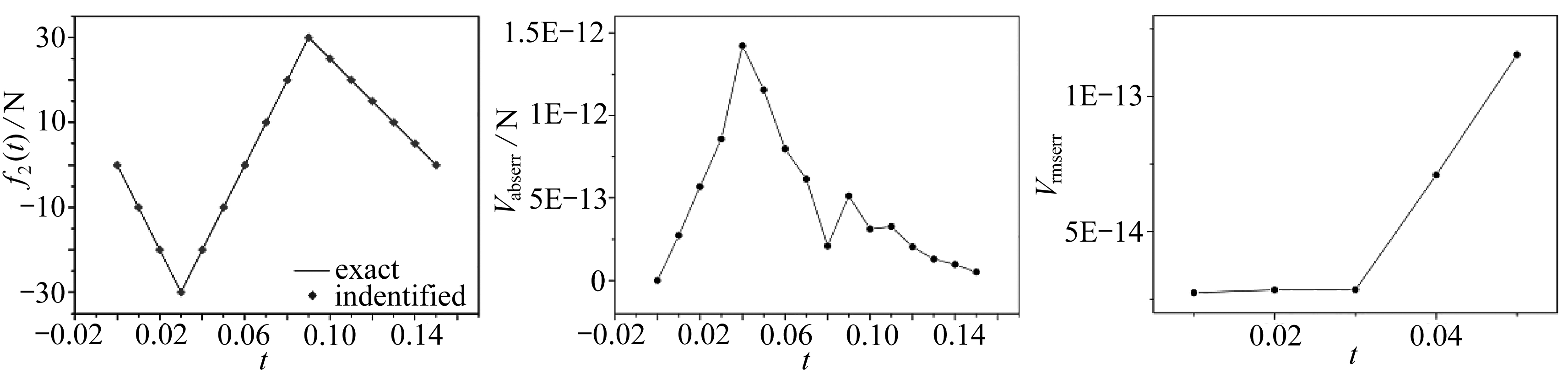
(a) ε=0%
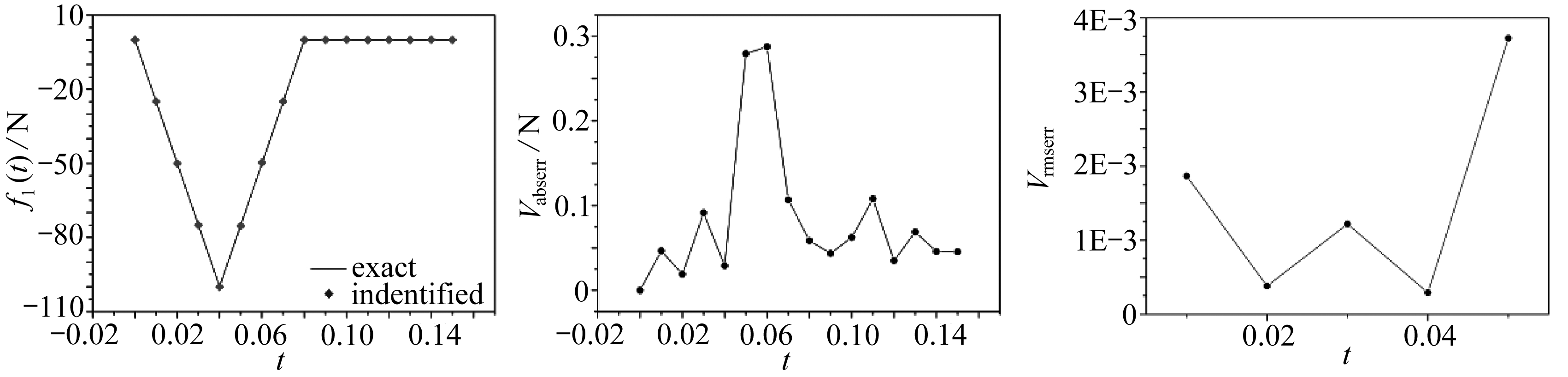
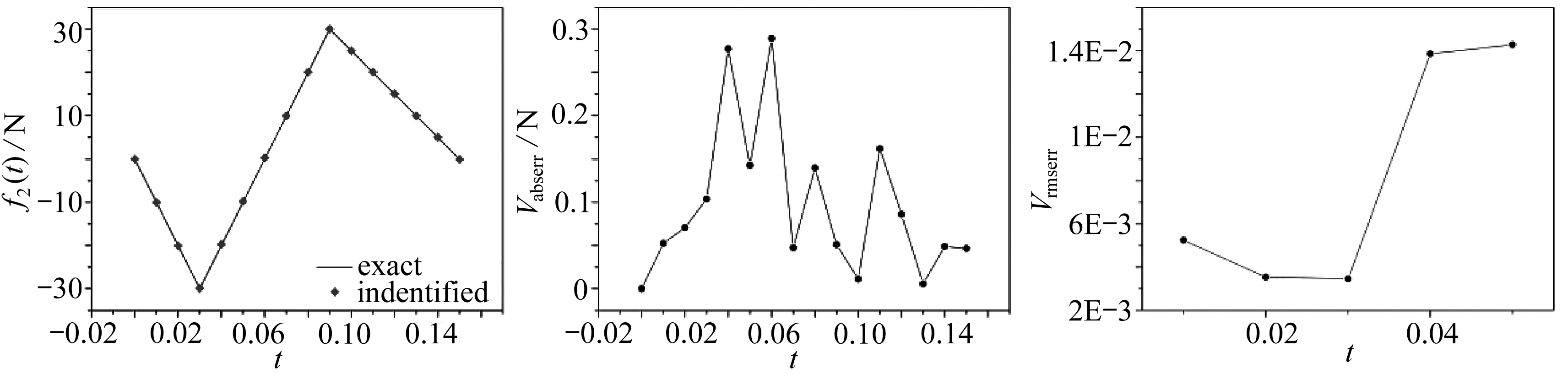
(b) ε=1%

(c) ε=3%
(d) ε=5%
图4 不同噪声水平的影响
Fig. 4 The influences of different noise levels

(a) Nm=21(b) Nm=16

(c) Nm=11(d) Nm=6
图5 不同的测点数量
Fig. 5 The different numbers of measuring points
2) 测点数量的影响
使用相同的结构形式、物性参数和受力状态以及如图3所示的单元划分情况,该结构所受的载荷大小如式(35)、(36)所示,没有噪声,计算时间区间为0.15 s,时间步长为0.01 s,初始时刻静止.选择4组不同测点来讨论测点对该方法的影响,不同数量的测点选取如图 5所示.
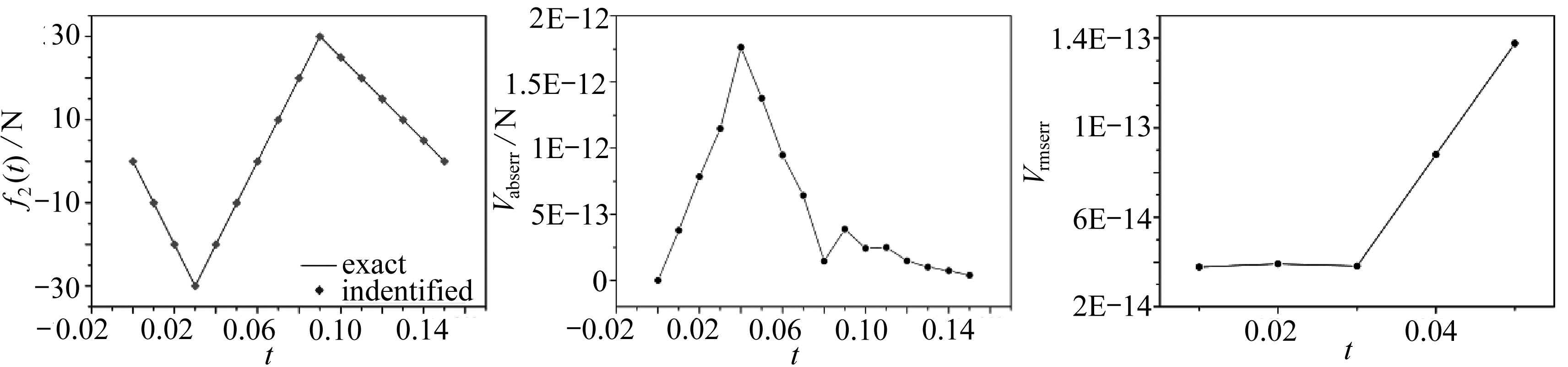
(a) Nm=21

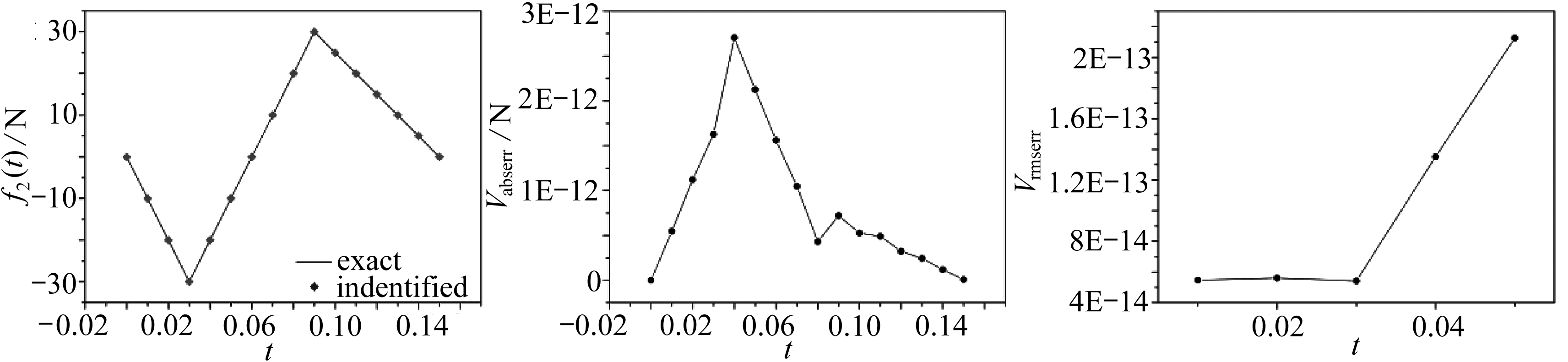
(b) Nm=16

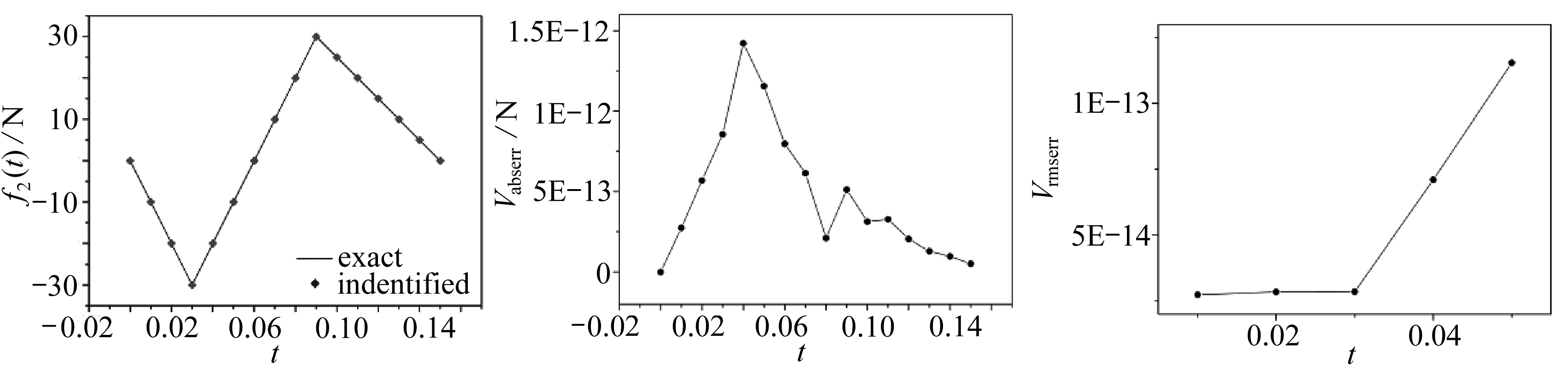
(c) Nm=11
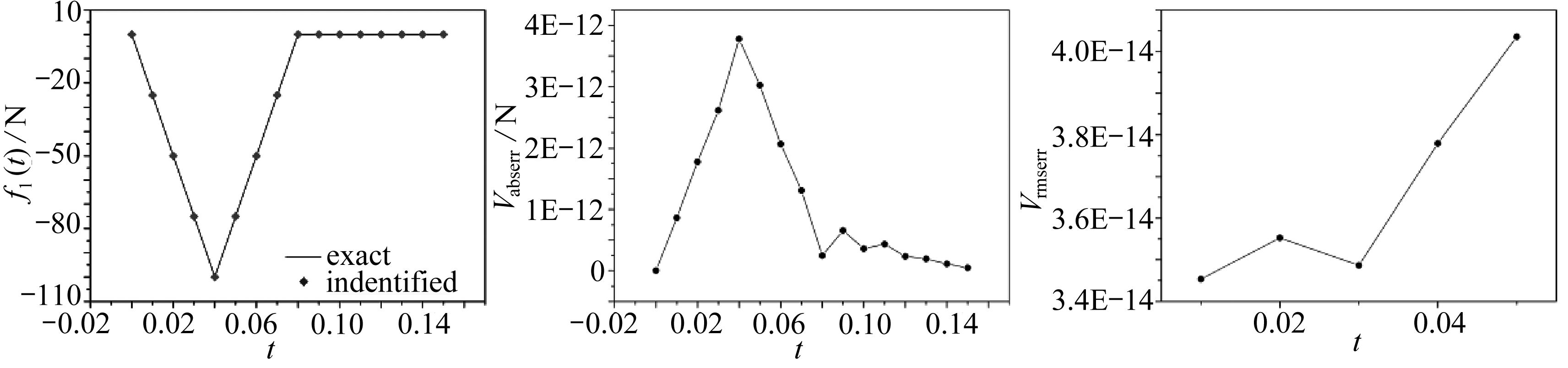
(d) Nm=6
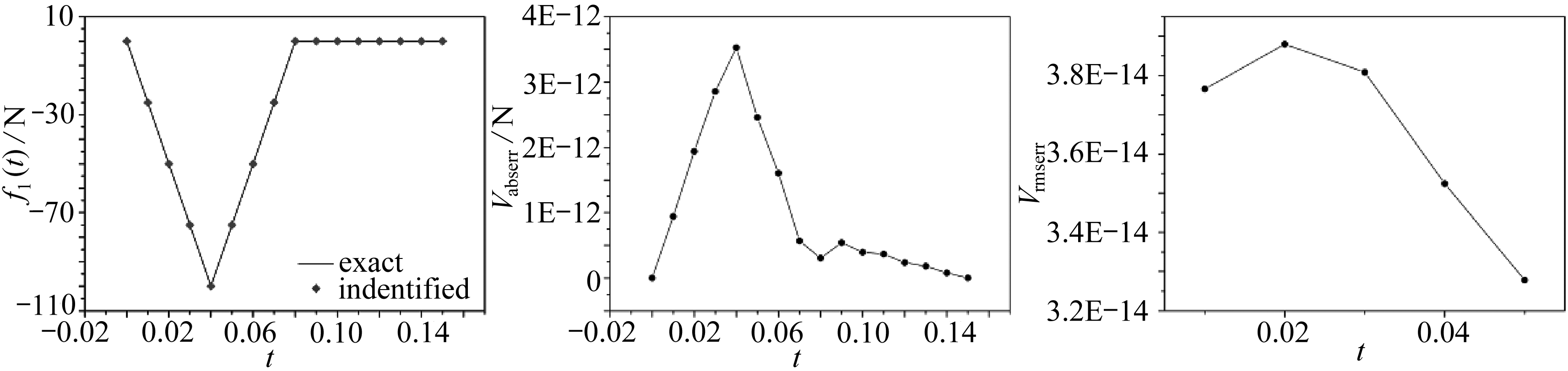
图6 不同测点数量的影响
Fig. 6 The influences of different numbers of measuring points
由图6可知在不同测点数量的情况下,Vabserr大部分处于10-13~10-12量级,Vrmserr大部分处于10-15~10-14量级,反演结果相当精确,说明该方法在反演过程中受测点数量的影响较小,即使采用6个测点也能获得较为准确的反演结果.
3.2 算例2
1) 基函数展开的影响
该算例考虑一刚性夹杂圆环.刚性夹杂圆环内边界固支,外边界施加p(t)的均布载荷,外边界Γ1半径为1 m,内边界Γ2半径为0.5 m,弹性模量E=7×1010 Pa,Poisson比υ=0.33,密度ρ=2 700 kg/m3.结构图如图7所示,施加的均布载荷p(t)为
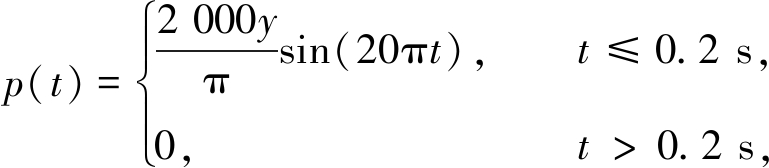
(37)
载荷的单位为N/m,该问题可按平面应力问题求解且不考虑阻尼的影响,并按照有限元方法将均布载荷转化为节点载荷来求解.将整个域划分为200个四节点四边形单元,计算时间区间为0.3 s,时间步长为0.01 s,初始时刻静止,没有测量噪声,其单元划分和测点选择如图8所示.本算例主要讨论基函数展开对该算法的影响.
由图9和图10可知,直接反演的结果在趋势上和实际值基本一致,但图像中有较为明显的毛刺,其绝对误差最大接近6 N.而使用二次基函数展开所得的反演结果则十分平滑,绝对误差的量级也有了显著的提升,大都在10-5量级,说明基函数展开对该算法精度有显著的提升.因此在处理均布载荷时,使用基函数展开可以得到更好的结果.

图7 圆环受力状态图8 单元划分和测点的选择
Fig. 7 Loads on the ringFig. 8 Elements and measuring points
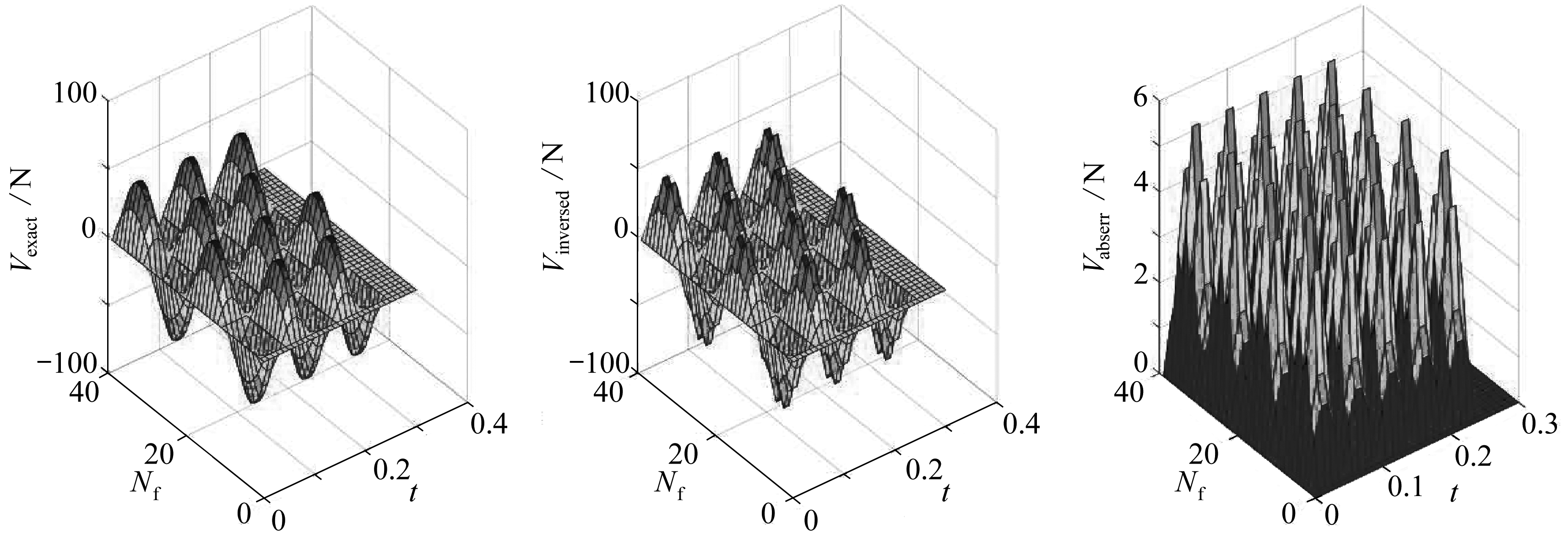
图9 直接反演结果
Fig. 9 Directly inversed results
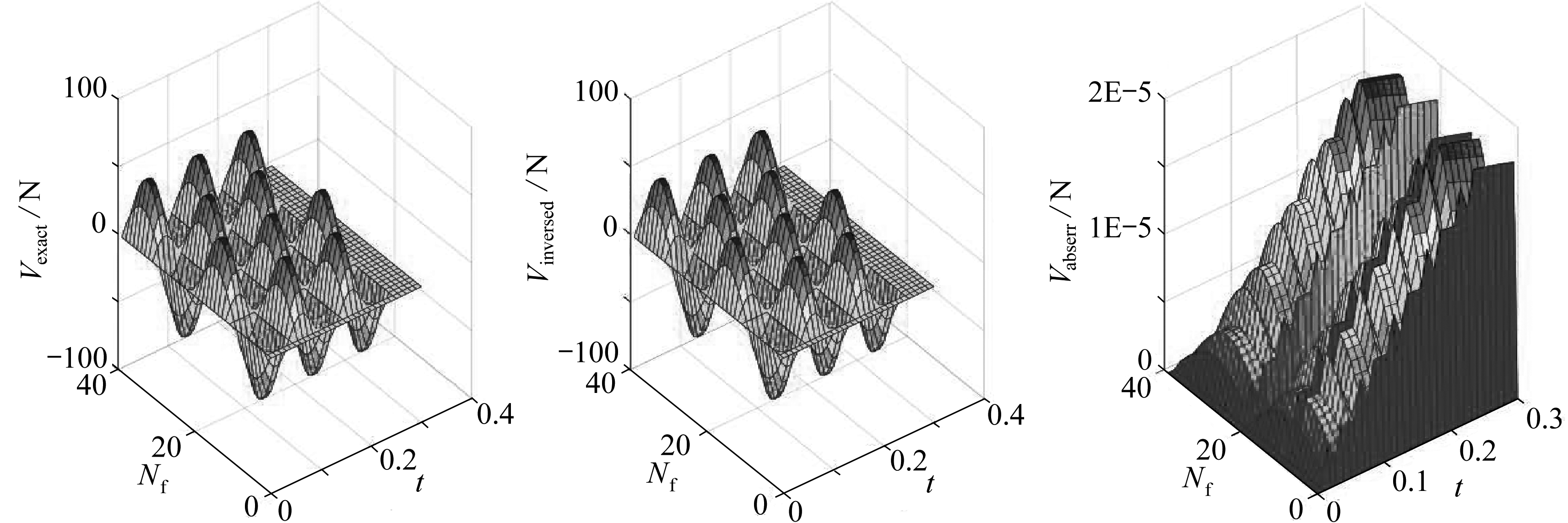
图10 采用二次基函数展开的反演结果
Fig. 10 The inversed results with the quadratic basis function expansion
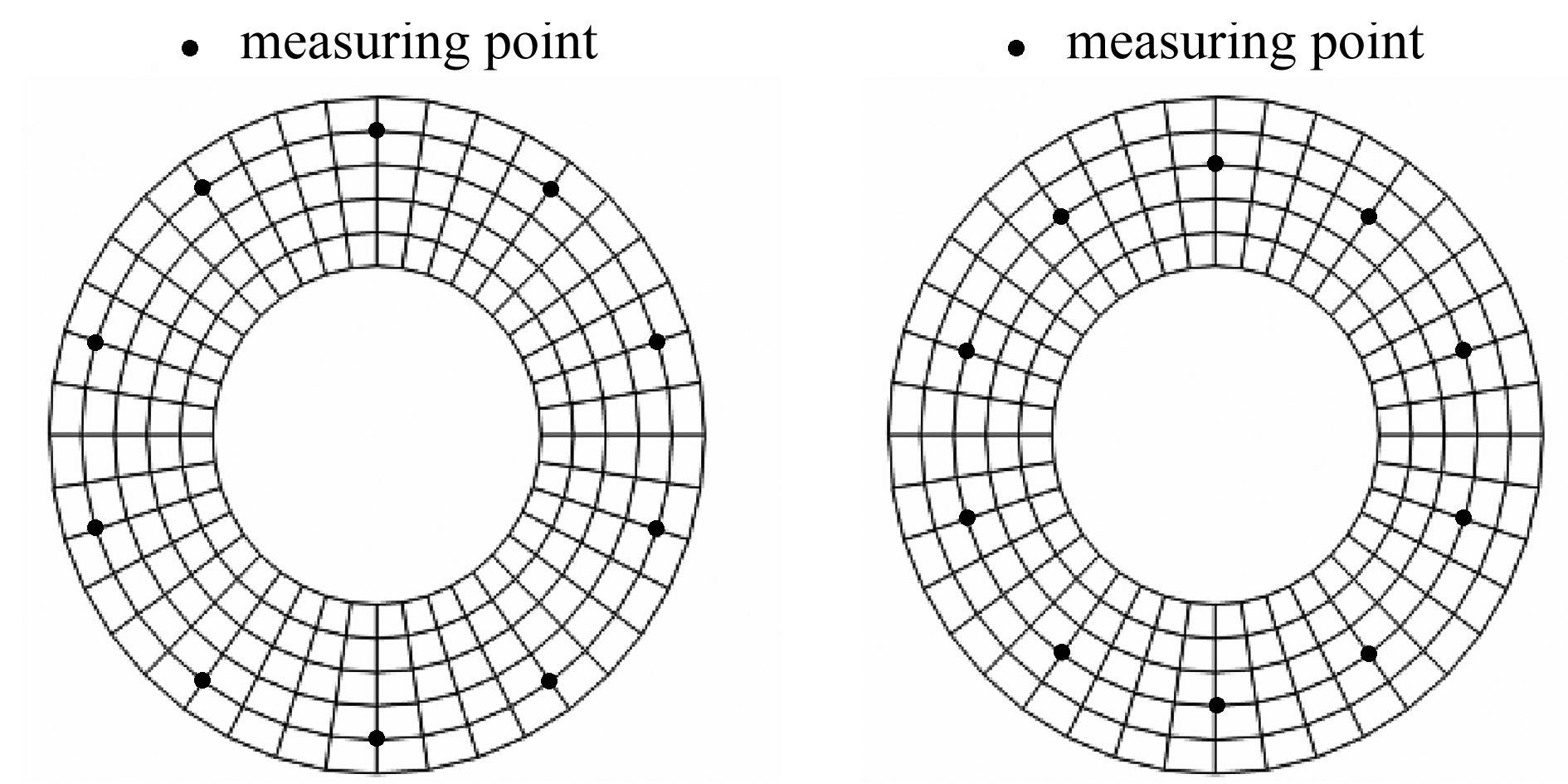
(a) R=0.9 m(b) R=0.8 m
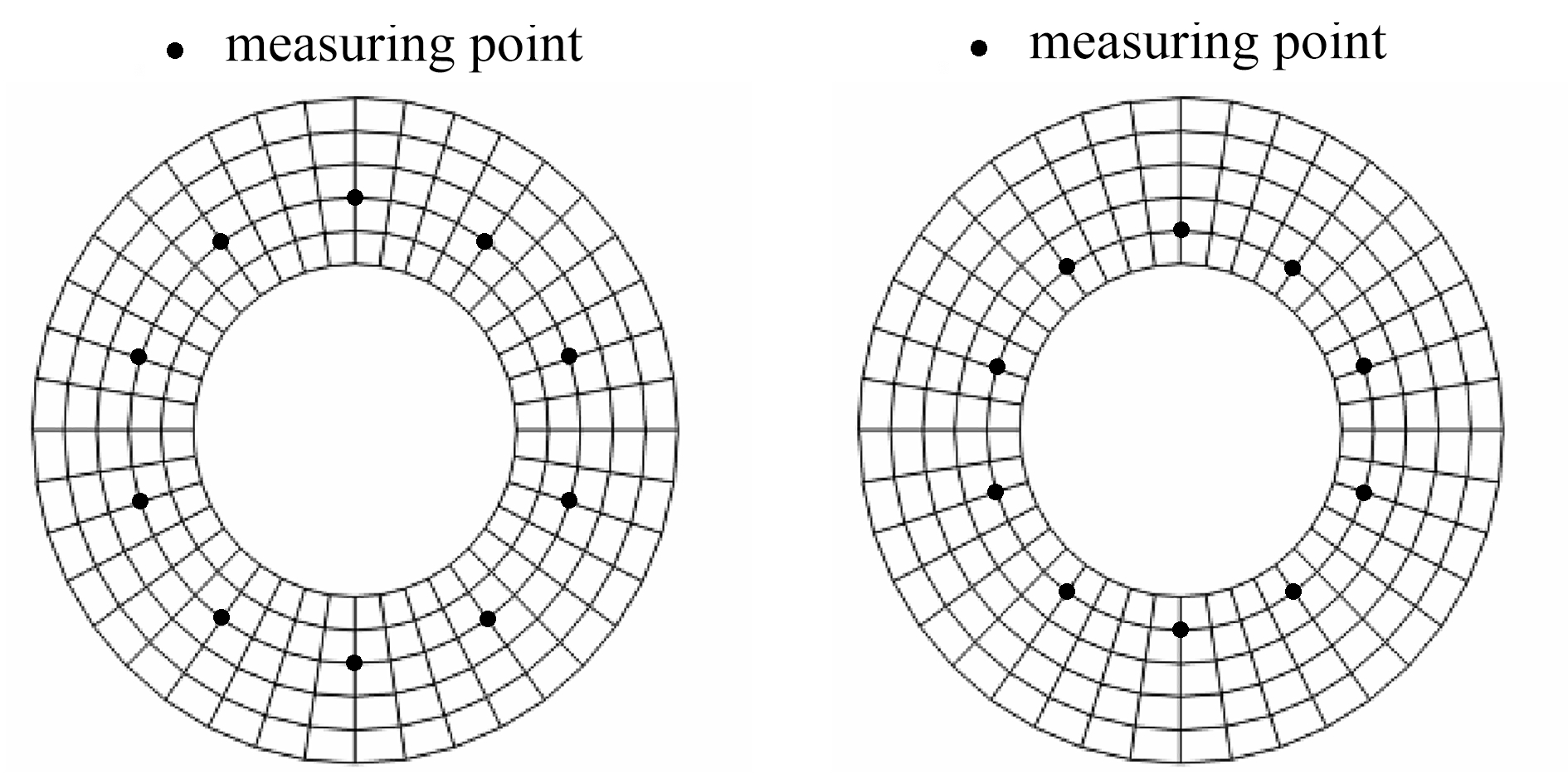
(c) R=0.7 m(d) R=0.6 m
图11 不同的测点位置
Fig. 11 The different locations of measuring points
2) 测点位置的影响
使用图7给定的结构形式、物性参数和受力状态,其所受的均布载荷的大小如式(37)所示,分别在不同位置选择10个测点(如图11所示),来研究测点位置对该算法的影响,计算时间区间为0.3 s,时间步长为0.01 s,初始时刻静止,没有测量误差.
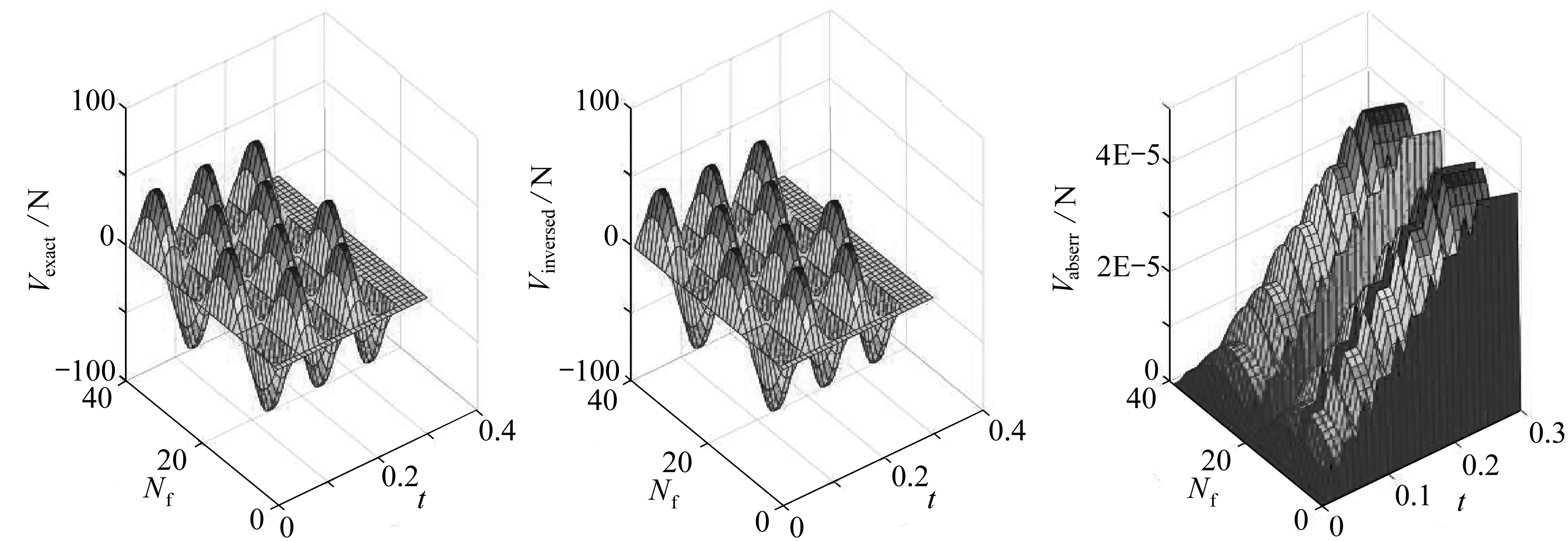
(a) R=0.9 m
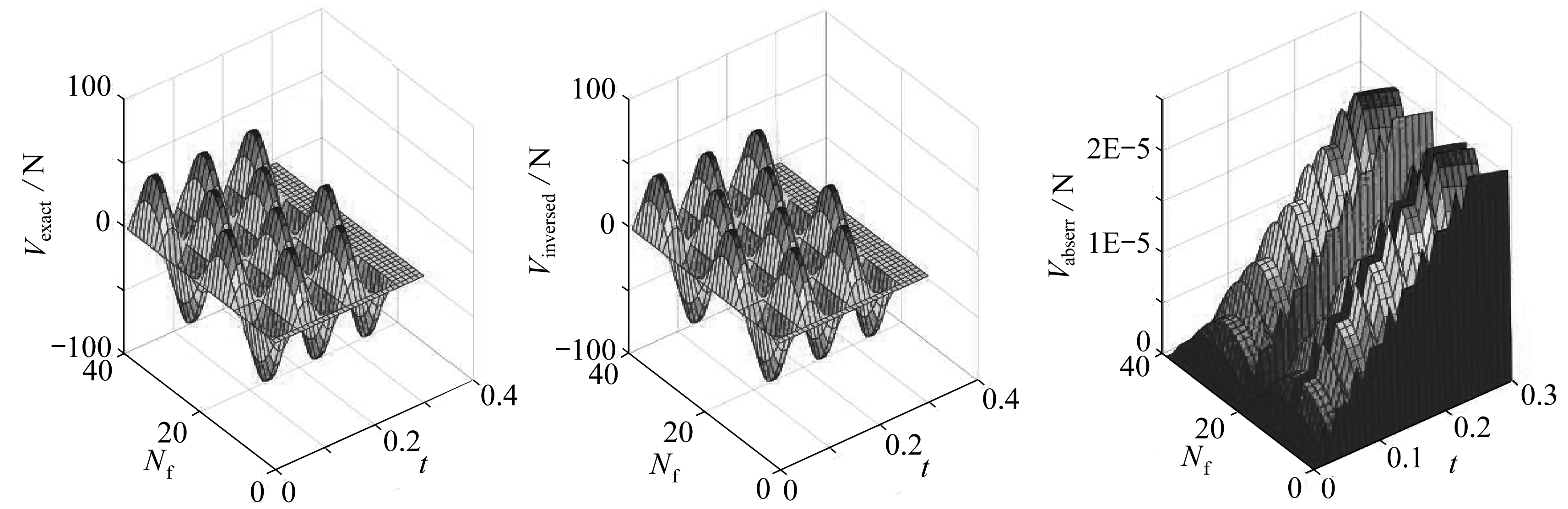
(b) R=0.8 m
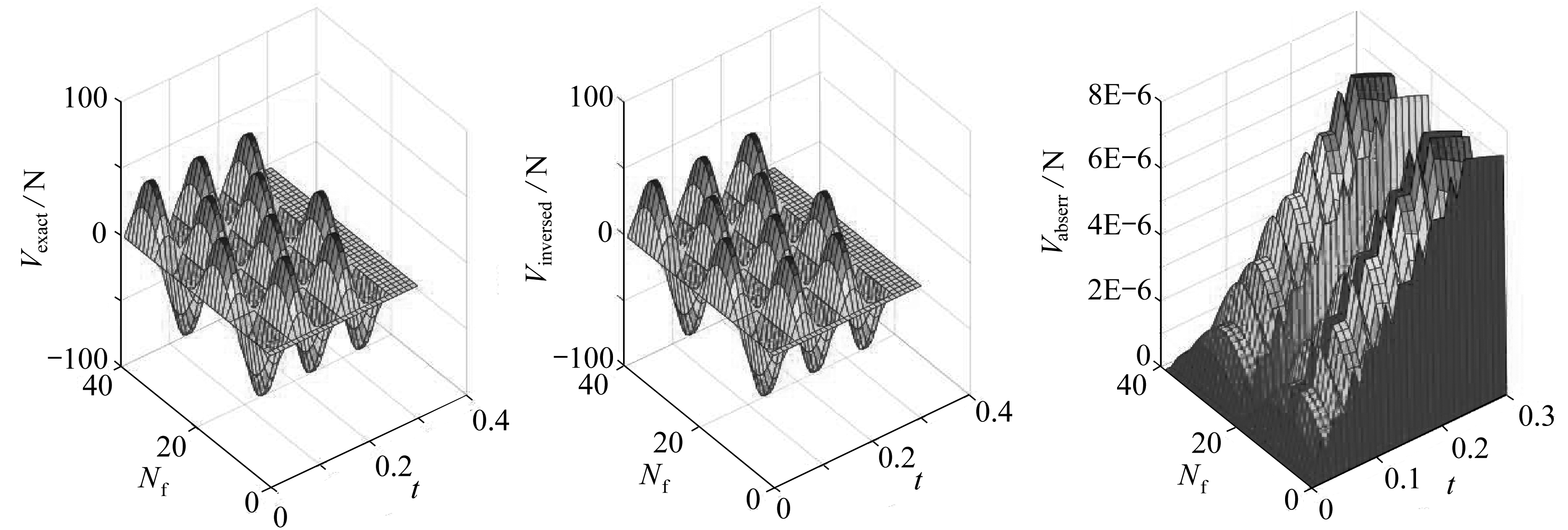
(c) R=0.7 m
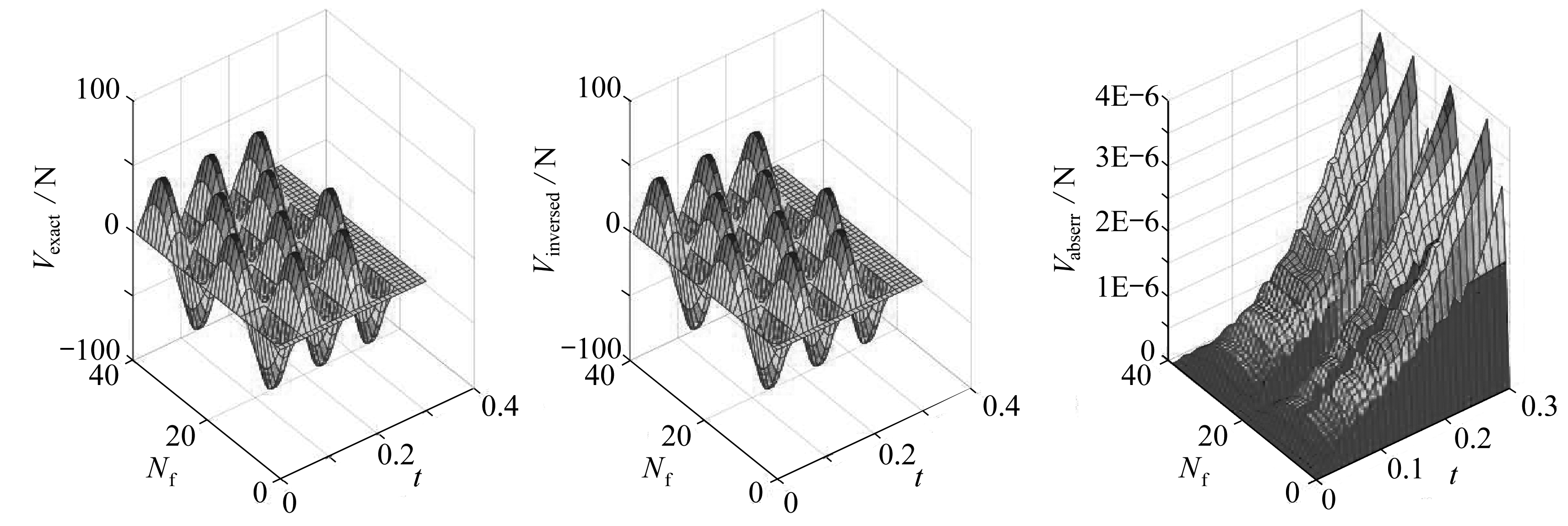
(d) R=0.6 m
图12 不同测点位置的影响
Fig. 12 The influences of different locations of measuring points
由图12可知,采用不同位置的测点,反演结果与实际施加的载荷高度吻合,曲线都很平滑,绝对误差上下波动不大且均处于10-5~10-6量级.说明测量点的位置对该算法的影响不大.
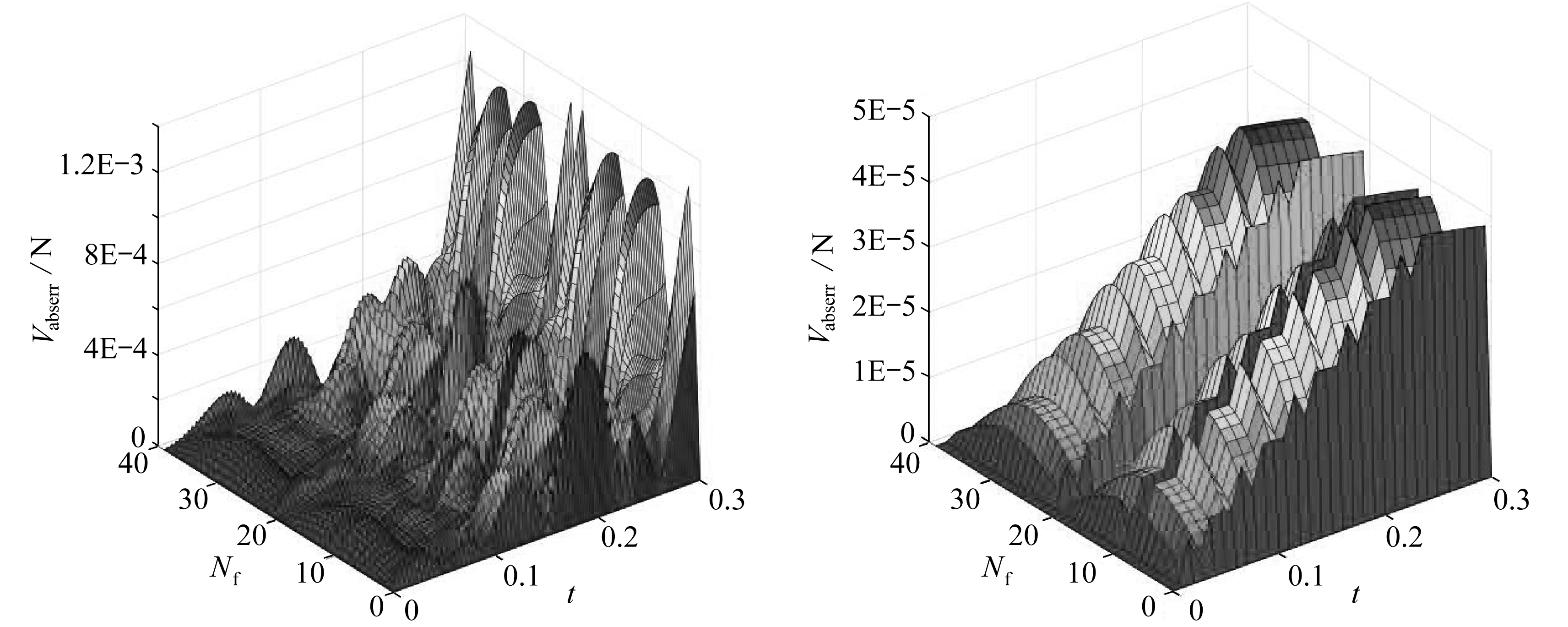
图13 时间步长为0.001 s时反演结果的绝对误差图14 时间步长为0.01 s时反演结果的绝对误差
Fig. 13 Vabserr of inversed results with a time step of 0.001 sFig. 14 Vabserr of inversed results with a time step of 0.01 s
3) 时间步长的影响
本文通过逐步推进实施反演,一般反演过程中每一步均存在不同程度的误差,该部分通过采取不同的时间步长来讨论反演过程中误差的累积情况.采用如图7所示的结构形式、物性参数和受力状态,利用图8所示的网格划分和测点的选择以及式(37)所示的载荷大小,计算时间区间为0.3 s,时间步长分别为0.001 s和0.01 s,初始时刻静止.
由图13、14可知,随着时间步长的减小,即计算次数的增多,该算法会产生一定的误差积累,由于时间步长的减小反演结果的Vabserr由10-5量级增加到了10-3量级,但反演结果还是令人满意的.
3.3 算例3
本文提出的算法同样可以应用到平面梁单元中,推导梁单元的载荷识别公式与平面单元类似.取一个平面悬臂梁,弹性模量E=9.8×107 Pa,Poisson比υ=0.33,密度ρ=1 000 kg/m3,梁长4 m,其横截面为0.3 m×0.4 m的矩形.其结构形式如图15所示,梁自由端承受的载荷为
(38)
载荷的单位为N,将该梁划分成10个梁单元,计算时间区间为0.12 s,时间步长为0.01 s,初始时刻静止.

图15 悬臂梁受力状态
Fig. 15 Loads on the cantilever beam

图16 悬臂梁的反演结果
Fig. 16 The inversed results of the cantilever beam
由图16可以看出反演的结果与实际的载荷高度吻合,Vabserr处于10-10~10-9量级之间,反演结果说明该算法可以准确反演施加在梁上的动态载荷.
4 结 论
本文基于有限元法和最小二乘法通过对系统矩阵进行分块变换,提出了一种新的非迭代反演方法对结构上的动载荷进行识别.该方法的计算成本主要在于形成有限元法计算模型的相应矩阵和求解对误差函数求极值而形成的病态方程组,因此该方法可实现快速反演.在反演过程中利用奇异值分解法和二次基函数展开技术,提高了方法的抗不适定性,同时获得了高精度的反演结果.通过考虑噪声水平、测点数量、基函数展开、测点位置和时间步长对反演结果的影响,针对集中载荷和分布载荷情况实现了快速准确地识别.同时验证了该算法适用于其他结构,例如悬臂梁.算例结果表明,该方法在识别动载荷时具有较高的准确性和数值稳定性.
[1] 韩旭, 刘杰, 李伟杰, 等. 时域内多源动态载荷的一种计算反求技术[J]. 力学学报, 2009, 41(4): 595-602.(HAN Xu, LIU Jie, LI Weijie, et al. A computational inverse technique for reconstruction of multisource loads in time domain[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 595-602.(in Chinese))
[2] 毛玉明, 林剑锋, 刘靖华, 等. 动载荷反演分析技术研究综述[J]. 动力学与控制学报, 2014, 12(2): 97-104.(MAO Mingyu, LIN Jianfeng, LIU Jinghua, et al. Recent advances of dynamic force estimation techniques[J]. Journal of Dynamics and Control, 2014, 12(2): 97-104.(in Chinese))
[3] 杨志春, 贾友. 动载荷的识别方法[J]. 力学进展, 2015, 45: 29-52.(YANG Zhichun, JIA You. The identification of dynamic loads[J]. Advances in Mechanics, 2015, 45: 29-52.(in Chinese))
[4] 郑敏, 任芳, 杨兆建, 等. 自适应BP神经网络的转子系统载荷识别的研究[J]. 机械设计与制造, 2016, 6: 85-88, 92.(ZHENG Min, REN Fang, YANG Zhaojian, et al. Study on the load identification of the rotor system with self-adaptive BP neural networks[J]. Machinery Design & Manufacture, 2016, 6: 85-88, 92.(in Chinese))
[5] 杨帆, 张方, 姜金辉. 正交小波级数拟合法的薄板结构分布动载荷识别技术[J]. 北京理工大学学报, 2014, 34(6): 561-564.(YANG Fan, ZHANG Fang, JIANG Jinhui. Orthogonal wavelet series fitting in identification of distributed load for thin plate model[J]. Transactions of Beijing Institute of Technology, 2014, 34(6): 561-564.(in Chinese))
[6] CUI M, MEI J, ZHANG B W, et al. Inverse identification of boundary conditions in a scramjet combustor with a regenerative cooling system[J]. Applied Thermal Engineering, 2018, 134: 555-563.
[7] WANG G J, WAN S B, CHEN H, et al. A double decentralized fuzzy inference method for estimating the time and space-dependent thermal boundary condition[J]. International Journal of Heat & Mass Transfer, 2017, 109: 302-311.
[8] 周焕林, 严俊, 余波, 等. 识别含热源瞬态热传导问题的热扩散系数[J]. 应用数学和力学, 2018, 39(2): 160-169.(ZHOU Huanlin, YAN Jun, YU Bo, et al. Identification of thermal diffusion coefficients for transient heat conduction problems with heat sources[J]. Applied Mathematics and Mechanics, 2018, 39(2): 160-169.(in Chinese))
[9] 王一博, 杨海天, 邬瑞锋. 基于时域精细积分算法的瞬态传热多宗量反演[J]. 应用数学和力学, 2005, 26(5): 512-518.(WANG Yibo, YANG Haitian, WU Ruifeng. Precise integral algorithm based solution for transient inverse heat conduction problems with multi-variables[J]. Applied Mathematics and Mechanics, 2005, 26(5): 512-518.(in Chinese))
[10] WANG G J, WAN S B, CHEN H, et al. A double decentralized fuzzy inference method for estimating the time and space-dependent thermal boundary condition[J]. International Journal of Heat & Mass Transfer, 2017, 109: 302-311.
[11] XU B, HE J, ROGER R, et al. Structural parameters and dynamic loading identification from incomplete measurements: approach and validation[J]. Mechanical Systems and Signal Processing, 2012, 28: 244-257.
[12] 徐训, 欧进萍. 基于独立分量分析的多源动态载荷识别方法[J]. 力学学报, 2012, 44(1): 158-166.(XU Xun, OU Jinping. An identification method of multi-soure dynamic loads based on independent component analysis[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 158-166.(in Chinese))
[13] 王静, 陈海波, 王靖. 基于精细积分的冲击载荷时域识别方法研究[J]. 振动与冲击, 2013, 32(20): 81-85.(WANG Jing, CHEN Haibo, WANG Jing. A study of impulsive load identification in time domain based on precise time-integration method[J]. Journal of Vibration and Shock, 2013, 32(20): 81-85.(in Chinese))
[14] LIU J, SUN X S, HAN X, et al. A novel computational inverse technique for load identification using the shape function method of moving least square fitting[J]. Computers and Structures, 2014, 144: 127-137.
[15] 彭凡, 马庆镇, 肖健, 等. 自由运行结构动态载荷识别的格林函数法[J]. 动力学与控制学报, 2016, 14(1): 75-79.(PENG Fan, MA Qingzhen, XIAO Jian, et al. Green kernel function approach of load identification for free structures with overall translation[J]. Journal of Dynamics and Control, 2016, 14(1): 75-79.(in Chinese))
[16] YU B, YAO W A, GAO Q, et al. A novel non-iterative inverse method for estimating boundary condition of the furnace inner wall[J]. International Communications in Heat & Mass Transfer, 2017, 87: 91-97.
[17] YU B, XU C, YAO W A, et al. Estimation of boundary condition on the furnace inner wall based on precise integration BEM without iteration[J]. International Journal of Heat & Mass Transfer, 2018, 122: 823-845.
[18] SUN X, LIU J, HAN X, et al. A new improved regularization method for dynamic load identification[J]. Inverse Problems in Science & Engineering, 2014, 22(7): 1062-1076.
[19] ZHOU H L, LI Y S, YU B, et al. Shape identification for inverse geometry heat conduction problems by FEM without iteration[J]. Numerical Heat Transfer Applications, 2017, 72(8): 1-14.
[20] 迟彬, 叶庆凯. 用奇异值分解方法计算具有重特征值矩阵的特征矢量[J]. 应用数学和力学, 2004, 25(3): 233-238.(CHI Bin, YE Qingkai. Computing the eigenvectors of a matrix with multiplex eigenvalues by SVD method[J]. Applied Mathematics and Mechanics, 2004, 25(3): 233-238.(in Chinese))
[21] 张雄, 刘岩. 无网格法[M]. 北京: 清华大学出版社, 2004.(ZHANG Xiong, LIU Yan. Meshless Method[M]. Beijing: Tsinghua University Press, 2004.(in Chinese))
[22] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2015.(WANG Xucheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2015.(in Chinese))
[23] 张雄, 王天舒, 刘岩. 计算动力学[M]. 北京: 清华大学出版社, 2015.(ZHANG Xiong, WANG Tianshu, LIU Yan. Computational Dynamics[M]. Beijing: Tsinghua University Press, 2015.(in Chinese))