引 言
仓室模型是描述传染病的常用数学模型, 其将传染病流行范围内的人群分为不同的类型, 使用微分方程刻画几类人群数量的变化关系[1].借助于该数学模型, 一方面, 可以研究稳定性等模型本身的数学特性; 另一方面, 可以结合最优控制方法, 从而制定有效的传染病防治策略[2].
接种疫苗是防治传染病的常用手段.而在实际的疫苗接种策略制定时,疫苗接种行为通常会受到额外的限制.文献[3]考虑了可用疫苗总量有限的情况下某SEIR模型的最优疫苗接种策略.使用与文献[3]同样的SEIR模型,文献[4]考虑了疫苗生产能力受限情况下的最优疫苗接种策略.除了疫苗相关的约束,文献[4]还对易感染人口数施加了约束,以保证其在整个控制过程中低于一定数值,在一定程度上限制传染病的流行.从上述讨论中可以发现,在制定疫苗接种策略时,通常会导致一个含有不同类型约束的最优控制问题.
传染病的传播特性往往随着时间的推移产生变化,因此,一部分学者选择采用时变系统描述传染病的动力学特性.文献[5]基于季节性变化的SIR模型研究了流感类传染病的疫苗接种和治疗策略;更具一般性地,文献[6]将传染率定义为时间、易感染人口数、感染人口数和总人口数的非线性函数.而在使用疫苗对抗疾病的过程中,病原体可能对疫苗产生抗药性,导致成功免疫率随时间的推移而下降[7].文献[8]讨论了疟原虫的抗药性及其对疟疾控制策略制定的影响.除了传染病本身可能具有的时变特性,疫苗产量也可能具有时变特性,这对新型爆发的传染病更为显著.具体地,某新型传染病爆发缓慢初期,相应疫苗的研制工作通常进展缓慢,导致疫苗生产能力较低.而随着对该传染病研究的深入,疫苗生产能力将会逐渐增加.从上述讨论中可以发现,在抗击传染病的疫苗接种策略规划中,需要尽可能完善地考虑时变因素以服务真实情况.
尽管经典的SEIR模型中设立了潜伏仓室,但微分方程中不存在任何时滞量,即模型并不能体现潜伏期的特性.为此,一些学者考虑使用时滞微分方程建立传染病模型.文献[9]研究了含有垂直传染和脉冲免疫的时滞SEIR模型的全局动力学行为.从时滞的存在方式上来说,潜伏期的时滞本质上属于状态时滞.同时,在控制问题当中,控制时滞也是一种常见的时滞引入方式.文献[10]基于时滞SIR模型考虑了H1N1型流感的最优疫苗接种策略,其中考虑了疫苗起效的延迟.在经典的仓室模型中引入时滞因素可以更加真实地描述传染病的传播规律,但也在一定程度上给相应控制策略的求解带来了挑战.
本文在经典SEIR模型的基础上,考虑对易感染人群接种疫苗,并引入时变的感染率和时变的成功免疫率,使用时滞参数描述潜伏期,构造了含有时滞的时变受控SEIR模型.进一步地,基于该模型构造了以疫苗接种率为控制变量的最优控制问题.除了控制量本身受限于特定区间内,一方面,对易感染人口数施加了上限约束;另一方面,考虑疫苗具有时变的产量限制.同时,使用文献[11]中发展的多区段保辛伪谱方法求解该最优控制问题,数值结果表明,在满足各种约束的条件下,制定的控制策略可以有效地抑制传染病的传播.本文工作可以为传染病疫苗接种策略的制定提供借鉴.
1 SEIR模型描述
1.1 经典SEIR模型
经典的SEIR仓室模型,将总人口分为4个仓室,即易感染人群(S)、潜伏人群(E)、感染人群(I)和康复人群(R).具体地:S仓室中的个体未被感染但容易被感染;E仓室中的个体已被感染但尚不具有传染力;I仓室中的个体已经染病并具备传染力;R仓室中的个体已经被治愈或未染病并具有免疫力.所有新生个体都进入S仓室.S仓室中的个体接触I仓室中的个体,有一定概率被感染.令S(t),E(t),I(t)和R(t)分别代表相应仓室中在t时刻的个体数目.则在t时刻,所有仓室中个体数目的总和可以记作N(t)=S(t)+E(t)+I(t)+R(t).
为了刻画疾病在特定种群内的传播,令b和d分别代表自然出生率和自然死亡率,e代表潜伏个体转化为感染个体的概率,g代表感染个体康复的概率,a代表疾病导致的死亡率,c代表传染系数.则经典的SEIR模型可以写作
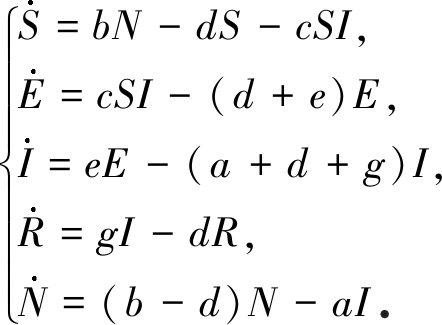
(1)
由式(1)可知,经典的SEIR模型为一自治系统,即系统中不含有任何时变参数.
1.2 含有时滞的时变受控SEIR模型
在本文中,假设参数a,b,d,e,g在整个控制时长内为常数,而传染系数c为如下季节性变化的参数:
c(t)=c0+c1cos(2πt+φ0),
(2)
其中c0>0和c1≥0分别为传染系数的均值和幅值,φ0∈[0,2π)为初始相位.
令变量u代表S仓室中个体接种疫苗的比例.此外,假设每个接种的个体获得免疫的概率为f(t),即在t时刻有u(t)S(t)个个体接种了疫苗,然而其中仅有f(t)u(t)S(t)个个体成功获得免疫.考虑病原体的抗药性,成功免疫率可以表示为如下时变函数:
f(t)=f0+f1exp(-t/f2),
(3)
其中f0, f1, f2为非负参数.从式(3)中可以发现, f(0)=f0+f1且limt→∞ f(t)=f0.
同时,为了刻画潜伏期,认为在t时刻,由S仓室进入E仓室中的个体数为c(t)S(t-τ)I(t-τ)而并非经典模型中的c(t)S(t)I(t),其中参数τ为传染病的潜伏期.
通过对上述控制因素、时滞因素和时变因素三方面的改进,可以得到如下的含有时滞的时变受控SEIR模型:
(4)
(5)
(6)
(7)
(8)
图1给出了对应的仓室模型图.
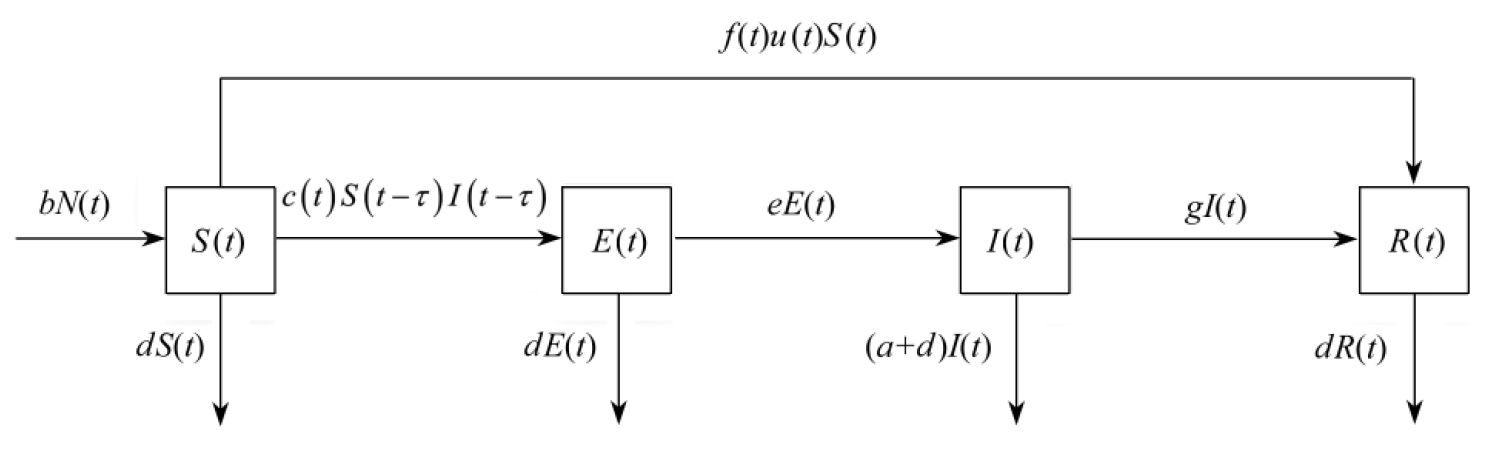
图1 含有时滞的时变受控SEIR仓室模型图
Fig. 1 The diagram of the time-varying controlled SEIR compartmental model with delay
相比于经典的SEIR模型,本文提出的受控模型中含有时滞和时变两方面的因素,可以更真实地模拟传染病的传播规律.但在该模型中仅将传染系数改进为时变参数,在实际应用中,可以根据对传染病传播规律的分析,选取合适的参数改进方式和时滞引入方式.
2 控制问题描述
2.1 最优控制问题列式
在式(4)S仓室相关的动力学方程中,由于变量u本身代表了易感染人群的疫苗接种率,其自然地存在于区间[0,1]当中.然而在实际情况中,接种率的上限可能并不能达到1,因此在本文中对接种率施加如下约束:
0≤u(t)≤umax.
(9)
根据实际情况,疫苗的产量应该服从如下约束:
u(t)S(t)≤Ω(t),
(10)
其中Ω(t)为时变函数,代表在t时刻疫苗的产量上限.
此外,对易感染人口数施加如下的边界约束,以更好地抑制疾病的传播:
S(t)≤Smax,
(11)
其中Smax∈R+代表了控制方案中设定的易感染人口数上限.
观察式(4)~(8)中的5个微分方程,有一个是冗余的.在最优控制问题的构造时,不妨选取状态空间为x=[S E I N]T.同时,将疫苗接种率u(t)作为控制变量.而在性能指标中,需要同时考虑疫苗消耗量和感染人口数两方面的因素,因此不妨将性能指标取做感染人口数和接种率的加权二次型.基于上述假设,可以将最优疫苗接种问题转化为如下终端自由的最优控制问题:
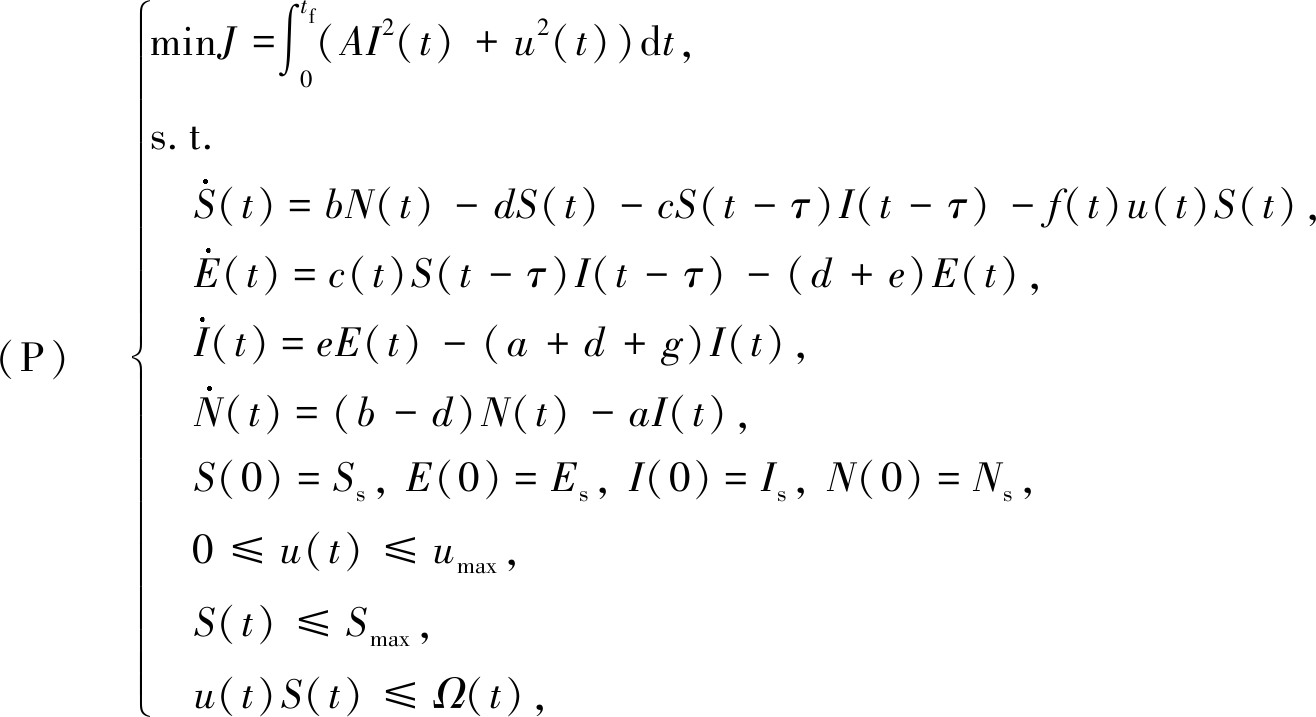
(12)
其中,假设控制从t=0时刻开始,tf∈R+为对应控制的终止时刻;A∈R+为性能指标中感染人口数的权值.
为统计接种疫苗的人数,引入新的变量V(t),其满足
(13)
由于在问题(P)中不对接种疫苗的总人数施加限制,因此没有必要将变量V(t)计入状态空间.但是,若考虑疫苗总量的约束,则应类似于文献[3]将变量V(t)计入状态空间.
2.2 数值求解方法
从列式中可以看出,问题(P)其实是一个时滞微分方程的最优控制问题,且包含了纯控制约束、控制-状态混合约束和纯路径约束.使用变分法或Pontryagin极大值原理求解该问题将会遇到极大困难,因此需要选择合适的数值方法进行求解.实际上,最优控制问题可以通过变分原理导入Hamilton系统[12],而保辛方法可以高效地求解Hamilton系统[13].尤其是对于时间区间较长的问题,保辛方法相比非保辛方法可以提供更精确的数值结果[14].而在疫苗接种策略的规划中,通常考虑数月甚至数年的时间跨度.因此,本文在求解最优控制问题时,采用了文献[11]发展的多区段保辛伪谱算法.
3 数 值 仿 真
3.1 系统参数说明
本节将讨论几种不同算例下的最优疫苗接种策略.在每种算例中,若不特殊指出,系统参数的选取如表1所示.
表1 仿真中默认的系统参数
Table 1 The default system parameters

parameterparameter descriptionvalueadisease induced death rate0.2bnatural birth rate0.525cincidence coefficient0.001dnatural death rate0.5eexposure rate to infection0.5fsuccessfully immune rate1ginfection to recovery rate0.1τlatent delay1/12Aweight on the infectious population0.002tfnumber of years15Ssinitial susceptible population1 000Esinitial exposed population100Isinitial infectious population50Rsinitial recovered population15Nsinitial total population1 165umaxmaximum vaccination rate1Smaxmaximum susceptible population1 100Ωmaximum vaccination supply at each moment1 000
在使用文献[11]中多区段保辛伪谱算法求解不同情况中的问题时,均将子区间长度固定为τ,即将整个求解域离散成tf/τ=180个等长的子区间,且每个子区间内采用5阶LGL型伪谱方法,收敛误差设为ε=10-6.
3.2 数值算例
3.2.1 算例1:无时变参数
在算例1中,系统参数完全按照表1选择,即不考虑任何时变因素的影响,仿真结果在图2中给出.可以发现,在计算得到的控制策略下,潜伏个体数和感染个体数相较于无控情况下可以更快速地降低.在无控情况下,由于对易感染个体数未做任何约束,其从初始时刻开始即保持增加;然而在有控情况下,易感染个体数在短暂的降低后开始增加,但并未超过设定的上限Smax.
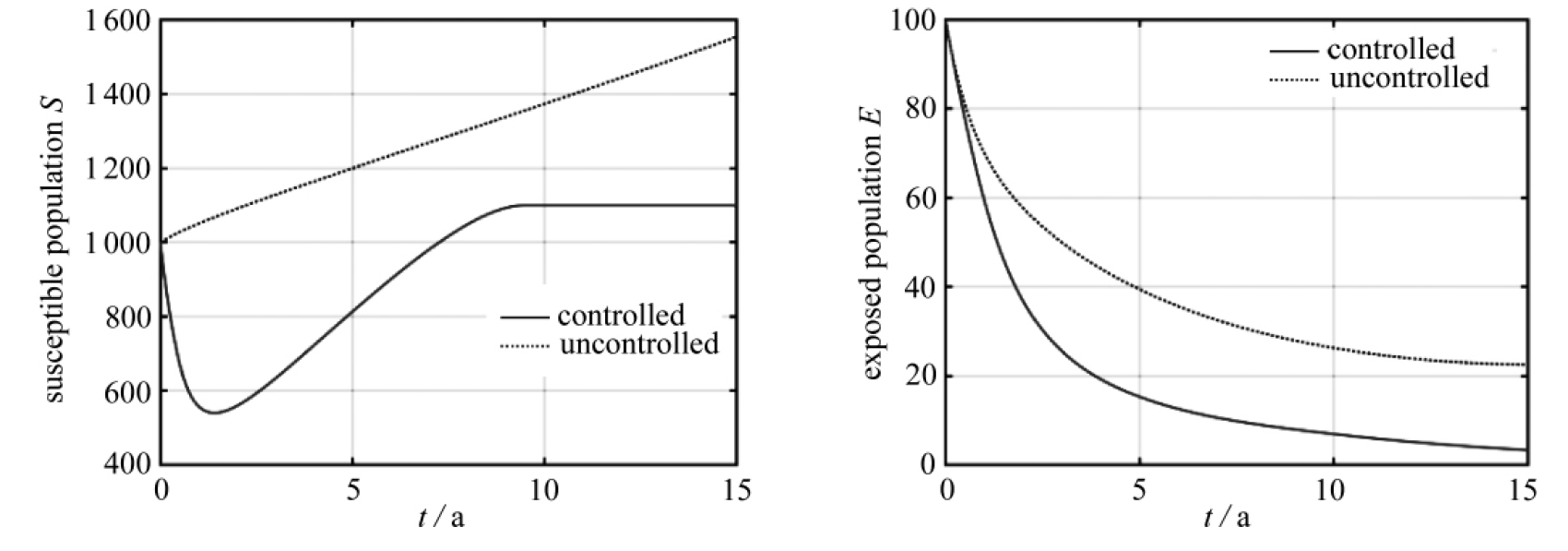
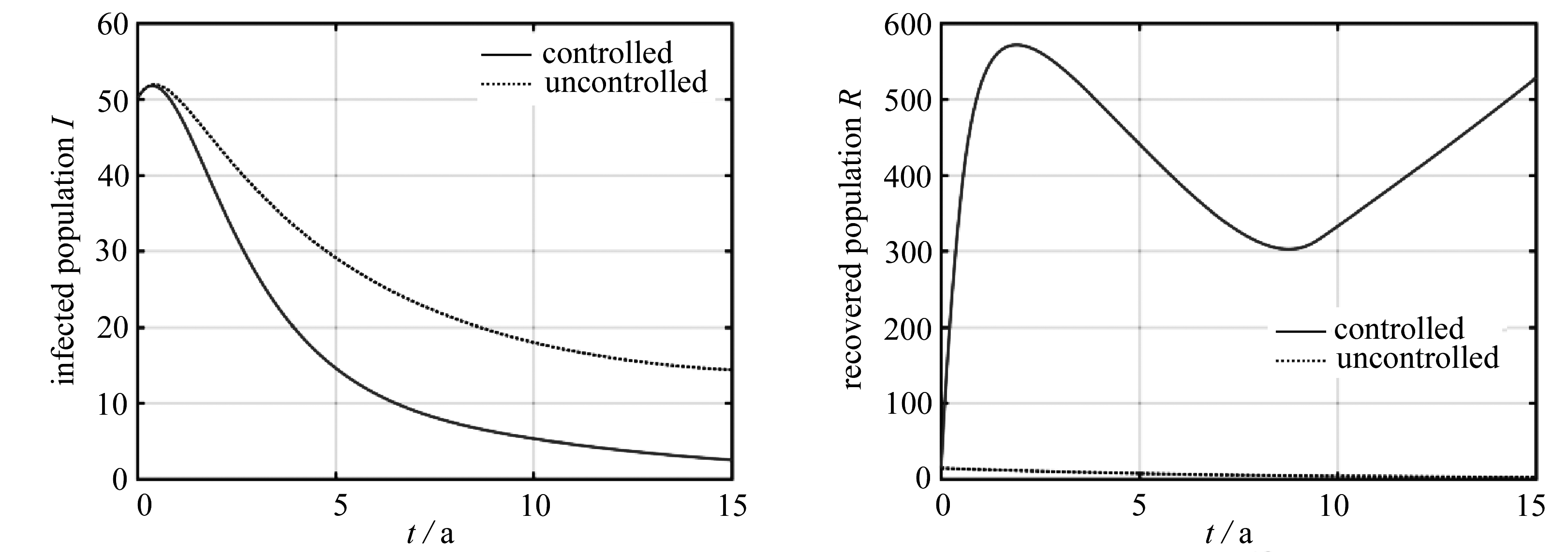
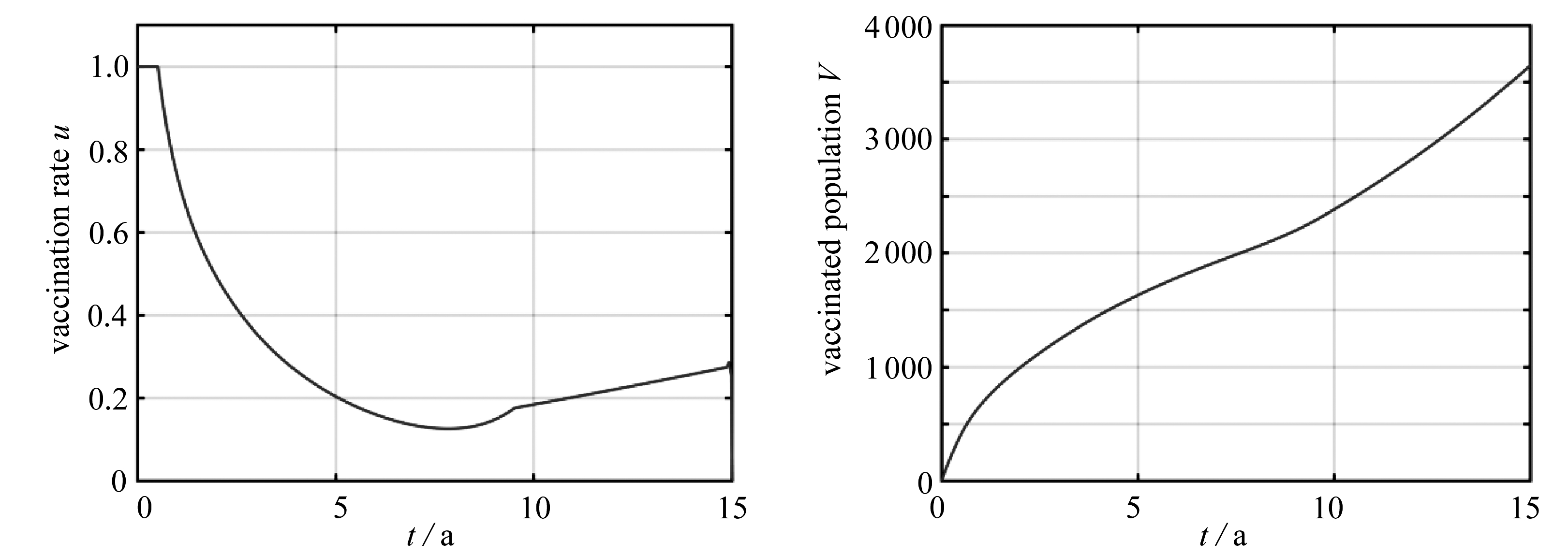
图2 算例1:最优状态轨迹、最优疫苗接种率以及接种疫苗人数
Fig. 2 Case 1: optimal state trajectories, optimal vaccination rates and vaccinated populations
3.2.2 算例2:考虑季节性变化的传染系数
在算例2中,考虑传染系数为如下季节性变化的函数,并在图3中给出了仿真结果.
c(t)=0.001+0.000 5cos(2πt).
(14)
从图3可以发现,无论是在有控还是无控情况下,状态变量和控制变量都存在振荡的特性.且该算例中有控情况下状态变量和控制变量的变化趋势和算例1完全相同.
3.2.3 算例3:考虑随时间降低的成功免疫率
在算例3中,由于抗药性的存在,考虑成功免疫率为如下单调递减的函数,并在图4中给出了仿真结果.
f(t)=exp(-t/50).
(15)
该算例状态变量和控制变量的变化趋势和算例1相似,但相对于算例1,控制输出有了明显的增加.
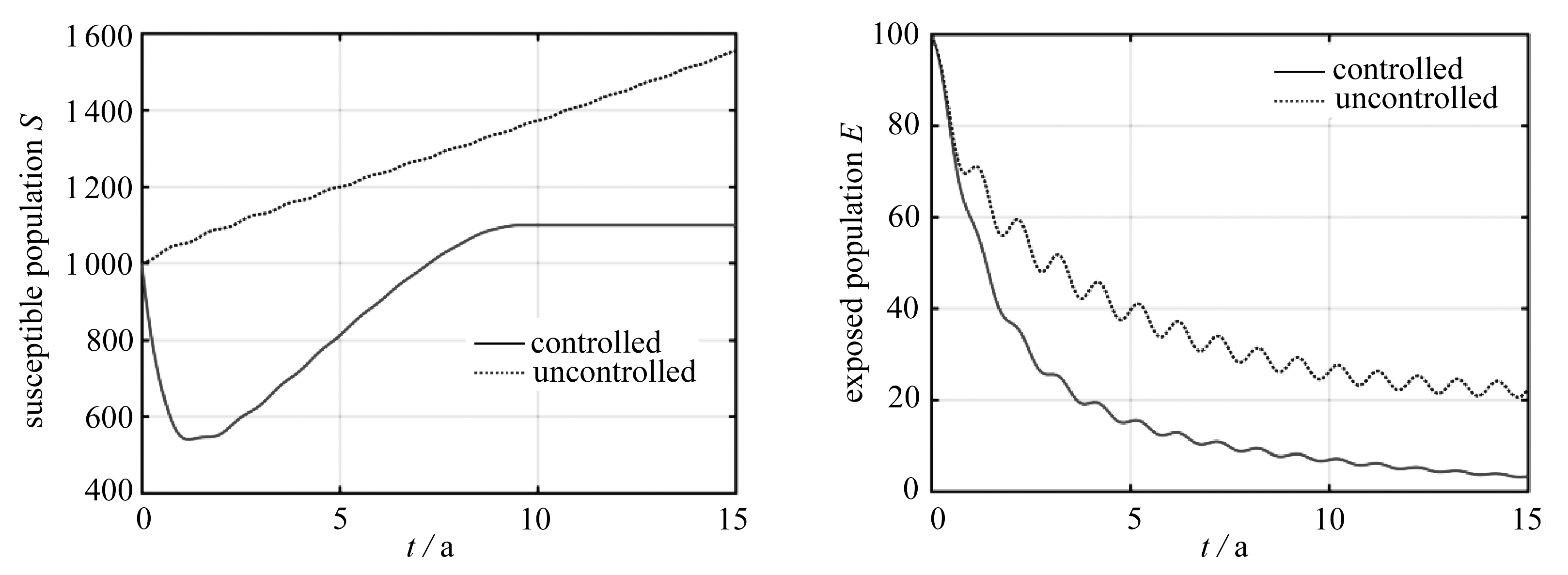
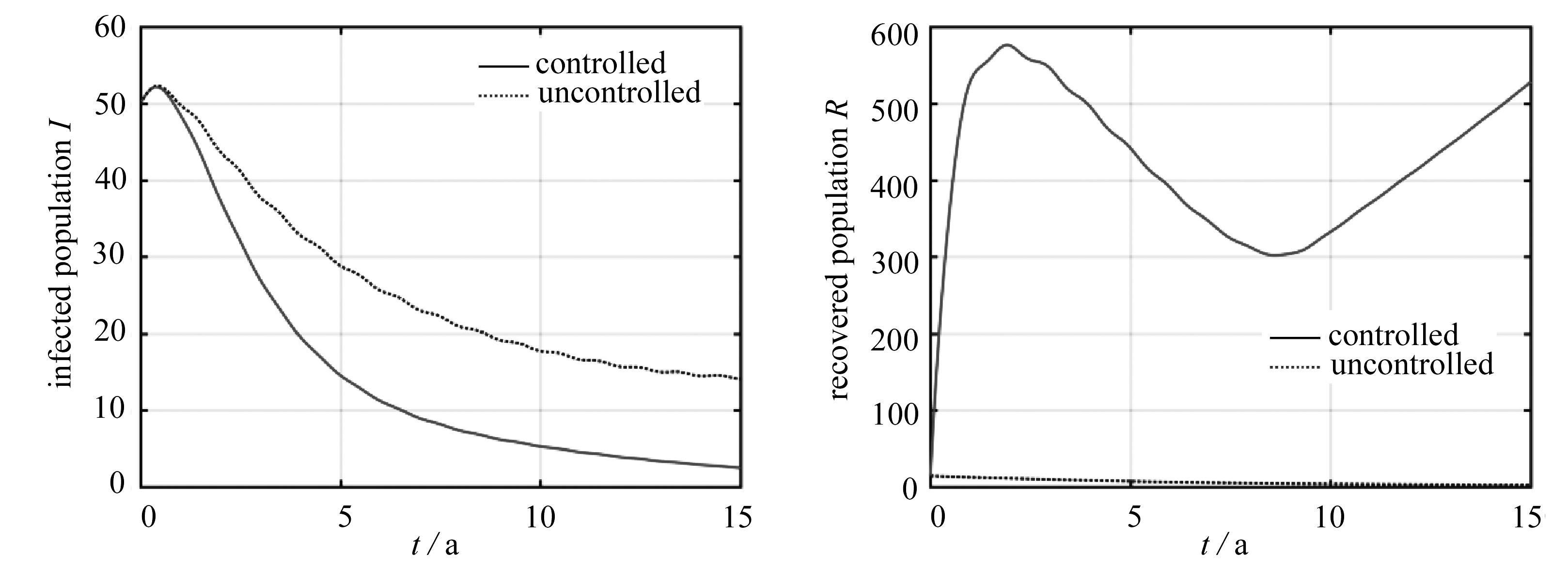
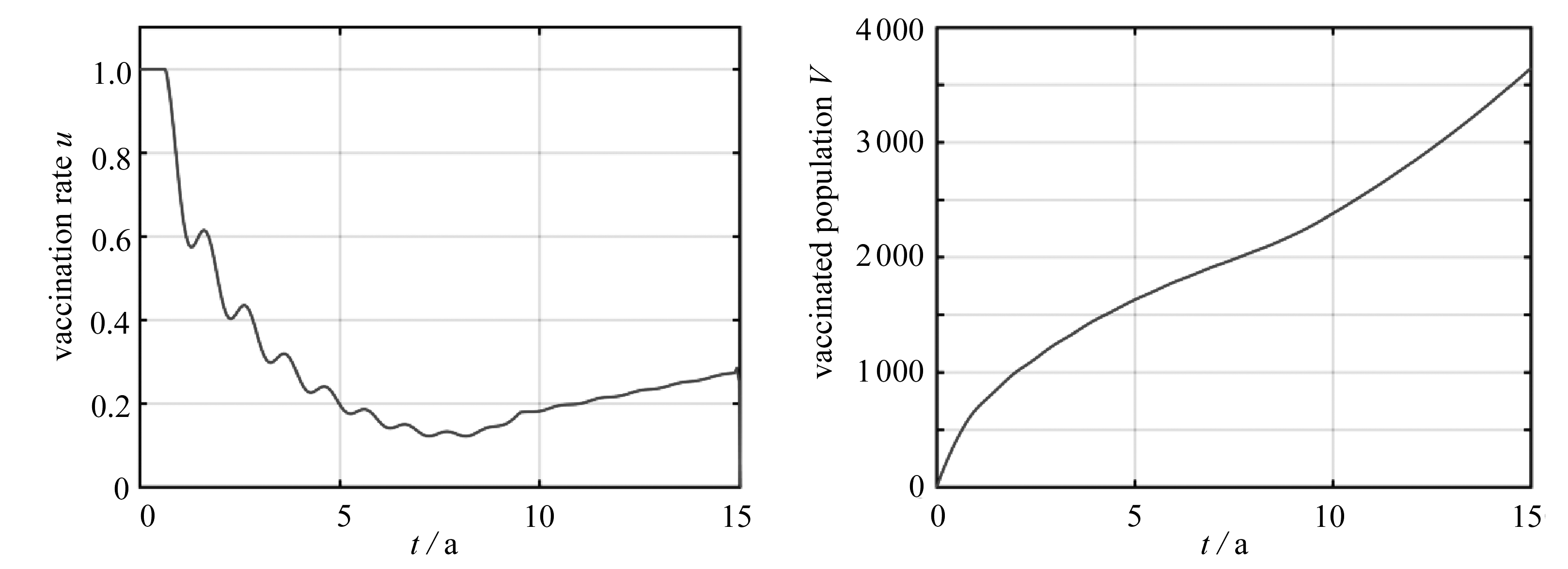
图3 算例2:最优状态轨迹、最优疫苗接种率以及接种疫苗人数
Fig. 3 Case 2: optimal state trajectories, optimal vaccination rates and vaccinated populations
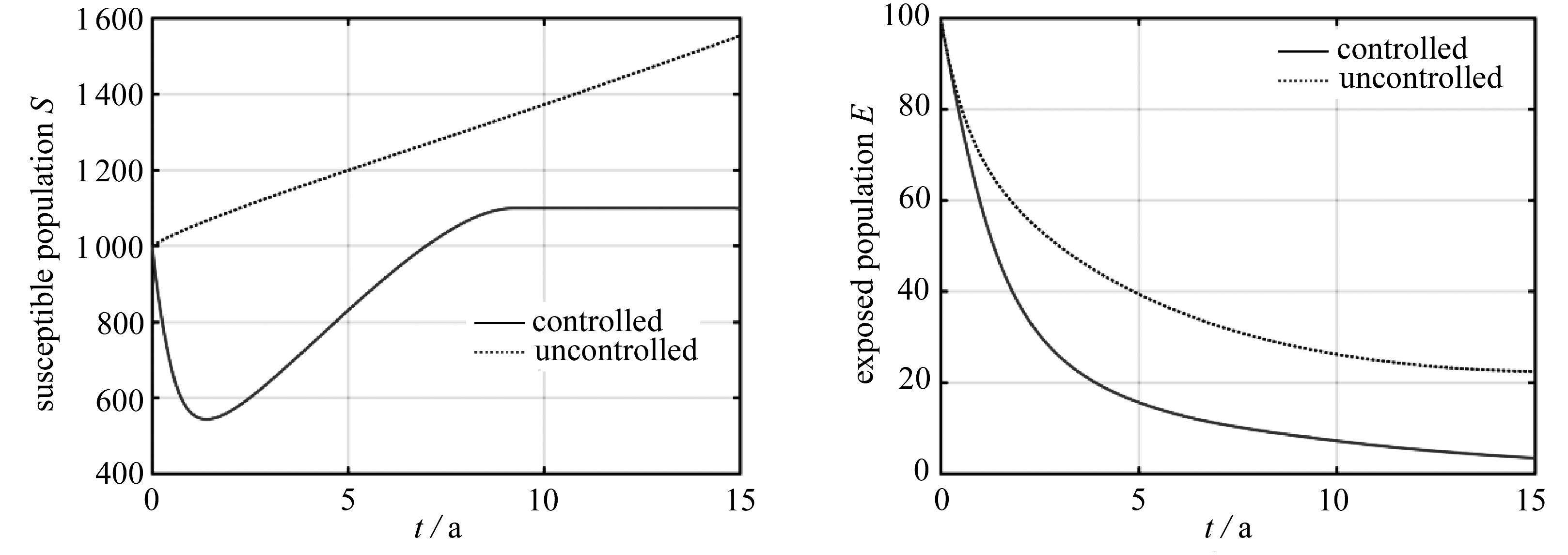
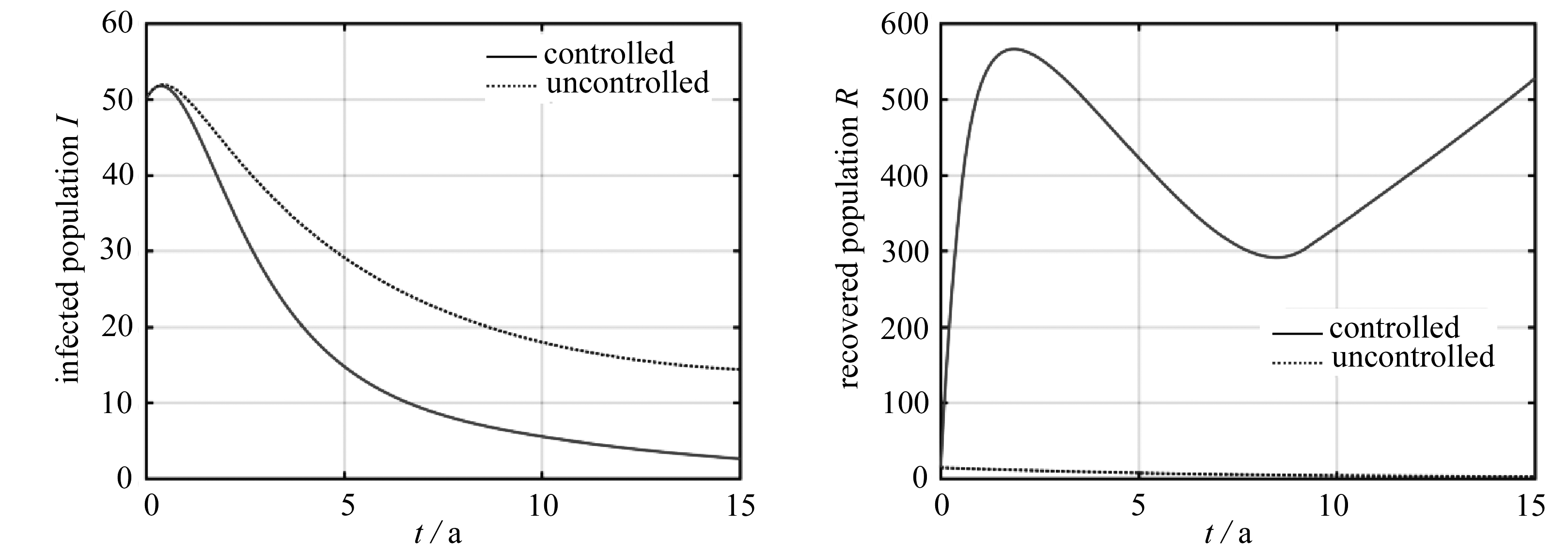

图4 算例3:最优状态轨迹、最优疫苗接种率以及接种疫苗人数
Fig. 4 Case 3: optimal state trajectories, optimal vaccination rates and vaccinated populations
3.2.4 算例4:考虑随时间增长的疫苗产量
在算例4中,对新型爆发的传染病,考虑疫苗产量为如下单调递增的函数,并在图5中给出了仿真结果.
Ω(t)=1 000-900exp(-t/5).
(16)
在初始时刻,本算例中疫苗产量处于较低水平,因此疫苗接种率也被迫保持在较低水平,从而与算例1~3中的控制变量呈现了截然不同的变化趋势.
3.2.5 算例5:同时考虑3.2.2~3.2.4三类时变因素
在算例5中,为模拟更加复杂的情况,同时考虑式(14)~(16)中的时变因素,仿真结果在图6中给出.
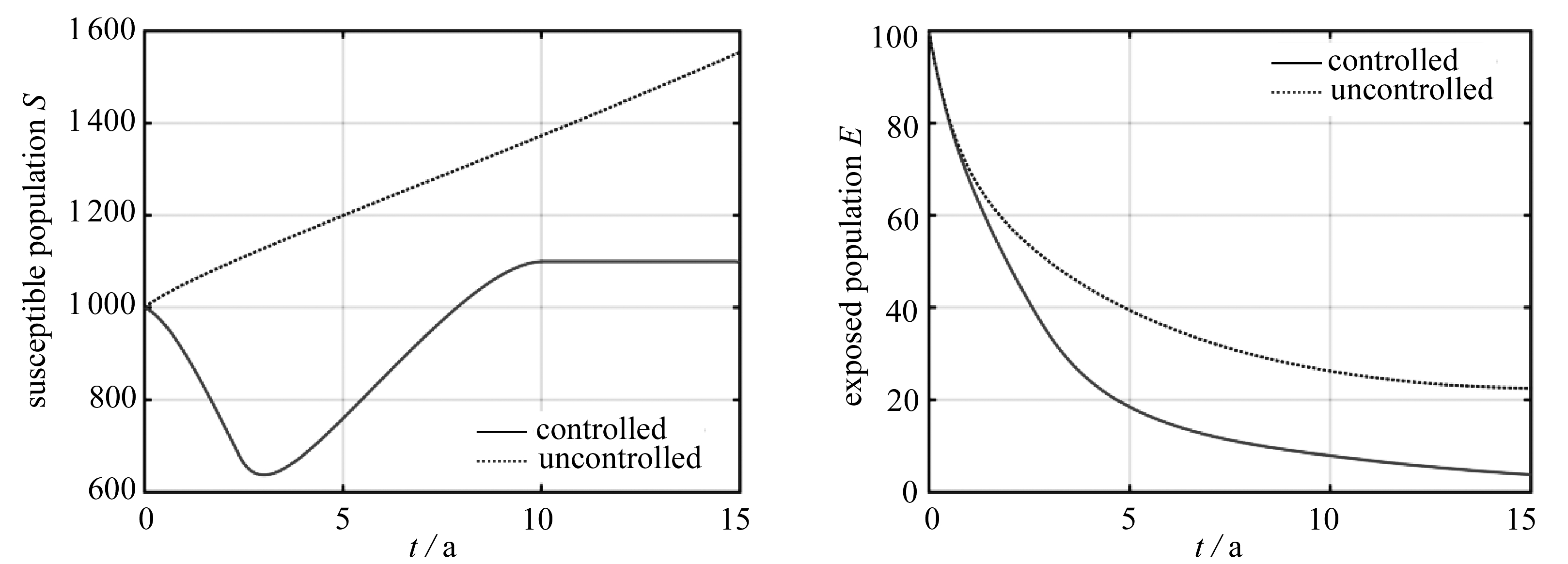
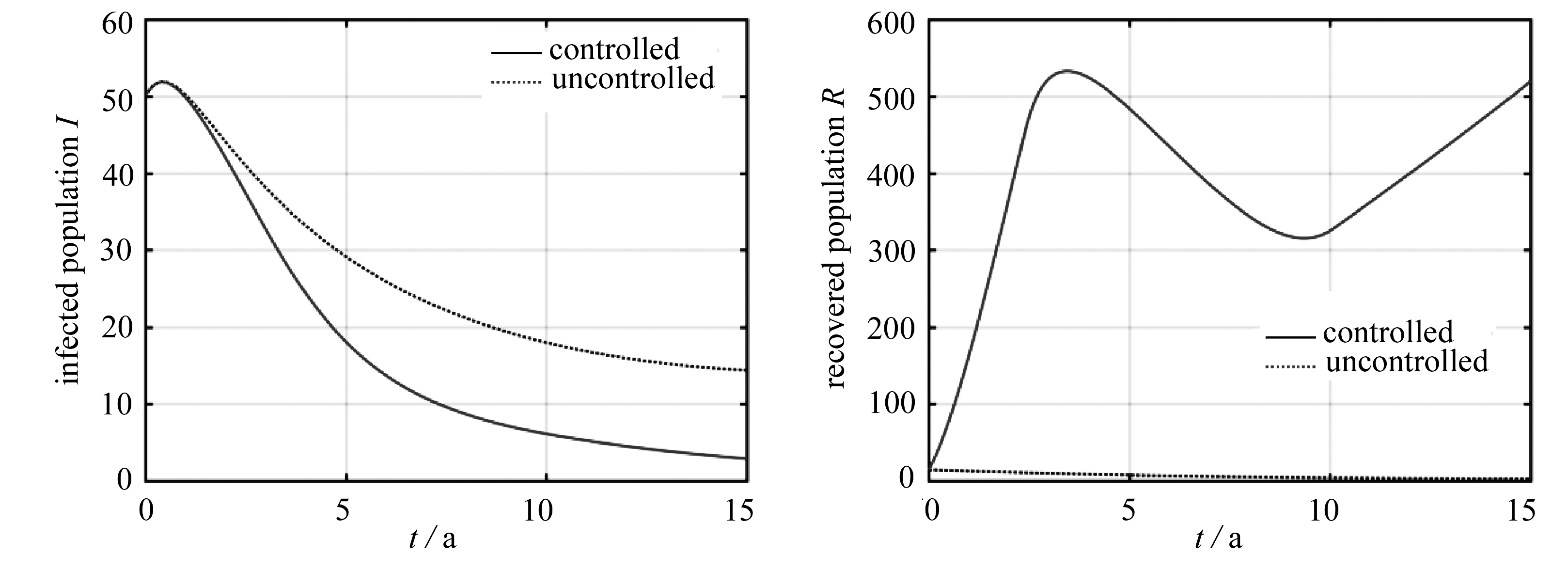

图5 算例4:最优状态轨迹、最优疫苗接种率以及接种疫苗人数
Fig. 5 Case 4: optimal state trajectories, optimal vaccination rates and vaccinated populations
3.3 结果分析
从图2~6中的结果可以发现,对于给出的5个算例,均能通过接种疫苗有效控制传染病的传播,且几类约束均得到严格的满足.
为了进一步讨论时变因素对最优疫苗接种策略的影响,在图7(a)和图7(b)中,分别绘制了5个算例中的控制变量和疫苗接种人数;并且在表2中,对5个算例中的性能指标、状态变量终端值等做了总结.这里需要注意,当不施加控制时,算例1,3,4得到同样的结果,算例2,5得到同样的结果.
当在算例2中引入季节性改变的传染系数后,无论是状态变量或是控制变量,都呈现明显的振荡特性,但是变量的变化趋势、性能指标和接种疫苗人数,都与算例1中大体相同.
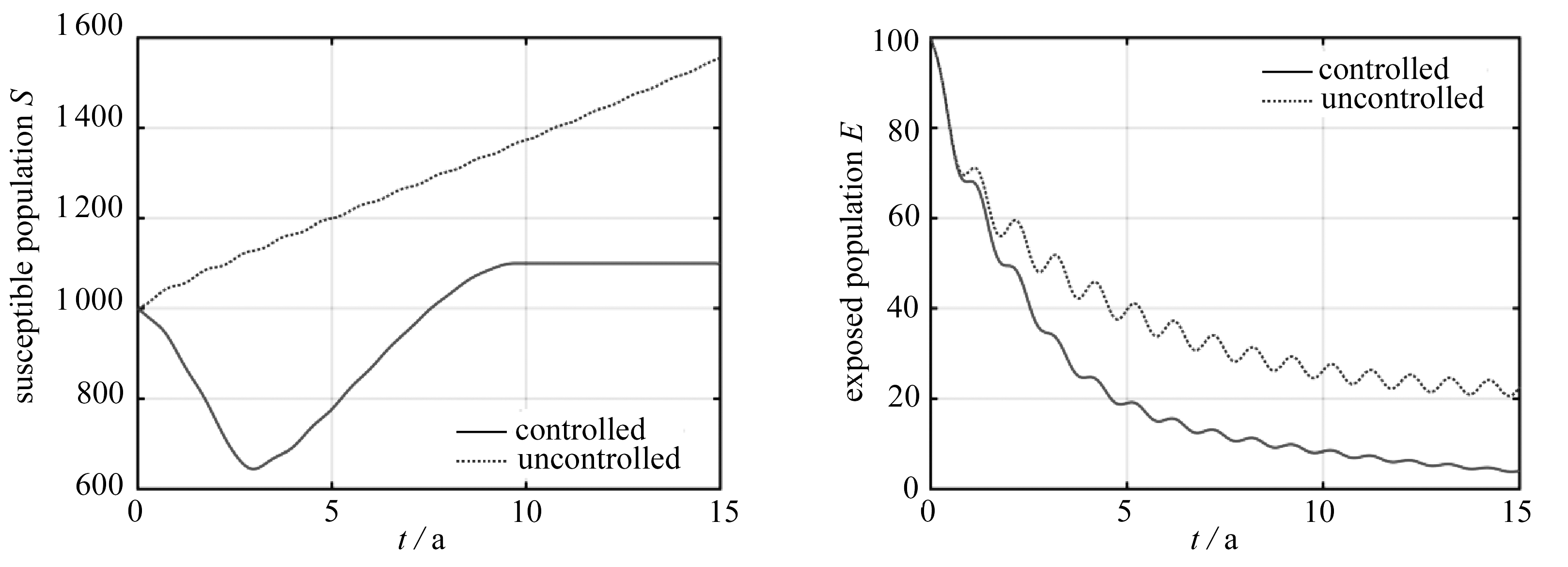
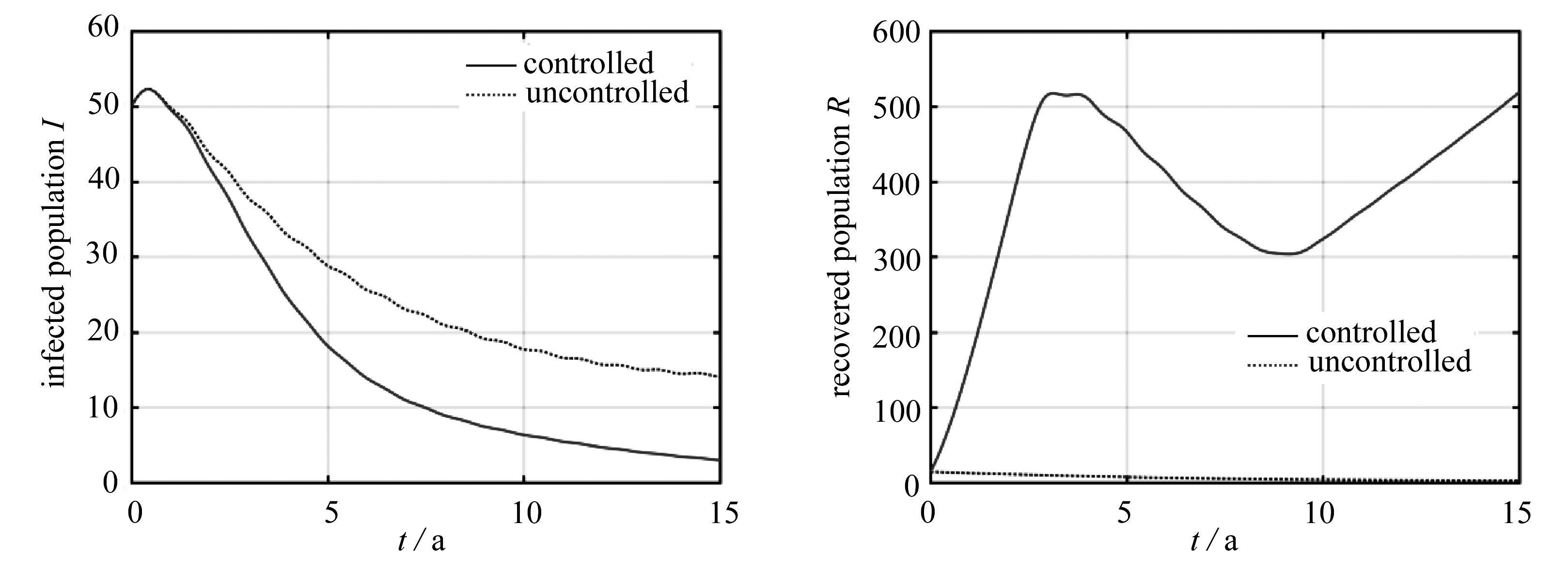
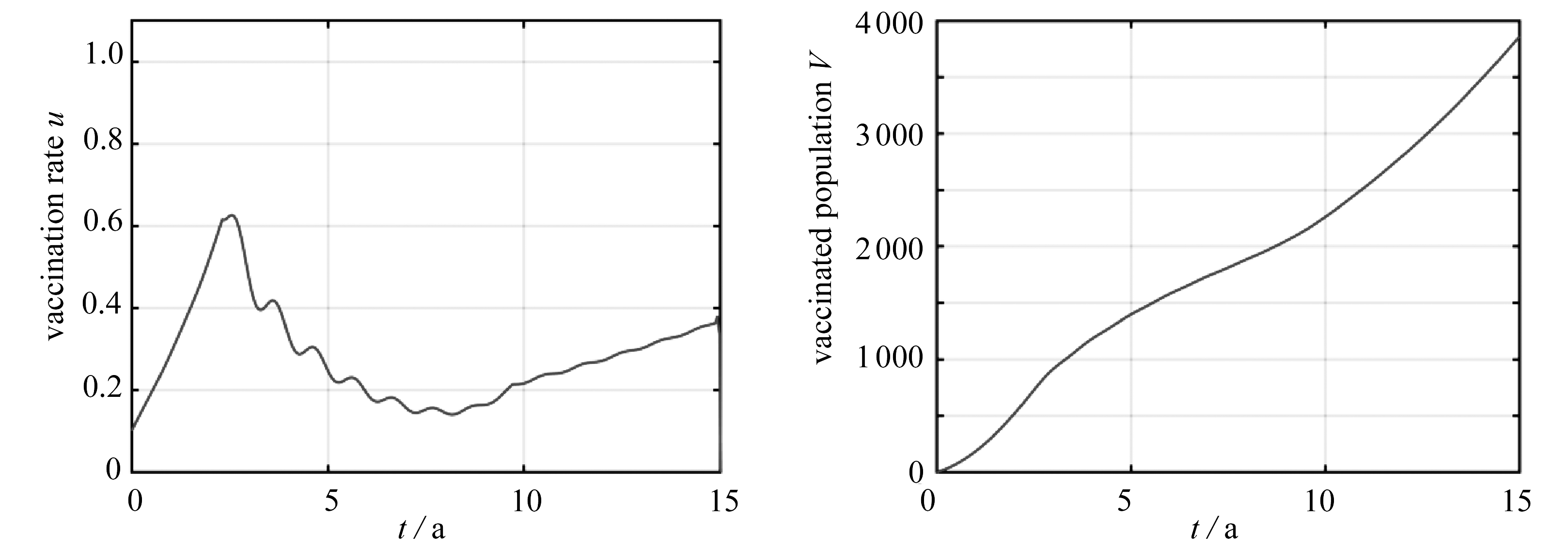
图6 算例5:最优状态轨迹、最优疫苗接种率以及接种疫苗人数
Fig. 6 Case 5: optimal state trajectories, optimal vaccination rates and vaccinated populations
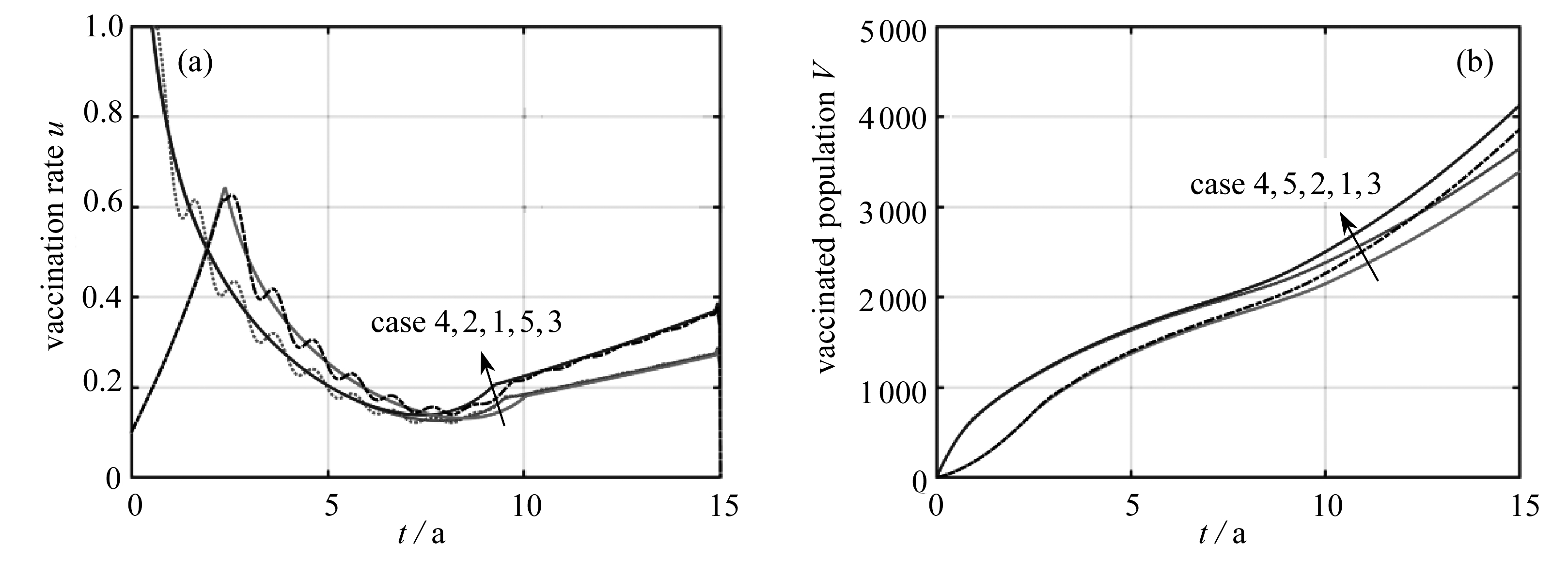
图7 5个算例中的控制变量和疫苗接种人数
Fig. 7 Control variables and vaccinated populations in 5 cases
表2 不同算例中性能指标和状态变量终端值
Table 2 Performance indices and final state values in 5 cases

case №.S(tf)E(tf)I(tf)R(tf)N(tf)V(tf)performance indexuncontrolled1,3,41 55422.5014.693.151 594025.292,51 55422.5714.183.121 594025.13controlled11 1003.342.56528.401 6343 64715.5921 1003.342.52528.431 6343 64615.6231 1003.482.66527.631 6344 12815.8841 1003.812.91520.081 6273 39117.4151 1004.013.02519.141 6263 86217.74
当在算例3中引入单调递减的成功免疫率后,有更多的个体接种了疫苗.虽然算例3中的控制变量和算例1中具有相同的趋势,但是两者之间存在越来越大的差异.此外,算例3中的性能指标也要大于算例1.
在算例1~3中,控制变量在初始阶段均保持在1的位置.然而,在算例4中,控制变量在初始阶段从一个较低的水平开始增长.这是因为在算例4中,假设了疫苗的产量在初期处于较低的水平,从而为了满足式(16)中关于疫苗产量的约束,控制变量被迫保持在较低的水平.在增长到了某个时间点后,控制变量开始下降,并呈现出和算例1中类似的趋势,这可以理解为疫苗的产量达到了和算例1中近似的水平.上述原因也导致了相较于算例1,算例4中更少的个体接种疫苗.
在5个算例中,相对于无控情况,有控情况最终进入到康复仓室中的个体数均大幅地增加,且在控制终止时刻人口总数也有一定增长.从上面5个算例的对比可以发现,当引入了时变因素后,都会或多或少地在一定程度上改变最优的疫苗接种策略.这表明忽略时变因素,会导致不合理的控制策略.同时,本文的算例也在一定程度上启发了我们,可以从如下3个方面入手,提高疫苗接种策略的科学性: 1) 对传染病传播的动力学建立精确的模型; 2) 对病原体的抗药性进行量化分析; 3) 对国内医药企业疫苗研制、生产能力要有清晰的认识.
4 结 论
本文在经典SEIR传染病模型的基础上,通过引入时变和时滞两方面的因素,建立了含有状态时滞的时变SEIR模型.以疫苗接种率作为控制量,考虑疫苗产量、种群人口上限等约束,建立最优控制问题.通过多区段保辛伪谱方法求解,得到了考虑不同时变因素下的最优疫苗接种策略.数值结果表明在最优控制问题的框架下, 计算得到的疫苗接种策略可以有效控制传染病的传播.本文工作凸显了时变因素的影响, 对新型传染病的疫苗接种策略具有一定借鉴意义.
[1] KERMACK W O, MCKENDRICK A G. A contribution to the mathematical theory of epidemics[J]. Bulletin of Mathematical Biology, 1991, 53(1/2): 33-55.
[2] ANDERSON R M, MAY R M. Infectious Diseases of Human: Dynamics and Control[M]. Oxford: Oxford University Press, 1992.
[3] NEILAN R M, LENHART S. An introduction to optimal control with an application in disease modeling[J]. DIMACS Series in Discrete Mathematics, 2010, 159(40): 67-81.
[4] BISWAS M H A, PAIVA L T, DE PINHO M. An SEIR model for control of infectious diseases with constraints[J]. Mathematical Biosciences and Engineering, 2014, 11(4): 761-784.
[5] LEE S, CHOWELL G. Exploring optimal control strategies in seasonally varying flu-like epidemics[J]. Journal of Theoretical Biology, 2017, 412: 36-47.
[6] MATEUS J P, REBELO P, ROSA S, et al. Optimal control of non-autonomous SEIRS models with vaccination and treatment[J]. Discrete and Continuous Dynamical Systems, 2018, 6: 1179-1199.
[7] JACKSON T L, BYRNE H M. A mathematical model to study the effects of drug resistance and vasculature on the response of solid tumors to chemotherapy[J]. Mathematical Biosciences, 2000, 164(1): 17-38.
[8] OKOSUN K O, MAKINDE O D. Modelling the impact of drug resistance in malaria transmission and its optimal control analysis[J]. International Journal of Physical Sciences, 2011, 6(6): 6479-6487.
[9] 孟新柱, 陈兰荪, 宋治涛. 一类新的含有垂直传染与脉冲免疫的时滞SEIR传染病模型的全局动力学行为[J]. 应用数学和力学, 2007, 28(9): 1123-1134.(MENG Xinzhu, CHEN Lansun, SONG Zhitao. Global dynamics behaviors for a new delay SEIR epidemic disease model with vertical transmission and pulse vaccination[J]. Applied Mathematics and Mechanics, 2007, 28(9): 1123-1134.(in Chinese))
[10] ELHIA M, RACHIK M, BENLAHMAR E. Optimal control of an SIR model with delay in state and control variables[J]. ISRN Biomathematics, 2013. DOI: 10.1155/2013/403549.
[11] WANG X, PENG H, ZHANG S, et al. A symplectic local pseudospectral method for solving nonlinear state-delayed optimal control problems with inequality constraints[J]. International Journal of Robust and Nonlinear Control, 2017, 28(6): 2097-2120.
[12] BRYSON A E, HO Y C. Applied Optimal Control[M]. Wiley, 1975.
[13] FENG K, QIN M. Symplectic Geometric Algorithms for Hamiltonian Systems[M]. Berlin: Springer, 2010.
[14] 钟万勰. 应用力学的辛数学方法[M]. 北京: 高等教育出版社, 2006.(ZHONG Wanxie. Symplectic Solution Methodology in Applied Mechanics[M]. Beijing: Higher Education Press, 2006.(in Chinese))