引 言
混沌作为非线性科学中一种特有的复杂现象,其理论研究与实际应用已成为非线性科学领域的研究热点及重点.著名的Lorenz系统是首个被提出的混沌系统,它是由Lorenz于1963年在分析大气对流模型所对应的三维方程组时,运用数值计算方法发现的.Lorenz系统的解对初始值敏感依赖,这意味着初始值的小扰动会随着时间的延续对最终的结果产生巨大影响,此性质被Lorenz形象地解释为“蝴蝶效应”.而忆阻器自提出并证实以来, 因其非线性的特性,被广泛应用在混沌系统中.带有忆阻器的混沌系统具有更加复杂的动力学行为,且更具初始条件敏感性[1],因此在图像加密[2]、 保密通信[3]等领域有着广泛的应用前景.
文献[4]提出了一种新型浮地忆阻器混沌电路[5],分析了其基本动力学特性和Hopf分岔,并且证明在初始条件改变时,能产生共存吸引子和混沌吸引子与周期极限环共存现象,但没有对其高余维分岔[6]进行分析.在文献[7] 中,笔者对带有忆阻器的Lorenz型系统的Pitchfork分岔以及Hopf分岔等余维一分岔进行了分析.而在本文中,我们将研究zero-Hopf分岔(zero-Hopf平衡点是指具有一个零特征值以及一对纯虚特征值的孤立平衡点,其余特征值都有非零实部)和double-zero分岔(double-zero平衡点是指具有两个零特征值,其余特征值都有非零实部)等高余维分岔行为,以及系统在无穷远处的动力学行为.研究的系统如下:
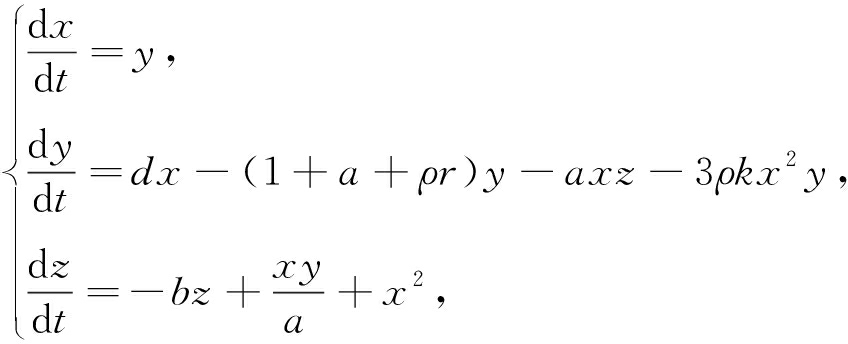
(1)
其中参数a,b为原Lorenz系统中的参数,d为原Lorenz系统参数中的a(c-1),r,k为忆阻器模型参数,ρ为忆阻器强度参数,且满足ρ>0.当参数条件为a=10.47,b=3.61, d=192.64, k=-0.02, ρ=1.25, r=0.36,初值条件为x=0.1, y=0, z=0时,系统为混沌状态,其相图如图1所示.该混沌吸引子对应的Lyapunov指数为[8]
λLE1=1.344 7, λLE2=0.000 1, λLE3=-12.185 9.
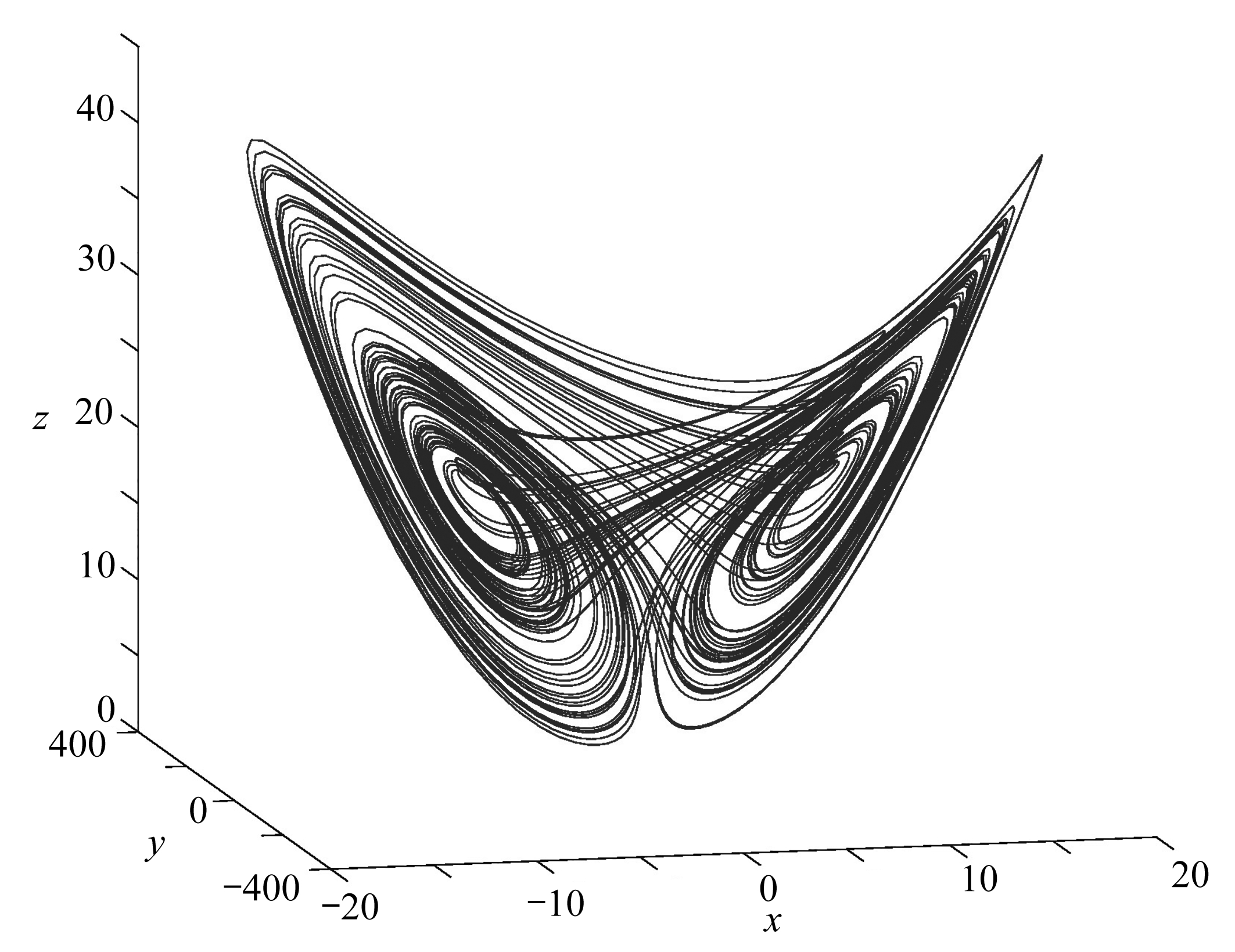
图1 系统(1)的相图
Fig. 1 The phase diagram of system(1)
1 Zero-Hopf分岔
在三维混沌系统的研究中,有很多学者研究了系统平衡点的zero-Hopf分岔现象[9-10].从这些文献可以看出, 在一定的条件下,从局部的zero-Hopf 平衡点处可以分岔出一些复杂的不变集, 也就是说, 在某些情况下, zero-Hopf平衡点的出现便意味着“混沌”的产生.因此在这一节将致力于研究系统(1)的zero-Hopf分岔,在此之前先来引入相关的概念以及定理.
考虑如下形式的微分系统:
(2)
其中ε可以任意小或充分小,且满足ε∈(-ε0,ε0),ε0>0,函数F0,F1: R×Ω→Rn,F2:R×Ω×(-ε0,ε0)→Rn是C2光滑函数,并且关于第一个变量t是T周期函数,Ω是Rn中的开子集.利用平均理论,可以研究系统(2)中T周期解的分岔问题,其主要假设是无扰动系统
(3)
有一个周期解的子流形.
假设X(t,X0)是系统(3)的周期解,且满足X(0,X0)=X0=X(T,X0),那么系统(3)沿着它的周期解的线性化系统可以重写为
(4)
记MX0(t)为线性微分系统(4)的一个基本矩阵.
假设存在一个开集V,满足cl(V)⊂Ω(cl即closure,闭包),使得每一个X0∈cl(V),有X(t,X0)是系统(3)的T周期解.cl(V)是一个仅由周期解构成的集合,它被称为系统(3)的同步集.关于包含周期解X(t,X0)的集合cl(V)的周期解分岔结论由以下定理给出.
定理1[11](同步集的扰动) 假设存在一个有界开集V,满足cl(V)⊂Ω,使得每一个X0 ∈cl(V),那么解X(t,X0)是以T为周期的,考虑函数F:cl(V)→Rn,
则有下列表达成立:
1) 如果存在X*∈V满足F(X*)=0,且det((∂F/∂X0)(X*))≠0,那么系统(2)存在一个以T为周期的解X(t,ε),且当ε→0时X(0,ε)→X*;
2) 周期解X(t,ε)的稳定性类型由Jacobi矩阵(∂F/∂X0)(X*)的特征值决定.
命题1 当b=0,a=- ρr-1,d=-ω2时,系统(1)的原点平衡点为zero-Hopf平衡点.
证明 考虑系统(1)在原点平衡点处的Jacobi矩阵为
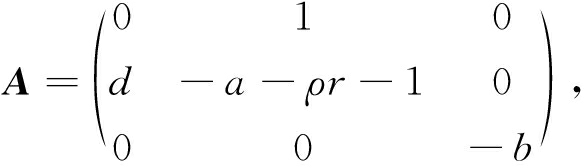
其特征多项式为
p(λ)=λ3+λ2 (a+b+ρr+1)+λ(ab+bρr+b-d)-bd.
为了使得原点平衡点为zero-Hopf平衡点,需要使
p(λ)=λ(λ2+ω2).
通过比较系数,可以得到这个等式成立的唯一条件:
b=0, a=- ρr-1, d=-ω2,
即当满足上述条件,系统(1)的原点平衡点为zero-Hopf平衡点.
在得出系统(1)存在zero-Hopf平衡点的条件后,接下来我们分析具体的分岔情况.
定理2 假设系统(1)的参数满足b=εb1, r=-(a+1)/ρ+εr1, d<0,对任意小的ε,系统(1)在原点平衡点产生的zero-Hopf分岔没有分岔出周期解.
证明 做变换b→εb1,r→-(a+1)/ρ+εr1,其中0<ε≪1,b1,r1是非零实数,系统(1)变成

(5)
进一步重新调整变量,令(x,y,z)T=(εu,εv,εw),再重新令变量(u,v,w)T=(x,y,z)T,则系统(5)变成
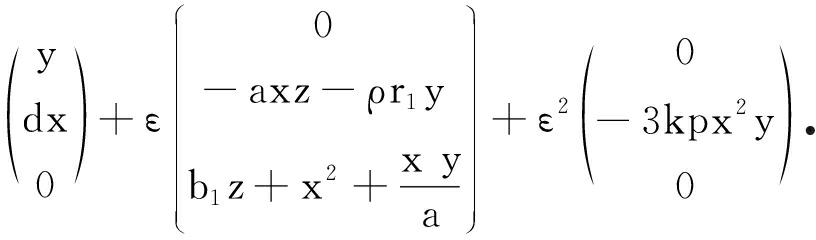
(6)
在定理1中描述的平均理论的帮助下,可以研究系统(6)的行为.考虑如下无扰动系统的初值问题:
(7)
无扰动系统(7)的解是X(t,X0)=(x(t),y(t),z(t)),其中
![]() y(t)=mx0sinh(mt)+y0cosh(mt), z(t)=z0,
y(t)=mx0sinh(mt)+y0cosh(mt), z(t)=z0,
值得注意的是, 系统(7)所有满足X0≠0的解X(t,X0)都是周期的, 且周期都为T=2π/m.沿着系统(7)的周期解X(t,X0),可以把线性化系统![]() 的基本矩阵MX0(t)写成如下形式:
的基本矩阵MX0(t)写成如下形式:

它的逆矩阵为
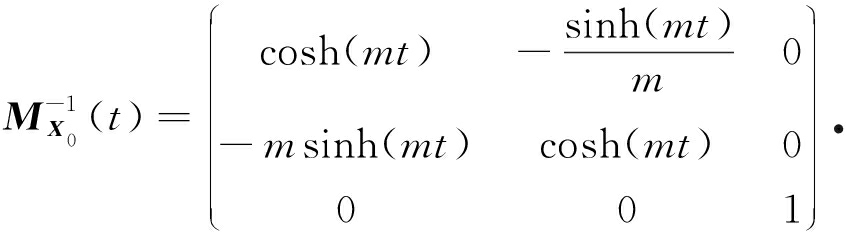
计算定理1中积分可得
(f1(X0), f2(X0), f3(X0)),
其中
求解非线性方程F(X0)=0,只能得到下面一个解:
S0=(0,0,0),
故系统(1)在原点处发生zero-Hopf分岔时,没有产生周期解.
2 Double-zero分岔
本节将研究系统(1)double-zero平衡点的动力学行为,基于文献[12]中定理7.2和7.3,我们得知:
引理1[12] 假设原点是系统
的孤立奇点,故原系统可写成
其中φ(u),φ(u),ψ(u,v)是解析函数,φ(0)=φ(0)=0,r≥2,αr ≠0,βn可为零,当βn≠0时,n≥1.则奇点O的性态如下:
1) 当r=2m+1时,令![]() 那么下列表达成立:
那么下列表达成立:
(a) 如果αr>0,那么奇点O是鞍点;
(b) 如果αr<0,βn≠0,n是偶数,当n<m,或n=m且Δr≥0,那么奇点O是结点;
(c) 如果αr<0,βn≠0,n是奇数,当n<m,或n=m且Δr≥0,那么奇点O的邻域由一个双曲扇形和一个椭圆扇形组成;
(d) 如果αr<0,当βn=0,或βn≠0,n>m,Δr< 0,或βn≠0,n=m,Δr< 0,那么奇点O是中心或焦点.
2) 当r=2m时,那么下列表达成立:
(a) 如果βn=0,或βn≠0,n≥m,那么奇点O是退化奇点;
(b) 如果βn≠0, n<m,那么奇点O是鞍结点.
基于引理1,系统(1)在原点处的double-zero局部动力学行为由如下定理给出.
定理3 当参数值经过临界值b=0,ρr=-1时,系统(1)在原点平衡点处会发生double-zero分岔,且有以下4种情况:
1) 当b>0,ρr>-1时,平衡点E0是鞍点,且有一维稳定流形和二维不稳定流形;
2) 当b>0,ρr<-1时,平衡点E0是中心或焦点,且有三维稳定流形;
3) 当b<0,ρr<-1时,平衡点E0是鞍点,且有三维不稳定流形;
4) 当b<0,ρr>-1时,平衡点E0是中心或焦点,且有一维不稳定流形和二维稳定流形.
证明 令a=-1-ρr,d=0,系统(1)转换为如下系统:

其在原点平衡点处的Jacobi矩阵为

矩阵A1的特征值为
λ1=0, λ2=0, λ3=-b,
对应的特征向量为
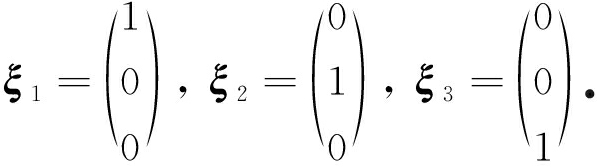
运用中心流形定理,将三维流形限制在特征值为零所对应的中心流形上,平衡点E0在λ1=0,λ2=0附近的稳定性由αr,βn的符号,n,m的大小及r的奇偶性决定.通过计算,可以得到中心流形为
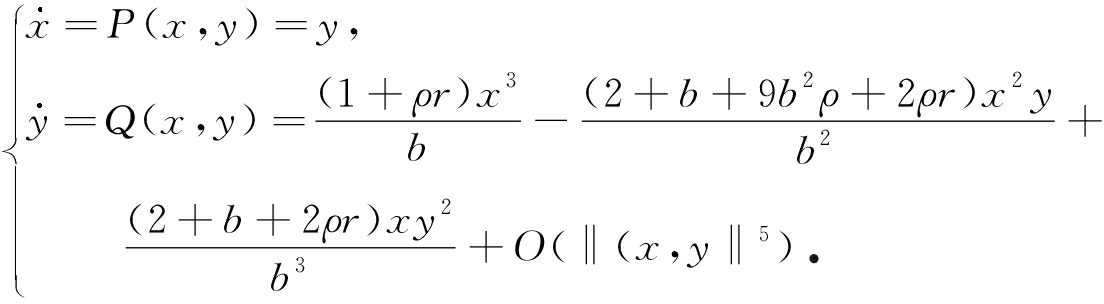
根据上式,可以得到
Q(x,y)=α3x3(1+ φ(x))+β2x2y(1+φ(x))+y2ψ(x,y),
其中,φ(x),φ(x),ψ(x,y)是解析函数,α3=(1+ρr)/b,β2=-(2+b+9b2ρ+2ρr)/b2,通过讨论α3和β2的符号即可得到定理3.
3 无穷远处的动力学行为
这一节将研究系统(1)的流在其无穷远处的动力学行为,为方便研究,我们将系统(1)重写为
其中
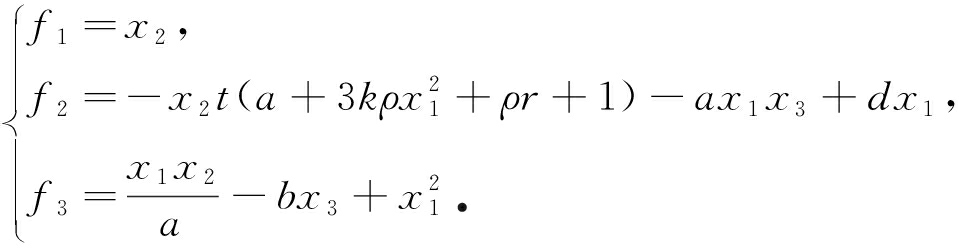
(8)
根据R3空间中的Poincaré紧致化方法[13],通过可逆的坐标变换,将原系统(1)在其相空间R3中的向量场投影到坐标卡Ui,Vi(i=1,2,3)上,然后分析坐标卡上的新向量场即可.下面分别在坐标卡Ui,Vi(i=1,2,3)上研究系统(1)的动力学行为[14].
3.1 局部坐标卡U1及V1
系统(1)在局部坐标卡U1下的Poincaré紧致化的表达式为

(9)
空间{(z1,z2,z3)∈R3|z3=0}在系统(9)的作用下保持不变,其对应于系统(8)相空间R3的无穷远处.系统(9)具有一个二维平衡点平面,整个z1-z2平面上的点![]() 都是系统(9)的平衡点,并且系统(9)在这些平衡点处的Jacobi矩阵的三个特征值全为零.
都是系统(9)的平衡点,并且系统(9)在这些平衡点处的Jacobi矩阵的三个特征值全为零.
为了完全描述系统(8)在无穷远球面上的动力学性质,限制在空间{(z1,z2,z3)∈R3|z3=0}上,系统(9)被约化为
(10)
当t=0时,令初始条件(z1,z2)=(z1(0),z2(0)),可得系统(10)具有如下形式的解:
z1=z1(0), z2=z2(0).
由于在坐标卡V1上的紧致化向量场与坐标卡U1上的紧致化向量场只差一个符号(-1),即系统(8)在局部坐标卡V1上的流与在局部坐标卡U1上的流相反.
3.2 局部坐标卡U2及V2
系统(1)在局部坐标卡U2下的Poincaré紧致化的表达式为

(11)
空间{(z1,z2,z3)∈R3|z3=0}在系统(11)的作用下保持不变,其对应于系统(8)相空间R3的无穷远处.系统(11)具有一个一维平衡点直线,z2轴上的点![]() 都是系统(11)的平衡点,并且系统(11)在这些平衡点处的Jacobi矩阵的三个特征值全为零.
都是系统(11)的平衡点,并且系统(11)在这些平衡点处的Jacobi矩阵的三个特征值全为零.
为了完全描述系统(8)在无穷远球面上的动力学性质,限制在空间{(z1,z2,z3)∈R3|z3=0}上,系统(11)被约化为
(12)
系统(12)与系统(10)是完全一样的.
系统(8)在局部坐标卡V2上的流也与在局部坐标卡U2上的流相反.
3.3 局部坐标卡U3及V3
系统(1)在局部坐标卡U3下的Poincaré紧致化的表达式为
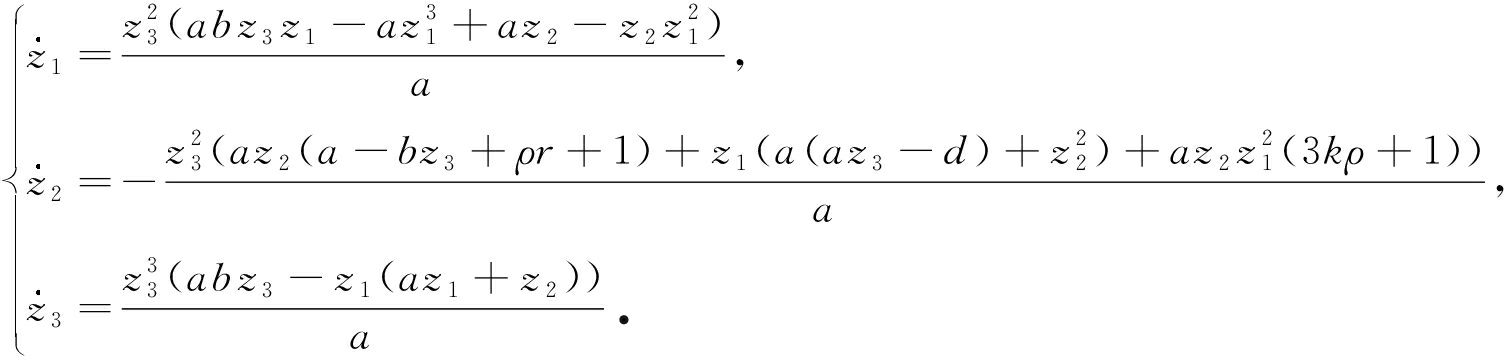
(13)
当z3=0时,与坐标卡U2的情形类似,原点(0,0,0)为系统(13)的平衡点,并且在该平衡点处,系统(13)的Jacobi矩阵的三个特征值全为零.
限制在空间{(z1,z2,z3)∈R3|z3=0}上,系统(13)被约化为
(14)
系统(14)与系统(12)也是完全一样的.
系统(8)在局部坐标卡V3上的流也与在局部坐标卡U3上的流相反.
定理4 对任意实参数a,b,d,ρ,r,k,系统(1)在无穷远处具有如下动力学性质:
1) 系统(1)的所有无穷远奇点都落在空间{(x,y,z)∈R3|x≠0}的无穷远处,反之也成立,即,空间{(x,y,z)∈R3|x≠0}无穷远处的所有点都是系统(1)的无穷远奇点;
2) 限制在空间{(x,y,z)∈R3|x=0,y≠0}无穷远处,系统(1)与系统(12)拓扑共轭;
3) 限制在空间{(x,y,z)∈R3|x=0,y=0,z≠0}无穷远处,系统(1)与系统(14)拓扑共轭.
4 结 论
本文研究了一类具有忆阻器的Lorenz型系统的余维二分岔及无穷远处动力学行为问题,利用平均理论得到了系统发生zero-Hopf分岔的条件以及分岔情况,在中心流形定理的基础上给出了系统发生double-zero分岔时的稳定性分析,最后根据Poincaré映射在四维空间的三组坐标卡上分析了系统的无穷远处的动力学行为.关于无穷远处动力学的研究,弥补了系统局部分析的不足,丰富了系统全局动力学行为.通过以上研究,表明忆阻器混沌系统的高余维分岔与余维一分岔差异巨大,丰富了我们对忆阻器混沌系统高余维分岔特性的认识.在以后的研究中,高余维分岔或将成为分析忆阻器混沌系统中必不可少的一环.
参考文献(References):
[1] BAO B C, XU J P, LIU Z. Initial state dependent dynamical behaviors in a memristor based chaotic circuit[J]. Chinese Physics Letters, 2010, 27(7): 070504.
[2] LIN Z H, WANG H X. Efficient image encryption using a chaos-based PWL memristor[J]. IETE Technical Review, 2010, 27(4): 318-325.
[3] SUN J W, SHEN Y, YIN Q, et al. Compound synchronization of four memristor chaotic oscillator systems and secure communication[J]. Chaos, 2013, 23(1): 013140.
[4] 王伟, 曾以成, 陈争, 等. 忆阻器混沌电路产生的共存吸引子与Hopf分岔[J]. 计算物理, 2017, 34(6): 747-756.(WANG Wei, ZENG Yicheng, CHEN Zheng, et al. Coexisting attractors and Hopf bifuracation in floating memristors based chaotic ciruit[J]. Chinese Journal of Computtaional Physics, 2017, 34(6): 747-756.(in Chinese))
[5] 陈秋杰, 李文. 忆阻器混沌电路的硬件实现[J]. 工业控制计算机, 2018, 31(11): 155-156.(CHEN Qiujie, LI Wen. Hardware implementation of memristor chaotic circuit[J]. Industrial Control Computer, 2018, 31(11): 155-156.(in Chinese))
[6] 周鹍. 余维2的叉形分岔[J]. 力学与实践, 1996, 18(1): 26-27.(ZHOU Kun. The fork bifurcation of codimension 2[J]. Mechanics in Engineering, 1996, 18(1): 26-27.(in Chinese))
[7] 黄俊, 陈玉明. 一类具有忆阻器的Lorenz 型混沌系统稳定性及余维一分岔分析[J]. 应用数学进展, 2019, 8(4): 858-867.(HUANG Jun, CHEN Yuming. Stability and co-dimension one bifurcation analysis of a class of Lorenz chaotic systems with memristor[J]. Advances in Applied Mathematics, 2019, 8(4): 858-867.(in Chinese))
[8] 张海龙, 闵富红, 王恩荣. 关于Lyapunov指数计算方法的比较[J]. 南京师范大学学报(工程技术版), 2012, 12(1): 5-9.(ZHANG Hailong, MIN Fuhong, WANG Enrong. The comparison for Lyapunov exponents calculation methods[J]. Journal of Nanjing Normal University(Engineering and Technology Edition), 2012, 12(1): 5-9.(in Chinese))
[9] GUCKENHEIMER J. On a codimension two bifurcation[J]. Lecture Notes in Mathematics, 1981, 898: 99-142.
[10] 韩茂安. 三维系统余维二分支中周期轨道与不变环面的存在性[J]. 系统科学与数学, 1998, 18(4): 403-409.(HAN Maoan. Existence of periodic orbits and invariant tori in co-dimension two bifurcations of three dimensional systems[J]. Journal of Systems Science and Mathematical Sciences, 1998, 18(4): 403-409.(in Chinese))
[11] CHEN Y M, LIANG H H. Zero-zero-Hopf bifurcation and ultimate bound estimation of a generalized Lorenz-Stenflo hyperchaotic system[J]. Mathematical Methods in the Applied Sciences, 2017, 40: 3424-3432.
[12] 张芷芬, 丁同仁, 黄文灶, 等. 微分方程定性理论[M]. 北京: 科学出版社, 1997.(ZHANG Zhifen, DING Tongren, HUANG Wenzao, et al. Qualitative Theory of Differential Equations[M]. Beijing: Science Press, 1997.(in Chinese))
[13] CIMA A, LLIBRE J. Bounede polynomial vector fields[J]. Transactions of the American Mathematical Society, 1990, 318: 557-579.
[14] 陈玉明. 基于Lorenz型系统的四维超混沌系统的复杂动力学研究[D]. 博士学位论文. 广州: 华南理工大学, 2014.(CHEN Yuming. Research on complex dynamics of four-dimensional hyperchaotic systems based on Lorenz-type systems[D]. PhD Thesis. Guangzhou: South China University of Technology, 2014.(in Chinese))