引 言
标量化是求解向量优化问题一种重要和有效的方法.按照使用的函数不同,标量化可分为线性标量化和非线性标量化.线性标量化的优势在于简单易行,因而取得了丰硕的成果[1-4],但受限于对向量优化问题的目标函数及可行集要具备一定的凸性或广义凸性条件.为此在更一般的非凸情形下,非线性标量化方法日益受到重视并被广泛地应用,其中最为著名的非线性标量化函数之一就是Gerstewitz泛函[5-6].Gerstewitz泛函的许多重要性质,特别是非凸分离性质[7-9],已经被成功地应用到处理向量优化领域中的各种问题[10-14].
对可变序结构下向量优化理论的研究已日益受到学者们的关注和重视.向量优化理论中的可变序结构及其相关非控解的概念最早是由Yu[15]提出来的.在那之后,可变序结构下的向量优化理论逐渐得到了丰富与发展[16].其中众多结果都是通过可变序结构下的非线性标量化函数得以实现的.Chen等[17]通过推广固定序结构下的非线性标量化函数Gerstewitz泛函的形式,在赋范线性空间中首次引入了可变序结构下非线性标量化函数的概念.作为应用,文献[17]中建立了向量优化问题和向量变分不等式问题的弱非控解的标量化定理.后来,在Hausdorff局部凸空间中,Chen等[18]又给出了可变序结构下非线性标量化函数更为一般的定义,并利用该函数建立了广义拟向量平衡问题的解的存在性结果.文献[17-18]均指出可变序结构下非线性标量化函数拥有同固定序结构下非线性标量化函数共同的性质,包括次线性性与连续性.文献[18]还讨论了可变序结构下非线性标量化函数作为二元函数的上、下半连续性.Farajzadeh等[19]在文献[18]的基础上进一步减弱了对空间的假设要求.在一般的拓扑向量空间中,在更弱的假设条件下,文献[19]建立了可变序结构下非线性标量化函数的上、下半连续性.邵重阳等[20]运用可变序结构下的非线性标量化函数得到了一类参数广义弱向量拟平衡问题解映射H-连续的充要条件.另一方面,对应于固定序结构下的Gerstewitz泛函,Luc等[21]给出了另一个称为最大严格单调函数的非线性标量化函数的定义形式.
本文的主要工作是给出文献[21]中的非线性标量化函数在可变序结构下的对应形式并分析其相应性质.在此基础上定义了一个新的非线性函数并证明其是一个半范数.同时在文献[18-19]的假设条件之下讨论了以上两个函数的上、下半连续性.本文所建立的结果是对文献[18-19]中相应结论的扩展和延伸.
说明一下文中要使用的概念和符号.设Y是一个拓扑向量空间,Y*是Y的拓扑对偶空间.设K⊂Y为真凸锥,即K+K⊂K,λK⊂K,∀λ∈R+且K≠Y.若K∩(-K)={0},则称K是点锥.设S⊂Y,则int S,cl S和bd S分别表示S的内部、闭包和边界.S的对偶锥为S*={φ∈Y*: φ(y)≥0,∀y∈S}.此外,Lim{yn}表示序列{yn}⊂Y的所有极限点构成的集合.
按通常记法,设K⊂Y为内部非空的真闭凸锥,则空间Y中的偏序定义如下: 对任何的y, z∈Y,y≤Kz ⟺ z-y∈K;y<Kz ⟺ z-y∈int K.令R=(-∞,+∞), 且R+=[0,+∞).给定向量y∈Y, 则集合Ry![]() {ry: r∈R}.
{ry: r∈R}.
设X是向量空间,且F:X![]() Y是一个集值映射.若对任何x∈X,F(x)是Y中的闭集,则称F是一个闭值映射.若F的图像Graph F={(x,y)∈X×Y: y∈F(x)}是闭的,则称F是一个闭映射.称F在点x0∈X处是上半连续的,如果对F(x0)的任何邻域U,都存在x0的邻域V,使得F(x)⊂U,∀x∈V.称F在X上是上半连续的,如果F在任何点x0∈X处是上半连续的.
Y是一个集值映射.若对任何x∈X,F(x)是Y中的闭集,则称F是一个闭值映射.若F的图像Graph F={(x,y)∈X×Y: y∈F(x)}是闭的,则称F是一个闭映射.称F在点x0∈X处是上半连续的,如果对F(x0)的任何邻域U,都存在x0的邻域V,使得F(x)⊂U,∀x∈V.称F在X上是上半连续的,如果F在任何点x0∈X处是上半连续的.
1 非线性标量化函数
设Y是一个Hausdorff拓扑向量空间,K:Y![]() Y是一个集值映射,满足对任何的x∈Y,K(x)是Y中的一个内部int K(x)非空的真闭凸锥.e:Y→Y是一个映射,满足e(x)∈int K(x),∀x∈Y.首先,回顾一下可变序结构下非线性标量化函数Gerstewitz泛函的定义[9,18].
Y是一个集值映射,满足对任何的x∈Y,K(x)是Y中的一个内部int K(x)非空的真闭凸锥.e:Y→Y是一个映射,满足e(x)∈int K(x),∀x∈Y.首先,回顾一下可变序结构下非线性标量化函数Gerstewitz泛函的定义[9,18].
定义1 函数ξ:Y×Y→R定义为
ξ(x,y)=inf{t∈R: y∈te(x)-K(x)}, x,y∈Y.
(1)
下面的命题集中给出了ξ(·,·)的性质[9,18].
命题1 设x,y,z∈Y,λ∈R:
 ξ(x,y)<λ⟺y∈λe(x)-int K(x),ξ(x,y)≥λ⟺y∉λe(x)-int K(x);
ξ(x,y)<λ⟺y∈λe(x)-int K(x),ξ(x,y)≥λ⟺y∉λe(x)-int K(x);
 ξ(x,y)≤λ⟺y∈λe(x)-K(x),ξ(x,y)>λ⟺y∉λe(x)-K(x);
ξ(x,y)≤λ⟺y∈λe(x)-K(x),ξ(x,y)>λ⟺y∉λe(x)-K(x);
 ξ(x,y)=λ⟺y∈λe(x)-bd K(x);
ξ(x,y)=λ⟺y∈λe(x)-bd K(x);
 ξ(x,y+λe)=ξ(x,y)+λ;
ξ(x,y+λe)=ξ(x,y)+λ;
 若y≤K(x)z,则ξ(x,y)≤ξ(x,z),若y<K(x)z,则ξ(x,y)<ξ(x,z);
若y≤K(x)z,则ξ(x,y)≤ξ(x,z),若y<K(x)z,则ξ(x,y)<ξ(x,z);
 ξ(x,·)是正齐次的,即ξ(x,λy)=λξ(x,y),λ∈R+;
ξ(x,·)是正齐次的,即ξ(x,λy)=λξ(x,y),λ∈R+;
 ξ(x,·)是次可加的,即ξ(x,y+z)≤ξ(x,y)+ξ(x,z);
ξ(x,·)是次可加的,即ξ(x,y+z)≤ξ(x,y)+ξ(x,z);
 ξ(x,·)是连续的.
ξ(x,·)是连续的.
对应于Gerstewitz泛函,下面是另一种非线性标量化函数最大严格单调函数η:Y→R的定义形式[21].设K是Y中的一个真闭凸锥,且e∈int K,则
η(y)=sup{t∈R: y∈te+K}, y∈Y.
(2)
现在,我们可以给出该非线性标量化函数在可变序结构下的对应形式.
定义2 非线性标量化函数η:Y×Y→R定义为
η(x,y)=sup{t∈R: y∈te(x)+K(x)}, x,y∈Y.
(3)
注1 设K是Y中的一个真闭凸锥,且e∈int K.若对任何的x∈Y,令K(x)=K,e(x)=e,则上述定义中的函数η(·,·)就退化为其固定序结构下的常见形式.
下面的引理表明函数η(·,·)的定义是合理的.
引理1 设x,y∈Y,令Γ(x,y)![]() {t∈R: y∈te(x)+K(x)},则有
{t∈R: y∈te(x)+K(x)},则有
 Γ(x,y)是非空闭集;
Γ(x,y)是非空闭集;
 若t∈Γ(x,y)且r<t,则r∈Γ(x,y);
若t∈Γ(x,y)且r<t,则r∈Γ(x,y);
 Γ(x,y)是上有界的.
Γ(x,y)是上有界的.
证明  对y∈Y,由e(x)∈int K(x)可知, ∃λ>0使得e(x)+λy∈K(x).于是y∈
对y∈Y,由e(x)∈int K(x)可知, ∃λ>0使得e(x)+λy∈K(x).于是y∈
(-1/λ)e(x)+K(x),即-1/λ∈Γ(x,y).从而Γ(x,y)≠∅.假设{tn}⊂Γ(x,y)且tn→t0,则y∈tne(x)+K(x).即y-tne(x)∈K(x).令n→+∞且注意到K(x)是闭集,可得y-t0e(x)∈K(x),即y∈t0e(x)+K(x).这表明Γ(x,y)是闭集.
 假设t∈Γ(x,y),r<t,则
假设t∈Γ(x,y),r<t,则
y∈te(x)+K(x)=re(x)+K(x)+(t-r)e(x)⊆
re(x)+K(x)+int K(x)⊆re(x)+K(x).
因此 r∈Γ(x,y).
 反证.假设Γ(x,y)不是上有界的.根据
反证.假设Γ(x,y)不是上有界的.根据 ,可知Γ(x,y)=R.这样就有y∈te(x)+K(x),∀t∈R.设k∈K(x),λ∈R.由于K(x)是凸集,则对任何的n∈N,((n-1)/n)k+(1/n)(y+nλe(x))∈K(x).令n→+∞,考虑到K(x)是闭集,得到k+λe(x)∈K(x).于是K(x)+Re(x)⊆K(x).结合
,可知Γ(x,y)=R.这样就有y∈te(x)+K(x),∀t∈R.设k∈K(x),λ∈R.由于K(x)是凸集,则对任何的n∈N,((n-1)/n)k+(1/n)(y+nλe(x))∈K(x).令n→+∞,考虑到K(x)是闭集,得到k+λe(x)∈K(x).于是K(x)+Re(x)⊆K(x).结合 中的证明不难知道,Y=Re(x)+K(x)⊆K(x).这与K(x)是真的相矛盾.证毕.
中的证明不难知道,Y=Re(x)+K(x)⊆K(x).这与K(x)是真的相矛盾.证毕.
从引理1得知,函数η(·,·)是一个定义良好的函数且定义中的上确界是可以取到的.因此,对任何的x,y∈Y,可得y∈η(x,y)e(x)+K(x).
同命题1类似,可将固定序结构下函数η(·)的性质推广到函数η(·,·).
命题2 设x,y,z∈Y,λ∈R:
 η(x,y)>λ⟺y∈λe(x)+int K(x),η(x,y)≤λ⟺y∉λe(x)+int K(x);
η(x,y)>λ⟺y∈λe(x)+int K(x),η(x,y)≤λ⟺y∉λe(x)+int K(x);
 η(x,y)≥λ⟺y∈λe(x)+K(x),η(x,y)<λ⟺y∉λe(x)+K(x);
η(x,y)≥λ⟺y∈λe(x)+K(x),η(x,y)<λ⟺y∉λe(x)+K(x);
 η(x,y)=λ⟺y∈λe(x)+bd K(x);
η(x,y)=λ⟺y∈λe(x)+bd K(x);
 η(x,y+λe)=η(x,y)+λ;
η(x,y+λe)=η(x,y)+λ;
 若y≤K(x)z,则η(x,y)≤η(x,z),若y<K(x)z,则η(x,y)<η(x,z);
若y≤K(x)z,则η(x,y)≤η(x,z),若y<K(x)z,则η(x,y)<η(x,z);
 η(x,·)是正齐次的,即η(x,λy)=λη(x,y),λ∈R+;
η(x,·)是正齐次的,即η(x,λy)=λη(x,y),λ∈R+;
 η(x,·)是超可加的,即η(x,y+z)≥η(x,y)+η(x,z);
η(x,·)是超可加的,即η(x,y+z)≥η(x,y)+η(x,z);
 η(x,·)是连续的.
η(x,·)是连续的.
结合上面的两个命题可得,在可变序结构之下,两个非线性标量化函数ξ(·,·)和η(·,·)一方面拥有各自不同的非凸分离性质,另一方面还拥有共同的性质:平移性、单调性、正齐次性和连续性.与此同时,下面的命题进一步提供了二者的更多信息和相互关系,这在后面的分析中起到了关键作用.
命题3 设x,y∈Y,则下面的结论成立:
 ξ(x,-y)=-η(x,y),η(x,-y)=-ξ(x,y);
ξ(x,-y)=-η(x,y),η(x,-y)=-ξ(x,y);
 ξ(x,y)=inf{t∈R:y∈te(x)-int K(x)};
ξ(x,y)=inf{t∈R:y∈te(x)-int K(x)};
 η(x,y)=sup{t∈R:y∈te(x)+int K(x)};
η(x,y)=sup{t∈R:y∈te(x)+int K(x)};
 假设K(x)是点锥,∀x∈Y,则ξ(x,y)≥η(x,y),且ξ(x,y)=η(x,y)⟺y∈Re(x);
假设K(x)是点锥,∀x∈Y,则ξ(x,y)≥η(x,y),且ξ(x,y)=η(x,y)⟺y∈Re(x);
 假设{yn}⊆Y,若ξ(x,yn)→0,则Lim{yn}⊆-bd K(x);若η(x,yn)→0,则Lim{yn}⊆bd K(x).
假设{yn}⊆Y,若ξ(x,yn)→0,则Lim{yn}⊆-bd K(x);若η(x,yn)→0,则Lim{yn}⊆bd K(x).
证明  直接利用上下确界的关系可得.
直接利用上下确界的关系可得.
 与
与 的证明过程类似,故略去.
的证明过程类似,故略去.
 令θ(x,y)
令θ(x,y)![]() sup{t∈R: y∈te(x)+int K(x)},则明显地η(x,y)≥θ(x,y).对每一个满足y∈te(x)+K(x)的实数t而言,分两种情形讨论:
sup{t∈R: y∈te(x)+int K(x)},则明显地η(x,y)≥θ(x,y).对每一个满足y∈te(x)+K(x)的实数t而言,分两种情形讨论:
(a) y∈te(x)+int K(x),于是t≤θ(x,y).
(b) y∈te(x)+bd K(x),即y-te(x)∈bd K(x).因K(x)是闭凸集且e(x)∈int K(x),故有
λ(y-te(x))+(1-λ)e(x)∈int K(x), ∀λ∈(0,1).
这等价于
根据θ(x,y)的定义,可得
令λ→1,就有t≤θ(x,y).
综合(a)、(b)并且利用t的任意性知,η(x,y)≤θ(x,y).从而η(x,y)=θ(x,y).
 反证.假设不然,∃x,y∈Y使得ξ(x,y)<η(x,y).根据命题1
反证.假设不然,∃x,y∈Y使得ξ(x,y)<η(x,y).根据命题1 和命题2
和命题2 有
有
y∈η(x,y)e(x)-int K(x), y∈η(x,y)e(x)+K(x).
这样推出y-η(x,y)e(x)∈(-int K(x))∩K(x).这与K(x)是点锥因而(-int K(x))∩K(x)=∅的事实相矛盾.故ξ(x,y)≥η(x,y),∀x,y∈Y.注意到ξ(x,0)=η(x,0)=0.在命题1 和命题2
和命题2 中令y=0,得到
中令y=0,得到
y∈Re(x)⟹ξ(x,y)=η(x,y).
另一方面,若ξ(x,y)=η(x,y),由于
y∈ξ(x,y)e(x)-K(x), y∈η(x,y)e(x)+K(x),
可得
y-ξ(x,y)e(x)=y-η(x,y)e(x)∈(-K(x))∩K(x).
而K(x)是点的,故y-ξ(x,y)e(x)=y-η(x,y)e(x)=0,这表明y∈Re(x).
 假设ξ(x,yn)→0.若Lim{yn}
假设ξ(x,yn)→0.若Lim{yn} -bd K(x),则一定存在y∈Y,ynk→y,使得y∉ -bd K(x).因此,根据函数ξ(x,·)的连续性可知,ξ(x,ynk)→ξ(x,y).故ξ(x,y)=0.根据命题1
-bd K(x),则一定存在y∈Y,ynk→y,使得y∉ -bd K(x).因此,根据函数ξ(x,·)的连续性可知,ξ(x,ynk)→ξ(x,y).故ξ(x,y)=0.根据命题1 得,y∈-bd K(x).矛盾! 函数η(·,·)的情形类似,省略.证毕.
得,y∈-bd K(x).矛盾! 函数η(·,·)的情形类似,省略.证毕.
下面的命题指出了在对偶空间情形下函数η(·,·)的具体表现形式.
命题4 设Ω:Y![]() Y*\{0}是一个集值映射,且对任何的x∈Y,K(x)={y∈Y: φ(y)≥0,∀φ∈Ω(x)}.则
Y*\{0}是一个集值映射,且对任何的x∈Y,K(x)={y∈Y: φ(y)≥0,∀φ∈Ω(x)}.则
(4)
证明 首先,我们指出φ(e(x))>0,∀φ∈Ω(x).若不然,存在φ0∈Ω(x)满足φ0(e(x))≤0.因e(x)∈int K(x),φ0(e(x))≥0,则φ0(e(x))=0.而φ0≠0且是线性的,一定存在y0∈Y使得φ0(y0)<0.又e(x)∈int K(x),可以找到α>0满足e(x)+αy0∈K(x).于是利用K(x)的定义,就有0≤φ0(e(x)+αy0)=φ0(e(x))+αφ0( y0)=αφ0( y0)<0.矛盾!
一方面,因为y∈η(x,y)e(x)+K(x),φ(y-η(x,y)e(x))≥0,∀φ∈Ω(x).即φ(y)-η(x,y)φ(e(x))≥0,∀φ∈Ω(x).而φ(e(x))>0,可得
于是
另一方面,令
ρ(x,y)![]()
![]()
显然有
这就蕴含φ(y-ρ(x,y)e(x))≥0,∀φ∈Ω(x).再次使用K(x)的定义,得到y-ρ(x,y)e(x)∈K(x).即y∈ρ(x,y)e(x)+K(x).根据η(x,y)的定义知,ρ(x,y)≤η(x,y),从而η(x,y)=ρ(x,y).证毕.
推论1 设Y是局部凸空间,则
(5)
其中K*(x)为K(x)的对偶锥.若B*(x)是K*(x)的一个基,则
(6)
证明 给定x∈Y.由于K(x)是局部凸空间Y中的闭凸锥,根据文献[10]中的引理3.21(a),可知K(x)={y∈Y:φ(y)≥0,∀φ∈K*(x)}.用K*(x)\{0}取代命题4中的Ω(x),得到式(5)成立.若B*(x)是K*(x)的一个基,则对每一个φ∈K*(x)\{0},存在λ>0,φ∈B*(x),使得φ=λφ.这样就有
两端同时取上确界且仍用φ来表示,可得式(6)成立.证毕.
推论2 设Y是一个局部凸空间,则η(x,y)=minφ∈B*(x)e(x)φ(y),其中B*(x)e(x)={φ∈K*(x):φ(e(x))=1}.
证明 利用文献[8]中的引理2.2.17,可得B*(x)e(x)={φ∈K*(x):φ(e(x))=1}是K*(x)的一个弱*紧基.将式(5)中的B*(x)用B*(x)e(x)代替并注意到φ∈B*(x)e(x)时φ(e(x))=1,就有η(x,y)=infφ∈B*(x)e(x)φ(y).而B*(x)e(x)是弱*紧基,于是结论成立.证毕.
2 半范数族和一类赋范线性空间
本节中假设Y是Hausdorff拓扑向量空间,集值映射K:Y![]() Y满足条件: ∀x∈Y,K(x)是一个真闭凸点锥,且int K(x)≠∅.向量值映射e:Y→Y满足条件:∀x∈Y,e(x)∈int K(x).在有了之前的准备后,现在我们通过函数ξ(·,·)和η(·,·)定义一个特别的函数.
Y满足条件: ∀x∈Y,K(x)是一个真闭凸点锥,且int K(x)≠∅.向量值映射e:Y→Y满足条件:∀x∈Y,e(x)∈int K(x).在有了之前的准备后,现在我们通过函数ξ(·,·)和η(·,·)定义一个特别的函数.
定义3 函数p:Y×Y→R定义为
p(x,y)![]() ξ(x,y)-η(x,y), ∀x,y∈Y.
ξ(x,y)-η(x,y), ∀x,y∈Y.
(7)
利用命题1~3,我们可以得到函数p(·,·)很多好的性质.
命题5 设x,y,z∈Y,λ∈R:
 p(x,y)≥0,且p(x,y)=0 ⟺ y∈Re(x);
p(x,y)≥0,且p(x,y)=0 ⟺ y∈Re(x);
 p(x,λy)=|λ|p(x,y);
p(x,λy)=|λ|p(x,y);
 p(x,y+z)≤p(x,y)+p(x,z);
p(x,y+z)≤p(x,y)+p(x,z);
 p(x,·)是连续的.
p(x,·)是连续的.
证明  根据命题3
根据命题3 及函数p(·,·)的定义直接可得.
及函数p(·,·)的定义直接可得.
 若λ≥0,则结论成立,这是由于函数ξ(x,·)和η(x,·)均是正齐次的,∀x∈Y.下设λ<0.根据命题3
若λ≥0,则结论成立,这是由于函数ξ(x,·)和η(x,·)均是正齐次的,∀x∈Y.下设λ<0.根据命题3 、命题1
、命题1 及命题2
及命题2 ,有
,有
p(x,λy)=ξ(x,λy)-η(x,λy)=
-η(x,-λy)+ξ(x,-λy)=
λη(x,y)-λξ(x,y)=-λp(x,y).
 根据命题1
根据命题1 和命题2
和命题2 知,函数ξ(x,·)和-η(x,·)均是次可加的,即
知,函数ξ(x,·)和-η(x,·)均是次可加的,即
ξ(x,y+z)≤ξ(x,y)+ξ(x,z),-η(x,y+z)≤-η(x,y)-η(x,z).
上面两个不等式相加可得p(x,y+z)≤p(x,y)+p(x,z).
 利用函数ξ(x,·)和η(x,·)的连续性,结论直接可得.证毕.
利用函数ξ(x,·)和η(x,·)的连续性,结论直接可得.证毕.
定理1 对任何的x∈Y,函数p(x,·)是空间Y上一个连续的半范数.
证明 根据命题5,函数p(x,·)是非负、正齐次、次可加且对称的.因而它是Y上的一个半范数.证毕.
因此,若τ表示空间Y上的由半范数族{p(x,·): x∈Y}生成的拓扑,则(Y,τ)就是一个局部凸空间.然而,p(x,y)=0对于整条直线Re(x)上的所有点y均成立,故p(x,·)不是Y上的范数.即(Y,τ)不是赋范线性空间.
尽管如此,仍然有一个合适的方法构造出一类赋范线性空间.在这之前,需要定义一个空间Y上的等价关系.为此,对x∈Y,可令: y~z ⟺ y-z∈Re(x).于是对任何的y,z,w∈Y,容易验证: (a) y~y; (b) y~z ⟺ z~y;(c) y~z,z~w ⟹ y~w.这表明,关系~的确是一个等价关系.设[y]表示以y为代表的等价类,Γx表示Y中所有等价类构成的集合,即Γx={[y]:y∈Y}.
定理2 对任何的x∈Y,函数‖·‖x:Γx→R定义为
‖[y]‖x=p(x,y), ∀[y]∈Γx,
(8)
则(Γx,‖·‖x)是一个赋范线性空间.
证明 首先,在Γx上定义线性运算,使其成为一个线性空间.设[y],[z]∈Γx,λ∈R,线性运算定义为: [y]+[z]
[y]+[z]![]() [y+z];
[y+z];  λ·[y]
λ·[y]![]() [λy].不难证明,Γx在上述运算下是一个线性空间.
[λy].不难证明,Γx在上述运算下是一个线性空间.
剩下只需证明函数‖·‖x是Γx上的一个范数.事实上,在Γx中,[0]=Re(x).根据命题5 ,‖[y]‖x=0 ⟺ [y]=[0].结合定理1,可得‖·‖x是一个范数.证毕.
,‖[y]‖x=0 ⟺ [y]=[0].结合定理1,可得‖·‖x是一个范数.证毕.
3 非线性标量化函数及半范数的半连续性
定理3 设Y是一个拓扑向量空间,且S⊂Y是一个闭子集.又K:S![]() Y是一个集值映射,满足对任何的x∈S,K(x)是一个内部非空的真闭凸锥.而e:S→Y是一个连续映射,使得e(x)∈int K(x),∀x∈S.若定义集值映射W:S
Y是一个集值映射,满足对任何的x∈S,K(x)是一个内部非空的真闭凸锥.而e:S→Y是一个连续映射,使得e(x)∈int K(x),∀x∈S.若定义集值映射W:S![]() Y为: W(x)=Y\int K(x),∀x∈S.则下面的结论成立:
Y为: W(x)=Y\int K(x),∀x∈S.则下面的结论成立:
 若映射K是闭的,则函数η(·,·)在S×S上是上半连续的;
若映射K是闭的,则函数η(·,·)在S×S上是上半连续的;
 若映射W是闭的,则函数η(·,·)在S×S上是下半连续的.
若映射W是闭的,则函数η(·,·)在S×S上是下半连续的.
证明  设λ∈R,只需证明集合
设λ∈R,只需证明集合
A(λ)={(x,y)∈S×S: η(x,y)≥λ}
是闭的.
事实上,设{(xα,yα)}α∈I是A(λ)中的网,且(xα,yα)→(x,y).由(xα,yα)∈A(λ),根据命题2 可得yα∈λe(xα)+K(xα).即yα-λe(xα)∈K(xα).又e(·)是连续的,则
可得yα∈λe(xα)+K(xα).即yα-λe(xα)∈K(xα).又e(·)是连续的,则
yα-λe(xα)→y-λe(x).
由已知集值映射K是闭映射,有y-λe(x)∈K(x).故y∈λe(x)+K(x).再使用命题2 ,可得η(x,y)≥λ.
,可得η(x,y)≥λ.
 设λ∈R,只需证明集合
设λ∈R,只需证明集合
B(λ)={(x,y)∈S×S: η(x,y)≤λ}
是闭集.
设{(xα,yα)}α∈I是B(λ)中的网,且(xα,yα)→(x,y).由(xα,yα)∈B(λ),根据命题2 可得yα∉ λe(xα)+int K(xα).即yα-λe(xα)∈Y\int K(xα)=W(xα).而e(·)是连续的,有yα-λe(xα)→y-λe(x).又已知集值映射W是闭映射,则y-λe(x)∈W(x).故y∉λe(x)+int K(x).再根据命题2
可得yα∉ λe(xα)+int K(xα).即yα-λe(xα)∈Y\int K(xα)=W(xα).而e(·)是连续的,有yα-λe(xα)→y-λe(x).又已知集值映射W是闭映射,则y-λe(x)∈W(x).故y∉λe(x)+int K(x).再根据命题2 ,得到η(x,y)≤λ.证毕.
,得到η(x,y)≤λ.证毕.
推论3 设Y是一个拓扑向量空间,集值映射K:Y![]() Y满足对任何的x∈Y,K(x)是一个真闭凸锥且int K(x)≠∅.映射e:Y→Y是集值映射int K(·)的一个连续选择.集值映射W:Y
Y满足对任何的x∈Y,K(x)是一个真闭凸锥且int K(x)≠∅.映射e:Y→Y是集值映射int K(·)的一个连续选择.集值映射W:Y![]() Y定义为: W(x)=Y\int K(x),∀x∈Y.则下面的结论成立:
Y定义为: W(x)=Y\int K(x),∀x∈Y.则下面的结论成立:
 若K是上半连续的,则η(·,·)在Y×Y上是上半连续的;
若K是上半连续的,则η(·,·)在Y×Y上是上半连续的;
 若W是上半连续的,则η(·,·)在Y×Y上是下半连续的.
若W是上半连续的,则η(·,·)在Y×Y上是下半连续的.
证明 由于集值映射K(W)是上半连续的并且是闭值的,故K(W)一定是闭映射.根据定理3,可得结论成立.证毕.
结合定理3与文献[19]中的定理2.2,可得定义3中的函数p(·,·)的半连续性质.
定理4 设Y是一个拓扑向量空间, 且S⊂Y是一个闭子集.又K: S![]() Y是一个集值映射, 满足对任何的x∈S, K(x)是一个内部非空的真闭凸点锥.其余假设同定理3.则下面的结论成立:
Y是一个集值映射, 满足对任何的x∈S, K(x)是一个内部非空的真闭凸点锥.其余假设同定理3.则下面的结论成立:
 若映射W是闭的,则函数p(·,·)在S×S上是上半连续的;
若映射W是闭的,则函数p(·,·)在S×S上是上半连续的;
 若映射K是闭的,则函数p(·,·)在S×S上是下半连续的.
若映射K是闭的,则函数p(·,·)在S×S上是下半连续的.
证明  由于W是闭映射,根据定理3,函数η(·,·)在S×S上是下半连续的.进一步根据文献[19]中的定理2.2,函数ξ(·,·)在S×S上是上半连续的.因此函数p(·,·)在S×S上是上半连续的.
由于W是闭映射,根据定理3,函数η(·,·)在S×S上是下半连续的.进一步根据文献[19]中的定理2.2,函数ξ(·,·)在S×S上是上半连续的.因此函数p(·,·)在S×S上是上半连续的.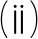 的证明类似.证毕.
的证明类似.证毕.
推论4 设Y是一个拓扑向量空间,集值映射K:Y![]() Y满足对任何的x∈Y,K(x)是一个真闭凸点锥且int K(x)≠∅.其余假设同推论3.则下面的结论成立:
Y满足对任何的x∈Y,K(x)是一个真闭凸点锥且int K(x)≠∅.其余假设同推论3.则下面的结论成立:
 若W是上半连续的,则p(·,·)在Y×Y上是上半连续的;
若W是上半连续的,则p(·,·)在Y×Y上是上半连续的;
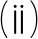 若K是上半连续的,则p(·,·)在Y×Y上是下半连续的.
若K是上半连续的,则p(·,·)在Y×Y上是下半连续的.
证明 集值映射W(K)是上半连续的闭值映射,因而一定是闭映射.根据定理4即得结论成立.证毕.
注2 从定理3的证明过程中可以看出,保证函数η(·,·)在S×S上上半连续的充分条件K是闭映射可进一步减弱为:对任何的λ∈R,集值映射x→λe(x)+K(x)是闭的.同样地,保证函数η(·,·)下半连续的充分条件W是闭映射可减弱为:对任何的λ∈R,集值映射x→λe(x)+W(x)是闭的.这与文献[19]中定理2.3的情形是一致的.
4 结 论
本文给出了向量优化中最大严格单调函数这一非线性标量化函数在可变序结构下的定义形式,并对其性质进行了详细分析.文中建立了可变序结构下两个非线性标量化函数之间的联系,同时作为应用构造出了一族半范数并诱导出了一类赋范线性空间,最后在合适的假设条件下给出了非线性标量化函数和半范数的上、下半连续性结论.本文所得的结果在诸如投资组合优化、选址问题、医学图像配准等领域中具备一定的应用前景.如何将可变序结构下非线性标量化函数的性质加以充分利用,将是今后进一步研究的课题.
[1] YANG X M, YANG X Q, CHEN G Y. Theorems of the alternative and optimization with set-valued maps[J]. Journal of Optimization Theory and Applications, 2000, 107(3): 627-640.
[2] YANG X M, LI D, WANG S Y. Near-subconvexlikeness in vector optimization with set-valued functions[J]. Journal of Optimization Theory and Applications, 2001, 110(2): 413-427.
[3] 吴海琴, 刘学文, 罗萍. 集值优化问题广义近似解的线性标量化[J]. 重庆师范大学学报(自然科学版), 2017, 34(4): 13-16.(WU Haiqin, LIU Xuewen, LUO Ping. Nonlinear scalarization theorems of generalized approximate solutions in set-valued optimization problems[J]. Journal of Chongqing Normal University(Natural Science), 2017, 34(4): 13-16.(in Chinese))
[4] 刘学文, 王婷, 汪定国. 向量优化中广义E-Benson真有效解的性质研究[J]. 重庆师范大学学报(自然科学版), 2018, 35(3): 17-20.(LIU Xuewen, WANG Ting, WANG Dingguo. Characterizations of generalized E-Benson proper efficient solutions in vector optimization[J]. Journal of Chongqing Normal University(Natural Science), 2018, 35(3): 17-20.(in Chinese))
[5] GERSTEWITZ C H, IWANOW E. Dualität für nichtkonvexe vektoroptimierungsprobleme[J]. Wissensch Zeitschr Tech, 1985, 31: 61-81.
[6] LUC D T. Theory of Vector Optimization[M]. Berlin: Springer, 1989.
[7] GERTH C, WEIDNER P. Nonconvex separation theorems and some applications in vector optimization[J]. Journal of Optimization Theory and Applications, 1990, 67(2): 297-320.
[8] GÖPFERT A, RIAHI H, TAMMER C, et al. Variational Methods in Partially Ordered Spaces[M]. New York: Springer, 2003.
[9] CHEN G Y, HUANG X X, YANG X Q. Vector Optimization-Set-Valued and Variational Analysis[M]. Berlin: Springer, 2005.
[10] JAHN J. Vector Optimization-Theory, Applications and Extensions[M]. 2nd ed. Berlin: Springer, 2011.
[11] 戎卫东, 杨新民. 向量优化及其若干进展[J]. 运筹学学报, 2014, 18(1): 9-38.(RONG Weidong, YANG Xinmin. Vector optimization and its developments[J]. Operations Research Transactions, 2014, 18(1): 9-38.(in Chinese))
[12] 李伟佳, 朱巧, 赵克全. Gerstewitz非线性标量化函数的性质及其在向量优化中的应用[J]. 重庆师范大学学报(自然科学版), 2017, 34(5): 1-5.(LI Weijia, ZHU Qiao, ZHAO Kequan. Properties of Gerstewitz nonlinear scalarization function and applications in vector optimization[J]. Journal of Chongqing Normal University(Natural Science), 2017, 34(5): 1-5.(in Chinese))
[13] 朱巧, 徐威娜, 赵克全. 向量优化中Gerstewitz非线性标量化函数的拟内部性质[J]. 重庆师范大学学报(自然科学版), 2018, 35(1): 11-14.(ZHU Qiao, XU Weina, ZHAO Kequan. Properties of Gerstewitz nonlinear scalarization function via quasi interiors in vector optimization[J]. Journal of Chongqing Normal University(Natural Science), 2018, 35(1): 11-14.(in Chinese))
[14] ZHAO K Q, ZHU Q, WANG D G. Nonconvex separation theorems via assumption B and applications in vector optimization[J]. Journal of Chongqing Normal University(Natural Science), 2018, 35(3): 1-8.
[15] YU P L. Multiple-Criteria Decision Making: Concepts, Techniques and Extensions[M]. New York: Plenum Press, 1985.
[16] EICHFELDER G. Variable Ordering Structures in Vector Optimization[M]. Berlin: Springer, 2014.
[17] CHEN G Y, YANG X Q. Characterizations of variable domination structures via nonlinear scalarization[J]. Journal of Optimization Theory and Applications, 2002, 112(1): 97-110.
[18] CHEN G Y, YANG X Q, YU H. A nonlinear scalarization function and generalized quasi-vector equilibrium problems[J]. Journal of Global Optimization, 2005, 32(4): 451-466.
[19] FARAJZADEH A, LEE B S, PLUBTEING S. On generalized quasi-vector equilibrium problems via scalarization method[J]. Journal of Optimization Theory and Applications, 2015, 168(2): 1-16.
[20] 邵重阳, 彭再云, 王泾晶, 等. 参数广义弱向量拟平衡问题解映射的H-连续性刻画[J]. 应用数学和力学, 2019, 40(4): 452-462.(SHAO Chongyang, PENG Zaiyun, WANG Jingjing, et al. Characterizations of H-continuity for solution mapping to parametric generalized weak vector quasi-equilibrium problems[J]. Applied Mathematics and Mechanics, 2019, 40(4): 452-462.(in Chinese))
[21] LUC D T, RA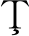 IU A. Vector optimization: basic concepts and solution methods[M]//AL-MEZEL S A R, AL-SOLAMY F R M, ANSARI Q H, ed. Fixed Point Theory, Variational Analysis and Optimization. Boca Raton: CRC Press, Taylor & Francis Group, 2014.
IU A. Vector optimization: basic concepts and solution methods[M]//AL-MEZEL S A R, AL-SOLAMY F R M, ANSARI Q H, ed. Fixed Point Theory, Variational Analysis and Optimization. Boca Raton: CRC Press, Taylor & Francis Group, 2014.