引 言
为了建立以数学物理方法为基础的数值天气预报,文献[1]首先引入了大气原始方程组和海洋原始方程组．空间科学技术(雷达)、气象卫星和计算机技术等一大批近代科学技术的日益成熟,为人们利用大气原始方程组和海洋原始方程组来预报天气和气候提供了强力的技术保证,数值天气预报迎来蓬勃发展的时代．更多关于大气、海洋原始方程组的发展介绍可以参看文献[2]．在对基于大气、 海洋原始方程组的数值天气预报模式进行研究时,人们主要关心的是这些方程组在数学上是否具有内在的逻辑统一性,即适定性．在这方面的研究已经持续了很长一段时间,出现了大量的成果[3-14]．
与上述文献不同,本文研究海洋动力学中二维黏性方程组解对热源的收敛性, 即研究当热源趋近于零时对方程组的解带来的影响．因为在建立数学模型的过程中不可避免地会出现一些微小的误差,我们需要知道这些误差会不会引起方程组解的巨大变化．用数学分析的方法来研究方程组的连续依赖性或收敛性是非常具有实际意义的,并且这种性质已经赢得了一个名字——结构稳定性．结构稳定性的概念最先由Hirsch和Smale[15]提出，有关结构稳定性的本质可参见文献[16]．在过去的几十年中,很多文献都在研究各种类型的偏微分方程组的连续依赖性或收敛性,他们的研究主要集中在Brinkman、Darcy、Forchheimer方程组和Navier-Stokes方程组[17-23]．据笔者所知,目前几乎还没有文章关注海洋动力学中二维黏性原始方程组的连续依赖性或收敛性,由于我们研究的模型是高度非线性的,因此本文的分析也是非平凡的,并可为其他类型的原始方程组的研究提供借鉴．
二维黏性海洋原始方程组主要由质量、动量、能量守恒方程和盐度守恒方程组成,可以表示为
(1)
其中Ω=(0,h1)×(-h2,0),h1,h2是大于零的常数;未知函数(u,v),w,ρ,p,T分别表示水平速度场、垂直速度、密度、压强和温度； f是地球自转的函数,这里取常数；μi>0(i=1,2,3)是黏度系数； ρ0,T0是密度和温度的参考值； βT是膨胀系数(常数),
是给定热源函数．海洋原始方程组(1)中还应包括盐度方程,但由于盐度方程和热量方程类似,并不会为本文带来额外的难度,故方程组(1)中忽略了盐度方程．
区域Ω的边界记为∂Ω并分为3个部分：
于是系统(1)的边界条件可以写为
(2)
其中β是一个大于零的常数．此外,方程组的初始条件为
u(x,z,0)=u0(x,z), v(x,z,0)=v0(x,z), T(x,z,0)=T0(x,z), in Ω，
(3)
其中u0,v0,T0是给定的函数．
本文的结构如下: 第1节给出了一些准备工作,并列举或证明一些本文常用的Soblev不等式；第2节受文献[24-26]的启发,推导了依赖于方程组的系数、初边值条件以及区域的几何性质的严格先验界；第3节推导了方程组对热源的收敛性；最后，第4节是全文的总结．
1 准 备 工 作
因为w|z=-h2=0,对式(1)的第四个方程从-h2到z积分,可得
(4)
又因为w|z=0=0,则
(5)
所以当0≤x≤h1时，
u(x,ζ,t)dζ是一个常数．再注意到式(2)中的第三个条件,有
u(x,ζ,t)dζ=0, ∀0≤x≤h1．
对式(1)的第三个方程从z到0积分并利用式(1)的第六个方程以及边界条件(2),有
(6)
其中ps=p(x,0,t)表示海洋表面的压强, μ=ρ0βT．把式(4)和(6)代入到式(1)～(3)中,不失一般性，假设μ=μi=1(i=1,2,3)，该问题可以写为
(7)
边界条件为
(8)
初始条件为
(u,v,T)|t=0=(u0,v0,T0)．
(9)
接下来我们给出一些本文常用的微分不等式．
引理1[27-28] 若ω(x)∈C1(0,h)并且ω(0)=ω(h)=0,则
(10)
引理2 若ω(x,z,t)是区域Ω=(0,h1)×(-h2,0)中充分光滑的函数,且ω(0,z,t)=ω(h1,z,t)=0,则
即
其中=(∂x,∂z),C是一个大于零的常数,δ是一个大于零的任意常数．
证明 应用Hölder不等式,可得
(11)
因为
ω(0,z,t)=ω(h1,z,t)=0,
所以
于是
(12)
把式(12)代入到式(11),可得
(13)
另一方面,有
(14)
则
(15)
为了控制式(15)的最后一项,定义一个新函数f(x2)，满足
f(0)>0, f(-h2)<0, |f′(z)|≤m1, |f(z)|≤m2, -h2≤z≤0,
(16)
其中m1,m2是大于零的常数．例如, f(z)=(m1/2)(z+h2/2),m1h2<4m2满足式(16)中的所有条件．再利用散度定理,可得
min{f(0),-f(-h2)}[ω2(x,0,t)+ω2(x,-h2,t)]≤
f(0)ω2(x,0,t)-f(-h2)ω2(x,-h2,t)=
(17)
把式(17)代入到式(15),有
(18)
其中
所以
(19)
结合式(13)和(19),并利用Hölder不等式,有
取δ=1,对上式简化之后,可得
(20)
应用分部积分,我们易得以下引理．
引理3 若
则
其中g(z,t)是[-h2,0]上不依赖于x的连续函数．
2 先 验 界
引理4 若T0, Q∈L∞(Ω),则式(7)第三个方程的解T满足
(21)
其中 Tm=supΩ{‖Q‖∞, ‖T0‖∞}．
证明 在方程(7)第三个方程的两边乘以Tp-1,并在Ω上积分可得
(22)
应用引理3可知式(22)的右端第三项等于零．由Hölder不等式和Cauchy-Schwarz不等式,有
(23)
所以
(24)
由Gronwall不等式,可得
所以
(25)
在式(25)中令p→∞,可得
(26)
在式(24)中取p=2,有
(27)
再次利用Gronwall不等式我们可以得到以下引理．
引理5 假设T是方程组(7)～(9)的解,且T0, Q∈L2(Ω)．则
T|2dAdη≤F1(t),
其中
引理6 设(u,v)为方程组(7)～(9)的解,且u0, v0, T0∈L2(Ω)．则
v|2dAdη≤F2(t),
其中
证明 取式(7)中的第一个方程和u在L2(Ω)上的内积,有
u|2dA=
(28)
应用引理3,并对式(28)的右端第四项实施Cauchy-Schwarz不等式,可得
(29)
于是再由引理5，有
(30)
同理由式(7)的第二个方程可得
(31)
联合式(30)和(31)并使用式(8),可得
(32)
对式(32)从0到t积分,可得
v|2dAdη≤F2(t)．
(33)
引理7 设(u,v)为方程组(7)～(9)的解,且∂zu0, ∂zv0, T0∈L2(Ω)．则
其中
证明 将式(7)的第一个方程对z求导,并与∂u/∂z在L2(Ω)上取内积,有
(34)
即
(35)
利用引理3,并对式(35)的最后一项实施Hölder不等式以及引理5和引理6,可得
因此
(36)
类似地,重复上述过程可得
(37)
应用Cauchy-Schwarz不等式、引理2和引理6，有
(38)
其中δ1, δ2, δ3是任意的大于零的常数． 把式(38)代入到式(37)然后令式(36)和(37)相加, 并取
有
其中
(39)
利用引理3(δ=1)、引理6和引理7，有
(40)
3 对热源的收敛性
设
是当Q=0时方程组(7)～(9)的一组解．定义
(41)
则
满足
(42)
边界条件可以写为
(43)
初始条件为
(44)
定理1 设
是方程组(42)～(44)的解,且T0∈L∞(Ω)以及T0,u0,v0∈L2(Ω)．则对γ(t)>0满足
(45)
此式表明了方程组(7)～(9)的解对热源Q的收敛性．
证明 取式(42)中的第二个方程与
在L2(Ω)上的内积,有
(46)
对式(46)的右端第二项和第五项实施引理3,对右端第三项实施分部积分和Cauchy-Schwarz不等式,有
(47)
对右端第四项实施Hölder不等式、引理2、引理6和式(40),有
(48)
其中b1(t),b2(t)是大于零的可加性函数, δ4是一个大于零的任意常数．基于上述结果,取δ4=1/(8b2(t))，则式(46)可以写为
(49)
现在取式(42)中的第二个方程与
在L2(Ω)上的内积,有
(50)
经过与式(49)同样的计算,易得
(51)
其中b3(t),b4(t)是一个大于零的函数,δ5是一个大于零的任意常数．联合式(49)和(51)并取δ5=1/(8b4(t)),可得
(52)
取式(42)的第三个方程与
在L2(Ω)上的内积,有
(53)
利用分部积分、Hölder不等式、引理4、引理5和算术几何平均不等式，有
(54)
再由Hölder不等式和算术几何平均不等式,可得
(55)
对式(53)中的右端第二项实施引理3,然后把式(54)和(55)代入到式(53),可得
(56)
接下来,在式(52)的两边乘以
再和式(56)相加,可得
(57)
其中
所以
(58)
对式(58)从0到t积分
(59)
再将式(59)代入到式(57)即可完成定理1的证明．
4 总 结
本文对海洋动力学中原始方程组中的热源进行了收敛性分析．通过推导方程组的先验界,引入辅助函数,证明了方程组的解对热源具有收敛性．大多文献主要关注原始方程组的适定性,本文的研究是对文献的一个有益补充,而且这方面的研究还可以持续下去．比如下一步可以继续研究方程组对黏性系数的收敛性,在“能量”函数中必然会缺少‖
这会对式(48)的推导带来一定的困难,这将是接下来研究的一个方向．
[1] RICHARDSON L F. Weather Prediction by Numerical Press[M]. Cambridge: Cambridge University Press, 1922.
[2] 郭柏灵, 黄代文, 黄春研. 大气、海洋动力学中一些非线性偏微分方程的研究[J]. 中国科学: 物理学 力学 天文学, 2014, 44(12): 1275-1285.(GUO Boling, HUANG Daiwen, HUANG Chunyan. Study on some partial differential equations in the atmospheric and oceanic dynamics[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2014, 44(12): 1275-1285.(in Chinese))
[3] ZENG Q C. Mathematical and Physical Basis of Numerical Weather Prediction[M]. Beijing: Science Press, 1979.
[4] LIONS J L, TEMAM R, WANG S. New formulations of the primitive equations of atmosphere and applications[J]. Nonlinearity, 1992, 5: 237-288.
[5] LIONS J, TEMAM R, WANG S. On the equations of the large-scale ocean[J]. Nonlinearity, 1999, 5: 1007-1053.
[6] SUN J Y, CUI S B. Sharp well-posedness and ill-posedness of the three-dimensional primitive equations of geophysics in Fourier-Besov spaces[J]. Nonlinear Analysis: Real World Applications, 2019, 4: 445-465.
[7] HIEBER M, HUSSEIN A, KASHIWABARA T. Global strong Lp well-posedness of the 3D primitive equations with heat and salinity diffusion[J]. Journal of Differential Equations, 2016, 261(12): 6950-6981.
[8] YOU B, LI F. Global attractor of the three-dimensional primitive equations of large-scale ocean and atmosphere dynamics[J]. Zeitschrift für Angewandte Mathematik und Physik, 2018, 69: 114. DOI: 10.1007/s00033-018-1007-9.
[9] CHIODAROLI E, MICH
LEK M. Existence and non-uniqueness of global weak solutions to inviscid primitive and Boussinesq equations[J]. Communications in Mathematical Physics, 2017, 353: 1201-1216.
[10] SUN J Y, YANG M. Global well-posedness for the viscous primitive equations of geophysics[J]. Boundary Value Problems, 2016, 2016: 21. DOI: 10.1186/s13661-016-0526-6.
[11] SUN J Y, CUI S B. Sharp well-posedness and ill-posedness of the three-dimensional primitive equations of geophysics in Fourier-Besov spaces[J]. Nonlinear Analysis: Real World Applications, 2019, 48: 445-465.
[12] GUO B L, HUANG D W. On the 3D viscous primitive equations of the large-scale atmosphere[J]. Acta Mathematica Scientia, 2009, 29(4): 846-866.
[13] 李振邦. 一类非局部Cahn-Hilliard方程弱解的存在唯一性[J]. 纯粹数学与应用数学, 2019, 35(1): 15-33.(LI Zhenbang. The existence and uniqueness of solutions for a nonlocal convextive Cahn-Hilliard equation[J]. Pure and Applied Mathematics, 2019, 35(1): 15-33.(in Chinese))
[14] 王欣, 郭科. 一类非凸优化问题广义交替方向法的收敛性[J]. 应用数学和力学, 2018, 39(12): 1410-1425.(WANG Xin, GUO Ke. Convergence of the generalized alternating direction method of multipliers for a class of nonconvex optization problrms[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1410-1425.(in Chinese))
[15] HIRSCH M W, SMALE S. Differential Equations, Dynamical Systems and Linear Algebra[M]. New York: Academic Press, 1974.
[16] AMES K A, STRAUGHAN B. Non-Standard and Improperly Posed Problems[M]. Mathematics in Science and Engineering Series: Vol 94. San Diego: Academic Press, 1997.
[17] LIU Y. Continuous dependence for a thermal convection model with temperature-dependent solubitity[J]. Applied Mathematics and Computation, 2017, 308: 18-30.
[18] LIU Y, XIAO S, LIN C. Continuous dependence for the Brinkman-Forchheimer fluid interfacing with a Darcy fluid in a bounded domain[J]. Mathematics and Computers in Simulation, 2018, 150: 66-82.
[19] LIU Y, DU Y, LIN C. Convergence results for Forchheimer’s equations for fluid flow in porous media[J]. Journal of Mathematical Fluid Mechanics, 2010, 12(4): 576-593.
[20] SCOTT N L. Continuous dependence on boundary reaction terms in a porous medium of Darcy type[J]. Journal of Mathematical Analysis and Applications, 2013, 399: 667-675.
[21] SCOTT N L, STRAUGHAN B. Continuous dependence on the reaction terms in porous convection with surface reactions[J]. Quarterly of Applied Mathematics, 2013, 71: 501-508.
[22] LI Y, LIN C. Continuous dependence for the nonhomogeneous Brinkman-Forchheimer equations in a semi-infinite pipe[J]. Applied Mathematics and Computation, 2014, 244: 201-208.
[23] HAMEED A A, HARFASH A J. Continuous dependence of double diffusive convection in a porous medium with temperature-dependent density[J]. Basrah Journal of Science, 2019, 37: 1-15.
[24] CAO C, TITI E S. Global well-posedness of the three-dimensional viscous primitive equations of large scale ocean and atmosphere dynamics[J]. Annals of Mathematics, 2007, 166: 245-267.
[25] 黄代文, 郭柏灵. 关于海洋动力学中二维的大尺度原始方程组
[J]. 应用数学和力学, 2007, 28(5): 521-531.(HUANG Daiwen, GUO Boling. On two-dimensional large-scale primitive equations in oceanic dynamics[J]. Applied Mathematics and Mechanics, 2007, 28(5): 521-531.(in Chinese))
[26] 黄代文, 郭柏灵. 关于海洋动力学中二维的大尺度原始方程组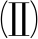
[J]. 应用数学和力学, 2007, 28(5): 532-538.(HUANG Daiwen, GUO Boling. On two-dimensional large-scale primitive equations in oceanic dynamics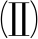[J]. Applied Mathematics and Mechanics, 2007, 28(5): 532-538.(in Chinese))
[27] HARDY C H, LITTLEWOOD J E, POLYA G. Inequalities[M]. Cambridge: Cambridge University Press, 1953.
[28] MITRONOVIC D S. Analytical Inequalities[M]. Springer-Verlag, 1970.