引 言
复合材料层合板壳结构的面外应力对于层间分层的起始和扩展具有重要影响.为了模拟面外应力沿厚度方向的非线性分布,前人提出了许多解析方法和数值方法.由于理论公式比较简单、计算资源消耗低且适应任何复杂的工程结构,位移有限元法具有吸引力.但是,若采用较粗的网格,常规的位移法难以给出复合材料结构面外应力的理想结果.一方面,因为位移法的应力结果是基于本构关系通过假设的位移插值函数的微分得到的,应力结果的精度比位移结果的精度低一阶次.另一方面,由于位移法只有位移是独立假设的,当板厚变得很薄时,会出现剪切锁定现象,即使应用高阶层合板理论[1-2]也很难得到比较准确的沿厚度方向的面外剪切应力.特别指出:如果不对相邻单元于同一节点上的应力结果进行磨平处理,位移法的结果很难满足复合材料层合结构面外应力的连续性要求.
假设应力和位移两类变量的杂交应力元法[3-5]的应力结果是根据光滑的应力模式得到的.这是杂交应力元法的应力结果比较准确的主要原因之一.专著[3]中根据状态空间理论建立的部分杂交应力元法完全满足层间面外应力的连续性要求.有关位移法和杂交应力元法求解复合材料层合板/壳应力问题的调查分析可以参考文献[1-6].
将空间坐标z类比为时间度量,H-R变分原理的Reissner函数等价于Hamilton原理[7].这正是半解析的Hamilton部分混合元[8-10]的理论基础.Hamilton部分混合元包含了3个位移分量和全部面外应力分量,均采用相同的插值多项式.该混合元的主要优点包括:1) 满足面外应力的层间连续性要求和面外应力的边界条件,同时满足面内应力和面外应变的层间不连续性要求; 2) 可同时获得高精度的位移结果和面外应力结果.但是,就目前的发展情况来说,这类模型要求网格模型中同一子层内所有单元的厚度相同.因此,不适合厚度不均匀或几何形式比较复杂的复合材料层合结构.另一方面,对应Hamilton部分混合元的状态空间模型是线性微分方程系统,求解位移和应力之前,首先需要进行比较耗时的矩阵指数运算,不适应大规模的有限元分析.
当然,包含位移变量和应力变量的经典混合有限元法[11-12]为同时引入应力边界条件和位移边界条件提供了方便,并可同时获得精度比较高的位移和应力数值结果.因为混合有限元法中位移变量和应力变量的插值多项式相同,所以其位移和应力解的精度是一致的.这也是该类方法的应力结果比较准确的原因之一.一般情况下,经典混合有限元法的线性系统是非正定的(因为主对角线上存在零元素).因此,若不考虑稳定混合元技术方案[11-12],数值结果是不稳定的.附加稳定技术方案混合元的数学模型比较复杂,不易被工程师们所接受.这可能是经典混合法未能得到充分发展和广泛应用的原因之一.另一方面,通过全混合元(包括位移、面外应力和面内应力的所有分量)对应的有限元线性方程系统求得的全部应力分量结果与位移结果相同,于材料界面间均是连续的.然而,由于复合材料层合板壳结构各层材料不同,面内法向应力分量于层间通常是不连续的.因此,全混合法不适应复合材料层合板壳结构的应力分析.
为了更合理、更准确地分析复合材料层合板的层间面外剪切应力,Liao和Tsai[13]提出了部分混合有限元法,其中假定了全部位移分量和两个面外剪切应力分量,因而降低了混合有限元线性系统的自由度,提高了计算效率.但是,这种模型忽略了面外法向应力于层间的连续性要求.
最近,对文献[14]基于修正的H-R变分原理和势能原理建立了包含3个位移和全部面外应力分量的8节点非协调六面体辛元,其有限元线性系统对称保辛,并且系数矩阵主对角线上不存在零元素.与经典混合法和Hamilton部分混合元法相同,该辛元满足层合结构层间面外应力的连续性要求,通过其有限元线性系统求得的面外应力结果于节点处自然连续.与Hamilton部分混合元不同的是:该辛元所涉及的变量在3个坐标方向均被离散处理,对单元的厚度和几何形状没有限制.文献[15]从修正的广义H-R 变分原理出发,建立了求解复合材料层合板稳态温度场静力学问题的非协调8节点辛元,是文献[14]中辛元的扩展和应用.这两类辛元的共同缺点是:由于单元内非协调位移项的引入,需要对每个单元非协调部分的“刚度矩阵”求逆后方可消去内部节点的位移参数,该操作过程消耗大量的时间.
本文的主要目的是建立形式比较简单、效率较高的20节点六面体等参辛元,并用其分析复合材料层合板的应力.
1 基 本 理 论
1.1 最小势能原理
若不考虑体积力,最小势能原理可表示为
![]()
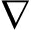 u)TC(
u)TC(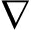
![]()
(1)
式中,V为弹性体的体积,S为结构的表面积,C表示材料的刚度矩阵,u=[u v w]T是关于3个方向(x1,x2,x3)的位移向量,![]() 为表面Sσ上的外载荷,
为表面Sσ上的外载荷,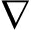 是阶数为6×3的微分算子矩阵.
是阶数为6×3的微分算子矩阵.
1.2 20节点位移单元的刚度矩阵
三维六面体位移单元的位移变量u可表示为
u=Nqe,
(2)
式中,qe=[u1e u2e u3e]T表示单元节点的位移向量;N为对角矩阵,diag N=[Ne Ne Ne]T, Ne=[N1 N2 … N20]为等参形式的20节点插值多项式.
将式(2)代入式(1),考虑位移向量qe的变分,则单元的刚度方程为
Dqqqe=fq,
(3)
其中![]()
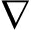 N)TC(
N)TC(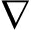
![]()
1.3 修正的H-R变分原理
假设边界的位移![]() 事先满足,则修正的H-R变分原理[7-10,14](忽略体积力)为
事先满足,则修正的H-R变分原理[7-10,14](忽略体积力)为
(4)
其中LMHR是Reissner能密度函数:
![]()
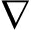 2u)TΦ22
2u)TΦ22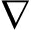 2u,
2u,
(5)
式中,σo=[σxz σyz σzz]T是面外应力向量;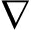 1,
1,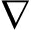 2和
2和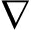 3是微分算子矩阵;Φ11,Φ21和Φ22是材料参数矩阵.
3是微分算子矩阵;Φ11,Φ21和Φ22是材料参数矩阵.
面内应力σi=[σxx σyy σxy]T可由位移和面外应力表示:
σi=φ21σo+φ22(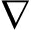 2u).
2u).
(6)
1.4 20节点辛元
与文献[14-15]相同,面外应力可表示为
σo=Npe,
(7)
其中,pe=[σ13e σ23e σ33e]T为单元节点的面外应力向量.
将式(2)和(7)代入式(4)可得修正的H-R变分原理的离散形式:
(8)
其中
![]()
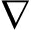 1N+Φ21
1N+Φ21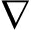 2N+
2N+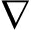 3N)dV,
3N)dV,
![]()
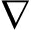 2N)TΦ22(
2N)TΦ22(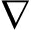 2N)dV,
2N)dV,
fq的积分式与式(3)中fq的积分式相同.
将pe和qe视为相互独立的变量,由δΠMHR(pe,qe)=0可得
(9)
这里必需说明:式(8)和(9)中的Kqq的主对角线上含有零元素(因为微分算子矩阵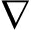 2的主对角线上有零元素).实践表明:与经典的混合法一样,如果简单地考虑式(9)取和后的控制方程来求解具体问题,位移和应力结果并不随着网格的增加稳定地收敛.
2的主对角线上有零元素).实践表明:与经典的混合法一样,如果简单地考虑式(9)取和后的控制方程来求解具体问题,位移和应力结果并不随着网格的增加稳定地收敛.
为了消去式(9)中主对角线上的零元素,将其与式(3)合并,则有
(10a)
其中
交换上式的行,可得
(10b)
显然,式(10b)与文献[14]中非协调辛元在形式上完全相同,满足辛空间Hamilton矩阵的定义.因此,这里称式(10b)为20节点等参辛元.
2 数 值 算 例
算例1 考虑三层的矩形层合梁[0°/90°/0°].层合板总厚度为H=0.1,上中下三层厚度均为H/3,长a=4H.各层的材料参数[16]为:E11=25E22=25E33,G12=G13=0.5E33,G23=0.2E33,μ12=μ13=μ23=0.25.该梁的两端简支约束(当x1=0和x1=a时,σ11=u2=u3=0).上表面(x3=0.1处)垂直方向施加了单向正弦载荷q=q0sin(πx1/a).
因为几何模型、位移边界条件和载荷均是对称的,因此考虑1/4对称模型:x1方向划分为9个单元;x2方向划分为1个单元;每层厚度方向(x3)划分为2个单元,共54个单元.20节点位移元(CDE20)和20节点辛元(CSE20)采用相同的有限元模型.
图1和图2分别为面外应力![]() 和
和![]() 沿厚度方向的分布.图1~8图例中的CDE20代表20节点位移元,其应力结果是根据材料的本构关系计算Gauss点的应力, 然后用外推方法得到节点上的应力, 最后对相邻单元同一个节点应力值取平均值; CSE20代表本文20节点辛元, 面外应力结果和位移结果通过式(10)求得.图1~3中EXACT(精确解)取自文献[16].
沿厚度方向的分布.图1~8图例中的CDE20代表20节点位移元,其应力结果是根据材料的本构关系计算Gauss点的应力, 然后用外推方法得到节点上的应力, 最后对相邻单元同一个节点应力值取平均值; CSE20代表本文20节点辛元, 面外应力结果和位移结果通过式(10)求得.图1~3中EXACT(精确解)取自文献[16].
图1~8中各应力分量的结果采用了如下的无量纲公式:
(11a)
(11b)
式中,q0表示载荷,S表示长厚比.算例1中的S=a/H=4.
在相同的有限元网格条件下,图1表明本文辛元的面外剪切应力![]() 比位移元的面外剪切应力
比位移元的面外剪切应力![]() 更贴近精确解.事实上,CSE20的结果与精确解的最大误差小于1%.图2、3表明辛元和位移元的结果差别甚微.不难看出,面外法向应力
更贴近精确解.事实上,CSE20的结果与精确解的最大误差小于1%.图2、3表明辛元和位移元的结果差别甚微.不难看出,面外法向应力![]() 和面内法向应力
和面内法向应力![]() 沿厚度方向的非线性分布特性不显著.
沿厚度方向的非线性分布特性不显著.
算例2 考虑三层的矩形层合板[0°/90°/0°].层合板总厚度为H=0.1,上中下三层厚度均为H/3,长a=10H,宽b=a.各层材料参数[17]为:E11=E22=4×104,E33=5×105,G13=G23=6×104,G12=1.6×104,μ12=μ13=μ23=0.25.层合板为四边简支约束:当x1=0和x1=a时,σ11=u2=u3=0;当x2=0和x2=b时,σ22=u1=u3=0.上表面(x3=0.1处)垂直方向施加均布载荷q0.本例中用于无量纲化的S=a/H=10.
考虑1/4对称的有限元模型:x1和x2方向各6个单元;每层厚度方向(x3)2个单元.图4~10中EXACT(精确解)采用了文献[17]中的方法求得.
图![]() 沿厚度的分布 图
沿厚度的分布 图![]() 沿厚度的分布
沿厚度的分布
Fig.1 Distribution of ![]() along Fig.2 Distribution of
along Fig.2 Distribution of ![]() along
along
the thickness the thickness
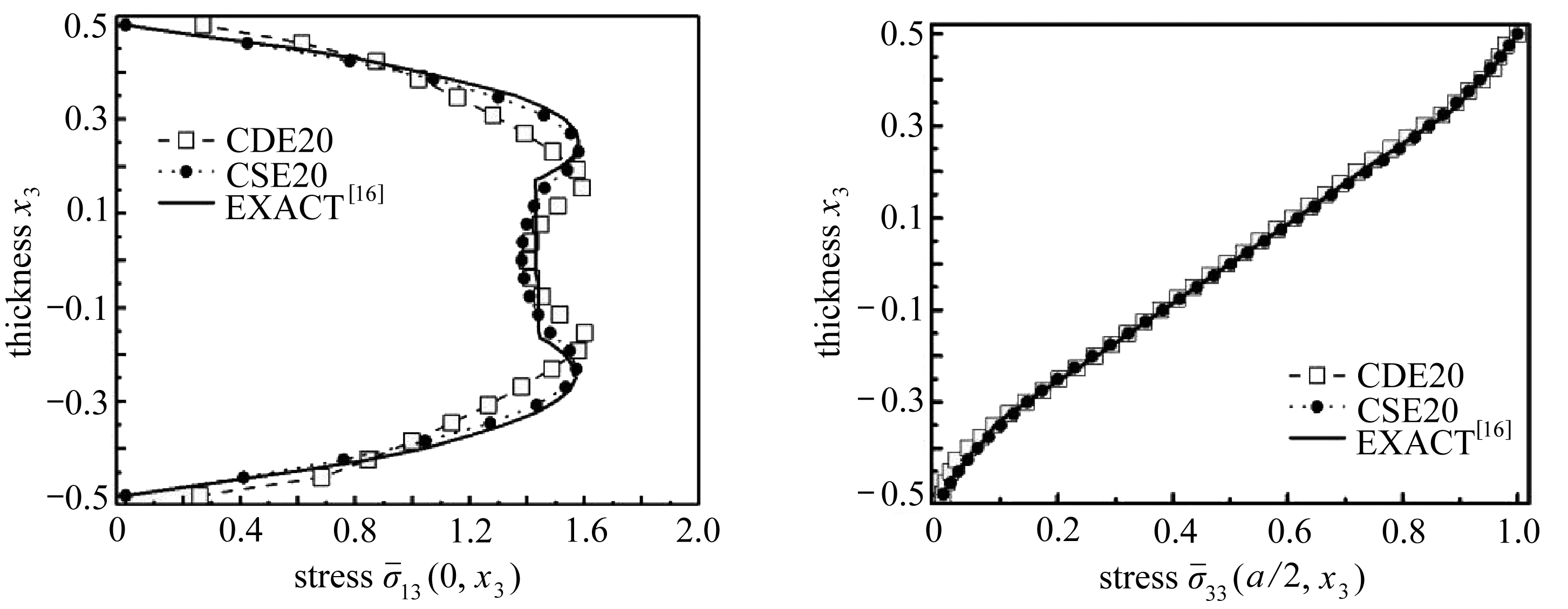
图![]() 沿厚度的分布 图
沿厚度的分布 图![]() 沿厚度的分布
沿厚度的分布
Fig.3 Distribution of ![]() along Fig.4 Distribution of
along Fig.4 Distribution of ![]()
the thickness the thickness
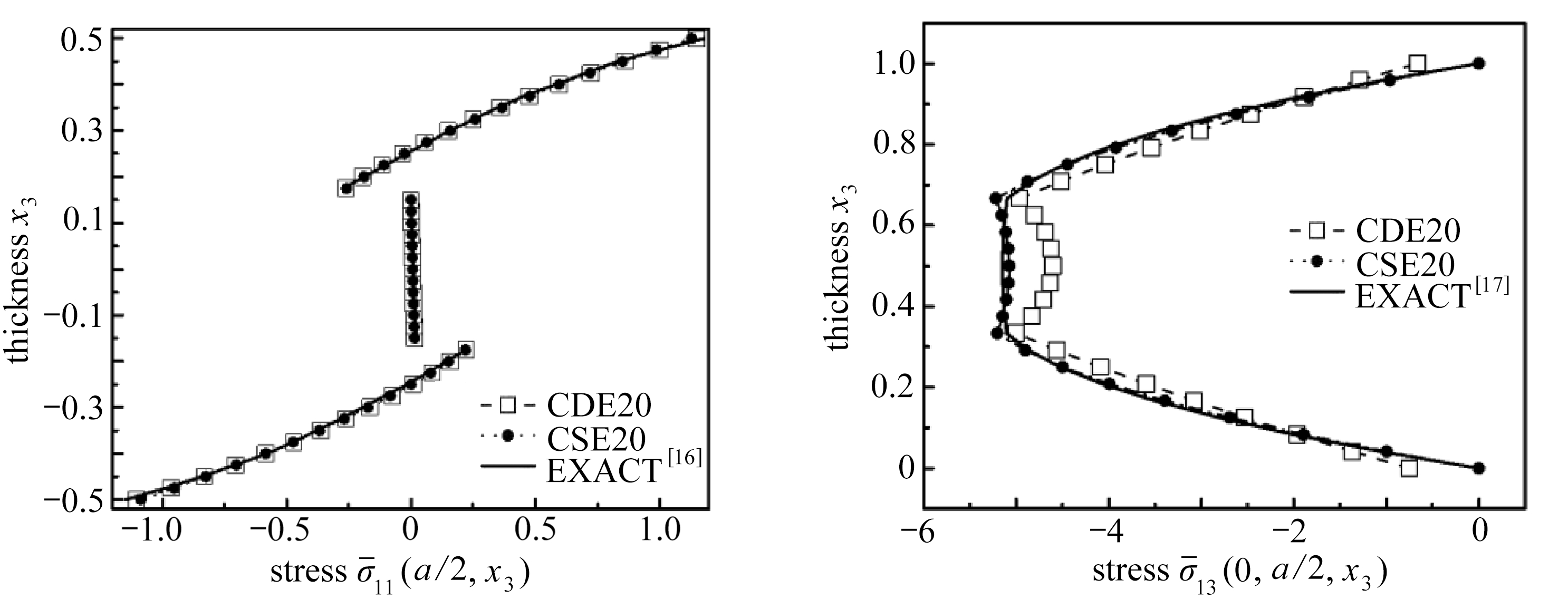
图![]() 沿厚度的分布 图
沿厚度的分布 图![]() 沿厚度的分布
沿厚度的分布
Fig.5 Distribution of ![]() 6 Distribution of
6 Distribution of ![]()
along the thickness along the thickness

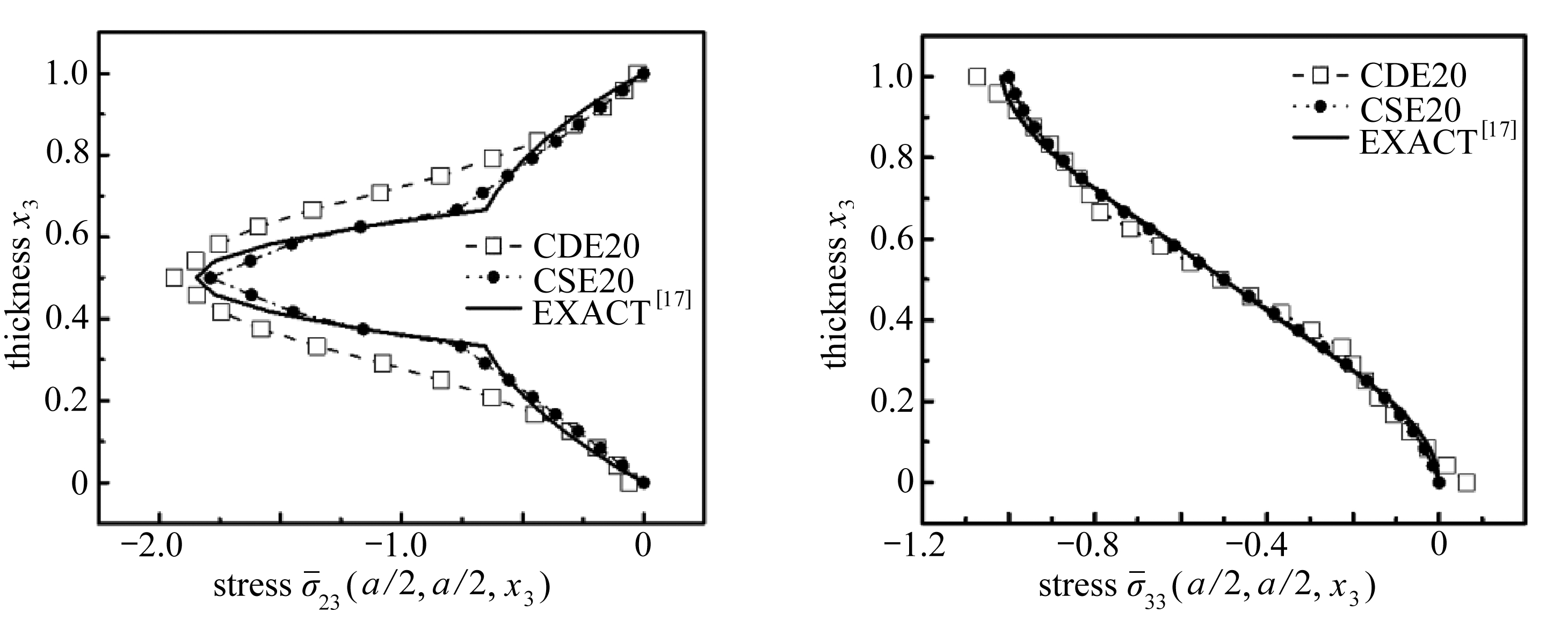
图![]() 沿厚度的分布 图
沿厚度的分布 图![]() 沿厚度的分布
沿厚度的分布
Fig.7 Distribution of ![]() 8 Distribution of
8 Distribution of ![]()
along the thickness along the thickness
由图4和图6可以看出,算例2进一步表明辛元(CSE20)的面外剪切应力![]() 和
和![]() 的结果分别比20节点位移元(CDE20)的结果更接近精确解.
的结果分别比20节点位移元(CDE20)的结果更接近精确解.
同时,该例题表明,层合板面外法向应力![]() 面内法向应力
面内法向应力![]() 和面内剪切应力
和面内剪切应力![]() 沿厚度方向的非线性分布特性不显著.20节点辛元的这些应力结果比20节点位移元的结果相对理想,参见图6~8.20节点辛元的面外应力
沿厚度方向的非线性分布特性不显著.20节点辛元的这些应力结果比20节点位移元的结果相对理想,参见图6~8.20节点辛元的面外应力![]() 与精确解的误差为1.27%,是面外应力中的最大误差.
与精确解的误差为1.27%,是面外应力中的最大误差.
图9和10中的数据结果采用以下公式进行了无量纲化处理:
(12)
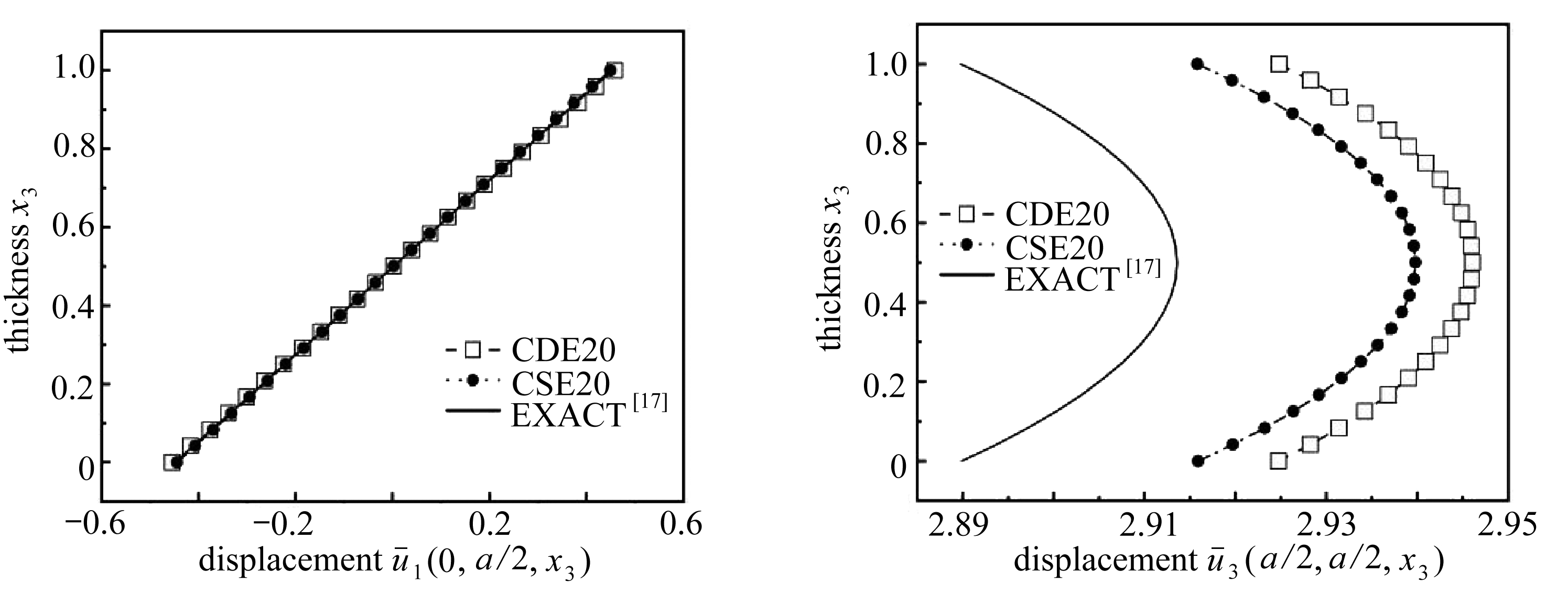
图![]() 沿厚度的分布 图
沿厚度的分布 图![]() 沿厚度的分布
沿厚度的分布
Fig.9 Distribution of ![]() 10 Distribution of
10 Distribution of ![]()
along the thickness along the thickness
20节点辛元的位移![]() 与精确解的误差为0.82%,是位移的最大误差.
与精确解的误差为0.82%,是位移的最大误差.
3 结 论
1) 本文推导20节点六面体辛元时已说明面外应力变量和位移变量采用了相同的高次插值函数.因此,没有必要再引入单元内部非协调位移.正因如此,与文献[14-15]中建立8节点六面体非协调辛元的过程比较,本文的推导过程非常简便.另一方面,与基于最小余能原理的经典应力元比较,本文应力变量的插值多项式不需要满足平衡方程,形式简单.
2) 20节点辛元避免了传统混合法中系数矩阵主对角线上含有零元素的弊端,因而保证了其有限元线性系统数值结果的精度和稳定性.
3) 由于3个坐标方向均被离散处理,因此本文的20节点辛元对分析对象的几何形状没有限制.
4) 辛元的有限元线性系统包含了位移和应力两类变量,为面外应力边界条件的引入提供了方便.数值实例表明,20节点辛元面外应力结果的精度和位移结果的精度比较接近.
[1] REDDY J N.A simple higher-order theory for laminated composite plates[J].Journal of Applied Mechanics, 1984, 51(4): 745-746.
[2] NOOR A K, BURTON W S.Assessment of shear deformation theories for multilayered composite plates[J].Applied Mechanics Reviews, 1989,42(1): 1-13.
[3] PIAN T H H, WU C C.Hybrid and Incompatible Finite Element Methods[M].Chapman and Hall CRC, 2005.
[4] JING H S, LIAO M L.Partial hybrid stress element for the analysis of thick laminated composite plates[J].Computers & Structures, 1990, 36(1): 57-64.
[5] 田宗漱, 卞学鐄.多变量变分原理与多变量有限元方法[M].北京: 科学出版社, 2011.(TIAN Zhongshu, PIAN T H H.Variational Principle With Multi-Variables and Finite Element With Multi-Variables[M].Beijing: Science Press, 2011.(in Chinese))
[6] REDDY J N, ROBBINS D H.Theories and computational models for composite laminates[J].Applied Mechanics Reviews, 1994, 47(6): 147-169.
[7] 钟万勰.应用力学的辛数学方法[M].北京: 高等教育出版社, 2006.(ZHONG Wanxie.Symplectic Solution Methodology in Applied Mechanics[M].Beijing: Higher Education Press, 2006.(in Chinese))
[8] 唐立民, 褚致中, 邹贵平, 等.混合状态Hamilton元的半解析解和叠层板的计算[J].计算力学学报, 1992, 9(4): 347-360.(TANG Limin, CHU Zhizhong, ZOU Guiping, et al.The semi-analytical solution of mixed state Hamilton element and the computation of laminated plates[J].Chinese Journal of Computational Mechanics, 1992, 9(4): 347-360.(in Chinese))
[9] ZOU G P, TANG L M.A semi-analytical solution for laminated composite plates in Hamilton system[J].Computer Methods in Applied Mechanics and Engineering, 1995, 128(3/4): 395-404.
[10] QING G H, QIU J J, LIU Y H.Free vibration analysis of stiffened laminated plates[J].International Journal of Solids and Structures, 2006, 43(6): 1357-1371.
[11] ATLURI S N, GALLAGHER R H, ZIENKIEWICZ O C.Hybrid and Mixed Finite Element Methods[M].Chichester: Wiley, 1983.
[12] ARNOLD D N, FALK R S, WINTHER R.Mixed finite element methods for linear elasticity with weakly imposed symmetry[J].Mathematics of Computation, 2007, 76: 1699-1724.
[13] LIAO C L, TSAI J S.Partial mixed 3-D element for the analysis of thick laminated composite structures[J].International Journal For Numerical Methods in Engineering, 1992, 35(7): 1521-1539.
[14] QING G, TIAN J.Highly accurate symplectic element based on two variational principles[J].Acta Mechanica Sinica, 2018, 34(1): 151-161.
[15] 刘艳红, 李锐.含参数辛元与热弹性复合材料层合板分析[J].复合材料学报, 2019, 36(5): 1306-1312.(LIU Yanhong, LI Rui.Parametered symplectic element and analysis of thermoelastic composite laminates[J].Acta Materiae Compositae Sinica, 2019, 36(5): 1306-1312.(in Chinese))
[16] PAGANO N.Exact solutionsfor composite laminates in cylindrical bending[J].Journal of Composite Materials, 1969, 3(3): 398-411.
[17] 范家让.强厚叠层板壳的精确理论[M].北京: 科学出版社, 1996.(FAN Jiarang.Exact Theory of Laminated Thick Plates and Shells[M].Beijing: Science Press, 1996.(in Chinese))