引 言
脉冲微分方程基于传统的微分方程动力学模型,又借助于脉冲扰动来刻画系统的某些运动状态瞬时变化或跳跃的现象,同时研究瞬时变化对系统状态带来的影响.上述由微分动力系统耦合脉冲或离散时间而成的系统称为脉冲微分系统,它具有连续系统和离散系统的共有特征,所以脉冲微分系统能更加真实地反映自然状态下物种的变化规律和人为干预措施,并具有比普通微分方程更加丰富的性质和应用背景.特别地,渔业资源养殖的收获与投放、森林管理中的种植与砍伐、农业中的喷洒杀虫剂或定期投放天敌等许多人为干预因素,都需要借助脉冲微分方程来描述和研究.
在过去的几十年中,有效控制害虫已经变得十分复杂.综合害虫管理[1]利用所有适当的方法和技术,采用尽可能互相配合的方式来控制害虫,可以使害虫种群数量降低到经济、生态等各方面能容忍的水平之下.常用的控制方法有化学控制、生物控制和人工防治等.在实施害虫控制策略时,应该综合各种控制策略的优缺点,相互配合,从而实现最优的控制策略,这需要建立数学模型进行系统分析,特别是为设计最优的控制方案提供决策依据.近些年来,具有综合害虫控制策略的捕食与被捕食系统已经得到了广泛研究,并取得了很好的研究成果[2-11].上述研究中的一个主要假设是: 害虫的瞬时杀死率是依赖害虫种群当前数量的一个线性函数,而天敌的投放量也是一个常数.然而害虫综合控制策略的实施往往应该依赖害虫种群当前的数量,并受到农业资源有限的影响,即害虫的杀死率和天敌的投放量应该是基于种群数量的饱和函数.因此,将资源有限的非线性因素引入到模型里更加合理[12-14].文献[15]考虑了资源有限的非线性脉冲模型:
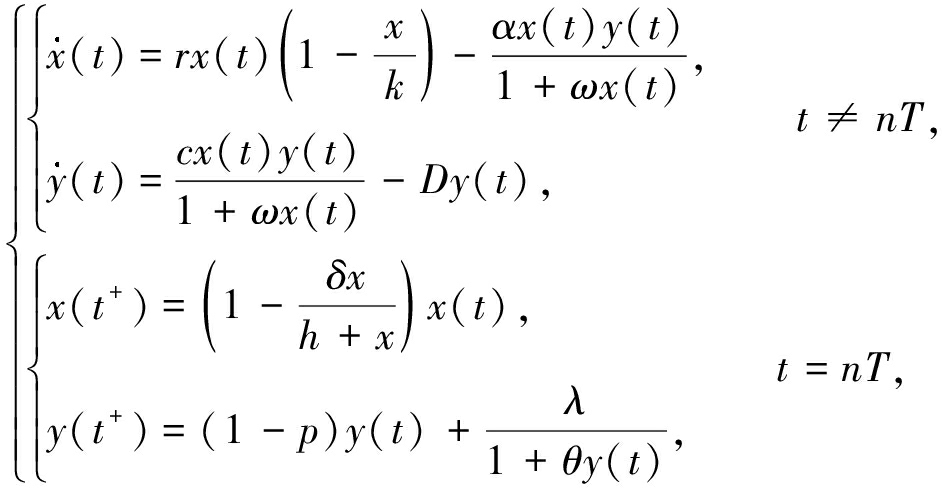
(1)
式中x(t)和y(t)分别表示在t时刻害虫和天敌的种群数量; r,k,c,D,α,ω,θ,h均为正常数; δ为喷洒杀虫剂对害虫的最大杀死率(0<δ≤1); h为半饱和常数; λ为投放天敌的最大数量; θ为形式参数; T是脉冲周期;p表示在nT时刻喷洒杀虫剂时天敌的杀死率.文献[15]研究了当p=0时,害虫灭绝周期解的全局稳定性,通过分支理论给出非平凡周期解存在的充分条件,数值上揭示了系统存在复杂的非线性动力学行为.然而杀虫剂杀死害虫比例过大或喷洒杀虫剂过于频繁会导致自然天敌种群灭绝,再者人为过度收获捕食者也会导致捕食者种群灭绝,因此为了更加合理地利用自然资源,需要考虑天敌灭绝周期解的存在性.本文聚焦参数λ=0和δ=1时模型(1)的动态行为,特别是系统(1)天敌灭绝周期解的全局稳定性,通过分支理论得到非平凡周期解存在的充分条件.最后,本文详细地数值分析探讨了当参数0<δ<1时,非线性脉冲如何影响系统的动力学行为.
1 预备知识和基本引理
令![]() 表示非负整数集.令f=(f1, f2)为系统(1)前两个方程的右端函数,显然f的光滑性保证了解的存在唯一性.令
表示非负整数集.令f=(f1, f2)为系统(1)前两个方程的右端函数,显然f的光滑性保证了解的存在唯一性.令![]() 在
在![]() 上连续,n∈N,且lim(t,y)→(nT+,x)V(t,y)=V(nT+,x)存在.
上连续,n∈N,且lim(t,y)→(nT+,x)V(t,y)=V(nT+,x)存在.
引理1 令X(t)=(x(t),y(t))是系统(1)的一个解,如果初值X(0+)≥0,那么对于所有t≥0都有X(t)≥0成立.进一步地,如果X(0+)>0,那么对于所有t>0都有X(t)>0.
引理2 令V∈V0,且有下面不等式成立:
其中g:R+×R+→R+在(nT,(n+1)T]上连续,lim(t,x)→(nT+,y)g(t,x)=g(nT+,y)存在,ψn:R+→R+为非递减的.令r(t)为标量脉冲微分方程
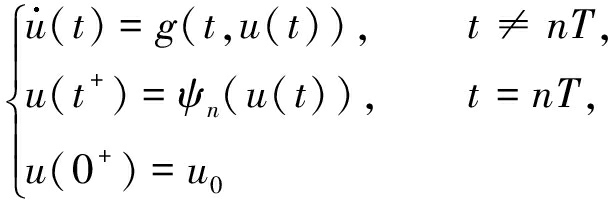
在[0,+∞)上的最大解,则对t≥0,当V(0+,x0)≥0时,V(t,x)≤r(t) .
首先,给出系统(1)的子系统

(2)
的基本性质.
引理3 当δ=1时,系统(2)存在一个正的全局稳定的周期解为
其中![]()
证明 由积分系统(2)的第一个方程有
所以
x((n+1)T+)=
F(x(nT+)).
(3)
令y((n+1)T+)=y(nT+),得到上面差分方程的唯一正稳点为
又因为
则
所以差分方程(3)的平衡态是局部稳定的,进一步根据函数F(x)的单增性和凸性,可知不动点也是全局稳定的,即系统(2)的周期解是全局稳定的.
引理4 当δ=1时,系统(1)存在一个天敌灭绝周期解:
其中![]()
2 天敌根除周期解的稳定性
定理1 如果
则系统(1)的天敌根除周期解(xp(t),0)是全局渐近稳定的.
证明 首先证明天敌根除周期解(xp(t),0)的局部稳定性.令u(t)=x(t)-xp(t),v(t)=y(t),其中u(t),v(t)为小的扰动.则系统(1)的线性化系统为

(4)
令φ(t)为系统(4)的基解矩阵,则φ(t)满足
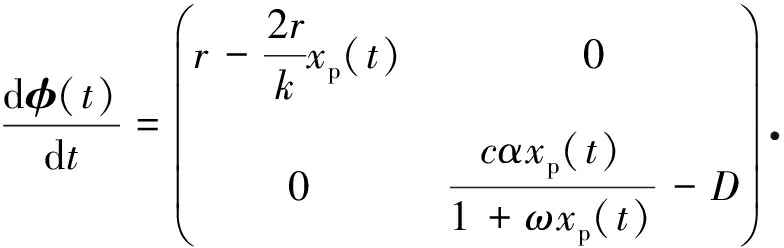
系统(4)在脉冲时刻的方程为
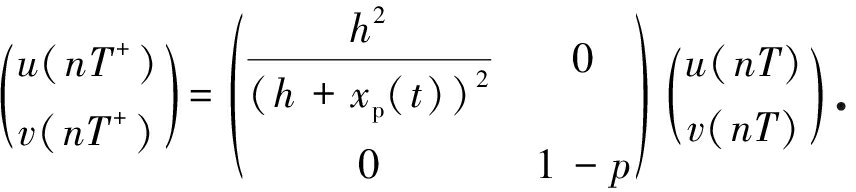
定义
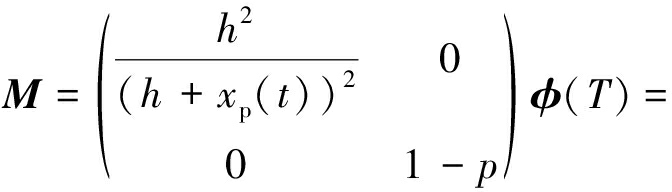
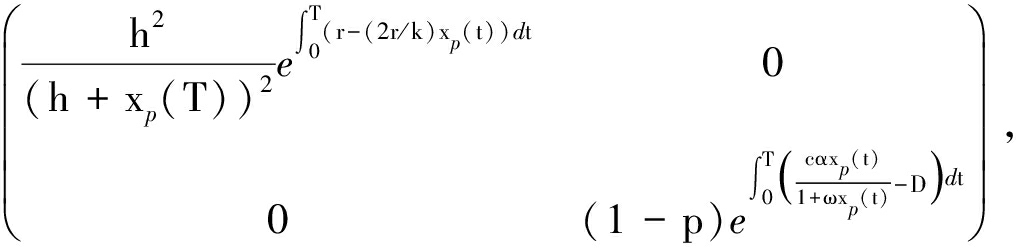
且记
为矩阵M的两个特征值.因为
所以
又因为
所以当
时, 系统(1)的天敌根除周期解(xp(t),0)是局部稳定的.
下面证明全局吸引性,取足够小的ε>0使得
由系统(1)的第一个方程得![]() 由引理2可得当t足够大时有x(t)≤xp(t)+ε,为了方便,假设对所有的t>0都有x(t)≤xp(t)+ε.进一步有
由引理2可得当t足够大时有x(t)≤xp(t)+ε,为了方便,假设对所有的t>0都有x(t)≤xp(t)+ε.进一步有

(5)
由脉冲微分方程比较定理得
(6)
因此![]() 即当n→∞时,y((n+l)T)→0.而当t∈((n+l)T,(n+l+1)T]时,0<x(t)≤(1-p)y((n+l)T)exp(cαT/ω),所以当t→∞时,y(t)→0.下面证明当t→∞时x(t)→xp(t).对任意的ε1>0,存在t1>0,当t>t1时有y(t)<ε1.由系统(1)的第一个方程有
即当n→∞时,y((n+l)T)→0.而当t∈((n+l)T,(n+l+1)T]时,0<x(t)≤(1-p)y((n+l)T)exp(cαT/ω),所以当t→∞时,y(t)→0.下面证明当t→∞时x(t)→xp(t).对任意的ε1>0,存在t1>0,当t>t1时有y(t)<ε1.由系统(1)的第一个方程有
由引理3得方程
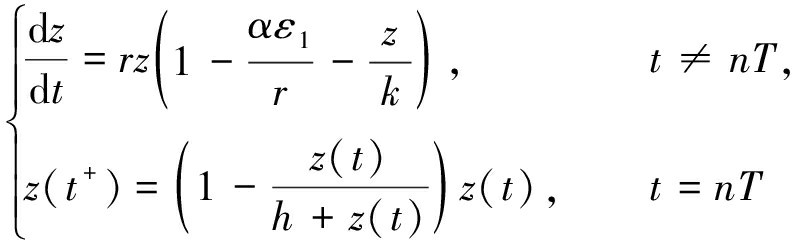
(7)
存在一个全局稳定的周期解
其中
由脉冲微分方程比较定理有z(t)≤x(t)≤xp(t)+ε,当t→∞时,z(t)→zp(t).所以对任意的ε>0,存在t2>0,当t>t2时有zp(t)-ε≤x(t)≤xp(t)+ε成立.令ε1→0,则xp(t)-ε≤x(t)≤xp(t)+ε,即t→∞时x(t)→xp(t).
3 非平凡周期解的存在性
下面讨论边界周期解不稳定的情况,令
则当阈值R(T)<0时,模型(1)的边界周期解全局稳定;当R(T)>0时边界周期解不稳定;下面讨论R(T)>0时模型(1)的动态行为,利用文献[16]中的分支理论得到如下主要结论.
定理2 如果R(T0)=0,则系统(1)在T0处发生超临界分支,当T>T0并且在T0附近时,系统(1)存在非平凡周期解.
证明 为了利用文献[16]的结论,记
令Φ为上面方程有关的流,从而X(t)=Φ(t,X0)(0<t≤T),其中X0=(x(0),y(0)),X(T)=Φ(T,X0),ξ(t)=(xp(t),0).由文献[16]有
容易得到
而且简单计算可得
其中T0为d0=0的根.若d0=0,则存在T0使得R(T0)=0.进一步计算得
c′0=0.
再求二阶偏导得
于是得到
令
则
又因为
所以有φ(T0)>0,这意味着B<0.所以BC<0,根据文献[16]中的定理2得知模型(1)在T0处发生超临界分支.
4 数 值 模 拟
具有非线性脉冲控制的模型有更加复杂的动力学行为,为了进一步了解非线性脉冲如何影响成功的害虫控制策略,下面从数值上研究模型(1)的动态行为.
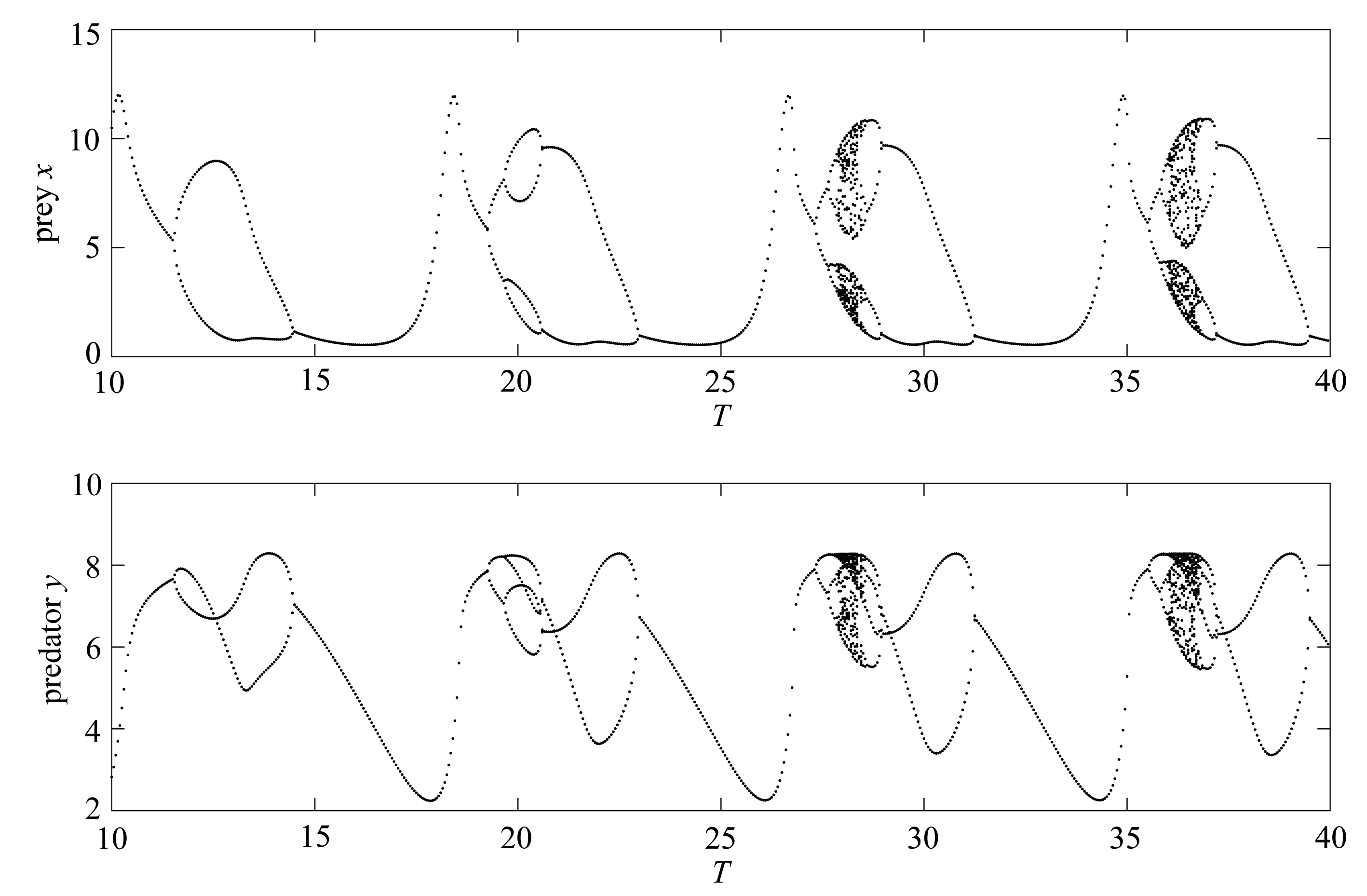
图1 模型(1)周期T的分支参数图
Fig.1 Bifurcation diagrams of model (1) with respect to period T
图1给出了周期参数T为分支参数的分支图(r=2.78,k=16,α=0.65,c=0.37,ω=0.15,D=0.58,δ=0.48,h=0.12,p=0.45),揭示了模型(1)复杂的动态行为,如倍周期分支、周期减半分支、混沌等复杂现象.特别地,当T从10增加到24时,系统由于倍周期分支与周期减半分支使得系统依次出现了周期为1,2,1,2,4,2,1倍T的周期解.当24<T<32时,随着周期T的增加,模型(1)的T周期解失去稳定性,在T=27.32时,出现倍周期分支,随着周期的增大倍周期分支导致混沌现象发生.当周期T进一步增加,系统发生周期减半分支,在T=31.23时系统又一次出现T周期解.有趣的是,当32<T<50时,系统与24<T<32时有完全相同的动力学行为.这种复杂的动态行为说明了害虫控制的困难性以及脉冲周期的重要性.
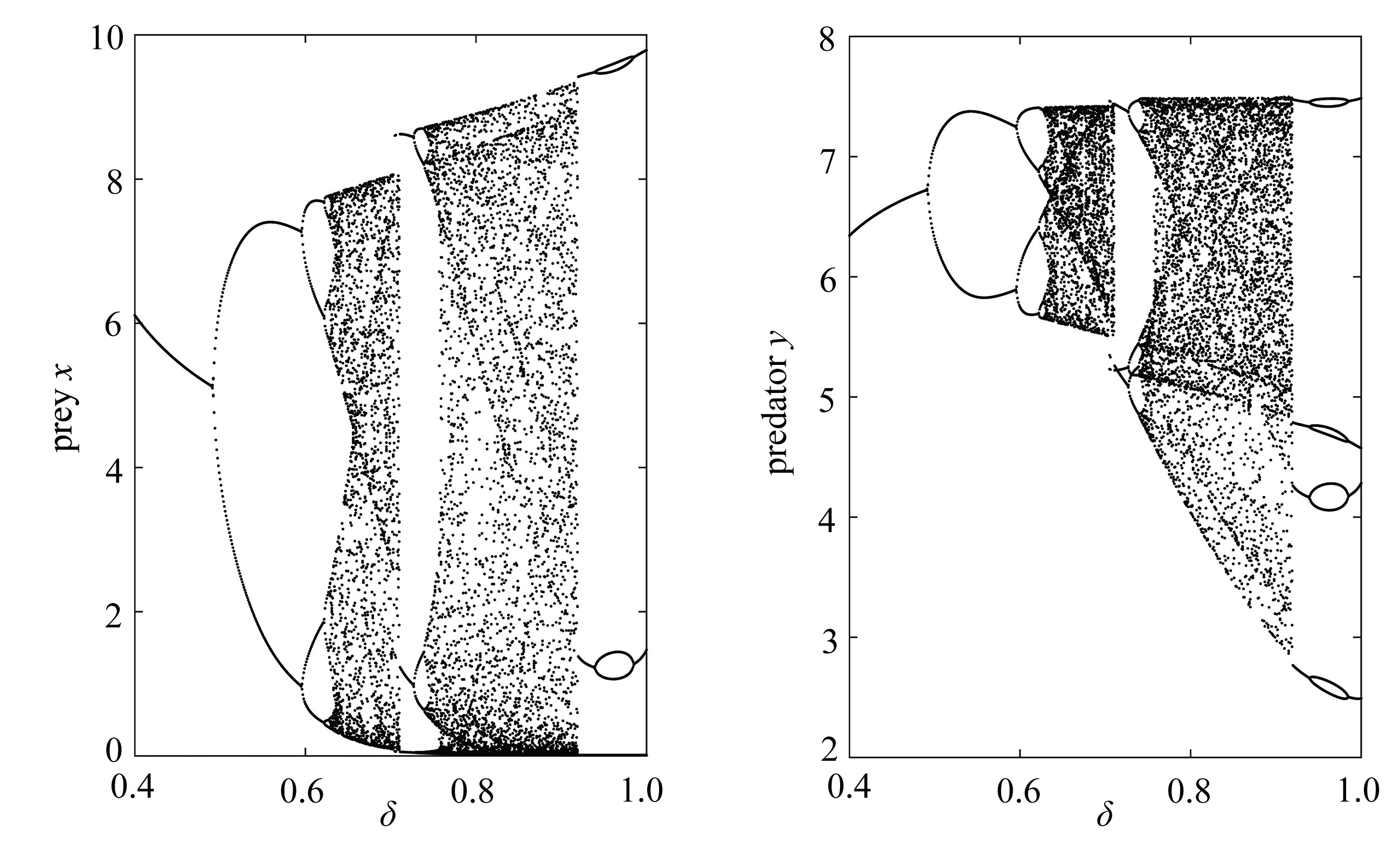
图2 模型(1)最大杀死率δ的分支参数图
Fig.2 Bifurcation diagrams of model (1) with respect to kill rate δ
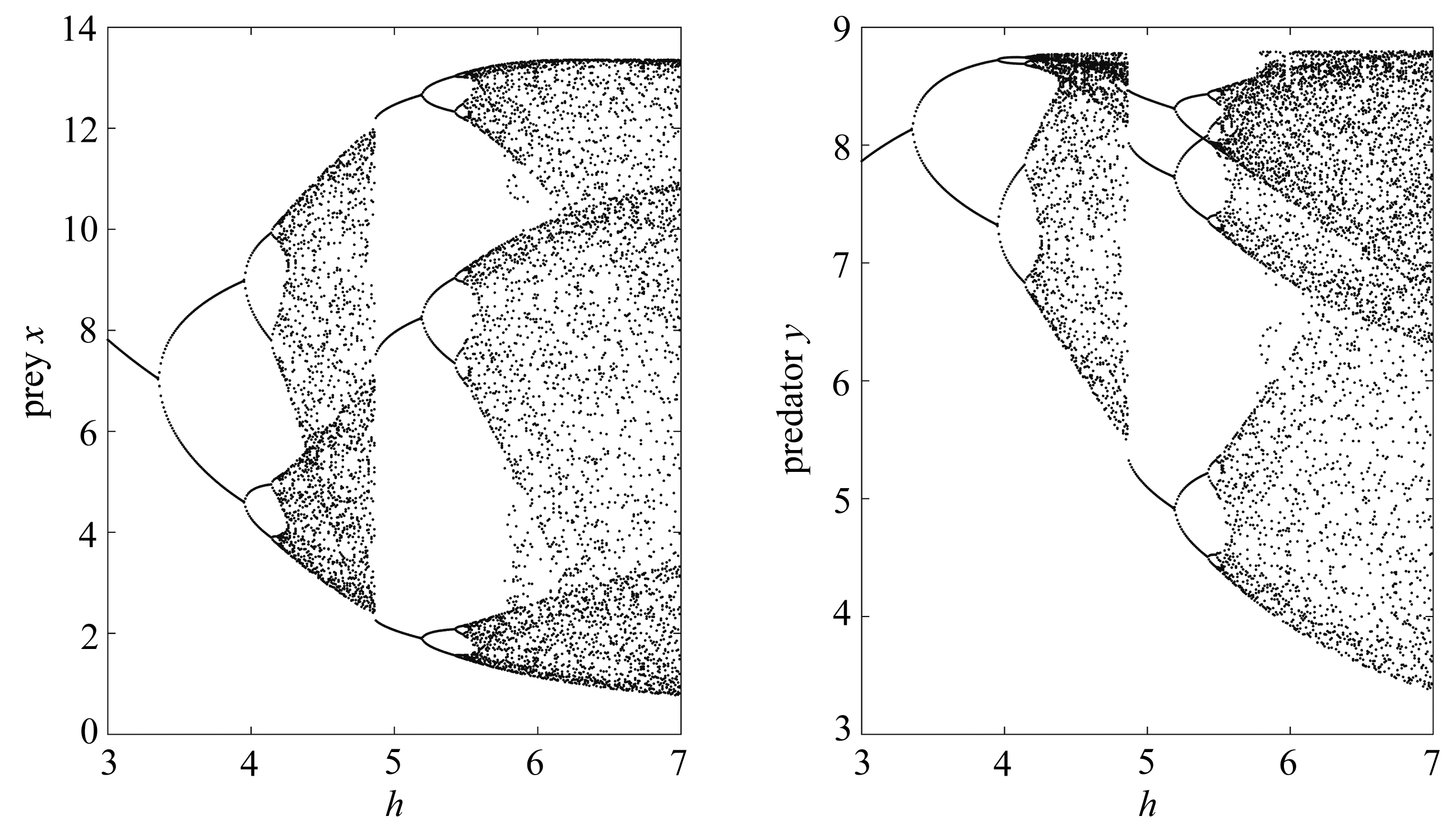
图3 模型(1)参数h的分支参数图
Fig.3 Bifurcation diagrams of model (1) with respect to bifurcation parameter h
为说明资源有限(非线性脉冲)对模型(1)动态行为的影响,图2和图3分别以δ和h为分支参数给出了相应的分支图形,发现系统动力学性质包括倍周期分支、周期减半分支、周期窗口、混沌突变等.图2参数取值为r=2.78,k=16,α=1.2,c=0.37,ω=0.231,D=0.56,h=0.7,p=0.1,T=9;图3参数取值为r=2.78,k=19,α=0.65,c=0.37,ω=0.15,δ=1,D=0.58,p=0.45,T=20.特别地,图3中的数值结果表明随着h的增加,系统的T周期解失去稳定性,在h≈3.5时,系统发生倍周期分支,出现了2T周期解,当参数h进一步增大,倍周期分支导致系统(1)出现混沌现象.当h接近4.87时,混沌忽然消失,进而出现一个3T周期解,随着h继续增大,系统再次发生倍周期分支并最终产生混沌现象.这说明参数h的变化使害虫和天敌种群数量出现不同振幅、不同周期的周期震荡现象.这些结果说明非线性脉冲对模型(1)的动力学行为有显著的影响,也说明具有非线性脉冲的模型具有丰富的动力学行为.
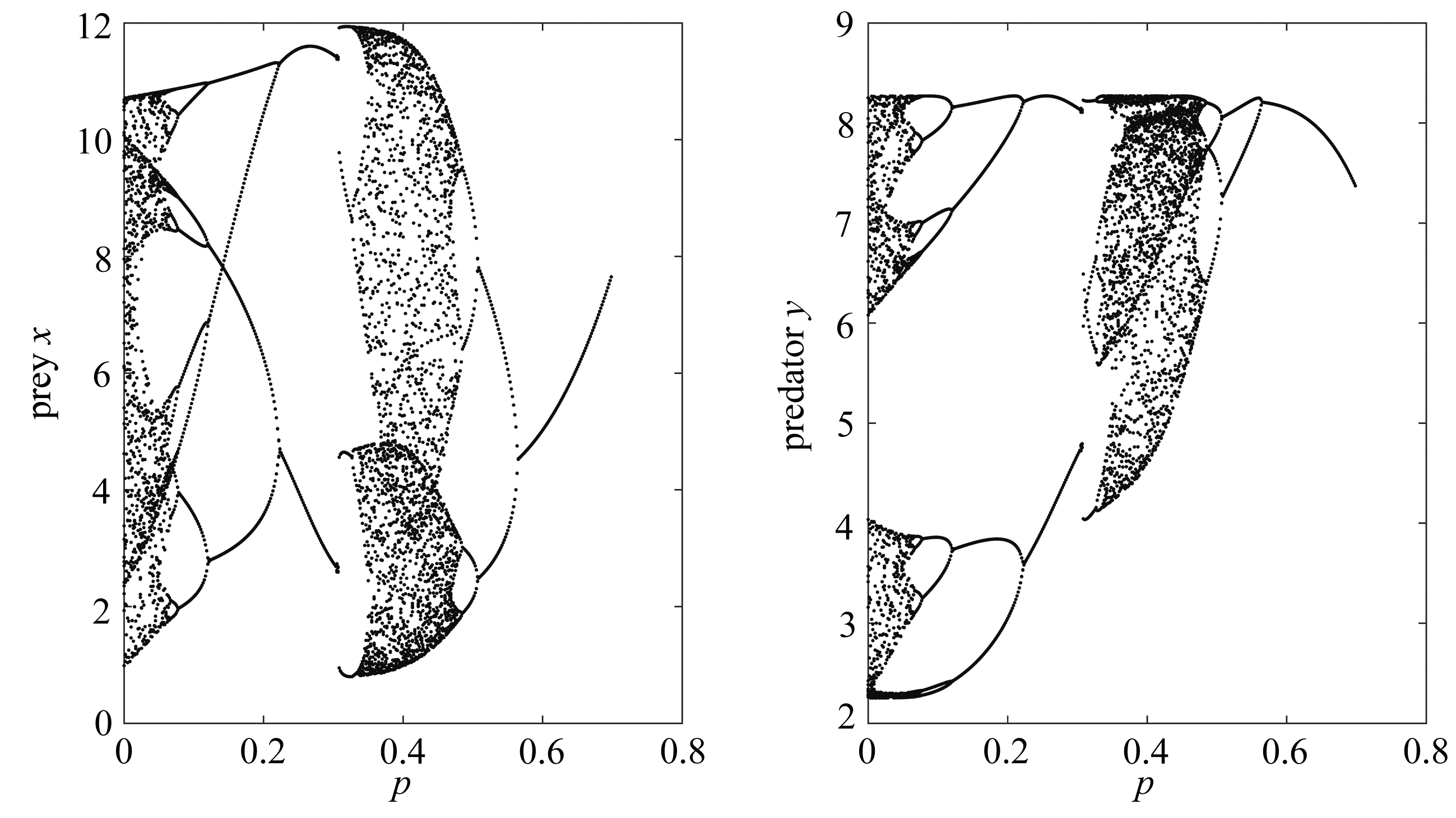
图4 模型(1)参数p的分支参数图
Fig.4 Bifurcation diagrams of model (1) with respect to bifurcation parameter p
图4以杀死率p为分支参数给出了分支图形(r=2.78,k=18,α=0.65,c=0.37,ω=0.15,D=0.58,h=6,T=20),数值模拟表明p由0增加到0.7,模型(1)的动力性质为混沌→周期减半分支→倍周期分支→混沌→周期减半分支,随着p的增加最终回到稳定的T周期解.特别地, 当p=0.305时, 系统出现多个吸引子共存的现象, 即模型(1)出现2T和3T周期解共存现象.
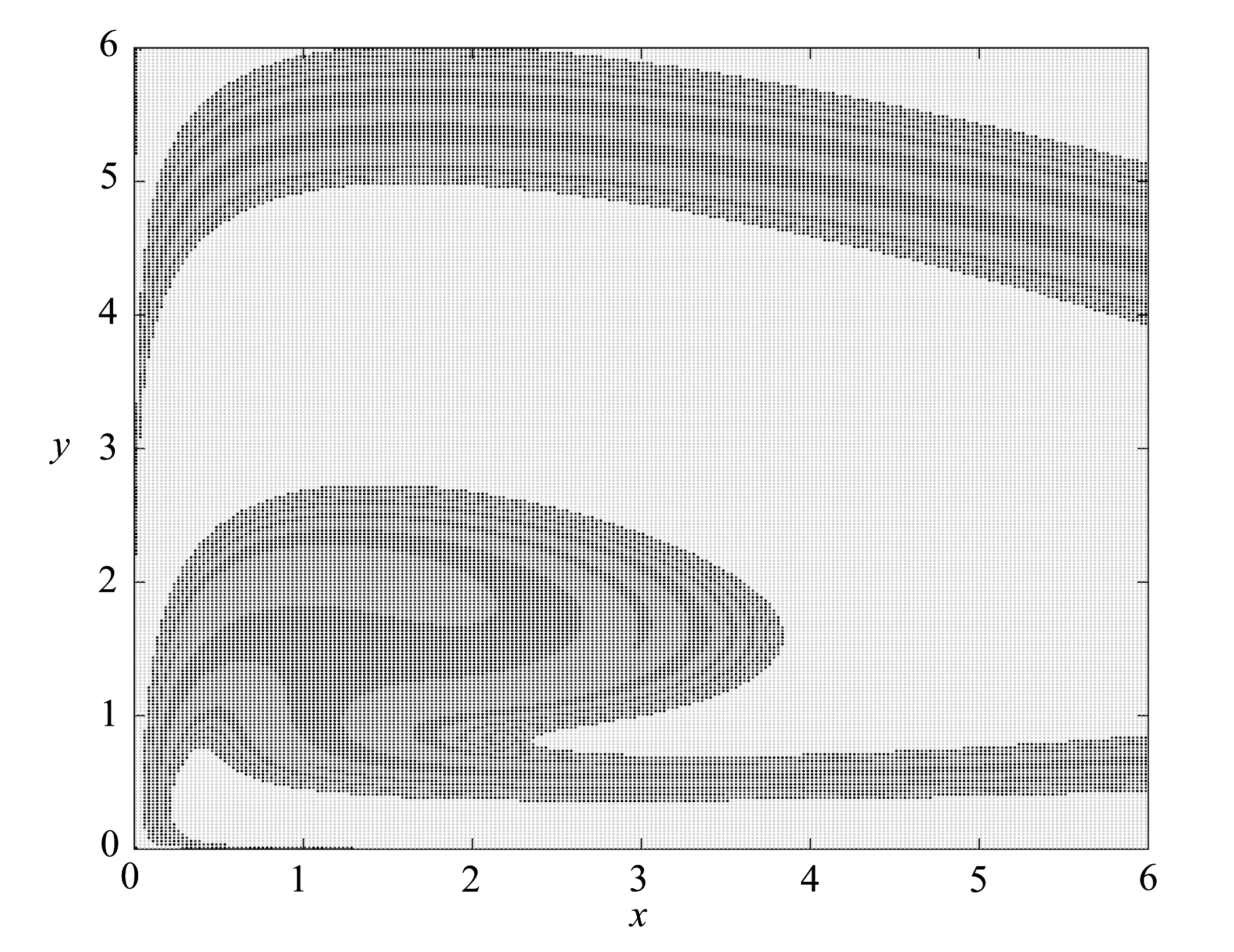
图5 模型(1)的三个吸引子的盆吸引域
Fig.5 The attraction basin of the three attractors of model (1)
为了了解害虫和天敌种群的初始密度如何影响害虫控制策略,从数值上研究模型(1)的共存吸引子,图5给出了系统(1)的三个吸引子的盆吸引域,三种颜色的深浅分别表示系统三个最终稳定的不同吸引子.图5参数取值为r=0.77,k=20,α=0.65,c=0.37,ω=0.15,δ=1,h=2,D=0.38,p=0.32,T=10.5.这证明了当初始条件发生很小的改变时,稳定的吸引子可能会相互切换.如图6所示,若选择初值(x0,y0)=(2,1.2),则模型(1)的解最终状态如图6(a)和(b)所示; 若初值变为(x0,y0)=(3,3.3),则模型(1)的解最终稳定为图6(c)和(d)所示; 当初值变为(x0,y0)=(2,0.5),则模型(1)的解如图6(e)和(f)所示.上述结论验证了害虫和天敌的初始密度对系统最终的状态影响非常明显, 害虫和天敌种群的最终稳定状态还依赖于它们的初始密度, 根据图5和图6, 可以设计合理的控制策略来使害虫或天敌达到预期的吸引子.

图6 模型(1)关于图5的三个共存的吸引子
Fig.6 Three coexistent stable attractors of model (1)
5 结 论
在具有害虫综合控制策略的捕食与被捕食模型中,很多文献的脉冲控制策略都是线性的,而忽略了资源有限作用(非线性脉冲)对害虫控制的影响.在实施控制策略时,应根据害虫和天敌的密度决定释放量的大小,而且受到农业资源有限的影响,因此本文考虑了具有非线性脉冲的捕食与被捕食模型.通过比较定理研究了模型(1)的天敌灭绝周期解的全局稳定性,通过分支理论得到非平凡周期解存在的条件.为了揭示非线性脉冲如何影响成功的害虫控制策略,数值上得到模型(1)存在非常复杂的动力学行为,如倍周期分支、周期减半分支、混沌、吸引子不唯一等.对比参数h和δ的分支图发现,小扰动会使害虫和天敌种群数量出现不同振幅、不同周期的周期震荡现象,即非线性脉冲对模型的动态行为的影响很敏感,进而说明了具有非线性脉冲的捕食与被捕食模型具有更加丰富的动力学性质.图5和图6证明小振幅和大振幅的多吸引子可以共存,从不同初始值出发的解会到达不同振幅的吸引子.实际控制中需要得到振幅小的解,即害虫数量较小的吸引子.这些分支图形揭示了脉冲周期、杀虫剂的剂量、种群的初始密度和数量对成功的控制策略至关重要.本文结论在害虫控制中具有明确的生物含义,对人们合理选择喷洒杀虫剂的时刻、喷洒杀虫剂的剂量等有重要的理论指导意义.
[1] VAN LENTEREN J C.Integrated pest management in protected crops[M]//Integrated Pest Management.DENT D, ed.London: Chapman & Hall, 1995.
[2] LIU B, ZHANG Y J, CHEN L S.The dynamical behaviors of a Lotka-Volterra predator-prey model concerning integrated pest management[J].Nonlinear Analysis Real World Applications, 2005, 6(2): 227-243.
[3] TANG S Y, CHEN L S.Density-dependent birth rate, birth pulses and their population dynamic consequences[J].Journal of Mathematical Biology, 2002, 44(2): 185-199.
[4] TANG S Y, CHEN L S.Multiple attractors in stage-structured population models with birth pulses[J].Bulletin of Mathematical Biology, 2003, 65(3): 479-495.
[5] TANG S Y, CHEN L S.The effect of seasonal harvesting on stage-structured populations models[J].Journal of Mathematical Biology, 2004, 48(4): 357-374.
[6] TANG S Y, XIAO Y N, CHEN L S, et al.Integrated pest management models and their dynamical behavior[J].Bulletin of Mathematical Biology, 2005, 67(1): 115-121.
[7] GAO W, TANG S Y.The effects of impulsive releasing methods of natural enemies on pest control and dynamical complexity[J].Nonlinear Analysis: Hybrid Systems, 2011, 5(3): 540-553.
[8] LI C T, TANG S Y.The effects of timing of pulse spraying and releasing periods on dynamics of generalized predator-prey model[J].International Journal of Biomathematics, 2012, 5(1): 1-27.
[9] TANG S Y, LIANG J H.Global qualitative analysis of a non-smooth Gause predator-prey model with a refuge[J].Nonlinear Analysis, 2013, 76(1): 165-180.
[10] BAEK H K.Qualitative analysis of Beddington-DeAngelis type impulsive predator-prey models[J].Nonlinear Analysis: Real World Applications, 2010, 11: 1312-1322.
[11] 王小娥, 蔺小林, 李建全.一类具有脉冲免疫治疗的HIV-1感染模型的动力学分析[J].应用数学和力学, 2019, 40(7): 728-740.(WANG Xiaoe, LIN Xiaolin, LI Jianquan.Dynamic analysis of a class of HIV-1 infection models with pulsed immunotherapy[J].Applied Mathematics and Mechanics, 2019, 40(7): 728-740.(in Chinese))
[12] 王刚, 唐三一.非线性脉冲状态依赖捕食被捕食模型的定性分析[J].应用数学和力学, 2013, 34(5): 496-505.(WANG Gang, TANG Sanyi.Qualitative analysis of prey-predator model with nonlinear impulsive effects[J].Applied Mathematics and Mechanics, 2013, 34(5): 496-505.(in Chinese))
[13] YANG J, TANG G Y, TANG S Y.Holling type Ⅱ predator-prey model with nonlinear pulse as state-dependent feedback control[J].Journal of Computational and Applied Mathematics, 2016, 291(1): 225-241.
[14] TIAN Y, TANG S Y, CHEKE R A.Dynamic complexity of a predator-prey model for IPM with nonlinear impulsive control incorporating a regulatory factor for predator releases[J].Mathematical Modelling and Analysis, 2019, 24(1): 134-154.
[15] LI C T, TANG S Y.Analyzing a generalized pest-natural enemy model with nonlinear impulsive control[J].Open Mathematics, 2018, 16(1): 1390-1411.
[16] LAKMECHE A, ARINO O.Bifurcation of non-trivial periodic solutions of impulsive differential equations arising chemotherapeutic treatment[J].Dynamics of Continuous, Discrete and Impulsive Systems(Series A): Mathematical Analysis, 2000, 7(2): 265-287.