引 言
同步是一类自然界中广泛存在的群体行为,在生物、物理、化学、工程等多学科领域有非常重要的应用价值,如癫痫病人发病时神经元细胞的同步放电、电力网络中发电机的同步振荡、电子线路上的混沌同步等[1-3].同步一直是近几十年来各领域学者们研究的热点.而作为一种重要的同步方式,相位同步处于研究的中心地位,具有重要的理论研究价值和广阔的应用前景,如能够帮助人们理解癫痫的发病机理、使电网中发电机的振动频率稳定在50~60 Hz,进而提供有效的控制手段[4-13].
在耦合非全同相振子的动力学研究中,人们发现不论系统个体间的拓扑结构为一维规则的链[5-7],还是复杂网络[8],系统整体的同步过程均表现为聚类相位同步.也就是说,随着耦合强度的增加,系统个体通向全局相位同步的路径表现为:具有相近频率或者空间位置临近的振子最容易先形成小的局部同步的集团,再进而吸引频率或者距离相近的振子或同步簇形成更大的簇,直至最终变成全局同步 [5-8].值得注意的是,有关同步的绝大多数研究都是针对这种呈现出分岔树状的聚类相位同步的系统.近期,研究人员发现了另一类新颖的、不同于聚类相位同步的非聚类相位同步[9-11],即系统在达到其临界耦合强度之前,不会出现局部同步簇,而在达到临界耦合强度后,所有的个体则会出现突然间同步的全局同步行为.通过对不同系统同步化过程的研究,结果表明:聚类相位同步出现在耦合的相相关的振子系统中,如Kuramoto相振子或弱随机性的Rossler混沌振子;而非聚类相位同步则广泛出现在耦合的非相相关的振子系统中,如强随机性的Lorenz混沌振子、Lotka-Volterra生态系统、FitzHugh-Nagumo (FHN)神经元系统、Hindmarsh-Rose(HR)神经元系统等[7-8].另外,有研究也指出,系统可以通过将固有的自然频率与空间排布位置二者间的匹配,表现为一类特殊的非聚类相同步 [14].
在众多复杂网络上相同步的研究中,大都是关于分岔树状的聚类相位同步,而同时同步的非聚类相位同步则较少,只在规则网络结构中被报道过,如最近邻耦合的一维规则链[5-7].在更具代表性的复杂网络中,目前研究结果非常少.在工程中,不连续的一阶相变式的分岔会出现从零到大振幅的跳跃,这种行为是危险的.另外,同时同步的相位同步将有助于人们理解自然界中鸟群、鱼群等群体的蜂拥及一致性行为.鉴于此,我们在本文中将进一步针对网络结构为各种复杂网络的更贴合实际的耦合神经元系统开展研究.具体来说,我们将以小世界(WS)网络[15]、无标度(SF)网络[16]以及随机(ER)网络[17]为例,通过对复杂网络结构下噪声激励的耦合FHN系统进行建模与仿真,以数值计算的方式对系统的相位同步路径进行系统研究,并对出现的非聚类相位同步化过程产生的机理做出定性分析解释.
1 耦合FHN系统模型
研究复杂网络上由N个耦合的噪声激励FHN神经元组成的系统,无量纲化的模型为[8]

![]()
i=1,2,…,N,
(1)
其中λ表示系统的耦合强度,(Mij)n×n表示网络的邻接矩阵(如果节点i和节点j之间有连接,则Mij为1,否则为0);N表示节点i的度数,即其连边数总和,用于系统归一化.而ξi(t)代表相互独立的Gauss白噪声,D代表其噪声强度.不失一般性,统一选取参数 =0.01,而激励参数ai通常选取为一个略微大于1的值.由于个体间的差异,不同个体的ai不全相同.考虑到实际的计算,我们将对文中不同复杂网络结构下的耦合FHN系统使用随机选取的同一组参数值.N=100,D=0.2,并随机选取ai∈[1.01,1.21],同时在所有系统计算中保持参数不变.
=0.01,而激励参数ai通常选取为一个略微大于1的值.由于个体间的差异,不同个体的ai不全相同.考虑到实际的计算,我们将对文中不同复杂网络结构下的耦合FHN系统使用随机选取的同一组参数值.N=100,D=0.2,并随机选取ai∈[1.01,1.21],同时在所有系统计算中保持参数不变.
对于带有随机项的随机微分方程,我们将采用二阶段Runge-Kutta法进行数值计算,即在每个时间步长之后再添加一缩放![]() 倍的随机项[18].本文的数值计算中,选取时间步长Δt=0.001,暂态时间1 000,积分时间T=16 000.
倍的随机项[18].本文的数值计算中,选取时间步长Δt=0.001,暂态时间1 000,积分时间T=16 000.
对于网络结构,我们选取了三种有代表性的复杂网络模型:WS网络、SF网络和ER网络.利用生成这些复杂网络结构的标准算法,我们得到100个节点,总边数为250左右的三种网络.具体网络生成过程如下:
WS网络,从由100个节点围成的环出发,每一节点均与其左右最近邻的2个节点相连接,然后以p=0.1的概率将网络中的边随机断开并重新连接,得到边数为200的WS网络.
SF网络, 建立一个5个节点间两两相连的初始网络, 并将每次引入的新节点与3个已有节点相连, 其与第i个已有节点相连接的概率pi与原有节点的个数j以及节点的度ki满足如下关系:
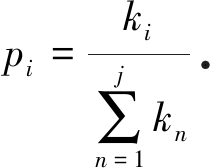
(2)
最终得到一个100个节点的边数为289的SF网络.
ER网络,将100个节点两两连边的概率设为0.05,可生成一个边数为249的ER网络.
2 系统总体特性分析
首先通过对FHN神经元尖峰放电的峰峰间隔间采用线性插值的方法来定义任一时刻FHN神经元的相位[10]:
(3)
其中![]() 表示第i个神经元的第k个尖峰(脉冲放电)的出现时刻.具体地,我们将快变量xi从静息态出发恰好越过阈值0.5的时刻视为其尖峰出现时刻,而每新出现一个尖峰,计数k累加1.根据尖峰放电时刻的相位,通过这种线性内插的方式,就可以给出每一个神经元所有时刻的相位,并用其做进一步的相同步过程分析.
表示第i个神经元的第k个尖峰(脉冲放电)的出现时刻.具体地,我们将快变量xi从静息态出发恰好越过阈值0.5的时刻视为其尖峰出现时刻,而每新出现一个尖峰,计数k累加1.根据尖峰放电时刻的相位,通过这种线性内插的方式,就可以给出每一个神经元所有时刻的相位,并用其做进一步的相同步过程分析.
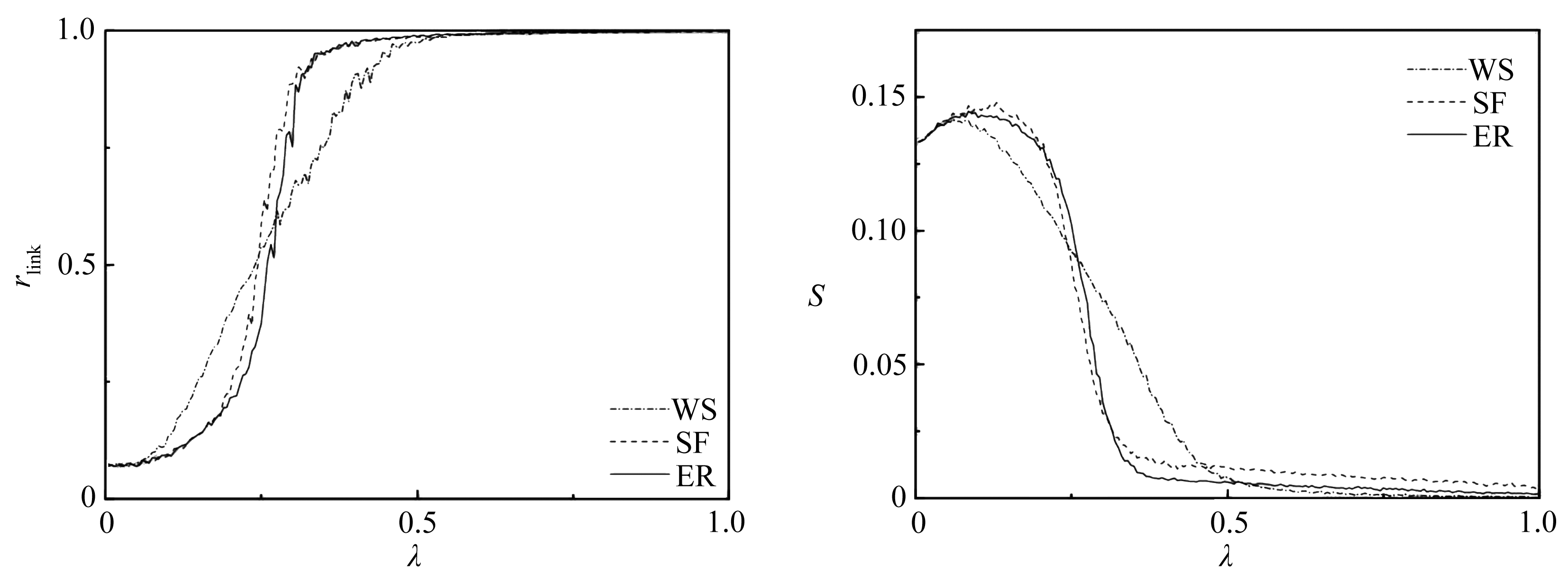
(a) 序参量rlink变化 (b) 标准差S变化
(a) The variation of order parameter rlink (b) The variation of standard deviation S
图1 不同复杂网络下的rlink和S
Fig. 1 Figures of rlink and S for different complex networks
借鉴前人对复杂网络上Kuramoto相振子模型中出现的聚类同步路径的研究,我们定义刻画系统宏观同步模式变化的序参数rlink为[8]
(4)
在实际的数值计算中我们取tr=100,ΔT=800,结果如图1(a)所示.由图可看出,三种网络中系统的序参量rlink随耦合增加均出现快速的上升.这一结果与前人在复杂网络上研究Kuramoto相振子的聚类同步路径一致.在SF网络和ER网络中,耦合强度较弱时(λ≤0.2),神经元个体放电时刻呈现出较强的随机性,rlink很小,系统的同步很弱;而在适度的耦合时(λ≅0.25),rlink急剧地从0.1增加到0.95以上,表明系统个体间从不同步迅速的变为相位一致的很强同步行为.而在WS网络中,当λ∈[0.1,0.45]时,rlink随着λ线性的增加,直至达到系统同步.这些结果表明网络的结构对系统的同步化过程会有很强的影响,SF网络和ER网络由于网络结构的随机性,导致系统呈现出急剧的相同步过程,这也是随机SF网络中网络结构与个体间在一定的匹配关系下能够出现一阶相变的爆炸性同步现象的一个内在原因[2];而WS网络由于结构的规则性,导致系统个体间同步化程度与耦合强度呈正相关关系,变化较为平缓.由此可见,不同复杂网络上会出现同样的动力学行为,但不同的网络结构仍会使系统表现出不同的特性.
定义系统中第i个神经元的平均频率为
(5)
图1(b)中给出了系统平均频率标准差的变化曲线.可以明显地看出,系统平均频率的标准差S随着λ的增加而快速下降,并渐近趋于λc处的零值.与之前类似,在随机SF和ER网络中,S急剧减小;而WS网络中,S在适度的耦合范围内线性地衰减.
3 非聚类相位同步
接下来,我们将具体研究耦合FHN系统在各种典型的复杂网络结构下的同步路径.
图2(a)给出了WS网络下耦合FHN系统中每个神经元的平均放电频率随系统耦合强度的变化.从中可以看出,不同于常见的聚类相位同步,系统在通向全局同步化的过程中,并没有出现任何聚类或成群现象,即我们未观察到任意两个神经元在临界耦合强度之前的任何有限的耦合范围内具有相同频率.另外,还可看出其非聚类相位同步过程可以初略分为2个阶段:首先是神经元的频率增强阶段,在这一阶段中,所有神经元的平均频率逐渐增加直至达到峰值;之后是频率衰减阶段,在这一阶段中,所有个体的平均频率逐渐下降并趋于一致,且在临界耦合强度λc处所有神经元个体转变为同步状态.在完成了这一过程之后,随着耦合强度的进一步增强,个体的平均频率会进一步下降并表现出长尾效应.所有这些行为都非常类似于之前对于规则链上耦合FHN神经元系统的研究[9-10].在图2(b)中,我们给出了其对应的网络拓扑结构,以近邻和次近邻,以及一些长程的连边为其主要特征.
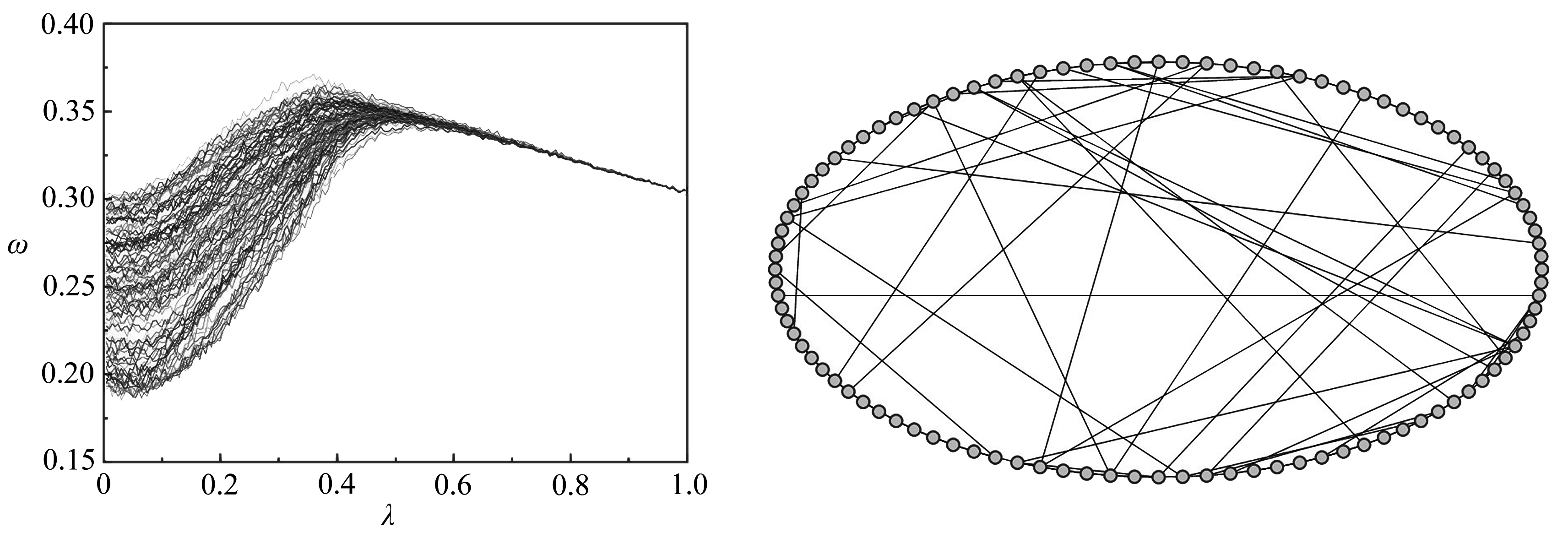
(a) 神经元的平均频率ω (b) WS网络结构
(a) Average frequency ω of the neuron (b) The WS network structure
图2 WS网络下耦合FHN系统的平均频率和网络结构
Fig. 2 The average frequency and the network structure of the coupled FHN system for the WS network
另外通过对随机SF和ER网络上的耦合FHN系统进行研究,我们发现结果依然表现出与WS网络上的耦合FHN系统相同的规律.相应的结果分别在图3和图4中给出.从图中可进一步看出,由于网络结构的不同,个体频率的增强和衰减过程都表现出一些细微的差异.
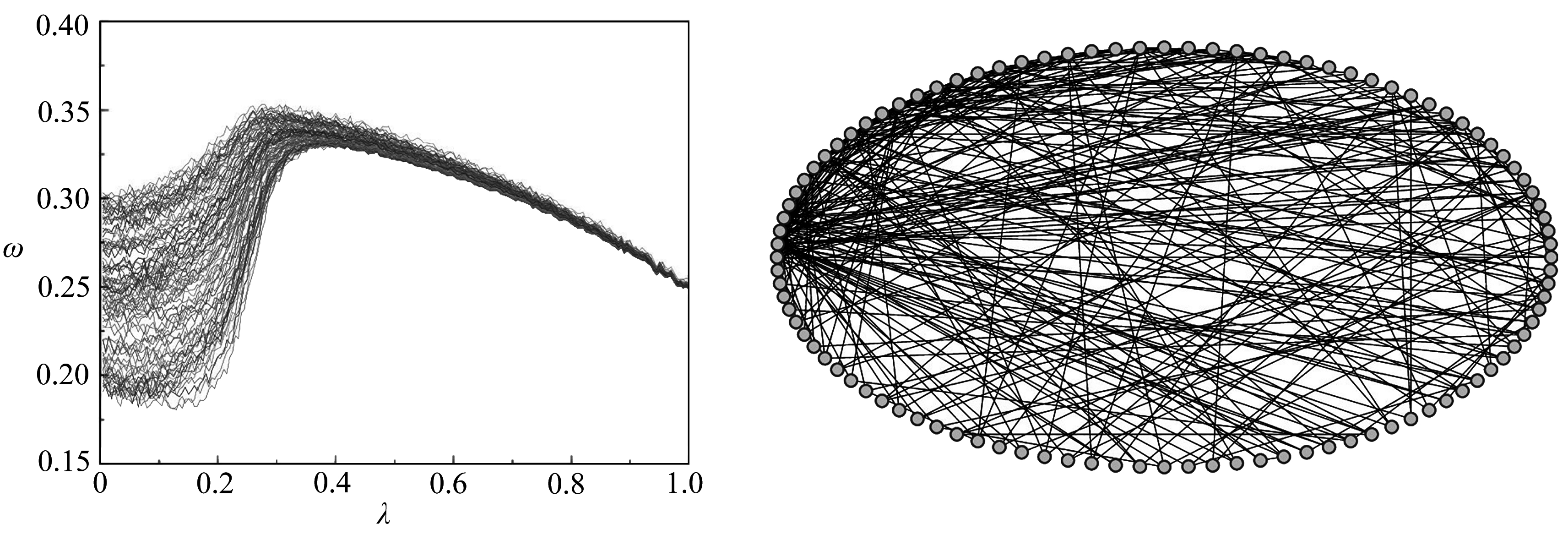
(a) 神经元的平均频率ω (b) SF网络结构
(a) Average frequency ω of the neuron (b) The SF network structure
图3 SF网络下耦合FHN系统的平均频率和网络结构
Fig. 3 The average frequency and the network structure of the coupled FHN system for the SF network
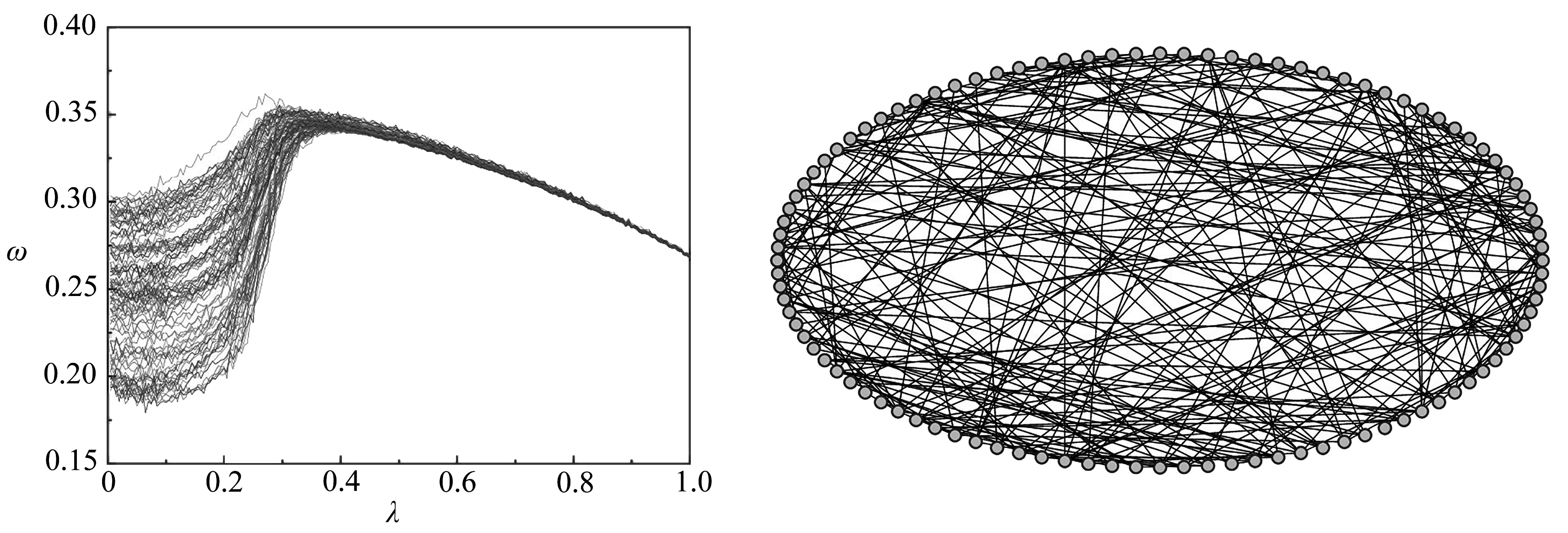
(a) 神经元的平均频率ω (b) ER网络结构
(a) Average frequency ω of the neuron (b) The ER network structure
图4 ER网络下耦合FHN系统的平均频率和网络结构
Fig. 4 The average frequency and the network structure of the coupled FHN system for the ER network
4 机 理 分 析
以下对系统中频率增加和频率衰减的行为做进一步的机理分析.我们将以WS网络下的耦合FHN系统为例.
4.1 频率增加
不失一般性,任意选取图2(a)频率增加区间中的一个耦合强度,如λ=0.25,选择第1个神经元及与其相关联的一些神经元.图5中绘制了xi的时序图.可以发现,对于这5个神经元,除了图中首尾两端的两个完全同步峰(大致在t=28.5和t=39.5处)和一个部分同步峰(大致在t=32.5处)外,一些神经元的放电尖峰由于耦合作用将对其相连的其他神经元产生激励作用,如x3的第2个尖峰(大致在t=31.5处)使其他神经元的值出现小幅度的增加.类似的现象可以非常普遍地观察到.正是由于耦合神经元间的相互作用,新插入的尖峰逐渐增加,将进而导致所有神经元放电频率的不断上升.并且随着耦合强度的增强,尖峰插入的数量也会不断增加,直至神经元的平均频率达到峰值.
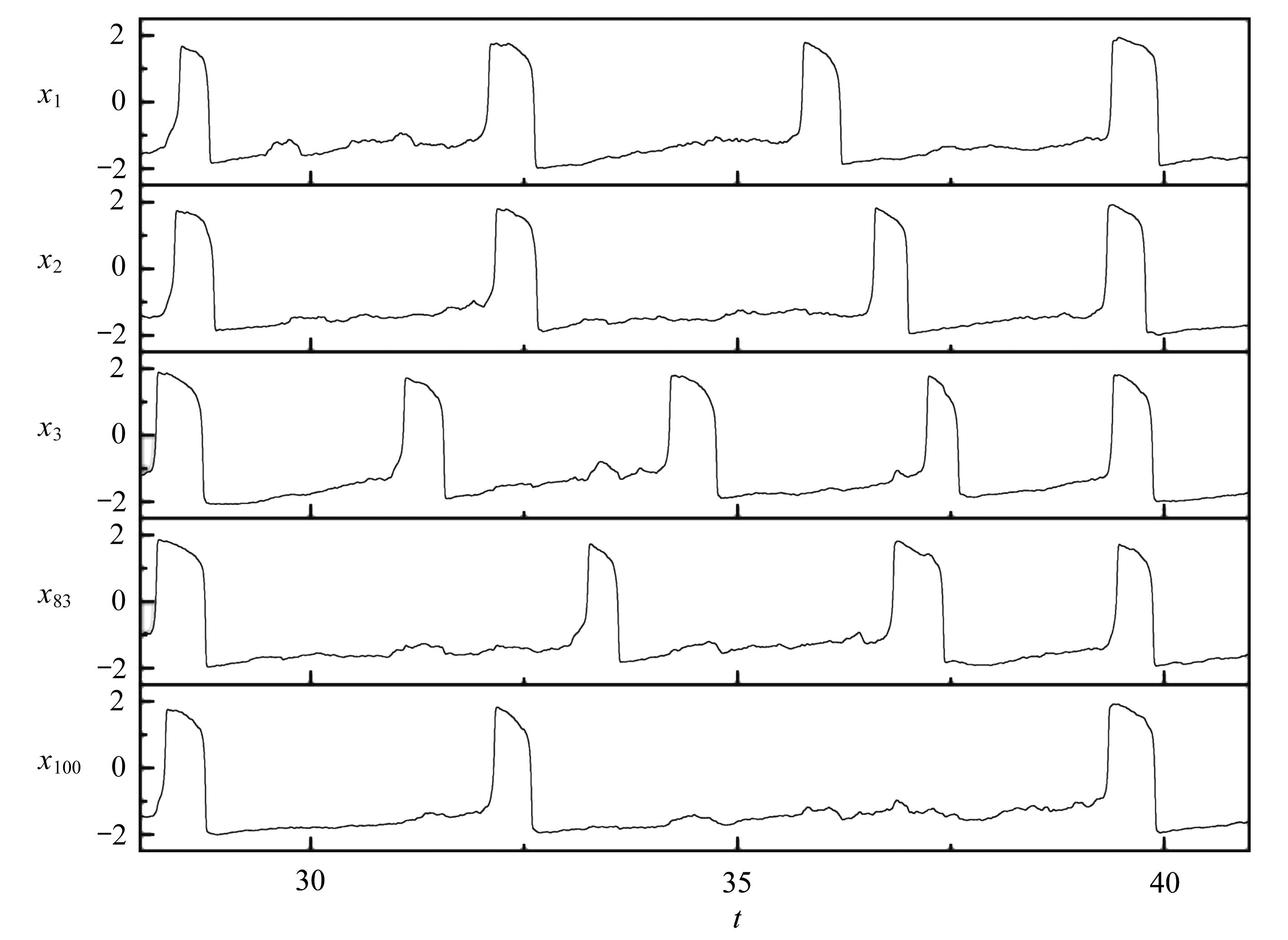
图5 耦合强度为0.25的x-t曲线
Fig. 5 Evolution of x-t curves for 5 connected neurons, λ=0.25
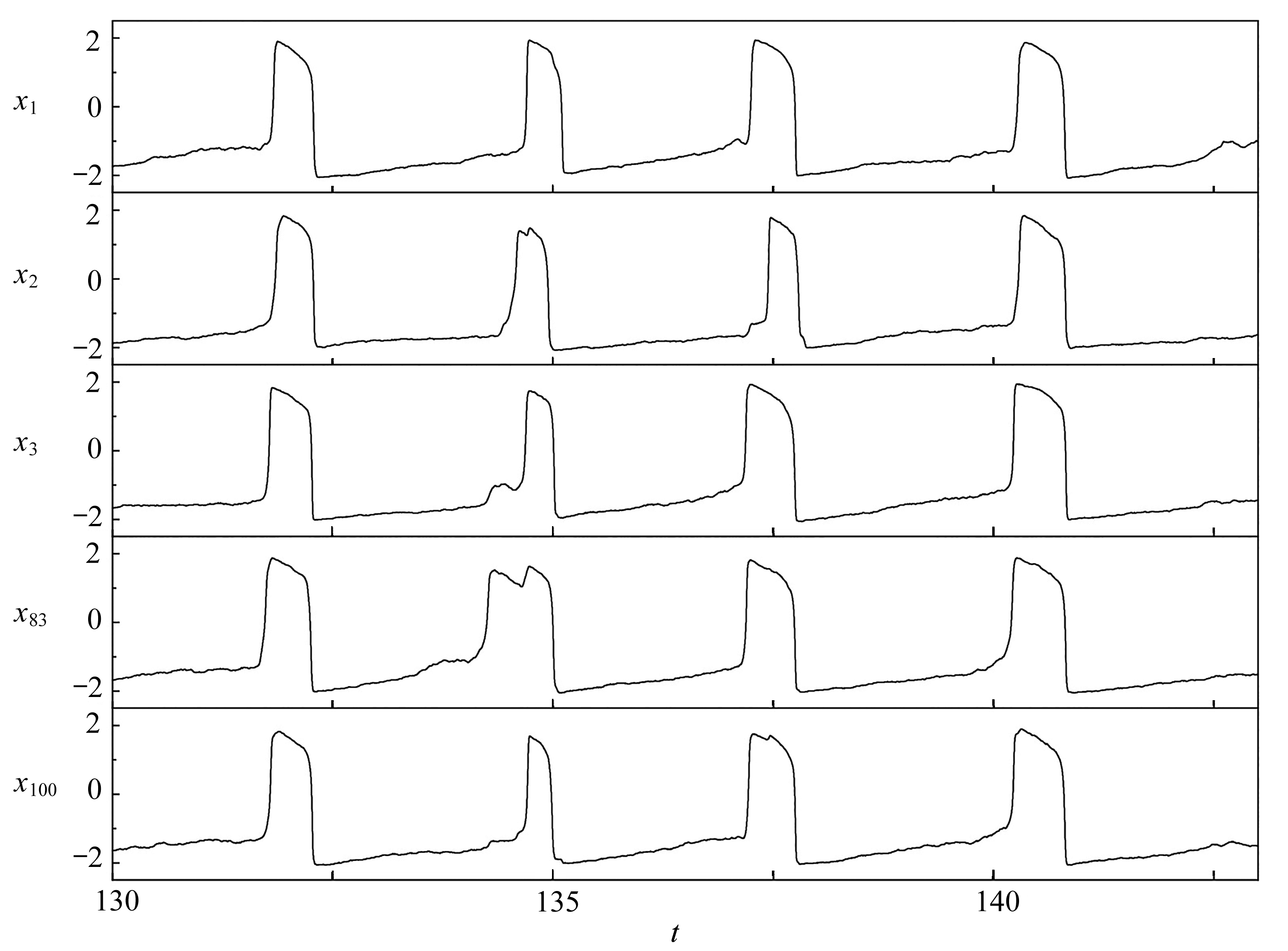
图6 耦合强度为0.55的x-t曲线
Fig. 6 Evolution of x-t curves for 5 connected neurons, λ=0.55
4.2 频率衰减
不失一般性,选取λ=0.55这一处于频率衰减阶段的耦合强度下系统的动力学来观察,在图6中选择同样的5个神经元绘制xi的时序图.结果发现,除了4个大致相同的同步峰(大致在t=132,t=135,t=137.5和t=140.5处)外,部分神经元个体尖峰的宽度明显大于正常宽度(非常显著的是处于t=134和t=135之间的x83),其来源于两个相邻尖峰之间的弥合.由此,我们可以看出,系统中的两个原本分离的尖峰由于耦合相互作用将逐渐弥合,变成一个尖峰,而这显然将导致频率的逐渐衰减.随着耦合强度的增加,这种效应逐渐体现,系统将逐渐趋于同步,并且所有神经元平均频率将变小,结果正如我们在图2(a)中所看到的.
5 结果与讨论
本文主要以复杂网络上的耦合FHN神经元模型为对象,研究了其上的非聚类相同步现象,并得出以下结论:
1) 与规则网络下耦合神经系统的非聚类同步路径类似,系统在复杂网络下仍然呈现出非聚类相位同步现象,即平均频率随着耦合强度λ的增加而表现为先增强后衰减,并在临界耦合λc处达到全局同步.而在同步化过程中,始终没有聚类相同步现象发生.
2) 通过对rlink和S的曲线分析,发现在复杂网络下,它们几乎都单调变化,这一点非常类似于耦合相振子中的聚类相同步.但网络结构随机性的强弱导致系统的同步化过程急剧或缓慢变化,随机性越强,系统越容易达到同步.
3) 通过对不同λ值下相连接神经元xi时序图的分析,我们发现,神经元的频率增强是由相关个体的新尖峰插入导致的,而系统的频率衰减则是由神经元的相邻尖峰之间逐渐弥合产生的.
4) 由于在非聚类相同步发展过程中,频率增强和频率衰减是由对应尖峰的插入和相邻尖峰的弥合造成的,其本质上完全不同于通常的耦合相振子的聚类同步现象,即不同自然频率的相振子逐渐改变自身旋转频率,与其自然频率相近或者距离相近的振子先实现相同步,产生成群现象,并进而集团逐渐扩大实现系统的全局相同步.由此可见,本文中的非聚类相同步有着完全不同的物理路径.
5) 最后,我们希望,本文针对耦合神经元系统中一般化同步过程的研究能够激起非线性科学和计算神经科学方面的研究人员的普遍兴趣.
致谢 本文作者衷心感谢占萌教授对本文的大力帮助和修改建议.
[1] ARENAS A, D AZ-GUILERA A, KURTHS J, et al. Synchronization in complex networks[J]. Physics Reports, 2008, 469(3): 93-153.
AZ-GUILERA A, KURTHS J, et al. Synchronization in complex networks[J]. Physics Reports, 2008, 469(3): 93-153.
[2] TANG Y, QIAN F, GAO H, et al. Synchronization in complex networks and its application: a survey of recent advances and challenges[J]. Annual Reviews in Control, 2014, 38(2): 184-198.
[3] PECORA L M, CARROLL T L, JOHNSON G A, et al. Fundamentals of synchronization in chaotic systems, concepts, and applications[J]. Chaos, 1997, 7(4): 520-543.
[4] ROSENBLUM M G, PIKOVSKY A S, KURTHS J. Phase synchronization of chaotic oscillators[J]. Physical Review Letters, 1996, 76(11): 1804-1807.
[5] ZHENG Z G, HU G, HU B B. Phase slips and phase synchronization of coupled oscillators[J]. Physical Review Letters, 1998, 81(24): 5318-5321.
[6] 郑志刚, 胡岗, 周昌松, 等. 耦合混沌系统的相同步: 从高维混沌到低维混沌[J]. 物理学报, 2000, 49(12): 2320-2327.(ZHENG Zhigang, HU Gang, ZHOU Changsong, et al. Phase synchronization in coupled chaotic systems: transitions from high-to low-dimensional chaos[J]. Acta Physica Sinica, 2000, 49(12): 2320-2327.(in Chinese))
[7] ZHAN M, ZHENG Z G, HU G, et al. Nonlocal chaotic phase synchronization[J]. Physical Review E, 2000, 62(3): 3552-3557.
[8] GOMEZ-GARDENES J, MORENO Y, ARENAS A. Paths to synchronization on complex networks[J]. Physical Review Letters, 2007, 98(3): 034101. DOI: 10.1103/PhysRevLett.98.034101.
[9] CHIANG W Y, LAI P Y, CHAN C K. Frequency enhancement in coupled noisy excitable elements[J]. Physical Review Letters, 2011, 106(25): 254102. DOI: 10.1103/PhysRevLett.106.254102.
[10] LIU S, ZHAN M. Clustering versus non-clustering phases synchronizations[J]. Chaos, 2014, 24(1): 013104. DOI: 10.1063/1.4861685.
[11] LIU S, HE Z W, ZHAN M. Firing rates of coupled noisy excitable elements[J]. Frontiers of Physics, 2014, 9(1): 120-127.
[12] 张玮玮, 陈定元, 吴然超, 等. 一类基于忆阻器分数阶时滞神经网络的修正投影同步[J]. 应用数学和力学, 2018, 39(2): 239-248.(ZHANG Weiwei, CHEN Dingyuan, WU Ranchao, et al. Modified-projective-synchronization of memristor-based fractional-order delayed neural networks[J]. Applied Mathematics and Mechanics, 2018, 39(2): 239-248.(in Chinese))
[13] 李天择, 郭明, 陈向勇, 等. 基于多切换传输的复变量混沌系统的有限时组合同步控制[J]. 应用数学和力学, 2019, 40(11): 1299-1308.(LI Tianze, GUO Ming, CHEN Xiangyong, et al. Finite-time combination synchronization control of complex-variable chaotic systems with multi-switching transmission[J]. Applied Mathematics and Mechanics, 2019, 40(11): 1299-1308.(in Chinese))
[14] HUANG Z, ZHAN M, LI F, et al. Single-clustering synchronization in a ring of Kuramoto oscillators[J]. Journal of Physics A: Mathematical and Theoretical, 2014, 47(12): 125101. DOI: 10.1088/1751-8113/47/12/125101.
[15] WATTS D J ,STROGATZ S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440-442.
[16] BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.
[17] STROGATZ S H. Exploring complex networks[J]. Nature, 2001, 410(6825): 268-276.
[18] HONEYCUTT R L. Stochastic Runge-Kutta algorithms, Ⅰ: white noise[J]. Physical Review A, 1992, 45(2): 600-603.