引 言
压电材料具有良好的机电耦合效应,在结构监测、精密定位和航空航天等领域已广泛应用[1].由于压电材料的脆性,在加工、制造和使用过程中会产生各种缺陷(如裂纹、位错和孔洞).因此,对于压电材料中含复杂缺陷断裂行为的研究具有重要意义,此方面的工作已取得了丰硕的成果[2-4].准晶体作为20世纪80年代发现的一种新型材料[5-7],坚硬且富有弹性、有非常高的电阻率和相当低的热传导系数等,其应用前景广泛.研究表明,准晶材料也具有压电效应[8].压电准晶材料是考虑压电效应的准晶材料,从理论上被Rao等[9]和Altay等[10]提出并深入研究,由于其良好的特性,有望成为智能结构中的传感器和执行器.所以对其断裂理论的研究刻不容缓,而且自提出以来,许多学者已经做了大量的研究工作[11-18].
孔边应力分布问题的研究可追溯到19世纪末[19],对于各类材料中此类问题的研究从未间断[20-21],尤其是孔边切口或裂纹的应力分布问题也是具有实际意义的热点问题[22-25].近年来,许多学者也研究了准晶或压电准晶中孔边切口或裂纹问题.利用复变函数方法和保角映射技术,Yang和Li等[26-27]研究了一维六方压电准晶中圆孔边含三条裂纹和周期裂纹的反平面问题.Yu等[28]用复变函数结合Stroh公式研究了一维六方压电准晶体中椭圆孔的应力集中问题,给出了场的解析表达式.采用Stroh公式,樊世旺等[29]研究了一维六方压电准晶三角形孔边裂纹的反平面问题.白巧梅等[30]研究了一维六方压电准晶中正六边形孔边裂纹的反平面问题.Guo等[31]研究了一维六方准晶中椭圆孔含有4条裂纹的解析解问题.
但是,我们注意到,针对压电准晶材料中孔边切口或裂纹的研究相对较少,且大多研究都针对比较单一的模型,局限于少数孔口形状,如圆形、椭圆形、正三角形、规则四边形等,没有能够提供一般性的求解方法.本文针对压电准晶体中孔边裂纹问题进行了研究,利用复变函数方法和SC变换[25]技术,构造了新的映射函数,将物理平面上正n边形孔边裂纹外部区域映射到像平面的单位圆内部.应用Cauchy 积分公式,得到了裂纹尖端处声子场应力、相位子场应力和电位移强度因子的解析解,并给出了随着孔洞尺寸和裂纹长度的变化对场强度因子的影响规律,这与文献[29-30]得到的相关结果一致.与前述结果相比,本文结果更具有一般性,结合SC变换的复变函数方法,理论上适用任意正多边形孔口含裂纹的情形,因此该方法也具有普适性,从而为工程力学、材料的制备和应用等提供了良好的理论依据.
1 一维六方压电准晶基本方程
以原点为中心,建立直角坐标系,令x3方向为一维六方压电准晶的准周期方向,平面x1Ox2为周期平面.当一维六方压电准晶中的缺陷沿x3方向穿透时,材料的几何性质将不随准周期方向改变.此时,相应的弹性问题可以分解为各向同性晶体的平面应变问题[32],和声子场与相位子场耦合的反平面问题[7].本文考虑反平面问题,则考虑压电效应下一维六方准晶在x1Ox2平面内的基本方程如下:
本构方程
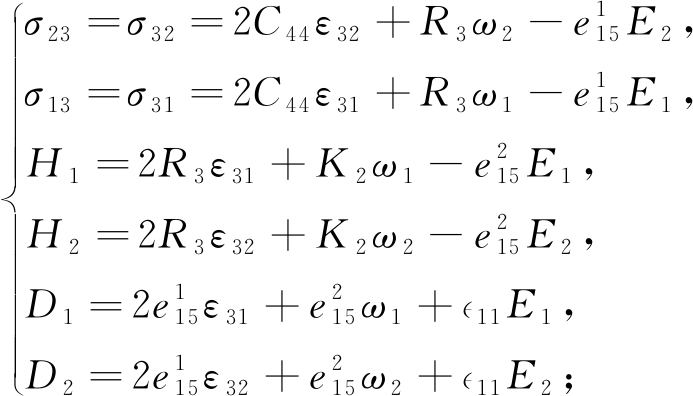
(1)
平衡方程

(2)
几何方程
(3)
式(1)~(3)中,∂ju3=∂u3/∂xj,σij,εij和u3分别为声子场的应力、应变和位移分量;Hj,ωj和ω分别为相位子场的应力、应变和位移分量;Dj和Ej分别为电位移和电场分量;φ表示电势;C44和K2分别为声子场和相位子场弹性常数;R3是声子场和相位子场耦合的独立弹性常数;![]() 为压电常数;
为压电常数;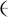 11为介电常数.
11为介电常数.
由式(1)~(3)得控制方程:
A 2U=0,
2U=0,
(4)
其中![]() 是Laplace算子,以及
是Laplace算子,以及

(5)
因为A≠0,则式(4)可写为
 2u3=0,
2u3=0, 2ω=0,
2ω=0, 2φ=0.
2φ=0.
(6)
根据复变函数理论可知[33],式(6)可以转化为求解3个调和函数, 将u3,ω,φ分别表示为3个解析函数的实部,则
u3=Reφ1(z),ω=Reφ2(z),φ=Reφ3(z),
(7)
其中![]() 是3个待求解的解析函数,Re表示实部.
是3个待求解的解析函数,Re表示实部.
根据解析函数的性质和Cauchy-Riemann方程,由式(1)、(3)和(7)得
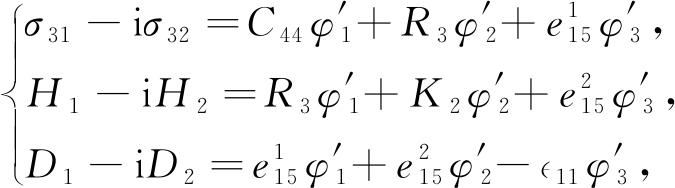
(8)
其中
对于任意复函数g(t),有![]() 其中
其中![]() 表示复数的共轭, 则式(8)可写为
表示复数的共轭, 则式(8)可写为
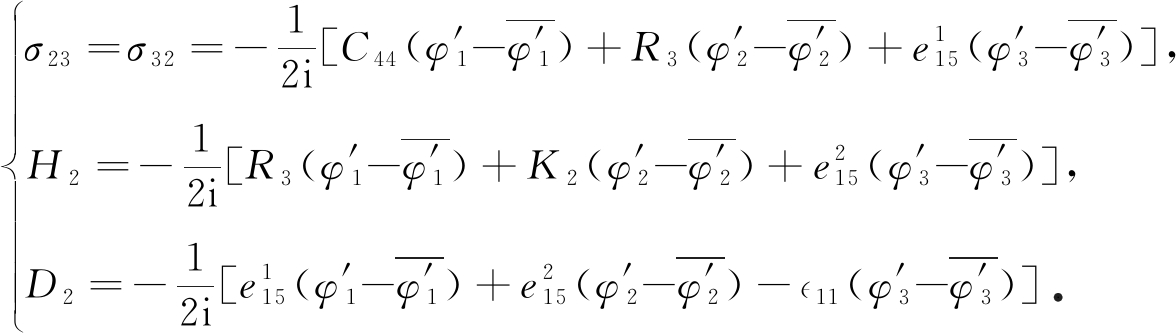
(9)
在给定边界和初始条件下可以求出φi,则进一步可以确定应力场和电位移场.
2 正n边形孔边裂纹问题
在无限大一维六方压电准晶中包含一裂纹的正n边形孔口,孔口的边长为a,沿x1方向有长度为L的裂纹,并沿准周期方向穿透.如图1所示,给出了正十边形含裂纹的模型.假设压电准晶体在无穷远处受到沿准周期方向的纵向剪切应力τ,以及面内电载荷D0的作用.
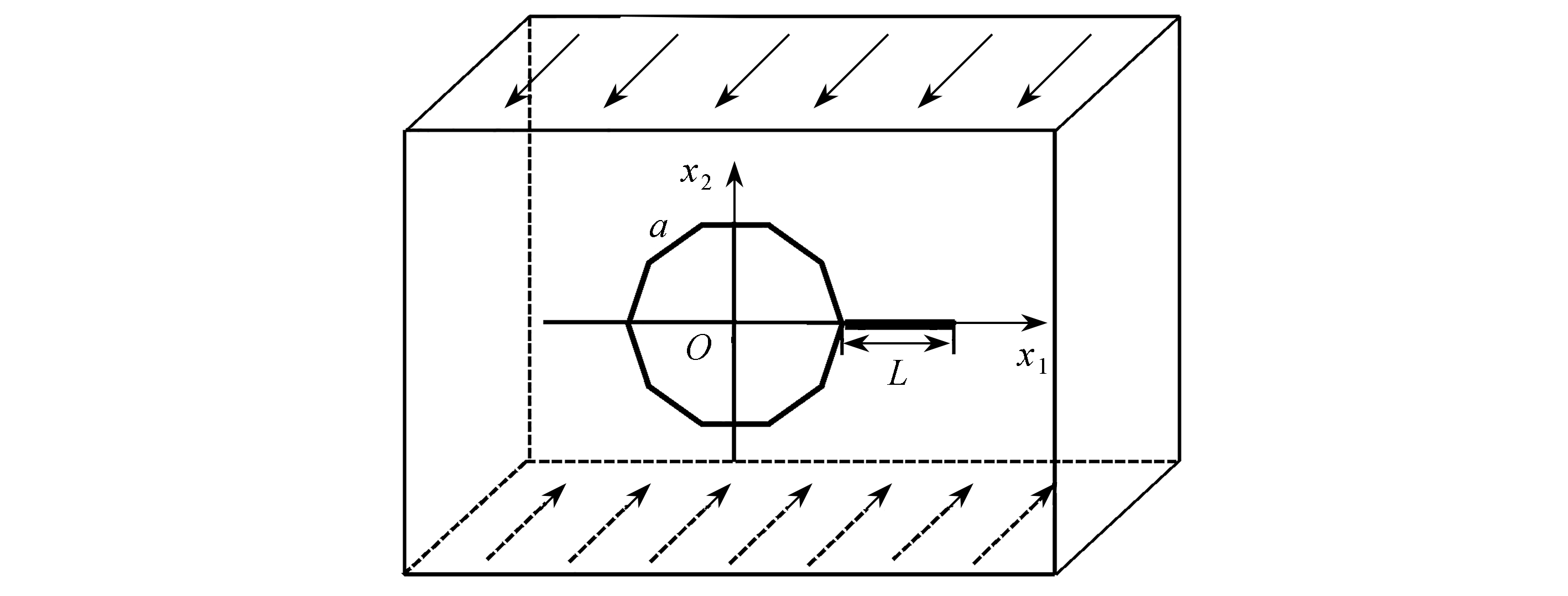
图1 无限大一维六方压电准晶中带裂纹的正十边形孔口
Fig. 1 The regular decagon hole with a crack in an infinite 1D hexagonal quasicrystal
由线弹性理论可知,此问题可以转化为压电准晶体在无穷远处不受力,只在正n边形孔口及裂纹面上受到纵向剪应力和电载荷的作用:σ32=-τ1,H2=-τ2,D2=-D0.本文主要研究构造保形映射方法的有效性,所以仅考虑电不可导通边界条件,可写为
(10)
其中N表示孔口裂纹的边界.将式(9)代入式(10)得
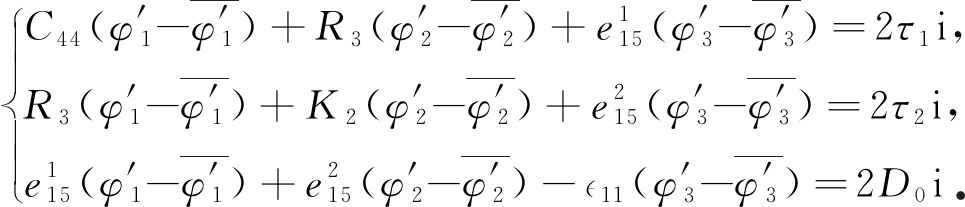
(11)
为了将z平面上正n边形孔外部区域映射到z1平面单位圆的外部区域,下面给出SC变换的映射函数:
(12)
其中, 常数R和C1分别为正n边形的形状系数和位置系数.将z1平面上的无穷远点变换为z平面的无穷远点,则C1=0.这里n表示正n边形的边数,aj是与正n边形对应的顶点,αj(j=1,2,…,n)表示外角除以π的实常数,则
将aj和αj代入式(12)中,得到正n边形外部区域到单位圆孔外部区域的映射函数,将式(12)展开成级数形式[34],有
(13)
其中
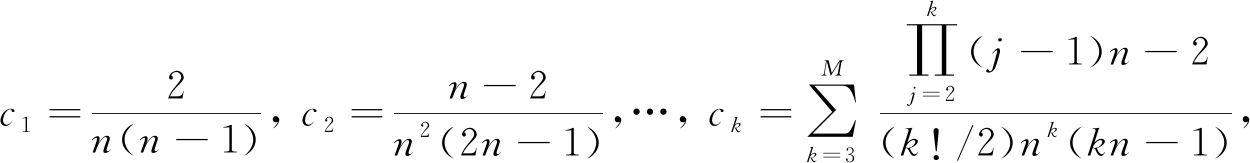
这里R是与a的平方长度相关的常数.
当n分别为3,4,6时,代入式(13)所得变换分别与文献[29-30,35]所得变换一致.
为了便于求解,将含有裂纹圆的外部变换到圆的内部,则得到图1所示正n边形孔外部区域保角映射到单位圆内部的复合保形映射.图2给出了保角映射的简要过程,这里z1平面上圆的边界及裂纹的上岸和下岸变换到ζ平面上圆的部分边界.
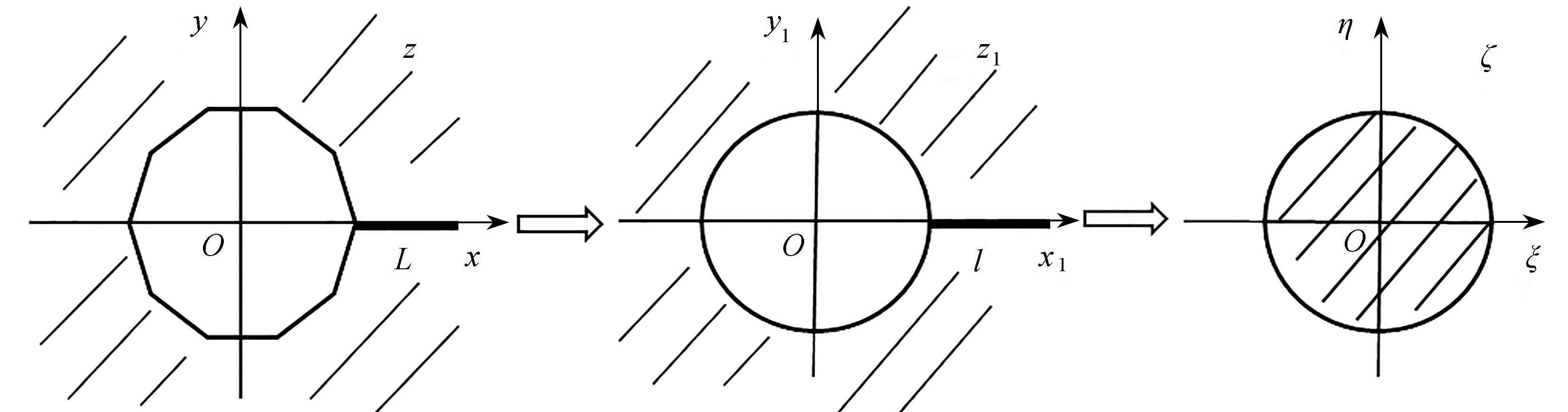
图2 保角映射原理图
Fig. 2 Schematic diagram of the conformal mapping
由式(12)和(13)得复合保形映射为
z=ω(ζ)=R(μ(ζ)+c1μ1-n(ζ)+c2μ1-2n(ζ)+…+ckμ1-kn(ζ)),
(14)
其中μ(ζ)是将圆孔及裂纹外部区域变换到单位圆内部的映射函数[36]:
2(ε+1)(1-ζ2)2)1/2},
(15)
这里ε为一实参数,记为
(16)
式中l为z1平面的裂纹长度.可由点的对应关系得到
d+L=R[(1+l)+c1(1+l)1-n+c2(1+l)1-2n+…+ck(1+l)1-kn],
(17)
这里d为正n边形中心到顶点的距离,由对应关系,有z1=d+L=ω(1).令
ψi(ζ)=φi(z)=φi(ω(ζ)), i=1,2,3,
则有
(18)
将式(18)代入式(11),对单位圆上任一点ζ=σ=eiθ,有

(19)
这里已令![]()
记ζ为单位圆内任意一点,将式(19)两端同乘以(dσ/(σ-ζ))/(2πi),沿边界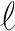 积分,由Cauchy积分公式得
积分,由Cauchy积分公式得
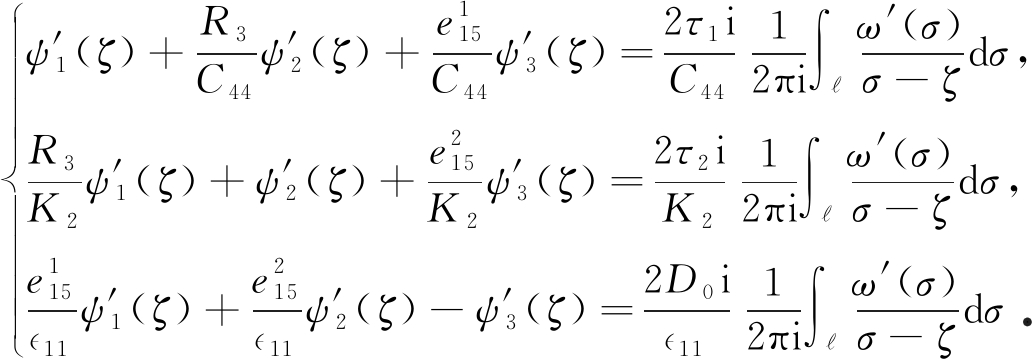
(20)
对方程(14)关于ζ求微分,得
ω′(ζ)=Rμ′(ζ)[1+c1(1-n)μ-n(ζ)+c2(1-2n)μ-2n(ζ)+…+
ck(1-kn)μ-kn(ζ)],
(21)
其中
μ′(ζ)=
利用复变函数和留数定理,得出式(20)右端的积分为
(22)
将式(22)代入式(20),再利用式(18)得
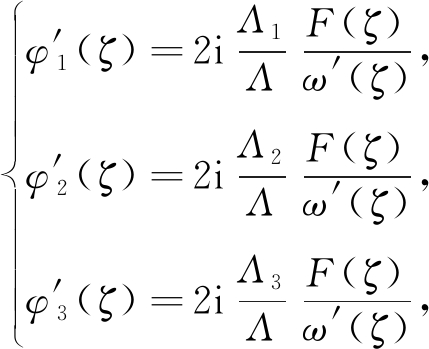
(23)
其中
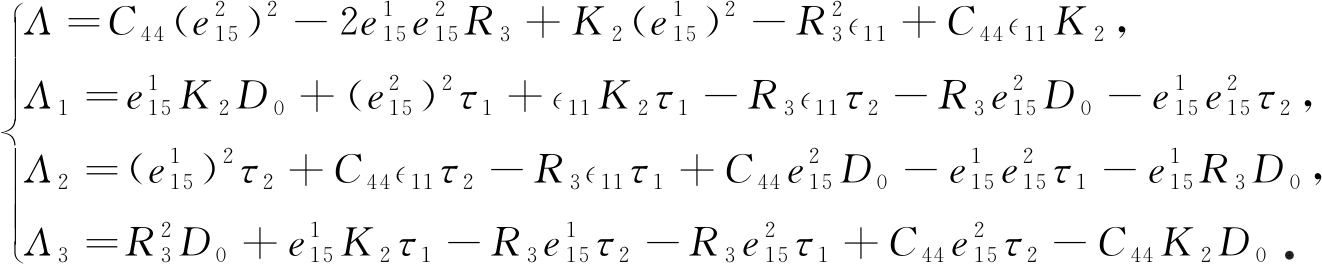
再将式(23)代入式(9)得到z平面内各场的表达式.
3 场强度因子
在电不可导通边界条件下,由文献[7]可知,在z平面内裂纹尖端z=d+L处,对应ζ平面内ζ=1处声子场、相位子场应力和电位移强度因子分别为
(24)
这里
(25)
以及
ω′(1)=Rμ′(1)[1+c1(1-n)μ-n(1)+c2(1-2n)μ-2n(1)+…+
ck(1-kn)μ-kn(1)],
(26)
(27)
将式(25)~(27)代入式(24)得正n边形孔边裂纹尖端附近的场强度因子:
(28)
其中
ω″(1)=Rμ″(1)[1+c1(1-n)μ-n(1)+c2(1-2n)μ-2n(1)+…+
ck(1-kn)μ-kn(1)],
(29)
(30)
再将场强度因子无量纲化,式(28)除以![]() 得到正n边形孔边裂纹尖端等效场强度因子:
得到正n边形孔边裂纹尖端等效场强度因子:
(31)
其中L′=(h+L)/2.当n为奇数时,h为正n边形的高; 当n为偶数时,h为正n边形两顶点之间的最大距离.
于是式(28)简化为
(32)
其中K见式(31).
为了便于工程应用,针对几个特殊的情形n=3,4,5,6,给出等效强度因子K的具体表达式.为此引入记号![]() 则计算结果如下.
则计算结果如下.
当n=3时,式(31)退化为一维六方压电准晶含正三角形孔边裂纹的等效场强度因子:
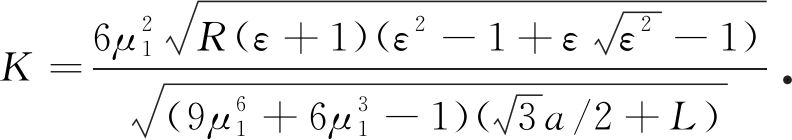
(33)
这与文献[29]所得结果一致.
当n=4时,式(31)退化为一维六方压电准晶含正方形孔边裂纹的等效场强度因子:
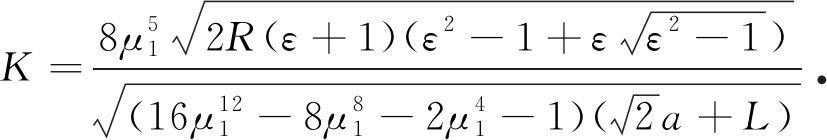
(34)
当n=5时,式(31)退化为一维六方压电准晶含正五边形孔边裂纹的等效场强度因子:
(35)
当n=6时,式(31)退化为一维六方压电准晶含正六边形孔边裂纹的等效场强度因子:
(36)
4 数值算例和分析
当n=3时,即退化为一维六方压电准晶中正三角形孔边裂纹的反平面问题.此时,等效场强度因子K可用于确定正三角形孔边裂纹的场强度因子.由式(30)可知,等效场强度因子与正三角形的边长和裂纹长度有关.引入无量纲参数L/a(裂纹长度和边长之比)来表征裂纹尺寸,下面的数值计算可以更加直观地看出几何参数对等效场强度因子的影响规律.
图3给出了当a=0.03,0.04,0.05 m时,等效场强度因子K随裂纹长度L/a的变化关系曲线,可以看出,等效场强度因子K的值随着裂纹长度L/a的增大而增大,然后趋于定值,说明正三角形裂纹尺寸对等效场强度因子影响较小.图4给出了当L/a=0.01,0.05,0.10时,等效场强度因子K随孔洞边长a的变化关系曲线,结果显示等效场强度因子K的值随着孔洞边长a的增大而增大,具有明显增长趋势,说明孔洞的尺寸对等效场强度因子K的影响特别显著,很容易使材料产生损坏.这与文献[29]的结果一致.
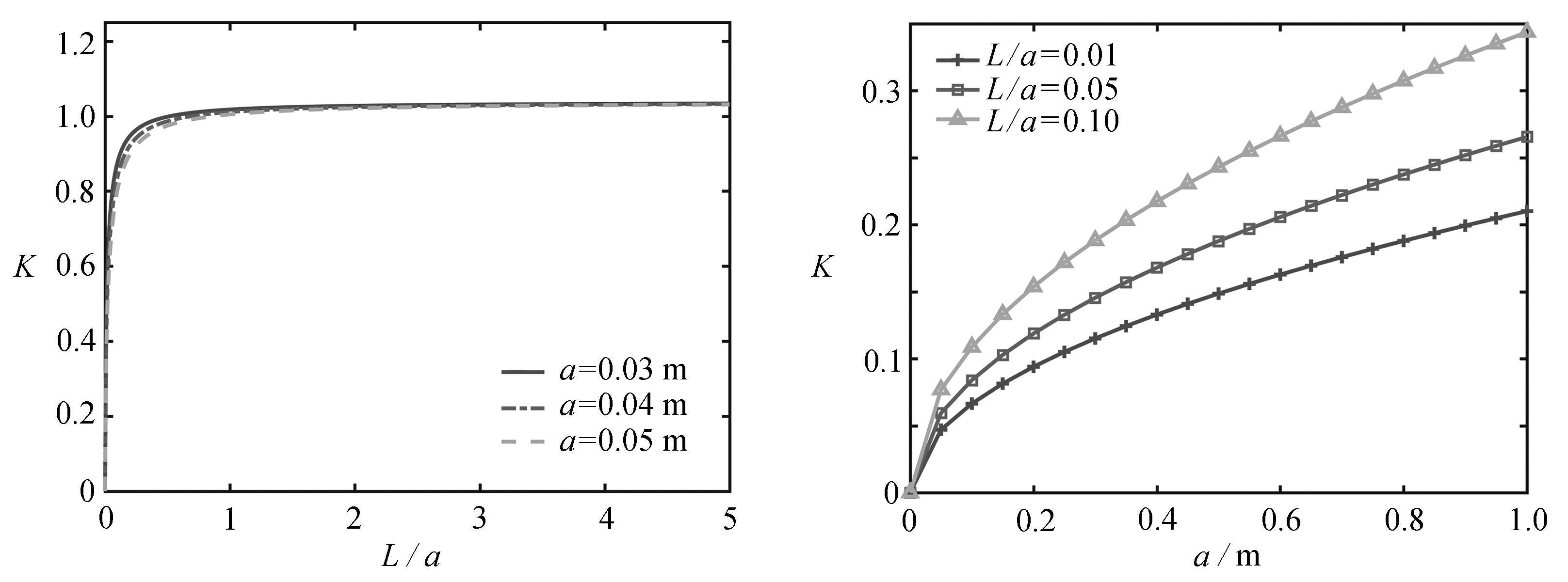
图3 等效场强度因子K随L/a的变化关系 图4 等效场强度因子K随a的变化关系
Fig. 3 Variation ofKwithL/a Fig. 4 Variation ofKwitha
当n=5时,即退化为一维六方压电准晶中正五形孔边裂纹的反平面问题.
图5和图6分别给出了等效场强度因子K随裂纹长度和孔洞边长的变化关系.可以看出,等效场强度因子K的值随着裂纹长度L/a的增大而增大,然后趋于一个稳定的常数,表明裂纹扩展到一定程度后对等效场强度因子影响很小; 等效场强度因子K的值随着孔洞边长a的增大而增大,增长趋势明显,说明孔洞的尺寸对等效场强度因子K的影响特别显著,很容易使材料产生损坏.
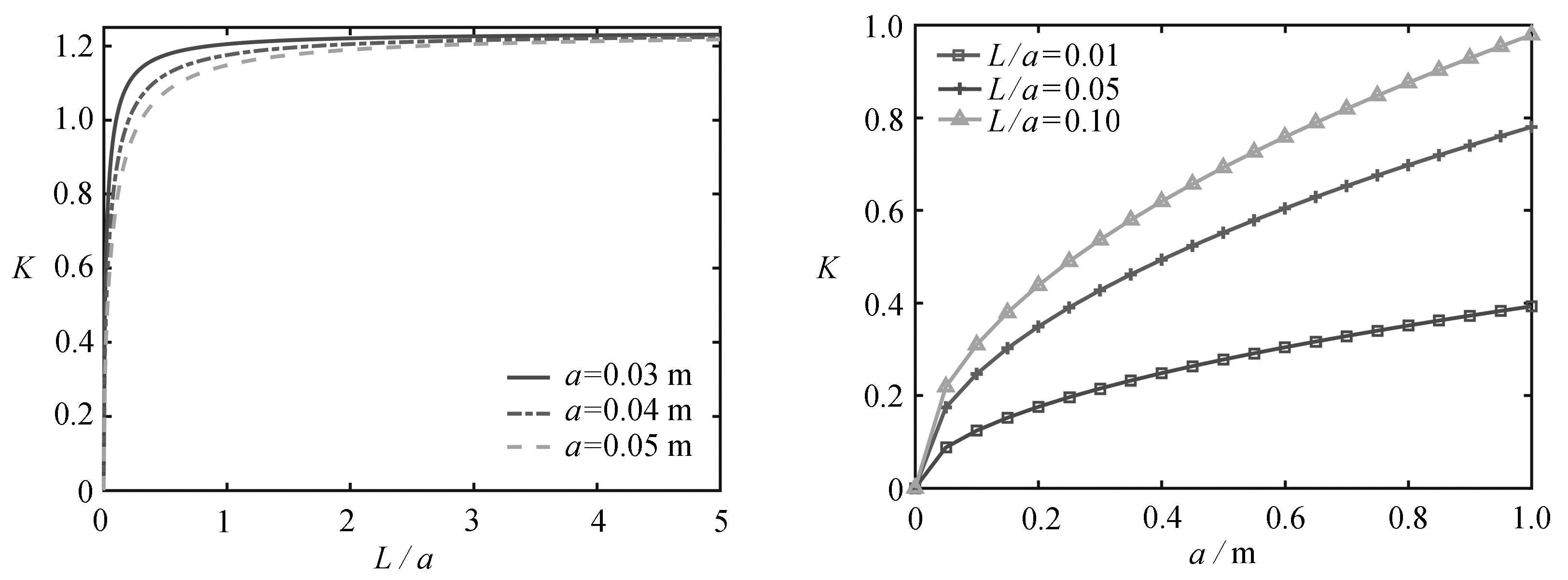
图5 等效场强度因子K随L/a的变化关系 图6 等效场强度因子K随a的变化关系
Fig. 5 Variation ofKwithL/a Fig. 6 Variation ofKwitha
当n=6时,即退化为一维六方压电准晶中正六边形孔边裂纹的反平面问题.图7给出了当a=0.03,0.04,0.05 m时,等效场强度因子K随裂纹长度L/a的变化关系曲线,可以看出,等效场强度因子K的值随着裂纹长度L/a的增大而增大,然后逐渐趋于平稳.图8给出了当L/a=0.01,0.05,0.10时,等效场强度因子K随边长a的变化关系曲线,显示出等效场强度因子K的值随着边长a的增大而增大,上升趋势明显,说明孔洞的尺寸对等效场强度因子K的影响特别显著,很容易使材料产生损坏.这与文献[30]的结果一致.
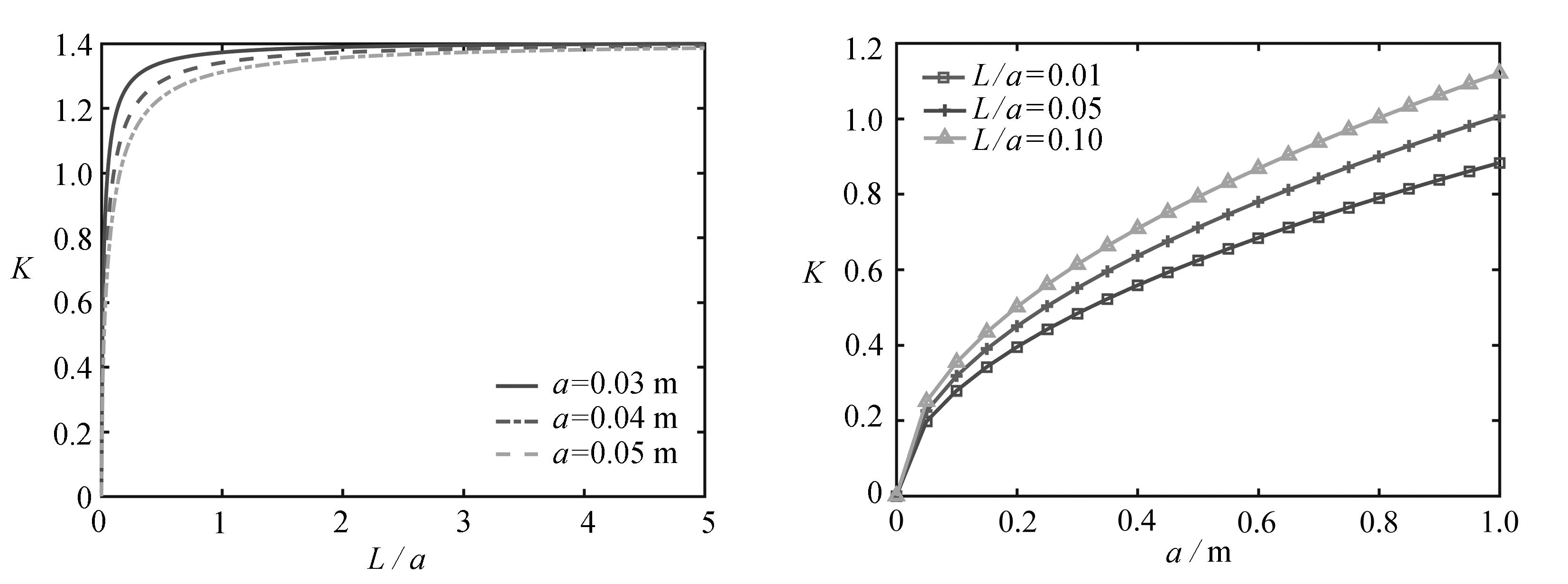
图7 等效场强度因子K随L/a的变化关系 图8 等效场强度因子K随a的变化关系
Fig. 7 Variation ofKwithL/a Fig. 8 Variation ofKwitha
5 结 论
本文在电不可导通边界条件下,利用复变函数方法和SC变换技术,构造了新的映射函数,研究了在无限大一维六方压电准晶中正n边形孔边裂纹的反平面问题.应用Cauchy积分公式,给出了裂纹尖端处声子场应力、相位子场应力和电位移强度因子的解析解.数值结果也表明,等效场强度因子K的值随着裂纹长度L/a的增大而增大,然后逐渐趋于平稳.等效场强度因子K的值随着孔洞边长a的增大而增大,而且增长趋势明显,说明孔洞的尺寸对等效场强度因子K的影响特别显著,很容易使材料产生损坏.这与文献[29-30]的相关结果一致,从而为工程材料的制备和应用提供了良好的理论依据.
[1] VALDOVINOS J. Pediatric mechanical circulatory support applications for frequency-leveraged piezoelectric hydraulic pumps[D]. PhD Thesis. Los Angeles: University of California, 2014.
[2] WANG Y J, GAO C F. The mode Ⅲ cracks originating from the edge of a circular hole in a piezoelectric solid[J].International Journal of Solids and Structures, 2008,45(16): 4590-4599.
[3] WANG Y J, GAO C F, SONG H. The anti-plane solution for the edge cracks originating from an arbitrary hole in a piezoelectric material[J].Mechanics Research Communications, 2015,65: 17-23.
[4] GHERROUS M, FERDJANI H. Analysis of a Griffith crack at the interface of two piezoelectric materials under anti-plane loading[J].Continuum Mechanics and Thermodynamics, 2016,28(6): 1683-1704.
[5] SHECHTMAN D G, BLECH I A, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J].Physical Review Letters, 1984,53(20): 1951-1953.
[6] LI L H, FAN T Y. Exact solutions of two semi-infinite collinear cracks in a strip of one dimensional hexagonal quasicrystal[J].Applied Mathematics and Computation, 2008,196(1): 1-5.
[7] FAN T Y.Mathematical Theory of Elasticity of Quasicrystals and Its Applications[M]. Berlin: Springer, 2011.
[8] HU C Z, WANG R H, DING D H, et al. Piezoelectric effects in quasicrystals[J].Physical Review B, 1997,56(5): 2463-2468.
[9] RAO K R M, RAO P H, CHAITANYA B S K. Piezoelectricity in quasicrystals: a group-theoretical study[J].Pramana:Journal of Physics, 2007,68(3): 481-487.
[10] ALTAY G, DÖKMECI M C. On the fundamental equations of piezoelasticity of quasicrystal media[J].International Journal of Solids and Structures, 2012,49(23/24): 3255-3262.
[11] LI X Y, LI P D, WU T H, et al. Three-dimensional fundamental solutions for one-dimensional hexagonal quasicrystal with piezoelectric effect[J].Physics Letters A, 2014,378(10): 826-834.
[12] ZHANG L L, ZHANG Y M, GAO Y. General solutions of plane elasticity of one-dimensional orthorhombic quasicrystals with piezoelectric effect[J].Physics Letters A, 2014,378(37): 2768-2776.
[13] GUO J H, PAN E. Three-phase cylinder model of 1D hexagonal piezoelectric quasicrystal composites[J].Journal of Applied Mechanics, 2016,83(8): 081007.
[14] YU J, GUO J H, PAN E, et al. General solutions of plane problem in one-dimensional quasicrystal piezoelectric materials and its application on fracture mechanics[J].Applied Mathematics and Mechanics(English Edition), 2015,36(6): 793-814.
[15] FAN T Y, LI X F, SUN Y F. A moving screw dislocation in a one-dimensional hexagonal quasicrystals[J].Acta Physica Sinica(Overseas Edition), 1999,8(4): 288-295.
[16] LI X, HUO H S, SHI P P. Analytic solutions of two collinear fast propagating cracks in a symmetrical strip of one-dimensional hexagonal piezoelectric quasicrystals[J].Chinese Journal of Solid Mechanics, 2014,35(2): 1-7.
[17] TUPHOLME G E. A non-uniformly loaded anti-plane crack embedded in a half-space of a one-dimensional piezoelectric quasicrystal[J].Meccanica, 2018,53(4/5): 973-983.
[18] ZHOU Y B, LI X F. Two collinear mode-Ⅲ cracks in one-dimensional hexagonal piezoelectric quasicrystal strip[J].Engineering Fracture Mechanics, 2018,189: 133-147.
[19] KIRSCH G. Die theorie der elastizität und die bedürfnisse der festigkeitslehre[J].Zantralblatt Verlin Deutscher Ingenieure, 1898,42(29): 797-807.
[20] UKADGAONKER V G, AWASARE P J. A novel method of stress analysis of an infinite plate with circular hole with uniform loading at infinity[J].Indian Journal of Science and Technology, 1993,31: 539-541.
[21] WANG W S, YUAN H T, LI X, et al. Stress concentration and damage factor due to central elliptical hole in functionally graded panels subjected to uniform tensile traction[J].Materials, 2019,12(3): 422.
[22] UKADGAONKER V G, AWASARE P J. A novel method of stress analysis of an infinite plate with rounded corners of a rectangular hole under uniform edge loading[J].Indian Journal of Engineering and Materials Sciences, 1994,1: 17-25.
[23] REZAEEPAZH J, JAFARI M. Stress concentration in metallic plates with special shaped cutout[J].International Journal of Mechanical Sciences, 2010,52(1): 96-102.
[24] DAI L C, GUO W L, WANG X. Stress concentration at an elliptic hole in transversely isotropic piezoelectric solids[J].International Journal of Solids and Structures, 2006,43(6): 1818-1831.
[25] 崔建斌, 姬安召, 熊贵明. 基于Schwarz-Christoffel变换的圆形隧道围岩应力分布特征研究[J]. 应用数学和力学, 2019,40(10): 1089-1098.(CUI Jianbin, JI Anzhao, XIONG Guiming. Research on surrounding rock stress distributions for circular tunnels based on the Schwarz-Christoffel transformation[J].Applied Mathematics and Mechanics, 2019,40(10): 1089-1098.(in Chinese))
[26] YANG J, LI X, DING S H. Anti-plane analysis of a circular hole with three unequal cracks in one-dimensional hexagonal piezoelectric quasicrystals[J].Chinese Journal of Engineering Mathematics, 2016,33(2): 184-198.
[27] 杨娟, 李星, 周跃亭. 一维六方压电准晶中圆孔边周期裂纹分析[J]. 振动与冲击, 2019,38(18): 62-71.(YANG Juan, LI Xing, ZHOU Yueting. Analysis of periodic cracks emanating from a circular hole in one-dimensional hexagonal piezoelectric quasicrystals[J].Journal of Vibration and Shock, 2019,38(18): 62-71.(in Chinese))
[28] YU J, GUO J H, XING Y M. Complex variable method for an anti-plane elliptical cavity of one-dimensional hexagonal piezoelectric quasicrystals[J].Chinese Journal of Aeronautics, 2015,28(4): 1287-1295.
[29] 樊世旺, 郭俊宏. 一维六方压电准晶三角形孔边裂纹反平面问题[J]. 应用力学学报, 2016,33(3): 421-426.(FAN Shiwang, GUO Junhong. Anti-plane problem of an edge crack emanating from a triangle hole in one-dimensional hexagonal piezoelectric quasicrystals[J].Chinese Journal of Applied Mechanics, 2016,33(3): 421-426.(in Chinese))
[30] 白巧梅, 丁生虎. 一维六方准晶中正六边形孔边裂纹的反平面问题[J]. 应用数学和力学, 2019,40(10): 1071-1080.(BAI Qiaomei, DING Shenghu. An anti-plane problem of cracks at edges of regular hexagonal holes in 1D hexagonal piezoelectric quasicrystals[J].Applied Mathematics and Mechanics, 2019,40(10): 1071-1080.(in Chinese))
[31] GUO J H, LU Z X. Exact solution of four cracks originating from an elliptical hole in one-dimensional hexagonal quasicrystals[J].Applied Mathematics and Computation, 2011,217(22): 9397-9403.
[32] MUSKHELISHVILI N I.Some Fundamental Problems of the Mathematical Theory of Elasticity[M]. Moscow: Nauka, 1966.
[33] 路见可. 平面弹性复变方法[M]. 武汉: 武汉大学出版社, 2002.(LU Jianke.Plane Elastic Complex Method[M]. Wuhan: Wuhan University Press, 2002.(in Chinese))
[34] SHARMA D S. Stress distribution around polygonal holes[J].International Journal of Mechanical Sciences, 2012,65(1): 115-124.
[35] 邵阳, 郭俊宏. 一维六方准晶中正方形孔边双裂纹的反平面问题[J]. 内蒙古工业大学学报, 2014,33(2): 81-87.(SHAO Yang, GUO Junhong. Anti-plane analysis of double cracks originating from a square hole in one-dimensional hexagonal quasicrystals[J].Journal of Inner Mongolia University of Technology, 2014,33(2): 81-87.(in Chinese))
[36] GUO J H, LIU G T. Stress analysis of the problem about a circular hole with asymmetry collinear cracks[J].Journal of Inner Mongolia Normal University, 2007,36(4): 418-422.