引 言
润湿性是固体表面的重要性质,主要由固体表面的几何结构和化学成分共同决定.近年来,伴随着软物质领域的快速发展,物体表界面效应的研究已经引起了科学家和工程师的密切关注,重要过程之一就是表面润湿现象[1-3],主要表现于液体在固体或液体基质上的润湿.据不完全统计,润湿状态共有64种[4],研究固体表面的润湿性对于理解石油开采、印刷和喷漆、表面防水、昆虫在水面上的移动以及角膜润滑和液体运输等过程具有重要作用[5-9].
Laplace方程和Young方程是毛细力与浸润领域的经典方程,而杨氏定律和Neumann三角广泛用于解释润湿现象.刚性基底上润湿的杨氏定律和液体基底上润湿的Neumann三角是两个主要结果.在刚性基底上,软层表面的接触角由Young 方程γsv=γsl+γlvcos θ给出,这是总自由界面能最小化的结果,这里γsv,γsl,γlv分别是固-气、固-液和液-气界面的表面自由能[5,8,10].在液体基底上,接触角θ由水平方向上的表面能平衡决定,如果基底的弹性模量较大,则液滴采用熟悉的球帽形,如果基底的模量降低,则基底会被接触线的垂直分量拉成尖状,三相界面的排列使接触线上面内外的表面张力平衡[11-14].在某种意义下,它们是连续体湿润问题的两个极端,杨氏定律给出了无限硬基底的极限行为,而Neumann三角给出了流体基底的结果.对于小液滴而言,可忽略重力影响,并且表面张力和界面能是等价的.
Jerison等[15]测量了软硅胶薄膜在大水滴下的变形,他们的结果表明表面变形符合线性相关理论,其中包括由于基板表面张力引起的面外恢复力.Style等[16]将其结果推广到任意半径的液滴引起的基底变形,对于各种尺寸的液滴,接触线附近的微观行为遵循Neumann结构,以实现局部力平衡,但没有探究接触角和梯度对于变形的影响.Cao等[13]利用分子动力学模拟方法研究了凝胶状基底与聚合物液滴接触的宏观和微观特征,仍没有考虑梯度对基底变形的具体影响.理论和实验均表明梯度会诱导液滴的运动[17-18],如接触角梯度、曲率梯度、弹性模量梯度和表面能梯度,这是因为梯度会导致不等的接触角和非对称的固体变形,从而对液滴产生作用力,引起液滴的运动.所以,研究梯度对于薄基变形的影响是有必要的.此外,三相接触线处,线张力对小尺度液滴的润湿性[19]具有重要的作用.
基于以上分析,我们引入了线张力,研究了液滴引起的各向同性、指数型和幂型梯度薄基的变形情况,利用积分变换法求解了变形的本构方程,给出了基底变形的位移表达式,并得出了数值结果,讨论了弹性模量、梯度、线张力和液滴尺寸对于基底变形的影响.本文的研究结果对于微流体器件的设计和研发具有潜在的应用价值.
1 模型建立与基本方程
无柄近半球液滴放置在厚度为h且横向无限大的薄基上,基底下底面固定在刚性表面上,当系统处于平衡时建立模型,如图1所示.
假设模型为柱型轴对称,则在柱坐标系中,基底变形的控制方程为稳态Navier方程:
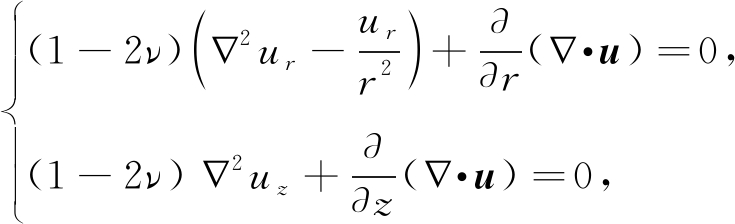
(1)
其中ur,uz分别是位移u沿r,z轴的分量,ν是Poisson比[20].应力与位移的关系式为
(2)
其中,E为弹性模量.
由于软固体底面上的刚性约束,所以对于所有r,位移边界条件为
uz(r,0)=0.
(3)
利用Fourier级数展开将本构方程转化为常微分方程,解得广义弹性常数,遵循Xu等[21]所使用的方法,利用广义弹性常数Qij(s,h,z)将表面应力与基底位移联系起来,如下式:
(4)
其中Pij(s,z),Mij(s,z)见附录A,重复下标表示求和.于是
(5)
其中A11(s,h,z),A12(s,h,z),A21(s,h,z),A22(s,h,z)见附录B.所以表面法向的广义弹性常数为
(6)
其中![]() 见附录B.当ν=0.5时,式(6)退化为
见附录B.当ν=0.5时,式(6)退化为
(7)
与文献[15]的结果一致.
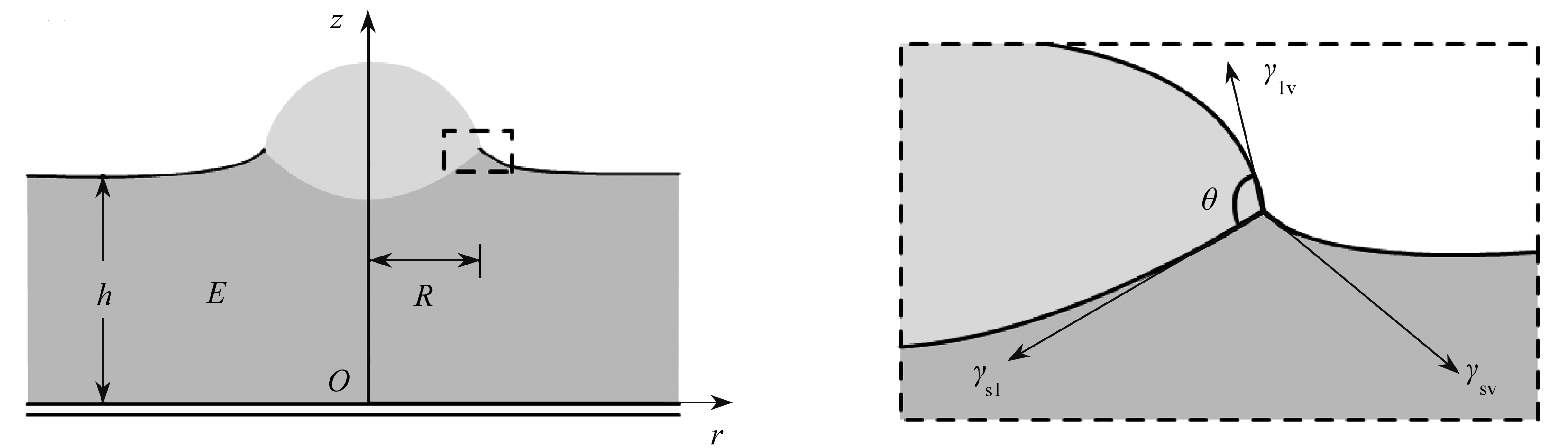
(a) 无柄液滴与软固体接触示意图 (b) 三相接触线附近示意图,这里γsl=γsv
(a) Schematic diagram of the contact between (b) Schematic diagram of 3 contact lines, a sessile droplet and a soft substrateγsl=γsv
图1 模型示意图
Fig. 1 The schematic diagram of the contact model
为准确描述基底的变形, 消除原点处的应力奇异性, 确保法向位移不会发散, 需引进线性表面张力[15-16,22]:
其中γs为固-气表面张力γsv(或固-液表面张力γsl).则表面张力的法向广义弹性常数变为

(8)
对于原点为O的所有r,液滴在软层表面法向上施加的牵引力为
σzz(r,h)=γlvsin(θ)δ(r-R)-PH(R-r),
(9)
其中δ(x)和H(x)分别是Dirac delta函数和Heaviside阶跃函数,γlv为液-气表面张力,R为液滴半径,P=2γlvsin(θ)/R为液滴内部的Laplace压力.
实际上,液滴边界三相接触线上还有一项能量,即线张力λ.在考虑线张力对液滴接触角的贡献时,被修正的Young方程可以表示为[19,23]
(10)
从上述方程中可以看出,当液滴尺寸比较小(微纳米级)时,λ/γlv的影响不可忽略.文献[15-16]均假设γsl=γsv=γs,是因为它们考虑的近半球液滴接触角接近90°,但文献[15]实验测得的接触角为105°,假设和实验存在一定的误差,当我们引进线张力后,一定程度上修正了这个误差.因此我们继续沿用这个假设,则式(10)变为cos θ=-λ/(Rγlv),由三角恒等式可得
(11)
2 模 型 求 解
忽略表面切向牵引力σzr(r,z),则软层的变形仅由法向牵引力σzz(r,z)引起,薄基变形位移为[16]
(12)
式中![]() 这里H0是0阶Hankel变换.将式(9)、(11)代入式(12)得液滴引起的软层变形的法向位移为
这里H0是0阶Hankel变换.将式(9)、(11)代入式(12)得液滴引起的软层变形的法向位移为
(13)
其中
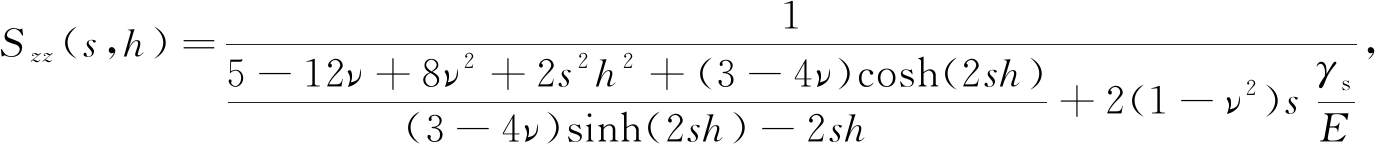
(14)
式中J0和J1分别是第一类0阶和1阶Bessel函数.当液滴为半球形时,即θ=π/2,法向位移退化为文献[16]中的结果,当不考虑线张力的影响时,即λ=0,法向位移仍退化为文献[16]的结果.此外,不考虑线张力,且固-液界面和固-气界面的表面张力不同时,基底变形情况可以通过对偶积分方程得到[24].
引进如下无量纲变量:
(15)
将式(15)代入式(13)和式(14),得无量纲法向位移表达式为
(16)
式中
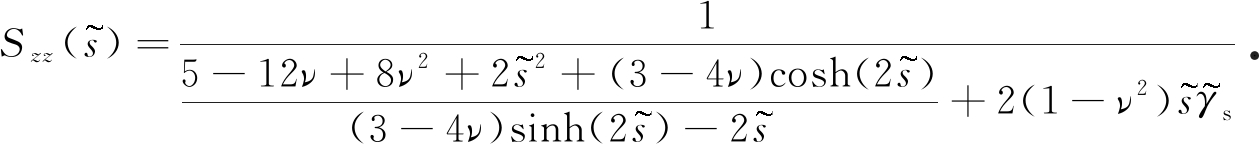
(17)
式(16)是双重Bessel函数积分,对于比较复杂的被积函数,该类积分的解析解一般很难求得,很多学者对其数值解进行了研究[25-26],基于他们的贡献,我们给出了式(16)的数值解.
基底材料参数呈现梯度变化时,会诱导液滴的运动,但是基底的变形情况会是怎样的呢?本文做了具体的研究.当基底弹性模量E随坐标变量z呈现梯度变化,且Poisson比不随z变化时,基底变形的控制方程仍为稳态Navier方程.下面探讨基体弹性模量呈梯度变化时,液滴对变形的影响.
 当弹性模量呈现指数形式变化时:
当弹性模量呈现指数形式变化时:
E(z)=E0eaz,
其中E0为参考弹性模量,a表示与功能梯度材料性质相关的参数,当a为零时,弹性模量退化为E0,即退化为均匀各向同性弹性材料.此时软层变形的无量纲法向位移为
(18)
其中
(19)
这里
(20)
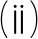 当弹性模量呈现幂函数变化时[27]:
当弹性模量呈现幂函数变化时[27]:
E(z)=E0(z/c0)k, 0≤k≤1,
其中,E0为参考弹性模量,c0(c0>0)为表征模量变化率的特征深度,k为梯度变化指数.材料的弹性模量随深度而递增,在深度为c0处达到E0,并且存在两种特殊情况:当k=0时,软基底退化为均匀各向同性材料;当k=1,ν=0.5时,软基底退化为线性梯度不可压缩性材料,即Gibson材料[28].
引入无量纲参量![]() 此时软层变形的无量纲法向位移为
此时软层变形的无量纲法向位移为
(21)
其中
(22)
![]() 见式(20).注意,以上表达式下标中的e、p分别代表弹性模量为指数型和幂型的情况.
见式(20).注意,以上表达式下标中的e、p分别代表弹性模量为指数型和幂型的情况.
3 数值结果与讨论
设薄基Poisson比ν=0.5,厚度h=5×10-5 m,液-气表面张力γlv=0.04 N·m-1,固-气(固-液)表面张力γs=0.06 N·m-1,由![]() 量纲分析可知,弹性模量明显的影响范围为103 Pa.基于以上数据,当液滴半径R和基底厚度h满足R/h=Ο(10)时,给出以下数值结果.
量纲分析可知,弹性模量明显的影响范围为103 Pa.基于以上数据,当液滴半径R和基底厚度h满足R/h=Ο(10)时,给出以下数值结果.
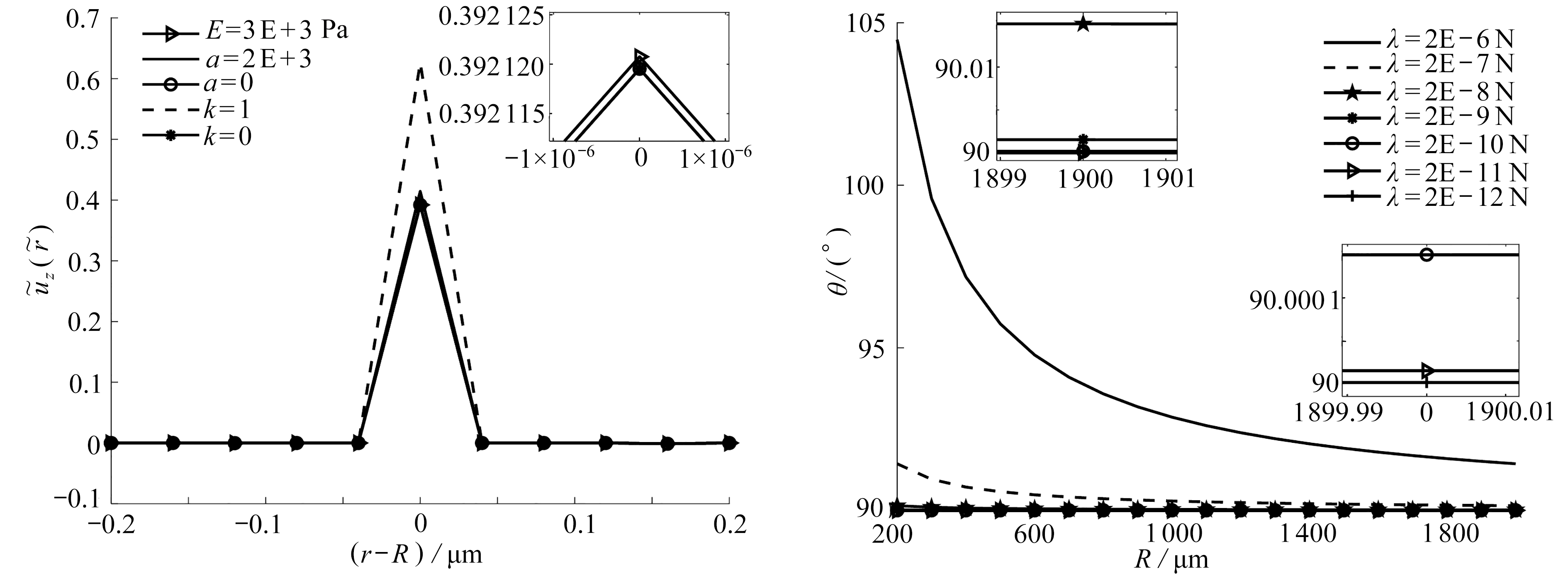
图2 E=3 kPa,R=200 μm,λ=2×10-8 Ν,梯度型 图3 接触角随液滴半径和线张力 基底变形的一般情形和退化结果 能量的变化关系
Fig. 2 E=3 kPa,R=200 μm,λ=2×10-8 Ν, Fig. 3 The relationship between the contact angle, the general case and the degenerate result the droplet radius and the linear of the gradient substrate deformation tension energy
选取文献[16]中参数的值,绘制图2(右箭头线代表文献[16]中的结果,空心圆线和星号线分别代表指数型和幂型梯度的退化结果,其他线为梯度型一般结果),从小图中可以看出,a=0时的指数型梯度与k=0时的幂型梯度的位移退化结果与文献[16]中均匀各向同性基底的结果非常接近,误差量级在10-6范围,故此说明了本文推广结果的正确性.
理论预估和实验测得的线张力大小的量级范围为10-12 N~10-6 Ν[29],因此我们研究了在此范围内接触角随液滴半径和线张力能量的变化.由图3可知,接触角随着线张力的增大而增大,随着半径的增大而减小,无限逼近于90°.当半径较小时,线张力对接触角的影响是比较大的,所以本文引入线张力对于表面变形的研究是有必要的.
此外,图中结果显示了线张力对接触角的影响范围在90°~105°间,和文献[15]假设与试验测得的接触角误差刚好吻合,这也验证了我们假设γsl=γsv=γs成立的合理性.
(a) 不同量级的线张力λ对基底变形的影响 (b) 同一量级的λ变化对位移的影响
(a) The influence of different orders of linear tension (b) The influence of different λ valuesλ on the substrate deformation on the displacement
图4 E=2 kPa,R=200 μm,线张力λ对基底变形的影响
Fig. 4 E=2 kPa,R=200 μm, the influence of linear tension λ on the substrate deformation
(a) E对基底位移的影响 (b) R和λ变化时基底位移的变化
(a) The influence of E on the displacement (b) The changes of the displacement of the substrate of the substrate with R and λ
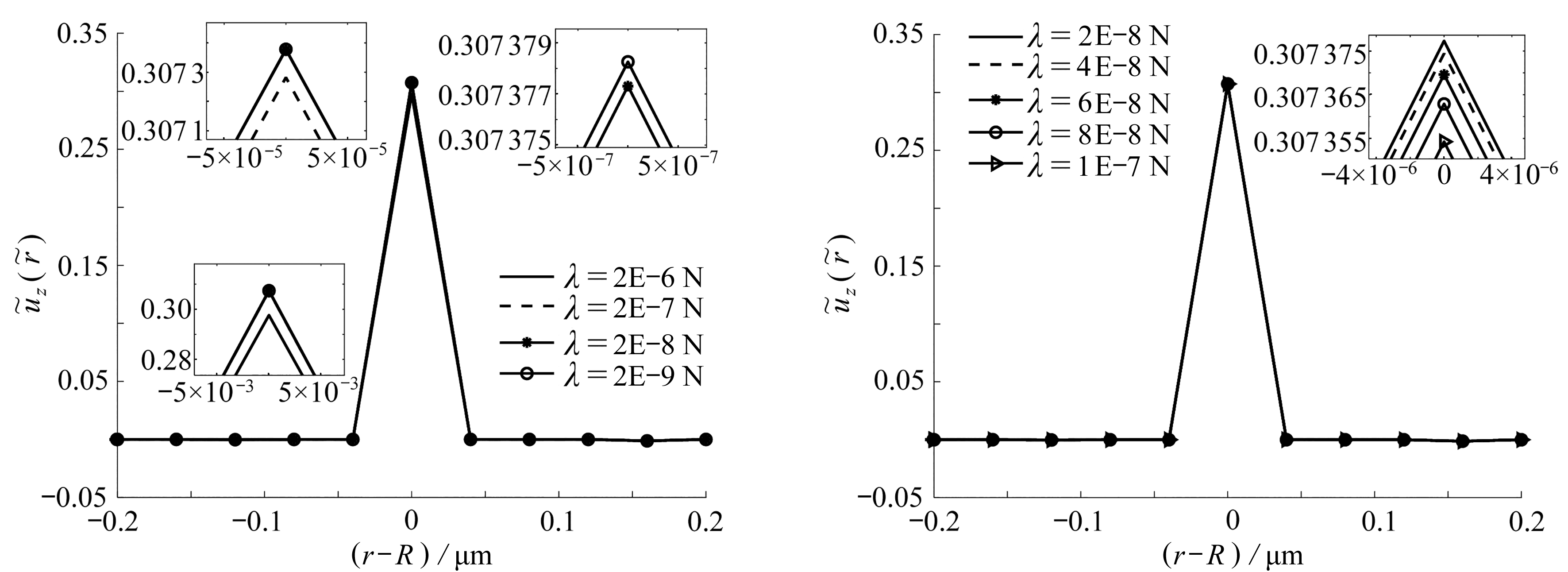
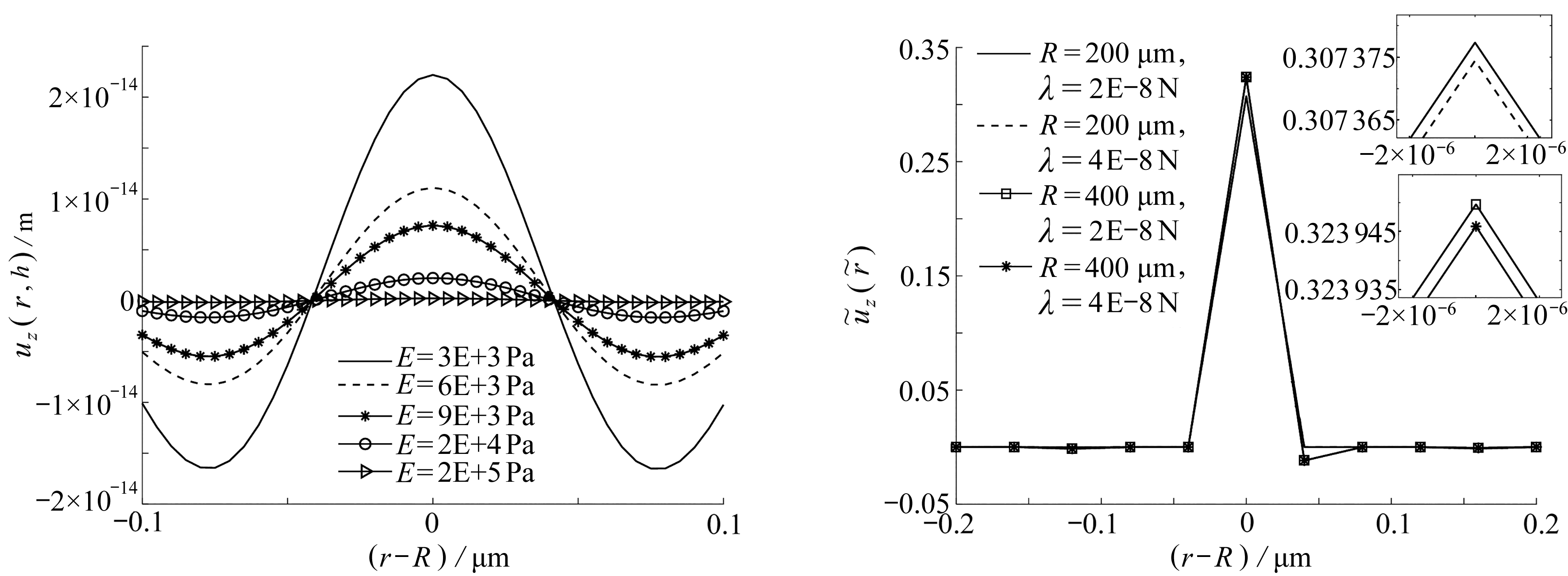
图5 基底弹性模量E、线张力λ、液滴半径R变化对基底变形的影响
Fig. 5 The influences of the changes of elastic modulus E, linear tension λand droplet radius R on the substrate deformation
1) 非梯度变化
由于cos θ=-λ/(Rγlv),所以线张力的量级≤Ο(10-6 Ν),而当λ>O(10-9 Ν)时,λ对变形的贡献非常微弱,可以忽略,因此本文研究了线张力在10-9 N~10-6 Ν不同量级下对基底变形的影响.由图4(a)可知,当λ/(Rγlv)从O(1)变化至O(10-3)时,线张力对位移的影响非常小,从热力学的观点来看,在固体表面的一个小的无座液滴上的正张力会减少三相线的长度,从而增加接触角,这可能导致液滴大部分传热,能量发生耗散.图4(b)绘制了λ在10-8 Ν下对变形的影响,从图中可知,半径在微米级时,图像重叠在一起,当把局部放大后可以得知,线张力越小,对变形的影响越大.
图5显示了对于同样的线张力和液滴半径,基底弹性模量越小,湿润脊的峰值越高,基底的变形也越大,而对于同样的线张力和基底弹性模量,表面的变形会随着液滴半径的增大而增大.不论弹性模量、线张力和液滴半径怎么变化,位移的变化基本上呈对称态,与第1节对模型假设的柱型轴对称一致,并且湿润脊随着液滴半径的减小而变得更加对称,这是由于液滴半径越大,会导致接触角发生微弱的不等现象,从而导致液体偏离对称轴,产生不对称的变形.

(a) R和a变化时位移的变化(b) λ和a变化时位移的变化
(a) The change of displacement with R and a (b) The change of displacement with λ and a
图6 E0=2 kPa,梯度指数参数a、线张力λ、液滴半径R变化对基底变形的影响
Fig. 6 E0=2 kPa, the influences of gradient index parameter a, linear tension λ and droplet radius R on the substrate deformation
(a) R和c0变化时位移的变化(b) λ和c0变化时位移的变化
(a) The change of the displacement with R and c0(b) The change of the displacement with λ and c0
图7 E0=2 kPa,k=0.5,特征深度c0、线张力λ、液滴半径R变化对基底变形的影响
Fig. 7 E0=2 kPa,k=0.5,the influences of characteristic depth c0,linear tension λand droplet radius R on the substrate deformation
2) 指数型梯度变化
从图6可知,液滴半径增大时,表面变形也随之增大,梯度指数参数a增大时,湿润脊的峰值更大,线张力越小,变形越大.液滴半径越小,湿润脊变得更加对称,这与无梯度的结果保持一致,说明基底模量的变化并不会影响到液滴半径对变形的贡献.
3) 幂型梯度变化
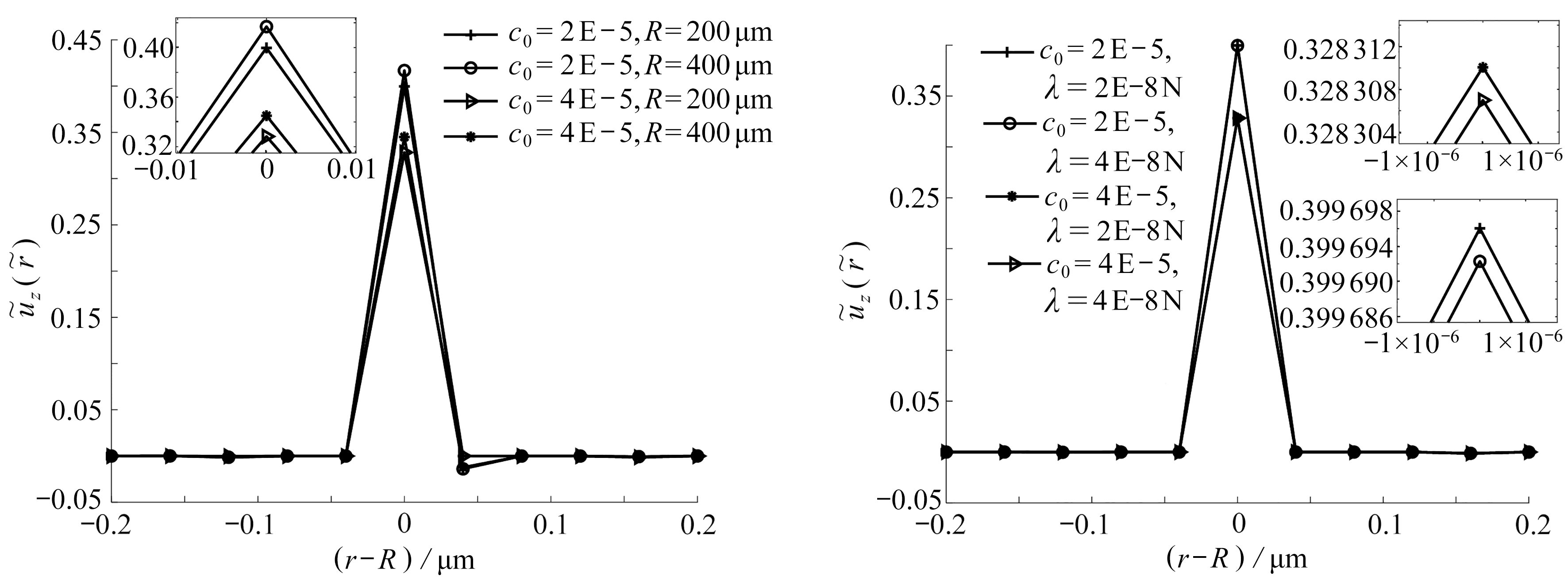
由图7可知,湿润脊的峰脊高度随特征深度的增加而减小,即特征深度越小,变形越大.线张力越小,变形越大,半径对变形的影响与上述一致.
由图8可知,半径对变形的贡献与上述一致,此处不再赘述.对于同样的线张力和液滴半径,梯度指数k越大,位移变化幅度越大,峰脊越高.线张力越小,变形越大.当k=1,ν=0.5时,软基底退化为Gibson材料,此时基底的变形情况也可从图中获得.
此外,图4~8中湿润脊的形状与模型示意图1中基底变形的形状吻合,尤其是在三相界面处的变形,也印证了本文结果的正确性.
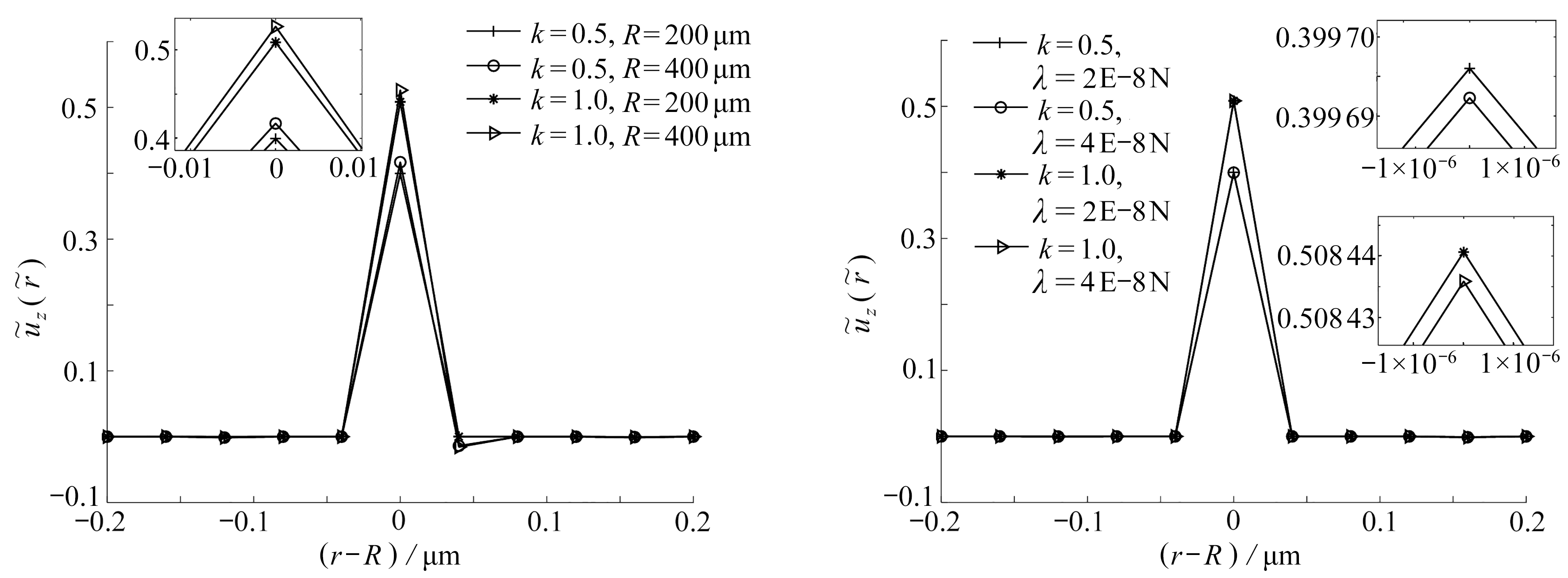
(a) R和k变化时位移的变化(b) λ和k变化时位移的变化
(a) The change of the displacement with R and k(b) The change of the displacement with λ and k
图8 E0=2 kPa,c0=2×10-5,梯度指数k、线张力λ、液滴半径R变化对基底变形的影响
Fig. 8 E0=2 kPa,c0=2×10-5,the influences of gradient index k,linear tension λand droplet radius R on the substrate deformation
4 结 论
本文研究了液滴引起的梯度薄基的法向变形,利用积分变换法求解了变形的本构方程,给出了变形位移的表达式.通过数值求解位移表达式得出,基底弹性模量越大,湿润脊的峰值越低,基底的变形也越小.但弹性模量不会影响峰脊的形状,这与文献[15]中的结果一致.液滴半径越大,湿润脊越高,变形也越大.相反,半径越小,湿润脊会变得更对称.此外,线张力越小,变形越大,并且线张力对表面变形的贡献随着液滴半径量级的减小而逐渐增大.梯度指数越大,湿润脊峰值越大,变形也越大.特征深度越小,变形越大.本文的结果对软器件的设计和制造具有潜在的应用价值.
附 录 A
位移场的控制方程为稳态Navier方程:
(A1)
式中ν为基底材料的Poisson比.上式可通过用Fourier级数表示位移来求解,令
(A2)
其中α,β分别表示x,y方向的波数,![]() 分别是u,v,w的复Fourier系数,i为虚数单位.将式(A2)代入式(A1)并化简得[30]
分别是u,v,w的复Fourier系数,i为虚数单位.将式(A2)代入式(A1)并化简得[30]
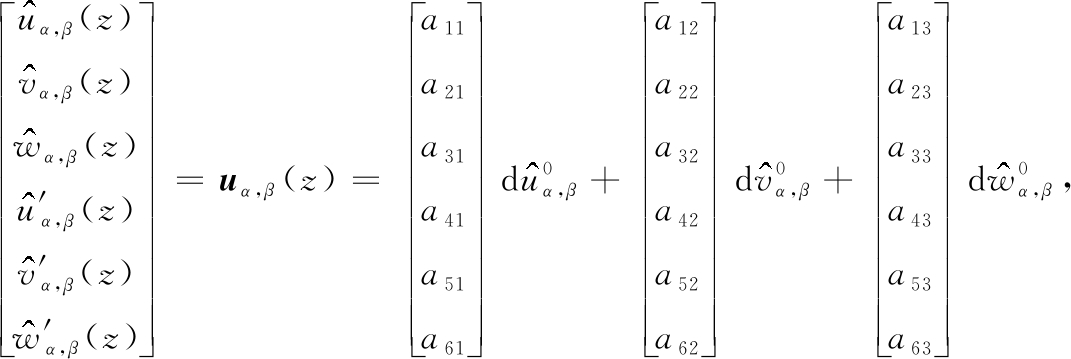
(A3)
其中![]() 分别是u,v,w在z=0处的复Fourier系数的边值,并且
分别是u,v,w在z=0处的复Fourier系数的边值,并且


式中![]() 将应力Fourier展开得
将应力Fourier展开得
广义Hooke定律为
由Fourier变换得
则

其中
M=(aij)3×3, i, j=1,2,3.
所以
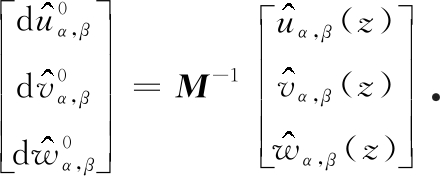
(A4)
由式(A3)知

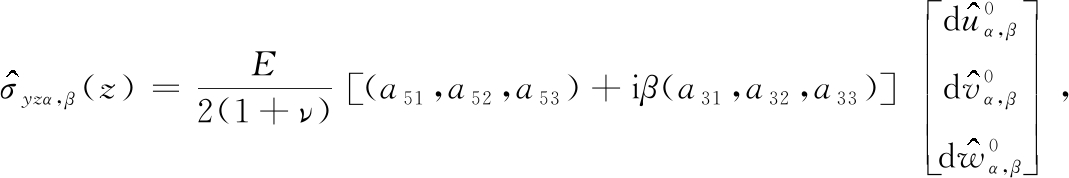
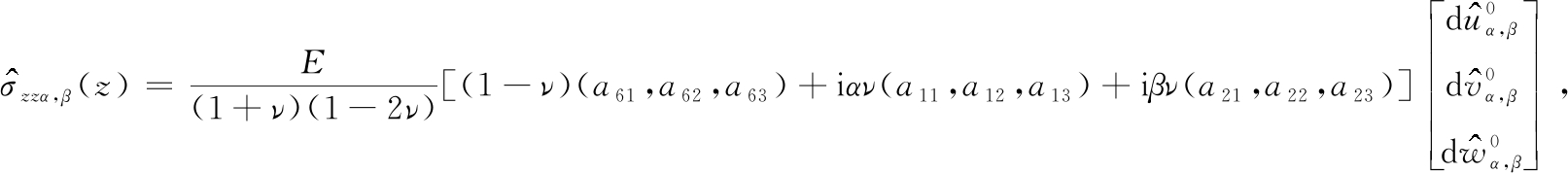
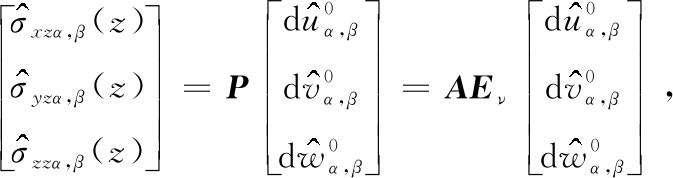
(A5)
其中A=A1+A2,


式中
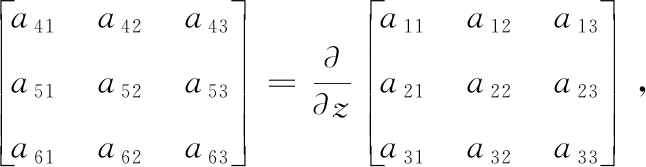
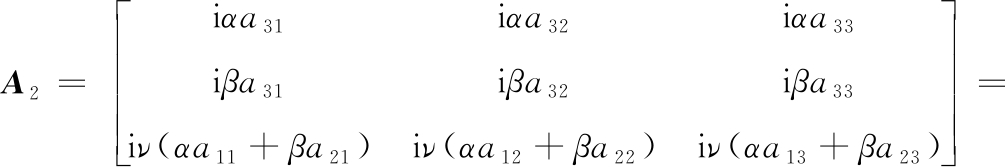

由式(A4)和式(A5)得
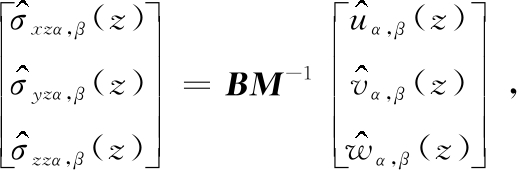
其中
B=EνA=Eν(A1+A2)=
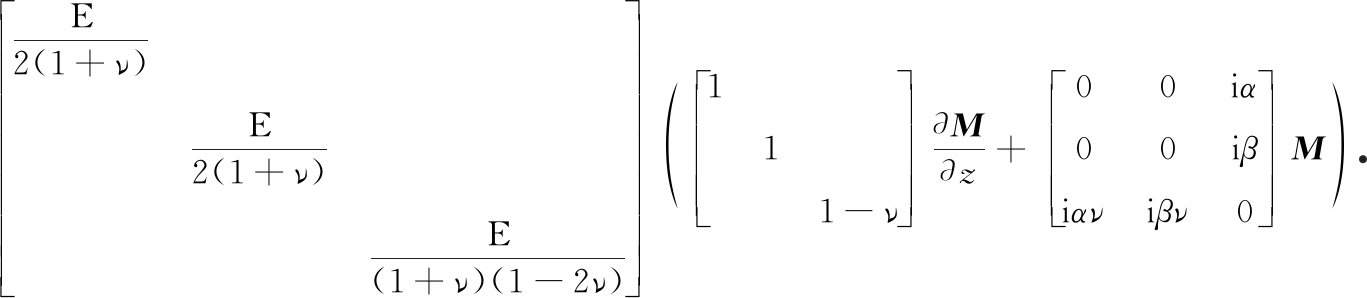
令Qij=BM-1,有
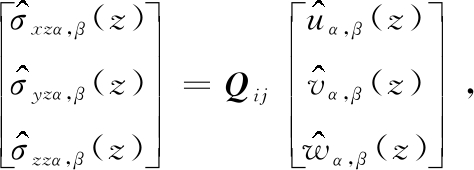
由Fourier逆变换得
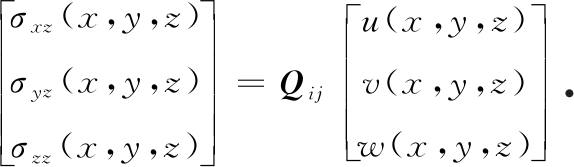
(A6)
对于二维向量u=(ur,uz),其中ur,uz分别为径向位移和法向位移, 且x方向的波数α为零,令β=s有
其中

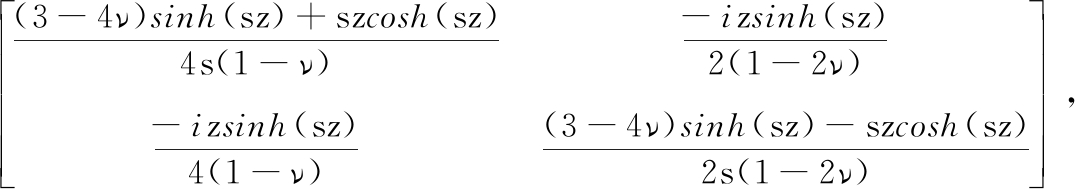
(A7)
则二维情形的广义弹性常数为
(A8)
附 录 B
A11(s,h,z)=(6-14ν+8ν2)cosh(sh)sinh(sz)+(-3sh+sz+4shν)sinh(sh)sinh(sz)+
2szcosh(sh)cosh(sz)-2sνzcosh(sh+sz)+hs2zsinh(sz-sh),
A12(s,h,z)=-i[(3-10ν+8ν2)sinh(sh)sinh(sz)+(-3sh+2sz+4shν)cosh(sh)sinh(sz)+
szsinh(sh)cosh(sz)-2sνzsinh(sz+sh)-hs2zcosh(sz-sh)],
A21(s,h,z)=i[(3-10ν+8ν2)sinh(sh)sinh(sz)+(3sh-2sz-4shν)cosh(sh)sinh(sz)-
szsinh(sh)cosh(sz)+2sνzsinh(sz+sh)-hs2zcosh(sz-sh)],
A22(s,h,z)=(6-14ν+8ν2)cosh(sh)sinh(sz)+(3sh-sz-4shν)sinh(sh)sinh(sz)-
2szcosh(sh)cosh(sz)+2sνzcosh(sh+sz)+hs2zsinh(sz-sh),
[1] BUTTH J, GRAF K, KAPPL M. Physics and Chemistry of Interfaces[M]. Wiley-VCH, 2003.
[2] KUMAR G, PRABHU K N. Review of non-reactive and reactive wetting of liquids on surfaces[J]. Advances in Colloid and Interface Science, 2007, 133: 61-89.
[3] QUERE D. Wetting and roughness[J]. Annual Review of Materials Research, 2008, 38: 71-99.
[4] LIU M J, WANG S T, JIANG L. Nature-inspired superwettability systems[J]. Nature Reviews Materials, 2017, 2(7): 17036.
[5] DE GENNES P G, BROCHARD-WYART F, QUERE D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves[M]. Berlin: Springer, 2010.
[6] SHULL K R. Contact mechanics and the adhesion of soft solids[J]. Materials Science and Engineering R: Reports, 2002, 36(1): 1-45.
[7] ROMAN B, BICO J. Elasto-capillarity: deforming an elastic structure with a liquid droplet[J]. Journal of Physics Condensed Matter, 2010, 22(49): 493101.
[8] ISRAELACHVILI J N. Intermolecular and Surface Forces[M]. London: Academic Press, 1992.
[9] WANG H X, ZHOU H, NIU H T. Dual-layer superamphi-phobic/superhydrophobic-oleophilic nanofibrous membranes with unidirectional oil-transport ability and strengthened oil-water separation performance[J]. Advanced Materials Interfaces, 2015, 2(4): 1400506.
[10] YOUNG T. An essay on the cohesion of fluids[J]. Philosophical Transactions of the Royal Society of London, 1805, 95: 65-87.
[11] LESTER G. Contact angles of liquids at deformable solid surfaces[J]. Journal of Colloid Science, 1961, 16(4): 315-326.
[12] TWOHIG T, MAY S, CROLL A B. Microscopic details of a fluid/thin film triple line[J]. Soft Matter, 2018, 14: 7492-7499.
[13] CAO Z, DOBRYNIN A V. Polymeric droplets on soft surfaces: from Neumann’s triangle to Young’s law[J]. Macromolecules, 2015, 48(2):443-451.
[14] VAN GORCUM M, KARPITSCHKA S, ANDREOTTI B, et al. Spreading on viscoelastic solids: are contact angles selected by Neumann’s law?[J]. Soft Matter, 2020, 16(5): 1306-1322.
[15] JERISON E R, XU Y, WILEN L A, et al. Deformation of an elastic substrate by a three-phase contact line[J]. Physical Review Letters, 2011, 106: 186103.
[16] STYLE R W, DUFRESNE E R. Static wetting on deformable substrates, from liquids to soft solids[J]. Soft Matter, 2012, 8(27): 7177-7184.
[17] 王宏. 梯度表面能材料上液滴运动及滴状凝结换热[D]. 博士学位论文. 重庆: 重庆大学, 2008.(WANG Hong. Motion of droplets and dropwise condensation on the gradient surface[D]. PhD Thesis. Chongqing: Chongqing University, 2008.(in Chinese))
[18] BARDALLA, CHEN S Y, DANIELS K E, et al. Gradient-induced droplet motion over soft solids[J]. IMA Journal of Applied Mathematics, 2019, 85(3): 09413.
[19] 吕存景, 殷雅俊, 郑泉水. 线张力作用下微纳米尺度液滴的非线性粘附[J]. 应用数学和力学, 2008, 29(10): 1135-1146.(LÜ Cunjing, YIN Yajun, ZHENG Quanshui. Nonlinear effects of line tension in adhesion of small droplets[J]. Applied Mathematics and Mechanics, 2008, 29(10): 1135-1146.(in Chinese))
[20] IRGENS F. Continuum Mechanics[M]. Berlin: Springer-Verlag, 2008.
[21] XU Y, ENGL W C, JERISON E R, et al. Imaging in-plane and normal stresses near an interface crack using traction force microscopy[J]. Proc Natl Acad Sci USA, 2010, 107(34): 14964-14967.
[22] LONG D, AJDARI A, LEIBLER L. Static and dynamic wetting properties of thin rubber films[J]. Langmuir, 1996, 12(21): 5221-5230.
[23] 赵亚溥. 表面与界面物理力学[M]. 北京: 科学出版社, 2012: 177.(ZHAO Yapu. Physical Mechanics of Surface and Interface[M]. Beijing: Science Press, 2012: 177.(in Chinese))
[24] BOSTWICK J B, SHEARER M, DANIELS K E. Elastocapillary deformations on partially-wetting substrates: rival contact-line models[J]. Soft Matter, 2014, 10: 7361-7369.
[25] 华军, 蒋延生, 汪文秉. 双重贝塞尔函数积分的数值计算[J]. 煤田地质与勘探, 2001, 29(3): 58-62.(HUA Jun, JIANG Yansheng, WANG Wenbing. The numerical integration of dual Hankel transformation[J]. Coal Geology & Exploration, 2001, 29(3): 58-62.(in Chinese))
[26] LI M, HE W, LI Q, et al. The numerical integration algorithm of dual Bessel function and its application[J]. International Journal of Applied Electromagnetics and Mechanics, 2010, 33: 727-734.
[27] GINNAKOPOULOS A E, SURESH S. Indentation of solids with gradients in elastic properties, part Ⅱ: axisymmetric indentors[J]. International Journal of Solids and Structures, 1997, 34(19): 2393-2428.
[28] GIBSON R E. Some results concerning displacements and stresses in a non-homogeneous elastic half-space[J]. Geotechnique, 1967, 17: 58-67.
[29] AMIRFAZLI A, NEUMANN A W. Status of the three-phase line tension: a reviwe[J]. Advances in Colloid & Interface Science, 2004, 110(3): 121-141.
[30] DEL ![]() J C, MEILI R, ALONSO-LATORRE B, et al. Spatio-temporal analysis of eukaryotic cell motility by improved force cytometry[J]. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104: 13343-13348.
J C, MEILI R, ALONSO-LATORRE B, et al. Spatio-temporal analysis of eukaryotic cell motility by improved force cytometry[J]. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104: 13343-13348.