引 言
在本文中,我们研究以下初边值问题:
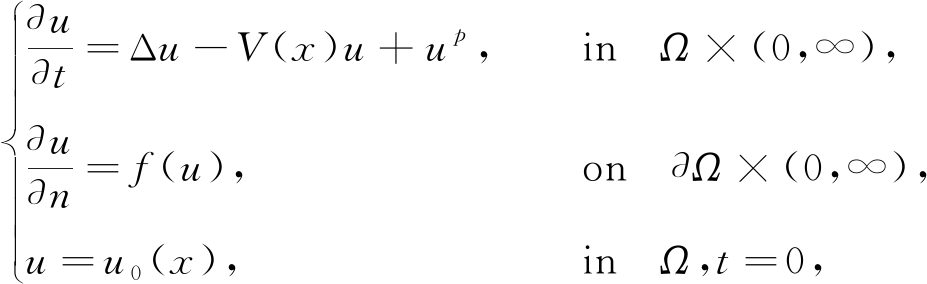
(1)
其中Ω⊂RN(N≥2)是一个有界凸区域且具有光滑的边界∂Ω,p>0,∂/∂n是∂Ω上的外单位法向导数, f(u)是非负连续函数,u0∈C(Ω),V(x)~w|x|-σ,w,σ>0.
许多实际模型都是受偏微方程控制的,人们从数学的角度来研究这些模型时首先关心的是这些模型的适定性.因此在过去的几十年,抛物方程解的存在性及爆破现象受到了广泛关注,本文展示几个与我们研究的问题相关的一些结果.Gómez等[1]研究了具有非线性条件的热量方程:
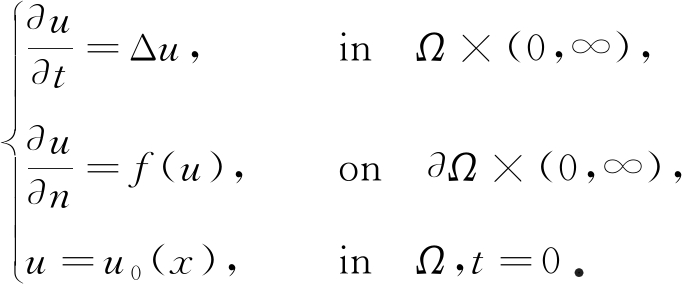
他们研究了非负解的长时间行为,如果Ω=BR,证明了解一定会在有限时刻爆破.当Ω是二维的单连通区域时,证明了解仅会在Ω的边界上爆破.当Ω=RN(N≥1)且f(u)=up,p>1+1/N时,Kawakami[2]研究了上述方程的全局解的存在性.在对f(u)给出一些约束条件之后,Payne等[3]证明了爆破时间的下界以及确保爆破不会发生的条件.
Liu等[4]考虑了具有非线性梯度项的抛物方程
![]()
 u|2qdx
u|2qdx
在边界条件
下的爆破现象.应用微分不等式技术,他们获得了爆破时间的下界.更加一般化抛物方程的相关研究见文献[5-8].
考虑到高速飞行的物体对航天飞机表面绝缘层造成的局部损伤,Yang和Zhou[9]提出了具有局部非线性Neumann边界条件的热量方程:
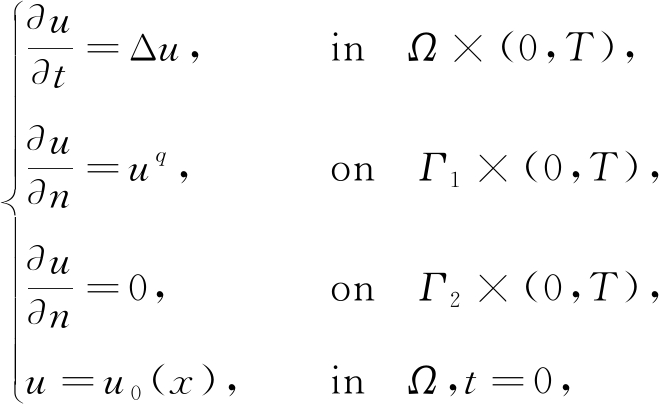
其中![]() 和Γ2是∂Ω的两个互不相交的子集.他们不再需要区域是凸的,证明了解在有限时刻爆破并得到了爆破时间的上下界.
和Γ2是∂Ω的两个互不相交的子集.他们不再需要区域是凸的,证明了解在有限时刻爆破并得到了爆破时间的上下界.
Ishige[10]考虑了Cauchy问题:
其中p>1.他推导了一个被称为Fujita指数的常数p*,并且当p=p*时,证明了该Cauchy问题不存在全局正解.这种类型的研究已经持续了很长一段时间,仍是当前研究的热点,出现了大量最新成果(参见文献[11-15]).受上述文献的启发,本文的主要目的就是在上述工作的基础上研究问题(1)在有界区域上解的存在性,把文献中取得的成果推广到更一般化的热量方程上.本研究的关键之处就是通过对参数p、非线性项f(u)和初始数据进行适当巧妙的假设,以得到解的存在性与非存在性,在爆破的情况下估计爆破时间的上下界.
1 主 要 结 果
这一节,我们将介绍本文取得的主要结果以及证明这些结果所需要的引理.由于非线性项或数据的存在,生物系统中的化学反应、气体点火、多孔介质、Ohm加热和趋化性等问题都表现出爆炸性的增长.对这些问题的研究通常涉及到整体解的存在性/非存在性或解在有限时间内的爆破.所谓的爆破就是指解在有限时间内以某种方式变得无界.例如趋化性模型爆破现象的研究见文献[16-17].此外,Straughan[18]研究了力学问题中的爆炸行为.历史上,对反应扩散方程中爆炸现象的研究始于Kaplan开创性的论文[19].本文就问题(1)进行研究,通过对非线性项以及初始数据作出一定的约束,得到了爆破时间的上界,即:
定理1 设u(x,t)是问题(1)在Ω∈RN(N≥2)上的非负经典解.记F(s)=![]() f(η)dη,并假设
f(η)dη,并假设
uf(u)≤(1+p)F(u).
问题(1)的初始数据满足
ψ(0)![]()
![]()

![]()
若p>1,则不管N=2还是N>2,u(x,t)一定在某个有限时刻t处爆破,并且爆破时间的上界为
其中
需要说明的是定理1的结果对于抛物不等式
仍然是成立的.如果在问题(1)中假设0<p<1,那么定理1就不再成立了.在这种情况下,证明问题(1)的解在任何时刻都是有界的,即解是全局存在的.我们把这个结果写为以下定理.
定理2 设
0<f(u)≤k1uq, 0<q<1.
若0<p<1且V(x)≥w|x|-σ,则问题(1)在Ω∈RN(N≥2)上一定具有全局解.
类似地,定理2的结果对于抛物不等式
仍然有效.
文献中, 在研究解的爆破现象方面积累了大量的方法,包括Fourier系数法、上解技术、Green函数法、测试函数法、加权能量法、对照原理、凹性法.这些方法过去往往用来推导爆破时间的上界.实际上,爆破时间的下界更为重要,因为建模过程具有爆炸性.这种类型的下界逐渐受到重视,出现了一些较新的成果(见文献[5-7,16]).这类研究通常的做法是首先假设问题的解在某个时刻爆破,然后来推导爆破时间的下界.不管这种下界最终是否发生,这种类型的下界都是有意义的.由定理1和定理2可知, 当p=1时问题(1)可能会爆破,此时我们推导爆破时间的下界,并得到了以下定理.
定理3 设
0<f(u)≤k1uq, q>1,
且p=1.如果问题(1)的非负经典解在某个有限时刻t*爆破,则爆破时间的下界由下式给出:
其中N>2时,2q<n<2q/(N(q-1));N=2时,2q<n<q/(2(q-1)).
为了证明上述定理,我们常常会用到以下几个微分不等式.
引理1[20] 令Ω是RN(N≥2)上的一个有界星型区域,![]() 则
则
![]()
 w|dx, k>0.
w|dx, k>0.
引理2[21-22] 令Ω是RN(N≥3)上的一个有界星型区域,有
![]()

![]()
其中Λ1是一个依赖于Ω和N的大于零的常数.
显然,当N=2时引理2就不再成立了,但是我们注意到,李远飞[23]已经证明了
![]()

![]()
其中δ是一个大于零的任意常数,Ω是一个矩形区域.为了证明问题(1)解的存在性,我们再结合文献[24]附录B中的方法,证明当Ω是一个有界的凸区域时上式仍然是成立的,即:
引理3 存在一个依赖于区域Ω⊂R2以及∂Ω的大于零的常数Λ2,使得
![]()

![]()
证明 设P是Ω内的一个点.令P1和P2分别表示过点P平行于x1轴的直线与∂Ω的交点,令Q1和Q2分别表示过点P平行于x2轴的直线与∂Ω的交点.首先,我们注意到
(2)
所以
(3)
类似地,有
(4)
结合式(3)和式(4),有
![]()

![]()
(5)
再利用引理1(N=2)和Hölder不等式,可得
![]()
 v|2dA.
v|2dA.
(6)
在式(6)中取![]() 即可完成引理3的证明.
即可完成引理3的证明.
在接下来的几节,我们将分别给出定理1、定理2和定理3的证明,在最后一节我们将对本文进行总结和后续研究进行展望.
2 定理1的证明
首先我们建立两个辅助函数:
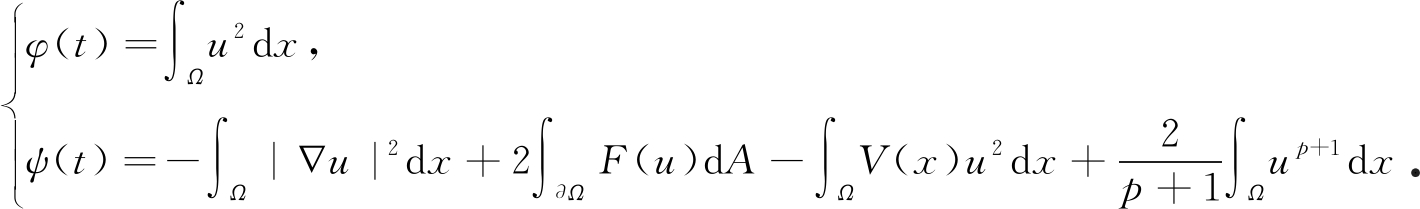
(7)
对φ(t)求导,并利用方程(1)可得
![]()

![]()
(8)
由于p>1以及uf(u)≥(1+p)F(u),所以
![]()

![]()
(9)
再对ψ(t)进行类似的计算,可得
![]()
 u
u
![]()
(10)
又由于
![]()

![]()
即ψ(0)>0,所以由式(10)可知ψ(t)>0.于是由式(8)可得φ′(t)>0.由于![]() 所以φ(t)>0.另一方面,利用Hölder不等式,可得
所以φ(t)>0.另一方面,利用Hölder不等式,可得
(11)
联合式(9)~(11),可得
(1+p)φ′(t)ψ(t)≤2φ(t)ψ′(t),
即
[φ-(1+p)/2(t)ψ(t)]′≥0.
(12)
对式(12)从0到t积分,可得
ψ(t)≥[φ(t)](1+p)/2[φ(0)]-(1+p)/2ψ(0).
(13)
再注意到式(9),由式(13)可得
φ(t)≥(1+p)[φ(t)](1+p)/2[φ(0)]-(1+p)/2ψ(0).
(14)
对式(14)从0到t积分,可得
(15)
由于p>1,由式(15)可知,方程(1)的解必定在某有限时刻发生爆破,且爆破时间的上界可由下式给出:
3 定理2的证明
在本节我们仍然使用上一节中式(7)所定义的φ(t).
1) N>2的情形
利用Hölder不等式和引理2来计算式(8)右边的第四项,有
![]()

![]()
(16)
再利用不等式
并记
由式(16)可得
![]()

![]()
![]()

![]()
(17)
其中ε1是一个大于零的任意常数,r是区域Ω的直径.接下来,我们来处理式(8)右边的第二项,注意到f(u)≤k1uq,0<q<1,利用引理1和Hölder不等式,所以
![]()
 u|dx≤
u|dx≤
![]()

![]()
(18)
与式(17)进行类似的计算,可得
![]()

![]()
(19)
其中ε2是一个大于零的任意常数.取适当的ε1和ε2使得
然后再把式(17)和式(19)代入到式(8)中,可得
(20)
其中
对式(20)进行整理,可得
(21)
注意到0<p,q<1,由式(21)可知问题(1)的解在任何有限时刻不会发生爆破,即存在全局解.否则,如果问题(1)的解在某个时刻t*<∞处爆破,则由式(21)可知,必存在一个时间区间(t0,t*],使得对任意的t∈(t0,t*]有φ′(t)≤0.于是φ(t*)≤φ(t0).这就产生了一个矛盾.
2) N=2的情形
在此种情形下,我们利用引理3来重新计算式(9)右边的第四项,有
![]()

![]()
(22)
与N>2的情形类似,我们可以证明当N=2时问题(1)存在全局解.于是定理2证毕.
4 定理3的证明
在式(8)中取p=1,再注意到f(u)≤k1uq,有
![]()

![]()
(23)
利用引理1和Hölder不等式,可得
![]()
 u|dx≤
u|dx≤
![]()

![]()
![]()
 u|2dx.
u|2dx.
(24)
1) N>2的情形
利用引理2和Hölder不等式,可得
![]()

![]()
![]()

![]()
(25)
其中ε3是一个大于零的任意常数,以及n和N满足条件
在式(25)中利用Young不等式,可得
![]()

![]()
(26)
其中
取适当的ε3使得
然后再把式(26)代入到式(24),最后再把式(24)代入到式(23),可得
(27)
其中
再注意到φ(t)的定义,由式(27)可得
(28)
如果问题(1)在某个有限时刻t*爆破,则通过对式(28)从0到t*积分就可以得到爆破时间的下界,即
(29)
由于q>1,所以(n-2)q>n-2q.因此式(29)右边的积分是收敛的.
2) N=2的情形
此时,我们首先在式(24)中取N=2,有
![]()
 u|2dx.
u|2dx.
(30)
再利用引理3重新计算式(25),有
![]()

![]()
![]()

![]()
(31)
其中2q<n<q/(2(q-1)).用式(31)代替本节N>2情形中的式(25),再经过类似的计算可得爆破时间的下界,即
(32)
这里的C′5,C′6是与C5,C6类似的大于零的常数,但是他们的数值可能与C5,C6稍有差异.
5 总 结
本文首先充分利用微分不等式技术,研究了具有变系数的半线性热量方程解的存在性及爆破现象.这种方法的关键就是建立适当的辅助函数以及巧妙的设置参数,最终使得本文定理较为简单明了地得到了证明.其次,受文献[9]的启发,我们也可以在问题(1)中施加局部非线性边界条件,这样处理会更加符合模型的实际状态,同时使得研究更加有意义.第三,我们注意到Liu[25]研究了Cauchy问题
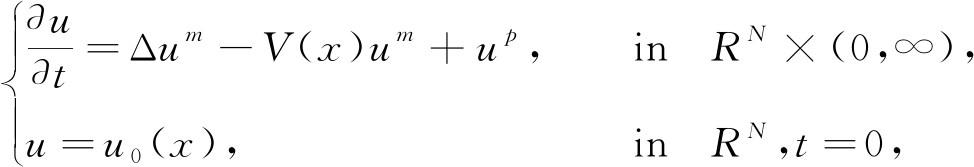
(33)
以及Xiao和Fang[11]研究了具有奇异势项与非局部源拟线性抛物不等式
(34)
和
(35)
这些问题更加复杂,我们假设式(33)~(35)在一个有界区域Ω上满足非线性边界条件,借鉴本文的方法以及巧妙的设置辅助函数,可以进一步研究它们解的存在性,这是接下来可以深入研究的一个方向.
[1] G MEZ J L, MARQUEZ V, WOLANSKI N. Blow up results and localization of blow up points for the heat equation with a nonlinear boundary condition[J]. Journal of Differential Equations, 1991, 92(2): 384-401.
MEZ J L, MARQUEZ V, WOLANSKI N. Blow up results and localization of blow up points for the heat equation with a nonlinear boundary condition[J]. Journal of Differential Equations, 1991, 92(2): 384-401.
[2] KAWAKAMI T. Global existence of solutions for the heat equation with a nonlinear boundary condition[J]. Journal of Mathematical Analysis and Applications, 2010, 368: 320-329.
[3] PAYNE L E, SCHAEFER P W. Bounds for blow-up time for the heat equation under nonlinear boundary conditions[J]. Proceedings of the Royal Society of Edinburgh, 2009, 139(6): 1289-1296.
[4] LIU Y, LUO S G, YE Y H. Blow-up phenomena for a parabolic problem with a gradient nonlinearity under nonlinear boundary condition[J]. Computers & Mathematics With Applications, 2013, 65(8): 1194-1199.
[5] 李远飞. 非线性边界条件下高维抛物方程解的全局存在性及爆破现象[J]. 应用数学学报, 2019, 42(6): 721-735.(LI Yuanfei. Blow-up phenomena and global existences for higher-dimensional parabolic equations under nonlinear boundary conditions[J]. Acta Mathematicae Applicatae Sinica, 2019, 42(6): 721-735.(in Chinese))
[6] LIU Y. Lower bounds for the blow-up time in a nonlocal reaction diffusion problem under nonlinear boundary conditions[J]. Mathematical and Computer Modelling, 2013, 57: 926-931.
[7] LIU D M, MU C L, XIN Q. Lower bounds estimate for the blow-up time of a nonlinear nonlocal porous medium equation[J]. Acta Mathematica Scientia, 2012, 32(3): 1206-1212.
[8] 李远飞. Robin边界条件下更一般化的非线性抛物问题全局解的存在性和爆破[J]. 应用数学学报, 2018, 41(2): 257-267.(LI Yuanfei. Blow-up and global existence of the solution to some more general nonlinear parabolic problems with Robin boundary conditions[J]. Acta Mathematicae Applicatae Sinica, 2018, 41(2): 257-267.(in Chinese))
[9] YANG X, ZHOU Z F. Blow-up problems for the heat equation with a local nonlinear Neumann boundary condition[J]. Journal of Differential Equations, 2016, 261: 2738-2783.
[10] ISHIGE K. On the Fujita exponent for a semilinear heat equation with a potential term[J]. Journal of Mathematical Analysis and Applications, 2008, 344(1): 231-237.
[11] XIAO S P, FANG Z B. Nonexistence of solutions for the quasilinear parabolic differential inequalities with singular potential term and nonlocal source[J]. Journal of Inequalities and Applications, 2020, 2020: 64.
[12] CHUNG S Y, CHOI M J, PARK J H. On the critical set for Fujita type blow-up of solutions to the discrete Laplacian parabolic equations with nonlinear source on networks[J]. Computers and Mathematics With Applications, 2019, 78(6): 1838-1850.
[13] LIU Y, YU T, LI W K. Global well-posedness, asymptotic behavior and blow-up of solutions for a class of degenerate parabolic equations[J]. Nonlinear Analysis, 2020, 196: 111759.
[14] GRILLO G, MURATORI M, PUNZO F. Blow-up and global existence for the porous medium equation with reaction on a class of Cartan-Hadamard manifolds[J]. Journal of Differential Equations, 2019, 266(7): 4305-4336.
[15] HAN Y Z. Blow-up at infinity of solutions to a semilinear heat equation with logarithmic nonlinearity[J]. Journal of Mathematical Analysis and Applications, 2019, 474(1): 513-517.
[16] 李远飞, 雷彩明. 具有非线性边界条件的趋化性模型解的爆破时间下界估计[J]. 应用数学学报, 2015, 38(6): 1097-1102.(LI Yuanfei, LEI Caiming. Lower bound of the blow-up time for a model of chemotaxis with nonlinear boundary condition[J]. Acta Mathematicae Applicatae Sinica, 2015, 38(6): 1097-1102.(in Chinese))
[17] JIANG J, WU H, ZHENG S M. Blow-up for a three dimensional Keller-Segel model with consumption of chemoattractant[J]. Journal of Differential Equations, 2018, 264(8): 5432-5464.
[18] STRAUGHAN B. Explosive Instabilities in Mechanics[M]. Berlin: Springer, 1998.
[19] KAPLAN S. On the growth of solution of quasilinear parabolic equations[J]. Communications on Pure and Applied Mathematics, 1963, 16(3): 305-333.
[20] PAYNE L E, PHILIPPIN G A, VERNIER-PIRO S. Blow-up phenomena for a semilinear heat equation with nonlinear boundary condition, Ⅱ[J]. Nonlinear Analysis: Theory, Methods & Applications, 2010, 73(4): 971-978.
[21] BREZIS H. Analyse Fonctionnelle: Théorie et Applications[M]. London: Pitman Press, 1983.
[22] BREZIS H. Functional Analysis, Sobolev Spaces and Partial Differential Equations[M]. New York: Springer: 2011.
[23] 李远飞. 海洋动力学中二维黏性原始方程组解对热源的收敛性[J]. 应用数学和力学, 2020, 41(3): 339-352.(LI Yuanfei. Convergence results on heat source for 2D viscous primitive equations of ocean dynamics[J]. Applied Mathematics and Mechanics, 2020, 41(3): 339-352.(in Chinese))
[24] LIN C H, PAYNE L E. Continuous dependence on the Soret coefficient for double diffusive convection in Darcy flow[J]. Journal of Mathematical Analysis and Applications, 2008, 342(1): 311-325.
[25] LIU C C. The critical Fujita exponent for a diffusion equation with a potential term[J]. Lithuanian Mathematical Journal, 2014, 54(2): 182-191.