引 言
近几十年来,多智能体的一致性问题受到了前所未有的关注.这与多智能体的分布式一致性在多个领域的广泛应用存在着直接关系[1-6].在诸如传感器网络 、多车辆系统、水下潜航器、无人飞行器的协同控制等领域的应用,也推动了多智能体一致性问题研究的飞速发展[7-8].
对于规模比较大的复杂网络,通过控制所有的节点使其达到一致或同步是相当困难的,而且也非常耗费资源.为了节约控制成本,人们提出了牵制控制策略,即通过控制网络中部分节点从而使网络达到一致或者同步.文献[9-16]研究了牵制复杂网络到相同结构的目标节点问题,并给出了有效的牵制控制策略.文献[15]研究了一类具有非线性耦合的复杂切换系统的牵制控制问题,并通过设计有效的控制方案实现了系统的一致性.最近,文献[13]研究了一类复杂网络的全局牵制控制问题,对于不同的网络结构,分别提出了相应的控制方案,最终实现了牵制有向复杂网络到达目标节点.在已有文献中,大多数多智能体系统的目标节点都与跟随节点保持相同的结构且是已知的.然而在实际应用中,当追踪目标比较复杂时,比如当避免危险的障碍物或跟踪所需的目标状态未知时,这类要求显得太过苛刻.因此,为了更好地切合实际,本文提出目标节点可以是未知的,通过外部的控制协议使得多智能体网络达到一致.
有限时间问题是一个非常有意义的问题.不同于渐近稳定,有限时间稳定是指能够在有限的时间内快速达到稳定,这在实际应用中有着更加广泛的应用.比如,人们需要在有限时间内接收到原始信号以及在有限时间控制器下的系统具有更好的鲁棒性和抗干扰性.近十年来,有限时间一致性问题也受到了很大的重视,并出版了一些有意义的成果[17-22].文献[22]为了实现系统的一致性,提出了两种不同的有限时间一致性协议.文献[21]通过提出双向协议的牵制方法,使复杂系统在有限时间内达到了分布式一致.在上述的大多数文献中,系统微分方程都是右端不连续的.
基于上述成果的启发,本文主要研究了在有限时间内,牵制多智能体有向网络到未知有界的目标节点问题.为了保证多智能体网络在有限时间内达到一致,本文给出了牵制控制协议,借助Lyapunov函数方法和Filippov解的相关性质,得到了网络达到一致性的充分条件.本文内容由以下几个部分组成:在第1节,给出了基本定义、引理和数学模型;第2节给出了主要定理和结论;在第3节,通过数值模拟验证了所得条件的有效性;最后,第4节给出了总结.
1 基本定义和模型
1.1 代数图理论
G(V,E,A)表示一个有向图或者无向图,其中V表示图G的点集;E⊆V ×V为图G的边集;A为权重邻接矩阵, 一个有向边〈i, j〉∈E表示节点j可以从节点i接收到信息,反之,则不可以.一个无向边〈i, j〉∈E意味着信息可以在它们之间相互传递.此外,一个图被认为是无向的,若(i,j)∈E,则(j,i)∈E.图G的邻接矩阵A=[aij] 被定义如下: 如果(j,i)∈E,那么aij>0,否则aij=0.对每个i∈V,假定aii=0.G的Laplace矩阵用L表示,其中L=[lij]N×N,lij=-aij,i≠j,和lii=∑j≠iaij,i=1,2,…,N.Ni={j∈V:(j,i)∈E}为节点i的邻点集.一条路径从智能体i1到智能体is是一组有序边,可以表示成〈ik,ik+1〉∈E,k=1,2,…,s-1.如果图中无环,则图G被认为是一个简单图,如果图中任意两个节点i和j之间存在一个从i到j的有向路径,那么就说G是强连通图.G的子图G′如果满足: 1) G′是强连通的; 2) 任何G的强连通子图无法真包含G′,则称G′是G的最大强连通子图[23].如果存在标量满足piaij=pjaji,则称此条件是细节性平衡条件,其中pi是矩阵A关于零特征值的左特征向量的分量,不失一般性令0<pi<1.
1.2 微分包含
考虑以下微分方程:
(1)
其中z∈Rn, f:Rn→Rn是一个不连续向量值函数.Filippov将方程(1)的解定义如下.
定义1[23] 一个绝对连续函数φ:[t0,t0+a]![]() Rn称为方程(1)在时间区间[t0,t0+a]上的Filippov解,如果它是如下微分包含的解:
Rn称为方程(1)在时间区间[t0,t0+a]上的Filippov解,如果它是如下微分包含的解:
K(·)表示一个集合的凸包, μ(·)表示Rn上通常的Lebesgue测度,Bδ(z)表示以z为中心、 δ为半径的开球,S表示零测度集.
设V:Rn→R是局部Lipschitz连续函数,其中V在点z沿方向ω∈Rn单侧方向的导数定义为V′(z,w)=limh→0+ (V(z+hw)-V(z))/h,V在点z沿方向ω的广义导数定义为V0(z,w)=limy→z suph→0+(V(y+hw)-V(y))/h.如果对于所有的w∈Rn,V在z点沿方向w单侧导数存在,且V′(z,w)=V0(z,w),则称函数V在点z∈Rn处是正则的.∂V(z)={limi→∞ V(zi): zi→z,zi∉ΩV∪S}是V在z处的Clarke广义梯度.其中,S是任意的零测度集,ΩV为V不可微的点集.V在z处关于式(1)的集值Lie导数定义为LfV(z)={a∈R:∃v∈K[f](z)使得a=ζ·v,∀ζ∈∂V(z)}.
V(zi): zi→z,zi∉ΩV∪S}是V在z处的Clarke广义梯度.其中,S是任意的零测度集,ΩV为V不可微的点集.V在z处关于式(1)的集值Lie导数定义为LfV(z)={a∈R:∃v∈K[f](z)使得a=ζ·v,∀ζ∈∂V(z)}.
引理1[23] 设V是Rn![]() R的一个局部Lipschitz正则函数,S是方程(1)的强不变紧集.假如对所有z∈S,max LfV(z)≤0或LfV(z)=∅,则从z0出发的任意解z(t)都收敛到包含在
R的一个局部Lipschitz正则函数,S是方程(1)的强不变紧集.假如对所有z∈S,max LfV(z)≤0或LfV(z)=∅,则从z0出发的任意解z(t)都收敛到包含在![]() 中的最大不变集M上,这里Zf,V={z∈Rn|0∈LfV(z)}.
中的最大不变集M上,这里Zf,V={z∈Rn|0∈LfV(z)}.
引理2[24] 对于非线性系统(1),假定存在一个定义在原点的邻域![]() Rn上的C1光滑的函数V(z),并且存在实数c>0和0<α<1,使得V(z)在
Rn上的C1光滑的函数V(z),并且存在实数c>0和0<α<1,使得V(z)在![]() 上正定和
上正定和![]() 在
在![]() 上半负定,则系统(1)的原点是有限时间稳定的,停息时间依赖于初始值z(0)=z0,其上界为Tz(z0)≤V(z0)1-α/(c(1-α)),其中z0为原点某一开邻域中的任何一点.如果
上半负定,则系统(1)的原点是有限时间稳定的,停息时间依赖于初始值z(0)=z0,其上界为Tz(z0)≤V(z0)1-α/(c(1-α)),其中z0为原点某一开邻域中的任何一点.如果![]() Rn并且V(z)是径向无界的(即当‖z‖→∞ 时,V(z)→∞),则系统(1)的原点是全局有限时间稳定的.
Rn并且V(z)是径向无界的(即当‖z‖→∞ 时,V(z)→∞),则系统(1)的原点是全局有限时间稳定的.
引理3[7] 图G(V,E,A)包含一个有向生成树,它的Laplace矩阵为L,则0 是L的一个特征值,且其他特征值都具有正实部.
引理4 Hölder不等式:1/p+1/q=1(p,q共轭),若f∈Lp,g∈Lq,当1≤p≤∞时,有f,g∈L1且‖fg‖L1≤‖f‖Lp‖g‖Lq.
引理5[25] 设V(z(t))在Rn→R上是连续且径向无界的函数,V(t)=V(z(t)),满足
1) V(t)=0⟹z(t)=0.
2) 如果存在ρ>0,κ>0,0<β<1,和q>1满足
或者
则
引理6[26] 令x1,x2,…,xN≥0,0<ρ≤1和![]() >1则
>1则
引理7[27] 假定Lyapunov函数V(z)定义在原点的邻域U,
则系统(1)在原点有限时间稳定.停息时间T≤ln(1-(k/α)V(z)1-p)/(k(p-1)),z∈Ω,其中Ω包含于原点的吸引域内, 且Ω={z|V(z)1-p<α/k}∩U.
引理8[28] 若图![]() 是强连通和细节性平衡的,则矩阵P(L+b)是正定的.
是强连通和细节性平衡的,则矩阵P(L+b)是正定的.
记目标节点为N+1,我们可以获得增广连通图![]() 其中点集
其中点集![]() 边集合记为
边集合记为![]() 邻接矩阵记为
邻接矩阵记为![]() 我们记
我们记![]() 的Laplace矩阵为
的Laplace矩阵为![]() 其中
其中![]() 是G的Laplace矩阵,如果i∈Vpin,则bi>0,否则bi=0.
是G的Laplace矩阵,如果i∈Vpin,则bi>0,否则bi=0.
1.3 有限时间多智能体系统的模型
考虑以下非线性多智能体系统, 每个智能体的动力学方程为
(2)
其中xi 表示第i个智能体的状态, ωi是第i个智能体的外在扰动项, ui表示系统的控制输入, f(xi,t)是一个Rn×R ![]() Rn的非线性函数.时变非线性的目标节点N+1的动力学方程被描述成如下:
Rn的非线性函数.时变非线性的目标节点N+1的动力学方程被描述成如下:
(3)
定义2 若xi(t)→xN+1(t),1≤i≤N,t→∞,则多智能体系统(2)和(3)渐近一致.如果存在一个控制协议ui 和对于任意时刻t0的初始状态x(t0),存在一个依赖于x(t0)的停息时间t*≥0,满足limt→t*‖xi(t)-xN+1(t)‖=0, xi(t)=xN+1(t),其中t≥t*,i=1,2,…,N,则多智能体有限时间一致.如果停息时间不依赖于初值x(t0),则多智能体为固定时间一致.
为了便于分析,给出如下的假设.
假设1 增广连通图![]() 包含一个以N+1为根节点的领导者和跟随者是强连通的和细节性平衡.
包含一个以N+1为根节点的领导者和跟随者是强连通的和细节性平衡.
假设2 以根节点N+1存在一条有向路径到G的外部没有连接的每个连通分量.
2 理 论 结 果
2.1 有限时间一致性分析
本小节将研究多智能体系统的有限时间一致性.跟随者在未知领导者动力学性质时,有界的非线性函数满足‖f(xi,t)-f(xN+1,t)+ωi‖∞≤d<∞,控制协议设计为
(4)
这里
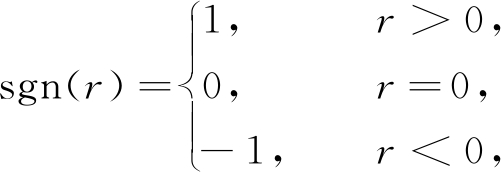
其中α为正的常数, aij为边的权重,bi为牵制增益, 本文将在Filippov意义下去理解[29].
定义全局状态向量xi(t)=(x1i,x2i,…,xni)T 和全局控制器ui=(u1i,u2i,…,uni)T. 定义误差向量:
ei=xi-xN+1, i=1,2,…,N,
则
其中
定理1 在假设1、2和牵制控制协议(4)的作用下, 若α>d,0<η<1,则多智能体系统(2)与(3)可以与有限时间达到一致.
证明 考虑如下的Lyapunov函数:
其中P=diag(p1,p2,…,pN), pi是矩阵A关于零特征值左特征向量的分量, 且0<pi≤1, 由假设1, 知![]() 是正定矩阵, 则V1正定且连续可微.V1沿着误差系统轨线的集值Lie导数为
是正定矩阵, 则V1正定且连续可微.V1沿着误差系统轨线的集值Lie导数为
令(L1⊗In)e=θ,由Hölder不等式,有
且
由引理6,得
这里PL1正定, λ1为PL1的最小特征值.基于上式和假设1, α>d>0成立, 则存在一个正数α-d=δ>0,有
LfV1(x)≤-δ(2λ1V1)1/2.
由引理2知,停息时间上界为T=V11/2(0)/(δ(2λ1)1/2).
定理1给出了多智能体系统一致性充分条件,在牵制的情形下,系统(2)和(3)以有限时间达到一致.因为有限时间一致停息时间依赖于初值.下面,我们将给出在固定时间实现一致的充分条件,并设计了新的控制协议.
注1 定理1考虑了在领导-跟随者的拓扑有向情形下(Laplace矩阵是非对称的),细节性平衡条件取代了无向图的条件.众所周知,研究有向图的协调性相比于无向图是相当的困难和有必要的.此外,定理1还给出了有向图的领导-跟随者系统在干扰的情形的协调性分析.
推论1 对于以上无向的领导-跟随者系统,在假设2和牵制控制协议(4)下,若α>d,则领导-跟随者在有限时间内达到一致.停息时间![]() 为L1的最小特征值.
为L1的最小特征值.
证明 令P=In,V1=eT(t)(L1⊗In)e(t)/2.类似于定理1的证明,可得证.
2.2 固定时间一致性
本小节将研究固定时间一致性右端不连续的多智能体系统,我们设计了新的控制协议如下:
(5)
这里sigα(r)=sgn(r)|r|α,其中实参数k1>0,q>1,bi>0.令ei(t)=xi(t)-xN+1(t),根据定理1,可得![]()
定理2 在假设1、2和牵制控制协议(5)的作用下,若α>d,多智能体系统(2)和(3)将固定时间一致,停息时间为
证明 取定理1中的V(t),计算V(t)的集值Lie导数:
类似于定理1的证明,可得
-δ(2λ1V1)1/2-k1N(1-q)/2(2λ1V1)(1+q)/2,
其中
这里(L1⊗In)e=θ.由引理6得
这里λ1为矩阵PL1的最小特征值.
推论2 对于以上无向的领导-跟随者系统,在假设1、2和牵制控制协议(5)下,若α>d,则领导-跟随者在有限时间内达到一致.
其中![]() 为L1的最小特征值.
为L1的最小特征值.
证明 令P=In,V1(t)=eT(t)(L1⊗In)e(t)/2.类似于定理2的证明,即可得证.
2.3 无扰动的有限时间一致性
假设3 存在常数γ>0,线性函数满足Lipschitz条件,即
‖f(x)-f(y)‖≤γ‖x-y‖.
我们考虑如下的多智能体系统:
(6)
控制协议设计如下:
(7)
其中 β>0, 0<η<1.
定义全局状态向量xi(t)=(x1i,x2i,…,xni)T和全局控制器ui=(u1i,u2i,…,uni)T.定义误差向量![]() 则有
则有![]()
定理3 在假设1~3和牵制控制协议(7)的作用下,若![]() 其中
其中![]() 则多智能体系统领导-跟随者可以有限时间达到一致.
则多智能体系统领导-跟随者可以有限时间达到一致.
证明 考虑如下的Lyapunov函数:
令(L1⊗In)e=θ,且
(8)
由引理6,得
这里λ1为PL1的最小特征值,
(9)
其中IⅠ={1,2,…,N},IⅡ={1,2,…,n}.由PL1为正定矩阵,同理可得
(10)
基于式(8)~(10),得
基于引理7,我们可得出多智能体系领导者和跟随者在有限时间内达到一致.停息时间为
推论3 对于以上的无向的领导-跟随者系统,在假设1~3和牵制控制协议(7)下,若![]() 其中
其中![]() 则领导-跟随者在有限时间内达到一致.
则领导-跟随者在有限时间内达到一致.
证明 令P=In,V1=eT(t)(L1⊗In)e(t)/2,类似于上述定理的证明,即可得证.
3 数 值 模 拟
考虑只有7个多智能体的无向的拓扑系统,拓扑网络如图1所示.多智能体系统(2)为
其中![]() 为领导者.系统(2)和(3)中,当ui=0时,它们为异构的动力学系统,根据假设2,选择牵制的节点为1,6,5,如图2所示(虚线为牵制边).每个智能体状态分别用xi(t)表示,每个智能体的初值分别为
为领导者.系统(2)和(3)中,当ui=0时,它们为异构的动力学系统,根据假设2,选择牵制的节点为1,6,5,如图2所示(虚线为牵制边).每个智能体状态分别用xi(t)表示,每个智能体的初值分别为
x1(0)=-0.5, x2(0)=3, x3(0)=5, x4(0)=7, x5(0)=9, x6(0)=6, x7(0)=8.
经计算![]() 由定理1,我们选择参数α=2.1,可得在t=4附近处,多智能体系统达到一致性,如图3所示.因此推论1得到验证.
由定理1,我们选择参数α=2.1,可得在t=4附近处,多智能体系统达到一致性,如图3所示.因此推论1得到验证.
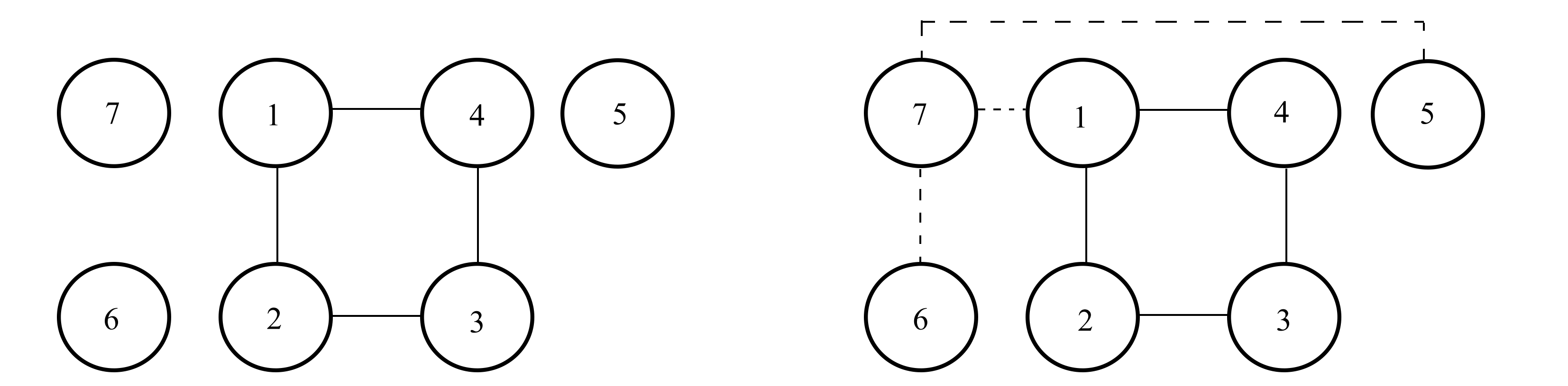
图1 图G的网络拓扑结构
Fig. 1 The network of topology G
图2 图![]() 的网络拓扑结构
的网络拓扑结构
Fig. 2 The network of topology ![]()

图3 领导者-跟随者状态的轨线
Fig. 3 The trajectory of the leader-follower state
4 结 论
本文研究了多智能体系统带扰动的有限时间及固定时间牵制一致性问题.在实际应用中,由于外界环境的干扰,领导者目标常常是未知的,我们通过有界的条件,解决了有限时间一致的问题.研究有向网络的多智能体系统是必要的和有意义的,有向网络的非线性多智能体系统有限时间同步,更贴近于实际的应用.通过有效的牵制策略,得到了使得多智能体有向网络在有限时间内及固定时间内达到一致的充分条件,数值模拟验证了本文定理的有效性.
[1] LI Z K, WEN G H, DUAN Z S, et al. Designing fully distributed consensus protocols for linear multi-agent systems with directed graphs[J]. IEEE Transactions on Automatic Control, 2015, 60(4): 1152-1157.
[2] LI Z K, REN W, LIU X D, et al. Distributed consensus of linear multi-agent systems with adaptive[J]. Automatica, 2013, 49(7): 1986-1995.
[3] LI Z K, LIU X D. Distributed tracking control for linear multiagent systems with a leader of bounded unknown input[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 518-523.
[4] LI Z K, DING Z S. Distributed adaptive consensus and output tracking of unknown linear systems on directed graphs[J]. Automatica, 2015, 55: 12-18.
[5] HONG Y G, HU J P, GAO L X. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177-1182.
[6] HONG Y G, CHEN G R, BUSHNELL L. Distributed observers design for leader-following control of multi-agent networks[J]. Automatica, 2008, 44(3): 846-850.
[7] REN W, BEARD R W, ATKINS E M. Information consensus in multivehicle cooperative control: collective group behavior through local[J]. IEEE Control Systems Magazine, 2007, 27(2): 71-82.
[8] 周军, 童东兵, 陈巧玉. 基于事件触发控制带有多时变时滞的主从系统同步[J]. 应用数学和力学, 2019, 40(12): 1389-1398. (ZHOU Jun, TONG Dongbing, CHEN Qiaoyu. Synchronization of master-slave systems with multiple time-varying delays based on the event-triggered mechanism[J]. Applied Mathematics and Mechanics, 2019, 40(12): 1389-1398. (in Chinese))
[9] ZHOU J, LU J A, LÜ J H. Pinning adaptive synchronization of a general complex dynamical network[J]. Automatica, 2008, 44(4): 996-1003.
[10] CHEN T P, LIU X W, LU W L. Pinning complex networks by a single controller[J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2007, 54(6): 1317-1326.
[11] ZHOU J, WU X Q, YU W W, et al. Pinning synchronization of delayed neural networks[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2008, 18(4): 043111.
[12] DU H B, WEN G H, WU D, et al. Distributed fixed-time consensus for nonlinear heterogeneous multi-agent systems[J]. Automatica, 2020, 113: 108797.
[13] WEN G H, YU W W, CHEN Z Q, et al. Pinning a complex network to follow a target system with predesigned control inputs[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems Digital, 2020, 50(6): 2293-2304.
[14] LÜ H, HE W L, HAN Q L, et al. Fixed-time pinning-controlled synchronization for coupled delayed neural networks with discontinuous activations[J]. Neural Networks, 2019, 116: 139-149.
[15] CHEN F, CHEN Z Z, XIANG L Y, et al. Reaching a consensus via pinning control[J]. Automatica, 2009, 45(5): 1215-1220.
[16] LIU X Y, HO D W C, SONG Q, et al. Finite/fixed-time pinning synchronization of complex networks with stochastic disturbances[J]. IEEE Transactions on Cybernetics, 2019, 49(6): 2398-2403.
[17] LI S H, DU H B, LIN X. Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics[J]. Automatica, 2011, 47(8): 1706-1712.
[18] XIAO F, WANG L, CHEN J, et al. Finite-time formation control for multi-agent systems[J]. Automatica, 2009, 45(11): 2605-2611.
[19] MENG Z Y, REN W, YOU Z. Distributed finite-time attitude containment control for multiple rigid bodies[J]. Automatica, 2010, 46(12): 2092-2099.
[20] WANG L, XIAO F. Finite-time consensus problems for networks of dynamic agents[J]. IEEE Transactions on Automatic Control, 2010, 55(4): 950-955.
[21] CORTÉS J. Finite-time convergent gradient flows with applications to network consensus[J]. Automatica, 2006, 42(11): 1993-2000.
[22] CHEN G, LEWIS F L, XIE L H. Finite-time distributed consensus via binary control protocols[J]. Automatica, 2011, 47(9): 1962-1968.
[23] 陈天平, 卢文联. 复杂网络协调性理论[M]. 北京: 高等教育出版社, 2013. (CHEN Tianping, LU Wenlian. Theory of Coordination in Complex Networks[M]. Beijing: Higher Education Press, 2013. (in Chinese))
[24] 洪奕光, 程代展. 非线性系统的分析与控制[M]. 北京: 科学出版社, 2005. (HONG Yiguang, CHENG Daizhan. Analysis and Control of Nonlinear Systems[M]. Beijing: Science Press, 2005. (in Chinese))
[25] POLYAKOV A, EFIMOV D, PERRUQUETTI W. Finite-time and fixed-time stabilization: implicit Lyapunov function approach[J]. Automatica, 2015, 51: 332-340.
[26] HARDY G, LITTLEWOOD J, P LYA G. Inequalities[M]. Cambridge: Cambridge University Press, 1952.
LYA G. Inequalities[M]. Cambridge: Cambridge University Press, 1952.
[27] SHEN Y J, XIA X H. Semi-global finite-time observers for nonlinear systems[J]. Automatica, 2008, 44(12): 3152-3156.
[28] ZHANG Y Y, YANG Y, ZHAO Y, et al. Distributed finite-time tracking control for nonlinear multi-agent systems subject to external disturbances[J]. International Journal of Control, 2013, 86(1): 29-40.
[29] FILIPPOV A F. Differential Equations With Discontinuous Right-Hand Sides[M]. Dordrecht, Netherlands: Springer, 1988.