基于比例边界有限元法和灰狼优化算法的裂纹尖端位置识别

余波; 孙文涧

doi:10.21656/1000-0887.410381

基于比例边界有限元法和灰狼优化算法的裂纹尖端位置识别

doi: 10.21656/1000-0887.410381

余波,
孙文涧

合肥工业大学土木与水利工程学院, 合肥 230009

基金项目: 国家自然科学基金(面上项目)（11872166）

详细信息

作者简介:
余波（1984—），男，副教授（通讯作者. E-mail：yubochina@hfut.edu.cn）

中图分类号: O346.1
计量
- 文章访问数: 755
- HTML全文浏览量: 289
- PDF下载量: 39
- 被引次数: 0
出版历程
- 收稿日期: 2020-12-14
- 修回日期: 2021-05-06
- 网络出版日期: 2021-12-07
- 刊出日期: 2021-11-30

Identification of Crack Tip Positions Based on the Scaled Boundary Finite Element Method and the Grey Wolf Optimization Algorithm

YU Bo,
SUN Wenjian

College of Civil Engineering, Hefei University of Technology, Hefei 230009, P.R.China

摘要

摘要: 基于比例边界有限元法(SBFEM)和灰狼优化(GWO)算法，提出了一种裂纹尖端识别方法。首先，借助SBFEM解决断裂力学问题特有的优势，快速准确地计算出反演所需的测点位移，并验证了正问题求解的正确性。其次，建立与裂纹尖端位置有关的目标函数，将求解裂纹尖端位置转换为求解目标函数最小值的优化问题。最后，采用GWO算法对目标函数进行了优化，进而搜索裂纹尖端的最佳位置。数值算例结果表明：利用SBFEM的高精度、半解析的优点，在反演过程中采用其求解正问题是非常有效的；GWO算法具有良好的全局收敛性，且相比经典的粒子群算法，能够更快速准确地搜索出裂纹尖端的位置；GWO算法具有较好的抗噪性。
- 裂纹尖端识别 /
- 比例边界有限元法 /
- 灰狼优化算法 /
- 粒子群优化算法
Abstract: Based on the scaled boundary finite element method (SBFEM) and the grey wolf optimization algorithm (GWO), an identification method for crack tips was proposed. Firstly, the special advantages of the SBFEM were used to solve the fracture mechanics problem, the displacements of measurement points required in the inversion process were quickly and accurately calculated, and the correctness of the solution to the forward problem was verified in advance. Then, the objective function related to the crack tip position was established, and the identification of the crack tip position was converted to the optimization problem of solving the minimum value of the objective function. Finally, the GWO was used to optimize the objective function, that is, to search for the optimal position of the crack tip. The numerical example results show that, it is very effective to solve forward problems in the inversion process with the high precision and semi-analytical advantages of the SBFEM. The grey wolf optimization algorithm has good global convergence property, and can search for the crack tip position more quickly and accurately compared with the classical particle swarm optimization. The grey wolf optimization algorithm has good noise resistance.
- crack tip identification /
- scaled boundary finite element method /
- grey wolf optimization algorithm /
- particle swarm optimization algorithm

HTML全文

图 1 比例边界有限单元

Figure 1. A scaled boundary finite element

下载: 全尺寸图片幻灯片

图 2 狼群社会等级

Figure 2. The social hierarchy of grey wolves

下载: 全尺寸图片幻灯片

图 3 GWO算法流程图

Figure 3. The GWO algorithm flowchart

下载: 全尺寸图片幻灯片

图 4 中心裂纹板

Figure 4. The center-cracked plate

下载: 全尺寸图片幻灯片

图 5 中心裂纹板单元划分

Figure 5. The element division of the center-cracked plate

下载: 全尺寸图片幻灯片

图 6 狼群初始位置设置

Figure 6. Initial position setting of wolves

下载: 全尺寸图片幻灯片

图 7 不同初始位置GWO算法搜索裂纹尖端的目标函数值

Figure 7. Objective function values for crack tips searched for in different initial positions with the GWO algorithm

下载: 全尺寸图片幻灯片

图 8 边缘裂纹板

Figure 8. The edge-cracked plate

下载: 全尺寸图片幻灯片

图 9 边缘裂纹板单元划分

Figure 9. The element division of the edge-cracked plate

下载: 全尺寸图片幻灯片

图 10 识别边缘裂纹尖端位置时的目标函数值

Figure 10. Objective function values for identifying the position of the edge crack tip

下载: 全尺寸图片幻灯片

图 11 斜裂纹板

Figure 11. The oblique crack plate

下载: 全尺寸图片幻灯片

图 12 迭代过程中不同的单元划分

Figure 12. Different element divisions during the iteration process

下载: 全尺寸图片幻灯片

图 13 识别斜裂纹尖端位置时的目标函数值

Figure 13. Objective function values for identifying the position of the oblique crack tip

下载: 全尺寸图片幻灯片

图 14 带裂纹扳手

Figure 14. The wrench with a crack

下载: 全尺寸图片幻灯片

图 15 带裂纹扳手的单元划分

Figure 15. The element division of the wrench with a crack

下载: 全尺寸图片幻灯片

图 16 不带误差的目标函数

Figure 16. The objective function values without measurement errors

下载: 全尺寸图片幻灯片

图 17 考虑正则化时不同测量误差的目标函数值

Figure 17. Objective function values with different measurement errors in view of the regularization scheme

下载: 全尺寸图片幻灯片

图 18 不同测量误差下目标函数值对比

Figure 18. Comparison of objective function values under different measurement errors

下载: 全尺寸图片幻灯片

表 1 中心裂纹应力强度因子

Table 1. The stress intensity factor of the center crack

SBFEM K_I / (MPa·m^1/2)	analytical solution K_I / (MPa·m^1/2)	relative error δ / %
1.4886	1.4819	0.452

下载: 导出CSV

表 2 中心裂纹尖端识别结果

Table 2. Identification results of center crack tips

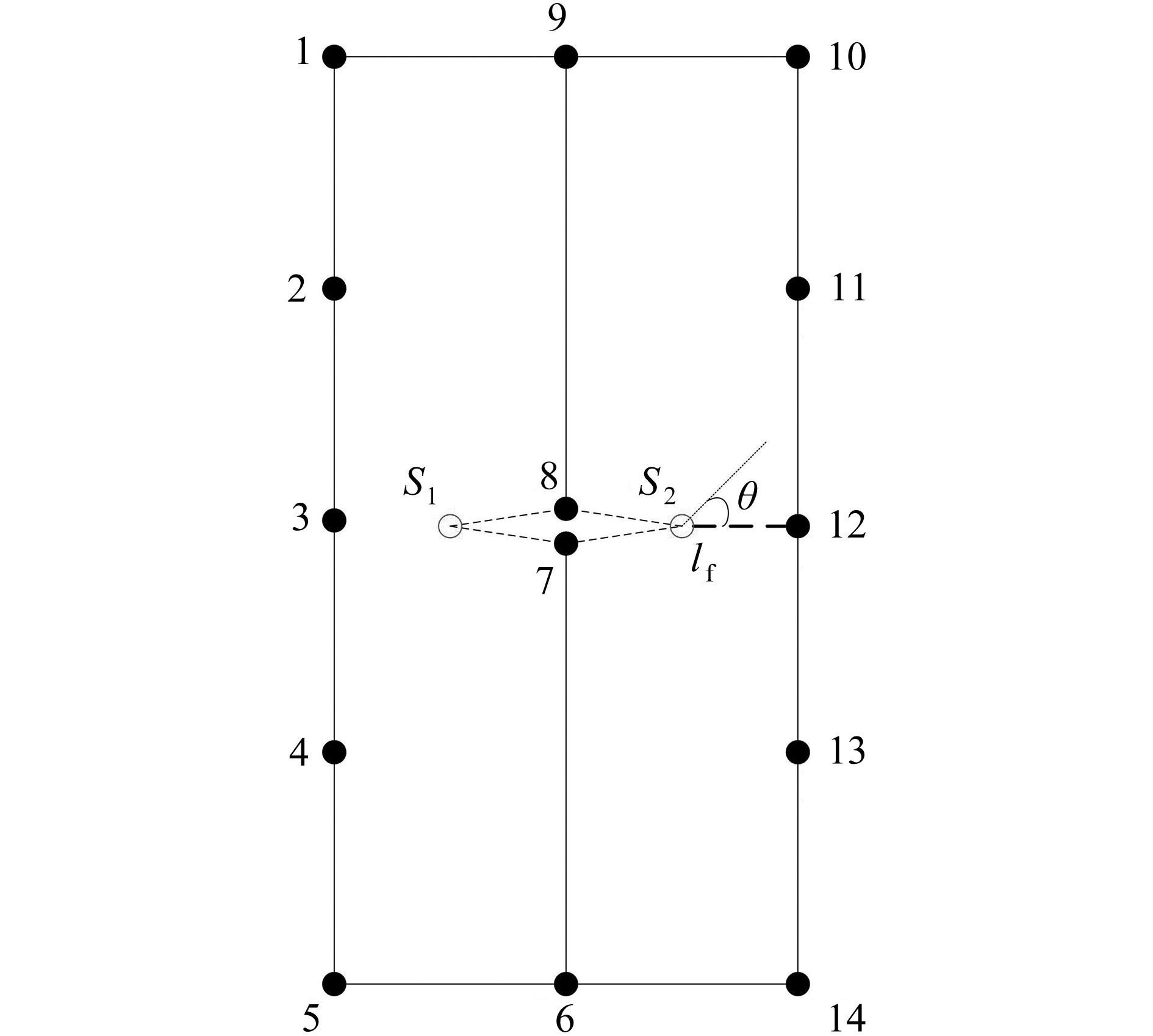
case	crack tip position (x, y) / m	objective function value
1	（−0.5001, 0.0096）,（0.4999, 0.0086）	2.49×10⁻¹³
2	（−0.5000, 0.0119）,（0.5007, 0.0273）	2.87×10⁻¹²
3	（−0.5013, 0.0419）,（0.5008, 0.0131）	6.03×10⁻¹²
4	（−0.4997, 0.0245）,（0.5003, 0.0473）	1.02×10⁻¹¹

下载: 导出CSV

表 3 GWO和PSO算法识别边缘裂纹尖端位置结果

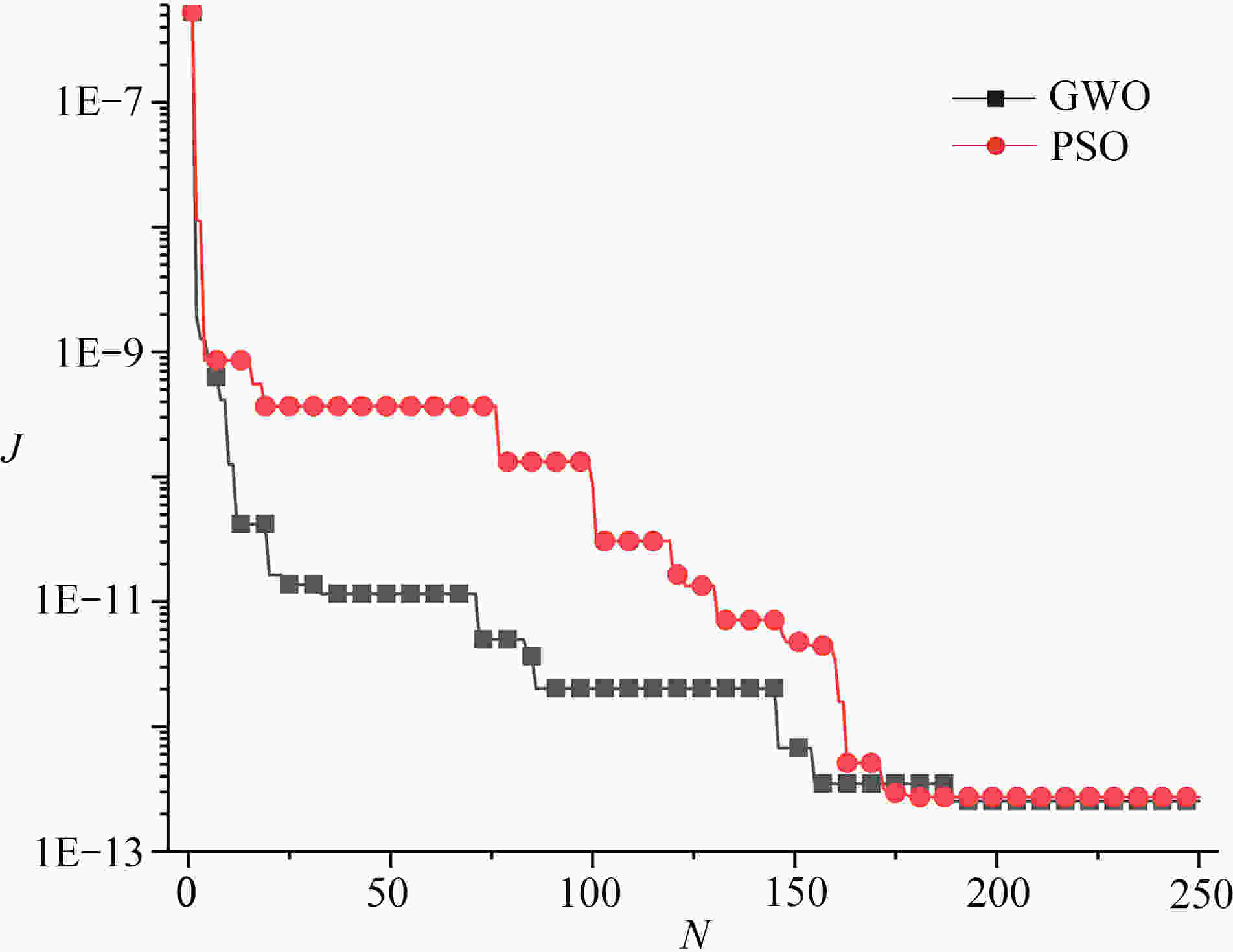
Table 3. The position of the edge crack tip identified with GWO and PSO algorithm

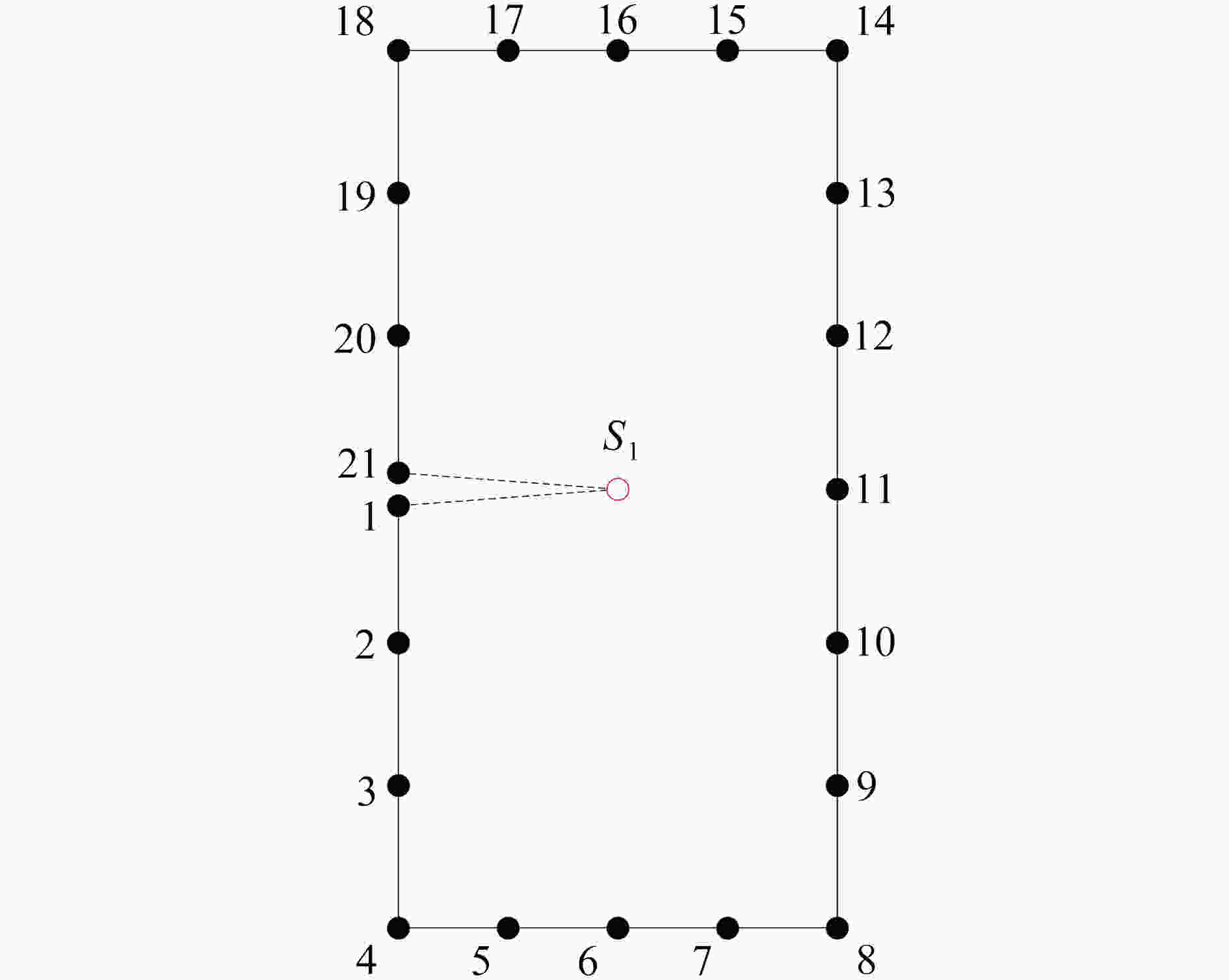
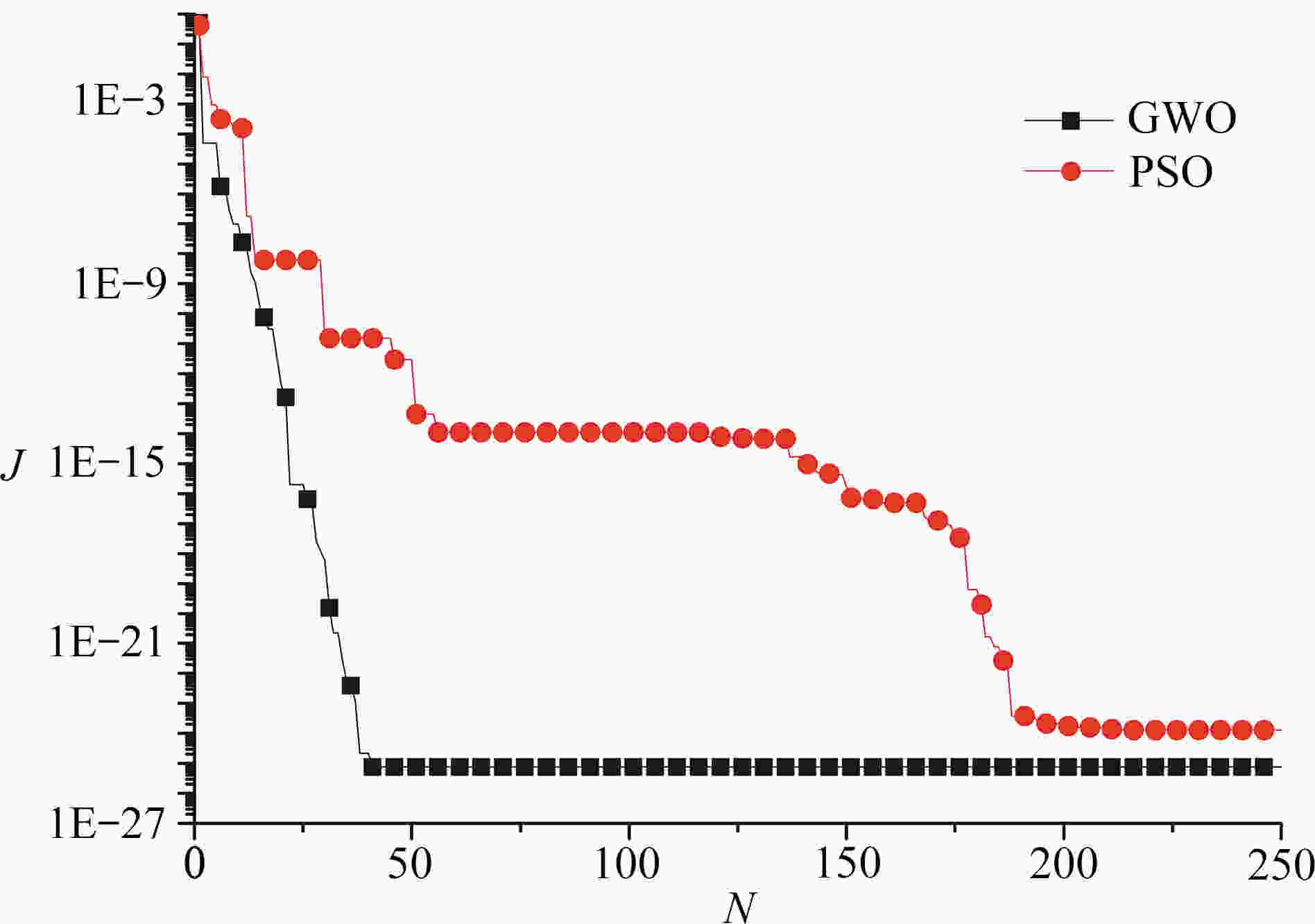
real position (x, y) / m	(x, y)_GWO / m	(x, y)_PSO / m
(0, 0)	(−1.953×10⁻¹², 3.621×10⁻¹²)	(−2.877×10⁻¹², 2.886×10⁻¹²)

下载: 导出CSV

表 4 GWO和PSO算法识别斜裂纹尖端位置

Table 4. The position of the oblique crack tips identified with GWO algorithm and PSO algorithm

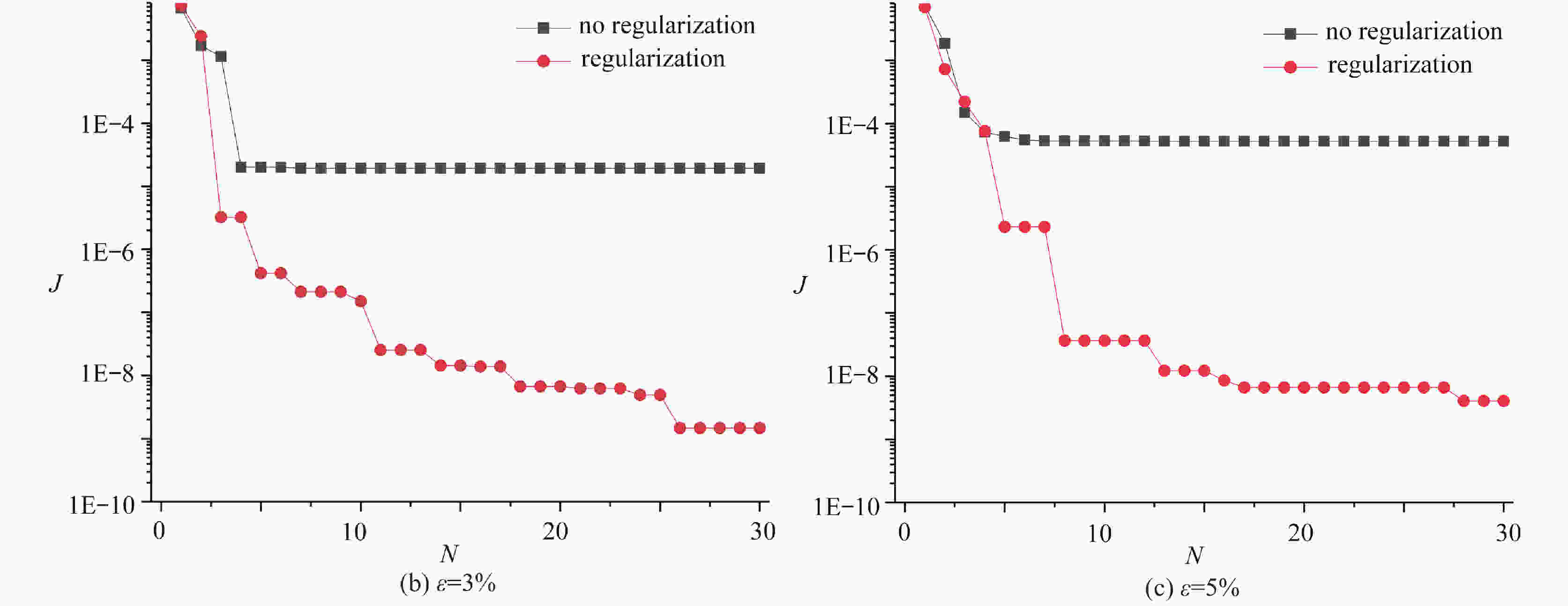
real position (x, y) / m	(x, y)_GWO / m	(x, y)_PSO / m
(−0.5, 0)	(−0.499 8, −9.2407×10⁻³)	(−0.499 8, −1.0472×10⁻³)
(0, 0.5)	(2.2318×10⁻⁴, 0.503 0)	(5.1873×10⁻⁴, 0.504 2)

下载: 导出CSV

表 5 考虑正则化时裂纹尖端识别结果

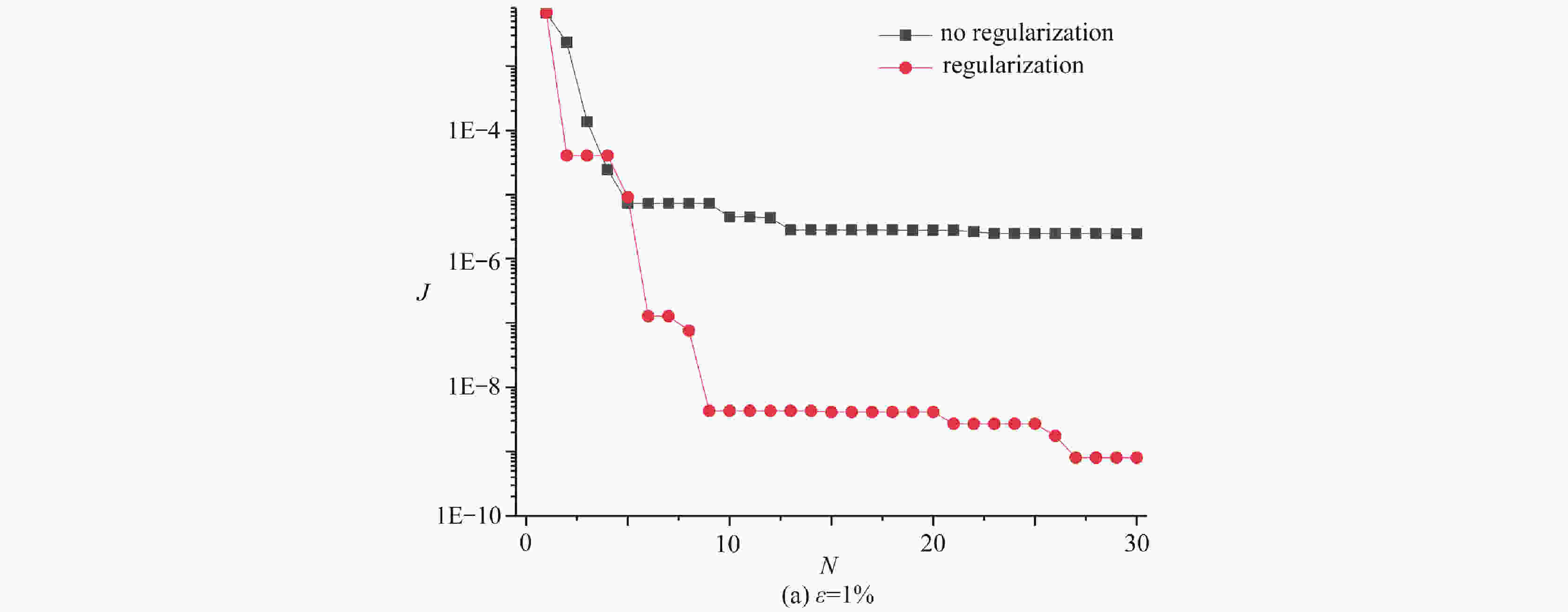
Table 5. Identification results of the crack tip in view of the regularization scheme

error ε	1%	3%	5%
objective function value of GWO result	4.537×10⁻¹³	3.153×10⁻¹²	4.109×10⁻¹¹
objective function value of PSO result	6.501×10⁻¹⁰	2.088×10⁻⁹	1.030×10⁻⁸
crack tip position of GWO result (x,y)_GWO /cm	(1.904×10⁻⁴, −4.229×10⁻⁵)	(8.294×10⁻⁴, 8.427×10⁻⁴)	(2.501×10⁻³, 5.543×10⁻⁴)
crack tip position of PSO result (x,y)_PSO /cm	(−2.713×10⁻², 5.981×10⁻³)	(−6.183×10⁻², 1.237×10⁻²)	(8.414×10⁻², −1.315×10⁻²)

下载: 导出CSV

参考文献(33)

[1]	史君林, 赵建平. 含三晶交多晶体沿晶断裂数值建模方法研究[J]. 机械强度, 2008, 40(4): 844-851. (SHI Junlin, ZHAO Jianping. Investigation on finite element modeling method of with triple junction polycrystalline intergranular fracture[J]. Journal of Mechanical Strength, 2008, 40(4): 844-851.(in Chinese)
[2]	LING X, KEANINI R G, CHERUKUR H P. A non-iterative finite element method for inverse heat conduction problems[J]. International Journal for Numerical Methods in Engineering, 2003, 56(9): 1315-1334. doi: 10.1002/nme.614
[3]	LIU J, SUN X S, HAN X, et al. A novel computational inverse technique for load identification using the shape function method of moving least square fitting[J]. Computers and Structures, 2014, 144: 127-137. doi: 10.1016/j.compstruc.2014.08.002
[4]	余波, 吴月, 聂川宝, 等. 动载荷识别的非迭代法研究[J]. 应用数学和力学, 2019, 40(5): 473-489. (YU Bo, WU Yue, NIE Chuanbao, et al. A non-iterative method for dynamic load identification[J]. Applied Mathematics and Mechanics, 2019, 40(5): 473-489.(in Chinese)
[5]	FLETCHER R, REEVES C M. Function minimization by conjugate gradients[J]. The Computer Journal, 1964, 7(2): 149-154. doi: 10.1093/comjnl/7.2.149
[6]	YANG Y C. Solving the two-dimensional inverse heat source problem through the linear least squares error method[J]. International Journal of Heat & Mass Transfer, 1998, 41(2): 393-398.
[7]	CUI M, ZHAO Y, XU B B, et al. Inverse analysis for simultaneously estimating multi-parameters of temperature-dependent thermal conductivities of an Inconel in a reusable metallic thermal protection system[J]. Applied Thermal Engineering, 2017, 125: 480-488. doi: 10.1016/j.applthermaleng.2017.06.113
[8]	UDAYRAJ, MULANI K, TALUKDAR P, et al. Performance analysis and feasibility study of ant colony optimization, particle swarm optimization and cuckoo search algorithms for inverse heat transfer problems[J]. International Journal of Heat and Mass Transfer, 2015, 89: 359-378. doi: 10.1016/j.ijheatmasstransfer.2015.05.015
[9]	BONABEAU E, DORIGO M, MARCO D R D F, et al. Swarm Intelligence: From Natural to Artificial Systems[M]. New York: Oxford University Press, 1999.
[10]	KENNEDY J, EBERHART R C. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. Piscataway, NJ, 1995.
[11]	PANDA T R, SWAMY A K. An improved artificial bee colony algorithm for pavement resurfacing problem[J]. International Journal of Pavement Research and Technology, 2018, 11(5): 509-516. doi: 10.1016/j.ijprt.2018.04.001
[12]	周焕林, 严俊, 余波, 等. 识别含热源瞬态热传导问题的热扩散系数[J]. 应用数学和力学, 2018, 39(2): 160-169. (ZHOU Huanlin, YAN Jun, YU Bo, et al. Identification of thermal diffusion coefficients for transient heat conduction problems with heat sources[J]. Applied Mathematics and Mechanics, 2018, 39(2): 160-169.(in Chinese)
[13]	LIEU Q X, LEE J. Modeling and optimization of functionally graded plates under thermo-mechanical load using isogeometric analysis and adaptive hybrid evolutionary firefly algorithm[J]. Composite Structures, 2017, 179: 89-106. doi: 10.1016/j.compstruct.2017.07.016
[14]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[15]	MIRJALILI S, SAREMI S, MIRJALILI S M, et al. Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization[J]. Expert Systems With Applications, 2016, 47: 106-119. doi: 10.1016/j.eswa.2015.10.039
[16]	OZSOYDAN F B. Effects of dominant wolves in grey wolf optimization algorithm[J]. Applied Soft Computing, 2019, 83: 105658. doi: 10.1016/j.asoc.2019.105658
[17]	NIU P, NIU S, LIU N, et al. The defect of the Grey wolf optimization algorithm and its verification method[J]. Knowledge-Based Systems, 2019, 171: 37-43. doi: 10.1016/j.knosys.2019.01.018
[18]	GILBERT S. An analysis of the finite element method[J]. Mathematics of Computation, 1974, 41(1): 115-126.
[19]	BREBBIA C A, TELLES J C F, WROBEL L C. Boundary Element Techniques: Theory and Applications in Engineering[M]. Berlin: Springer-Verlag, 1984.
[20]	郭历伦, 陈忠富, 罗景润, 等. 扩展有限元方法及应用综述[J]. 力学季刊, 2011, 32(4): 612-625. (GUO Lilun, CHEN Zhongfu, LUO Jingrun, et al. A review of the extended finite element method and its applications[J]. Chinese Quarterly of Mechanics, 2011, 32(4): 612-625.(in Chinese)
[21]	SONG C M. The Scaled Boundary Finite Element Method: Introduction to Theory and Implementation[M/OL]. Wiley Online Library, 2018(2018-06-29) [2021-05-06]. https://onlinelibrary.wiley.com/doi/book/10.1002/9781119388487.
[22]	SONG C M, WOLF J P. Semi-analytical representation of stress singularities as occurring in cracks in anisotropic multi-materials with the scaled boundary finite-element method[J]. Computers & Structures, 2002, 80(2): 183-197.
[23]	SONG C M. Evaluation of power-logarithmic singularities, T-stresses and higher order terms of in-plane singular stress fields at cracks and multi-material corners[J]. Engineering Fracture Mechanics, 2005, 72(10): 1498-1530. doi: 10.1016/j.engfracmech.2004.11.002
[24]	SONG C M. Analysis of singular stress fields at multi-material corners under thermal loading[J]. International Journal for Numerical Methods in Engineering, 2006, 65(5): 620-652. doi: 10.1002/nme.1456
[25]	DEEKS A J, CHENG L. Potential flow around obstacles using the scaled boundary finite-element method[J]. International Journal for Numerical Methods in Fluids, 2003, 41(7): 721-741. doi: 10.1002/fld.468
[26]	ANDREW J, DEEKS A J. Wave diffraction by vertical cylinder using the scaled boundary finite element method[C]//Proceeding CDROM of the Sixth World Congress on Computational Mechanics in Conjunction With the Second Asian Pacific Congress on Computational Mechanics. Beijing, China, 2004.
[27]	TAO L B, SONG H, CHAKRABARTI S. Scaled boundary FEM solution of short-crested wave diffraction by a vertical cylinder[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 197(1/4): 232-242.
[28]	SONG H, TAO L B, CHALRABARTI S. Modelling of water wave interaction with multiple cylinders of arbitrary shape[J]. Journal of Computational Physics, 2010, 229(5): 1498-1513. doi: 10.1016/j.jcp.2009.10.041
[29]	殷德胜, 尹栓, 周宜红. 裂缝分析的比例边界有限元与有限元耦合的虚拟结构面模型[J]. 计算力学学报, 2014, 31(6): 735-741, 748. (YIN Desheng, YIN Shuan, ZHOU Yihong. Coupled SBFEM and FEM for crack analysis based on virtual discontinuous surface method[J]. Chinese Journal of Computational Mechanics, 2014, 31(6): 735-741, 748.(in Chinese) doi: 10.7511/jslx201406009
[30]	YU B, HU P M, SAPUTRA A A, et al. The scaled boundary finite element method based on the hybrid quadtree mesh for solving transient heat conduction problems[J]. Applied Mathematical Modelling, 2021, 89(1): 541-571.
[31]	WOLF J P, SONG C M. The scaled boundary finite-element method, a primer: derivations[J]. Computers and Structures, 2000, 78(1/3): 191-210.
[32]	GDOUTOS E E. Fracture Mechanics: an Introduction[M]. Berlin: Springer, 2005.
[33]	CHEN H L, YU B, ZHOU H L, et al. Identification of transient boundary conditions with improved cuckoo search algorithm and polynomial approximation[J]. Engineering Analysis With Boundary Elements, 2018, 95: 124-141. doi: 10.1016/j.enganabound.2018.07.006