Determination of Soil Mechanical Parameters From Posterior Distributions Under Different Prior Distributions
-
摘要: 岩土工程中各土层参数的取值是根据现场及室内试验数据，采用经典统计学方法进行确定的，但这往往忽略了先验信息的作用。与经典统计学方法不同的是，Bayes法能从考虑先验分布的角度结合样本分布去推导后验分布，为岩土参数的取值提供一种新的分析方法。岩土工程勘察可视为对总体地层的随机抽样，当抽样完成时，样本分布密度函数是确定的，故Bayes法中的后验分布取决于先验分布，因此推导出两套不同的先验分布：利用先验信息确定先验分布及共轭先验分布。通过对先验及后验分布中超参数的计算，当样本总体符合N(μ,σ2)正态分布时，对所要研究的未知参数μ和σ展开分析，综合对比不同先验分布下后验分布的区间长度，给出岩土参数Bayes推断中最佳后验分布所要选择的先验分布。结果表明：共轭情况下的后验分布总是比无信息情况下的后验区间短，概率密度函数分布更集中，取值更方便。在正态总体情形下，根据未知参数μ和σ的联合后验分布求极值方法，确定样本总体中最大概率均值μmax和方差σmax作为工程设计采用值，为岩土参数取值方法提供了一条新的路径，有较好的工程意义。Abstract: The values of soil layer parameters in geotechnical engineering were determined according to field and laboratory test data with classical statistical methods, without use of the prior information. Unlike classical statistical methods, the Bayes method combines samples from the perspective of prior distribution to deduce the posterior distribution, providing a new analytical method for the evaluation of geotechnical parameters. The geotechnical engineering survey makes a random sampling of the overall strata. The density function of the sample distribution is determined when the sampling is completed. Therefore, the posterior distribution in the Bayes method depends on the prior distribution, and 2 different sets of prior distributions were derived: the prior distribution and the conjugate prior distribution were determined with the prior information. Through calculation of the parameters in the posterior distribution, with the sample generally conforming to the normal distribution of N(μ,σ2), unknown parameters μ and σ were analyzed, the interval lengths of the posterior distribution under different prior distributions were comprehensively compared, and the prior distribution selected for the optimal posterior distribution in the Bayes inference of the geotechnical parameter was given. The results show that, the posterior distribution in the conjugate case is always shorter than that in the absence of information, and the probability density function distribution is more centralized and the value determination is more convenient. Under the overall normal situation, the extreme value method obtained based on the joint posterior distribution of unknown parameters μ and σ to determine maximum probability mean μmax and variance σmax in the sample as the adopted values in the engineering design, provides a way for the value determination of geotechnical parameters, and has engineering significance.
-
图 1 岩土力学参数平均值μ的样本概率分布图
Figure 1. Sample probability distribution diagrams of average value μ of rock and soil mechanics parameters
图 2 岩土力学参数均值μ的1/σ的Gamma密度函数分布图
Figure 2. Gamma density function distribution diagrams of 1/σ for mean value μ of rock and soil mechanical parameters
图 3 泥炭质土c，ϕ的均值μ的后验分布概率密度曲线
Figure 3. The posterior distribution probability density curves of mean value μ of peat c and ϕ
图 5 岩土力学参数最优后验分布密度曲线
Figure 5. The optimal posterior distribution density curves of rock and soil mechanical parameters
表 1 样本矩确定先验超参数表
Table 1. Sample moment determination of prior hyper parameters
$ \theta $ [x1+xi] [xi+1+xk] [xk+1+xj] ··· [xs+1+xn] fi E F G ··· H 
下载: 导出CSV
表 2 土体c和
$ \varphi $ 原始试验样本Table 2.
The c and $ \varphi $ original samples of soilsoil name sample size N fak/ kPa index name index value 4-1 peaty soil 200 50 c/kPa 16.7, 50.6, 12.10, ···, 32.9, 28.7, 30.5, 46.4, 42.7, 3.3 200 $ \varphi /(^\circ ) $ 6.1, 3.8, 5.2, ···, 3.6, 6.9, 6.6, 6.1, 9.8, 9.8, 2.3 4-2 silty soil 190 80 c/kPa 18.5, 20.1, 20.3, 20.6, ···, 31.5, 31.8, 32.7, 34.8 190 $ \varphi /{(}^\circ ) $ 15, 15, 14, 12.3, ···, 18, 18.1, 18.4, 18.6, 18.7, 19.3 4-2 clay 210 90 c/kPa 34.44, 30.16, 28.53, 38.30,···, 29.66, 31.54, 6.64 210 $ \varphi /{(}^\circ ) $ 5.91, 5.69, 7.24, ···, 6.71, 5.10, 7.21, 5.21
下载: 导出CSV
表 3 土体力学指标分布模型选择依据
Table 3. Basis for selection of soil mechanics index distribution model
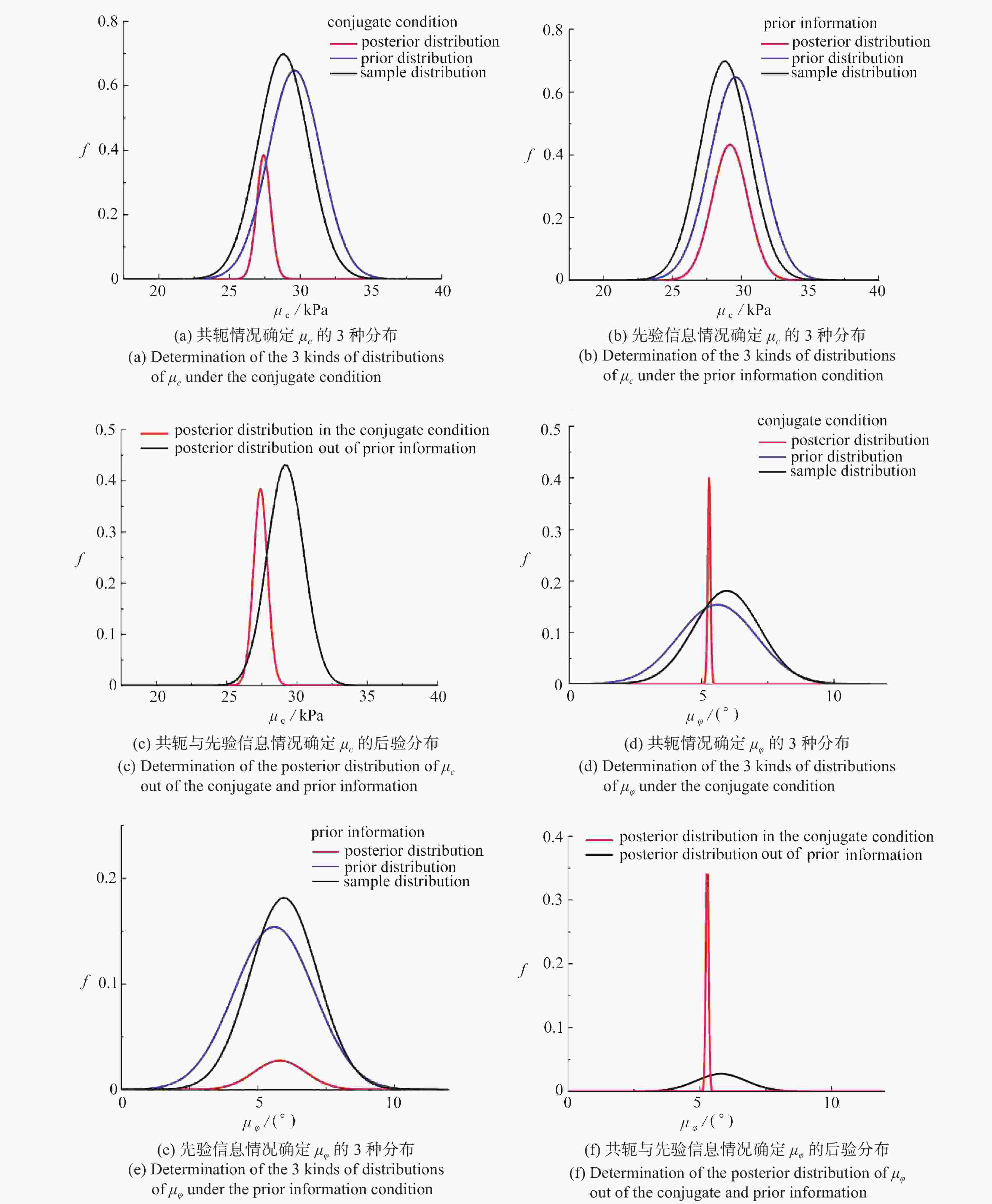
index number in fig. 1 CCV absolute value of Sk type of density function μc,ps (a) 0.232 07 0.015 89 normal distribution μϕ, ps (b) 0.216 97 0.023 64 normal distribution μc, fs (c) 0.163 66 0.016 38 normal distribution μϕ, fs (d) 0.088 32 0.022 41 normal distribution μc, c (e) 0.10 195 0.027 14 lognormal distribution μϕ, c (f) 0.099 91 0.024 58 normal distribution
下载: 导出CSV
表 4 利用先验信息计算先验及后验分布表
Table 4. Calculated prior and posterior distributions with prior information
soil name mechanical parameter $ \hat \alpha $ $ \hat \beta $ sample distribution $ f(\left. x \right|\mu ) \propto $ posterior distribution $ \pi (\left. \mu \right|x) \propto $ 4-1 peaty soil $ {\mu _{\text{c}}} $ 29.6 12.8 $ \exp \left\{ - \dfrac{{{{(x - 28.8)}^2}}}{{2 \times 10.37}}\right\} $ $ \exp \left\{ -\left (\dfrac{{{{(x - 28.8)}^2}}}{{20.74}}{\text{ + }}\dfrac{{{{(x - 29.6)}^2}}}{{25.6}}\right)\right\} $ $ {\mu _\varphi } $ 5.6 2.14 $ \exp \left\{ - \dfrac{{{{(x - 5.95)}^2}}}{{2 \times 1.54}}\right\} $ $ \exp \left\{ -\left (\dfrac{{{{(x - 5.6)}^2}}}{{4.28}}{\text{ + }}\dfrac{{{{(x - 5.95)}^2}}}{{3.08}}\right)\right\} $ 4-2 silty soil $ {\mu _{\text{c}}} $ 26.3 7.57 $ \exp \left\{ - \dfrac{{{{(x - 26.75)}^2}}}{{2 \times 5.4}}\right\} $ $ \exp \left\{ -\left (\dfrac{{{{(x - 26.75)}^2}}}{{10.8}}{\text{ + }}\dfrac{{{{(x - 26.3)}^2}}}{{15.54}}\right)\right\} $ $ {\mu _\varphi } $ 16.83 2.59 $ \exp \left\{ - \dfrac{{{{(x - 16.44)}^2}}}{{2 \times 2.4}}\right\} $ ${\rm{exp}}\left\{ {{\rm{ - }}\left( {\dfrac{{{{(x{\rm{ - 16}}.{\rm{44}})}^{\rm{2}}}}}{{{\rm{5}}.{\rm{18}}}}{\rm{ + }}\dfrac{{{{(x{\rm{ - 15}}.{\rm{9}})}^{\rm{2}}}}}{{{\rm{4}}.{\rm{8}}}}} \right)} \right\}$ 4-2 clay $ {\mu _{\text{c}}} $ 29.86 5.20 $ \exp \left\{ - \dfrac{{{{(x - 29.4)}^2}}}{{2 \times 4.5}}\right\} $ $ \exp \left\{ -\left (\dfrac{{{{(x - 29.86)}^2}}}{{10.4}}{\text{ + }}\dfrac{{{{(x - 29.4)}^2}}}{9}\right)\right\} $ $ {\mu _\varphi } $ 5.59 1.1 $ \exp \left\{ - \dfrac{{{{(x - 5.47)}^2}}}{{2 \times 0.9}}\right\} $ $ \exp \left\{ -\left (\dfrac{{{{(x - 5.59)}^2}}}{{2.2}}{\text{ + }}\dfrac{{{{(x - 5.47)}^2}}}{{1.8}}\right)\right\} $
下载: 导出CSV
表 5 共轭先验、后验分布超参数计算表
Table 5. The hyper parameter calculation table of conjugate prior and posterion distributions
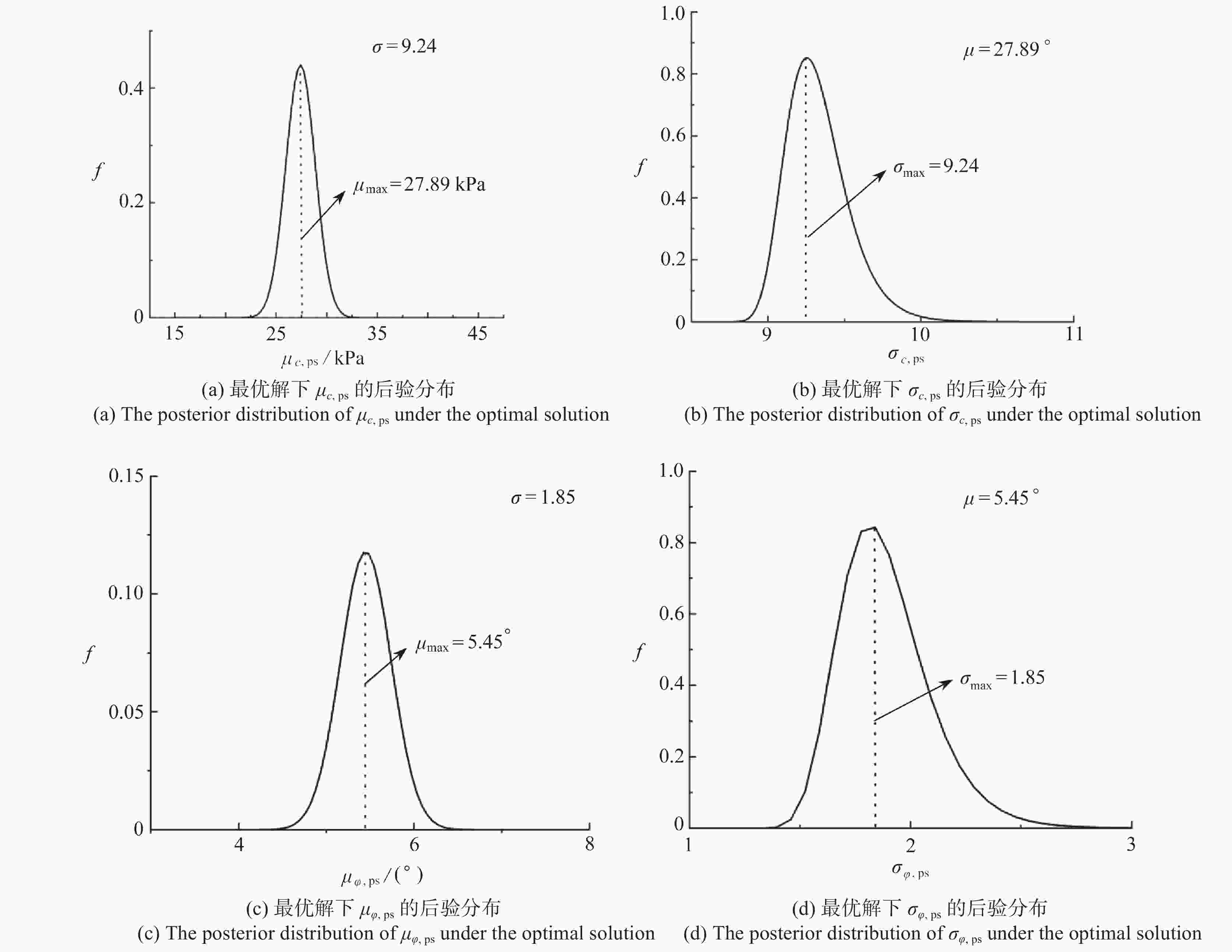
soil name index n $ \bar x $ μ S2 r ζ k kn $ \mu (\bar x) $ vn $ {\sigma _n} $ 4-1 peaty soil c 40 27.87 kPa 28.8 kPa 12.1 5.62 1.02 1.23 40.86 27.89 kPa 45.62 10.37 ϕ 40 5.44° 5.95° 2.14 7.52 4.02 0.72 40.72 5.45° 47.52 1.86 4-2 silty soil c 38 26.33 kPa 26.75 kPa 7.57 4.44 1.58 0.71 39.58 26.3 kPa 42.44 6.64 ϕ 38 16.84° 15.9° 2.58 3.86 6.26 0.93 41.86 16.8° 41.86 2.32 4-2 clay c 42 29.81 kPa 31.35 kPa 5.20 12.58 0.1 0.86 42.86 29.8 kPa 54.58 4.003 ϕ 42 5.68° 5.47° 1.1 14.84 0.54 0.82 42 .82 5.6° 56.84 0.803
下载: 导出CSV
表 6 岩土工程参数概率分布函数转化表
Table 6. The transformation table of probability distribution functions of geotechnical engineering parameters
distribution type probability density function normal distribution μ normal distribution σ normal distribution $f(x,\mu ,\sigma ) = \dfrac{1}{ {\sqrt {2{\text{π}} } \sigma } }\exp \left\{ { - \dfrac{ { { {(x - \mu )}^2} } }{ {2{\sigma ^2} } } } \right\}$ μ σ lognormal distribution $f(x,\alpha ,\gamma ) = \dfrac{1}{ {\gamma x\sqrt {2{{\text{π}} } } } }{ {\rm{exp} }{\left\{ { - { {\left( {\dfrac{ {\ln x - \alpha } }{ {2\gamma } } } \right)}^2} } \right\} } }$ $\mu = { \rm{e}^{\alpha + { {\gamma ^2} }/2 } }$ $\sigma = {\rm{e}^{2\alpha + {\gamma ^2} } }( { {{\rm{e}}^{ {r^2} } } - 1})$ Gamma distribution $f(x;r,\lambda ) = \dfrac{ { {\lambda ^r} } }{ {\Gamma (r)} }{x^{r - 1} }{\rm{e}^{ - \lambda x} }$ $\mu = \dfrac{\gamma }{\lambda }$ $\sigma = \dfrac{\gamma }{{{\lambda ^2}}}$ exponential distribution $f(x;\lambda ) = \lambda {\rm{e}^{ - \lambda x} }$ $\mu = \dfrac{1}{\lambda }$ $\sigma = \dfrac{1}{{{\lambda ^2}}}$ Beta distribution $f(x;\alpha ,\beta ) = \dfrac{{\Gamma (\alpha + \beta )}}{{\Gamma (\alpha )\Gamma (\beta )}}{x^{\alpha - 1}}{(1 - x)^{\beta - 1}}$ $\mu = \dfrac{\alpha }{{\alpha + \beta }}$ $\sigma = \dfrac{{\alpha \beta }}{{{{(\alpha + \beta )}^2}(\beta + \alpha + 1)}}$
下载: 导出CSV
-
[1] 张继周, 缪林昌. 岩土参数概率分布类型及其选择标准[J]. 岩石力学与工程学报, 2009, 28(S2): 3526-3532. (ZHANG Jizhou, MIAO Linchang. Types and selection criteria of probability distribution of rock and soil parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3526-3532.(in Chinese) [2] 宫凤强, 黄天朗, 王天成. 推断岩土参数概率分布的二维正态信息扩散法[J]. 岩石力学与工程学报, 2018, 37(10): 2232-2242. (GONG Fengqiang, HUANG Tianlang, WANG Tiancheng. A two dimensional normal information diffusion inference method for probabilistic distributions of geotechnical parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2232-2242.(in Chinese) [3] 蒋水华, 刘源, 章浩龙, 等. 先验概率分布及似然函数模型的选择对边坡可靠度评价影响的定量评估[J]. 岩土力学, 2020, 41(9): 3087-3097. (JIANG Shuihua, LIU Yuan, ZHANG Haolong, et al. Quantitatively evaluating the effects of prior probability distribution and likelihood function models on slope reliability assessment[J]. Rock and Soil Mechanics, 2020, 41(9): 3087-3097.(in Chinese) [4] 阮永芬, 高春钦, 刘克文, 等. 基于粒子群算法优化小波支持向量机的岩土力学参数反演[J]. 岩土力学, 2019, 40(9): 3662-3669. (RUAN Yongfen, GAO Chunqin, LIU Kewen, et al. Inversion of rock and soil mechanics parameters based on particle swarm optimization wavelet support vector machine[J]. Rock and Soil Mechanics, 2019, 40(9): 3662-3669.(in Chinese) [5] 黄天朗, 宫凤强, 伍婷玉. 小样本岩土参数概率分布的正交多项式推断方法[J]. 工程力学, 2017, 34(8): 85-95. (HUANG Tianlang, GONG Fengqiang, WU Tingyu. Orthogonal polynomial inference method of the probability distribution function for small samples of geotechnical parameters[J]. Engineering Mechanics, 2017, 34(8): 85-95.(in Chinese) doi: 10.6052/j.issn.1000-4750.2016.03.0169 [6] 宫凤强, 黄天朗, 李夕兵. 岩土参数最优概率分布推断方法及判别准则的研究[J]. 岩石力学与工程学报, 2016, 35(12): 2452-2460. (GONG Fengqiang, HUANG Tianlang, LI Xibing. Research on approximation method and discriminative criterion of the optimal probability distribution of geotechnical parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2452-2460.(in Chinese) [7] KRING K, CHATTERJEE S. Uncertainty quantification of structural and geotechnical parameter by geostatistical simulations applied to a stability analysis case study with limited exploration data[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 125(1): 1365-1609. [8] 吴越, 刘东升, 孙树国, 等. 岩土强度参数正态–逆伽马分布的最大后验估计[J]. 岩石力学与工程学报, 2019, 38(6): 1188-1196. (WU Yue, LIU Dongsheng, SUN Shuguo, et al. Maximum a posteriori estimation of normal inverse gamma distribution of geotechnical strength parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1188-1196.(in Chinese) [9] 阮永芬, 魏德永, 杨均, 等. 用Bayes法及后验分布极限确定土力学参数[J]. 岩土工程学报, 2020, 42(3): 438-446. (RUAN Yongfen, WEI Deyong, YANG Jun, et al. Determination of soil mechanical parameters by Bayes method and posterior distribution limit[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 438-446.(in Chinese) [10] 朱万闯, 季春霖, 邓柯. 近似Bayes计算前沿研究进展及应用[J]. 应用数学和力学, 2019, 40(11): 1179-1203. (ZHU Wanchuang, JI Chunlin, DENG Ke. Recent progress of approximate Bayesian computation and its applications[J]. Applied Mathematics and Mechanics, 2019, 40(11): 1179-1203.(in Chinese) [11] LI Z Y, WANG Y H, YANG G L. Bayesian inference of empirical coefficient for foundation settlement[J]. Journal of Southwest Jiaotong University(English Edition) , 2009, 197(1): 22-29. [12] LIN C P, HUNG Y C. Parameter estimation and uncertainty analysis incorporating engineering judgement by Bayesian inversion[C]//JUANG C H, PHOON K K, PUPPALA A J, et al. GeoRisk 2011: Geotechnical Risk Assessment and Management. 2011: 295-302. [13] STRAUB D, PAPAIOANNOU I. Bayesian updating with structural reliability methods[J]. Journal of Engineering Mechanics, 2015, 141(3): 1-13. [14] GOLLER B, BECK J L, SCHUËLLEG I, et al. Evidence-based identification of weighting factors in Bayesian model updating using modal data[J]. Journal of Engineering Mechanics, 2012, 138(5): 430-440. doi: 10.1061/(ASCE)EM.1943-7889.0000351 [15] Frank T C. On prior parameter structure investigation to parameter uncertainty[C]//American Society of Civil Engineers. World Water and Environmental Resources Congress. 2005. [16] 李书, 卓家寿, 任青文. 动力模型参数识别中的Bayes方法[J]. 应用数学和力学, 2000, 21(4): 402-408. (LI Shu, ZHUO Jiashou, REN Qingwen. Parameter identification of dynamic models using a Bayes approach[J]. Applied Mathematics and Mechanics, 2000, 21(4): 402-408.(in Chinese) doi: 10.3321/j.issn:1000-0887.2000.04.011 [17] 戴琳. 概率论与数理统计[M]. 北京: 高等教育出版社, 2011.DAI Lin. Probability Theory and Mathematical Statistics[M]. Beijing: Higher Education Press, 2011. （in Chinese） [18] 韦来生, 张伟平. Bayes分析[M]. 北京: 中国科学技术大学出版, 2013.WEI Laisheng, ZHANG Weiping. Bayes Analysis[M]. Beijing: University of Science and Technology of China, 2013. （in Chinese） [19] 刘江涛, 杨正东, 孙飞达, 等. 昆明湖相沉积软土区基坑土体抗剪强度分析研究[J]. 岩土工程学报, 2014, 36(S2): 125-129. (LIU Jiangtao, YANG Zhengdong, SUN Feida, et al. Shear strength of lacustrine deposits in soft soil area of Kunming[J]. Journal of Geotechnical Engineering, 2014, 36(S2): 125-129.(in Chinese) -
图(5) / 表(6)
计量
- 文章访问数: 766
- HTML全文浏览量: 216
- PDF下载量: 52
- 被引次数: 0
渝公网安备50010802005915号