自由漂浮空间非合作目标的运动预测

王齐帅; 周邦召; 刘晓峰; 蔡国平

doi:10.21656/1000-0887.420017

自由漂浮空间非合作目标的运动预测

doi: 10.21656/1000-0887.420017

1.
上海交通大学海洋工程国家重点实验室工程力学系，上海 200240
2.
中国工程物理研究院系统工程研究所，四川绵阳 621900

基金项目: 国家自然科学基金（11772187；11802174）；中国博士后科学基金（2018M632104）

详细信息

作者简介:
王齐帅（1992—），男，博士生（E-mail：wqs300390@sjtu.edu.cn）

蔡国平（1965—），男，教授，博士，博士生导师(通讯作者. E-mail：caigp@sjtu.edu.cn)

中图分类号: V249
计量
- 文章访问数: 726
- HTML全文浏览量: 259
- PDF下载量: 88
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-18
- 修回日期: 2021-03-16
- 网络出版日期: 2021-12-07
- 刊出日期: 2021-11-30

Motion Prediction of Free-Floating Space Non-Cooperative Targets

1.
Department of Engineering Mechanics, State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, P.R.China
2.
Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang, Sichuan 621900, P.R.China

摘要

摘要: 空间非合作目标的运动预测是航天器在轨服务中的一个重要问题。在获得非合作目标的运动预测结果后，追踪星即可规划运动轨迹以接近目标并对其进行捕获。该文提出了一种自由漂浮空间非合作目标的运动预测方法。该方法的核心思想是首先辨识出目标的姿态动力学参数和目标的质心运动学参数，然后利用参数辨识结果和目标的动力学方程实现对目标的运动预测。在姿态动力学参数的辨识过程中，首先对目标的惯性参数进行初步辨识，然后采用自适应无迹Kalman滤波器对姿态动力学参数进行粗略辨识，最后通过最优化方法进一步提高姿态动力学参数的辨识精度。该文通过数值仿真验证了所提运动预测方法的有效性。仿真结果表明，无论目标是做单轴旋转还是翻滚运动，所提运动预测方法都能够实现对目标的长时间高精度的运动预测。
- 自由漂浮空间非合作目标 /
- 运动预测 /
- 参数辨识 /
- 无迹Kalman滤波器 /
- 最优化方法
Abstract: Motion prediction of space non-cooperative target is an important issue for spacecraft on-orbit service. With obtained high-precision motion prediction results, the chaser can plan its motion trajectory to approach the target and then capture it. A motion prediction method was proposed for free-floating space non-cooperative targets. The core idea of this method is to identify kinematic parameters of the target’s mass center and attitude dynamic parameters, and then with dynamic equations for the target to realize the motion prediction. In the identification of the attitude dynamic parameters, inertia parameters of the target were preliminarily identified firstly, then an adaptive unscented Kalman filter (UKF) was used to roughly identify the attitude dynamic parameters, and finally the identification precision was further improved through optimization. In the identification of the kinematic parameters, the parameters were roughly identified firstly with the optimal attitude dynamic parameters obtained above and the kinematic equations for the target’s mass center, and then the identification precision was further improved again through optimization. In the end, the effectiveness of the proposed motion prediction method was verified by numerical simulations. Simulation results indicate that, the proposed method can achieve long-time high-precision motion prediction of the non-cooperative target whether the target is in uniaxial rotation or tumbling motion.
- free-floating space non-cooperative target /
- motion prediction /
- parameter identification /
- UKF /
- optimization

HTML全文

图 1 目标所在的坐标系

Figure 1. Coordinate systems of the target

下载: 全尺寸图片幻灯片

图 2 特征点和坐标系${\varSigma _b}$的关系

Figure 2. Feature points and frame ${\varSigma _b}$

下载: 全尺寸图片幻灯片

图 3 运动预测结果的误差

Figure 3. The errors of the predicted results

下载: 全尺寸图片幻灯片

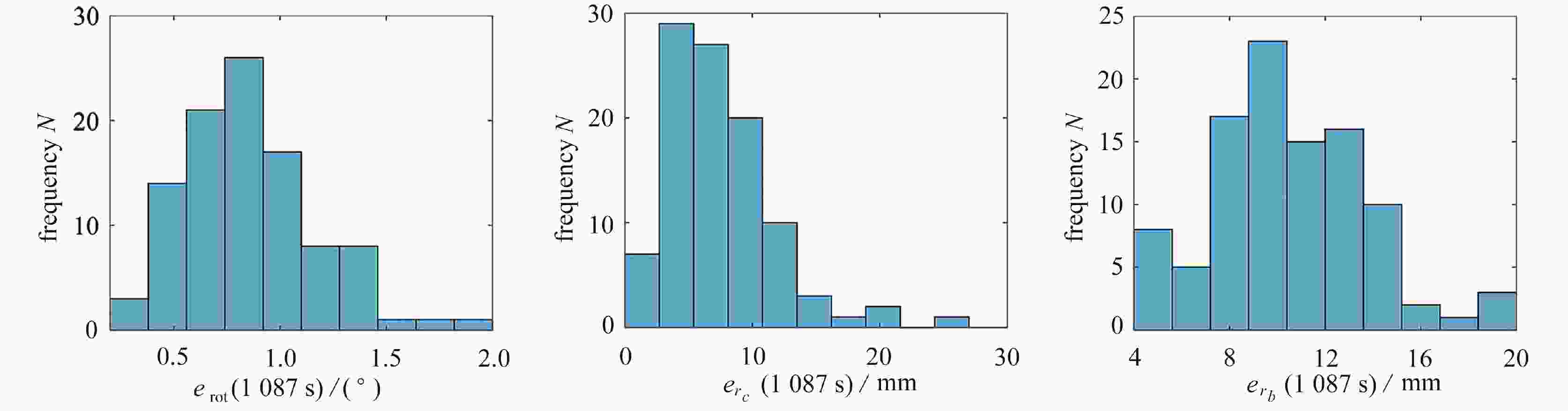
图 4 100次仿真所得$ {e_{{\rm{rot}}}}(1\;087\;{\text{s}}) $，${e_{{r_c}}}({\text{1 087}}\;{\text{s}})$和${e_{{r_b}}}({\text{1 087}}\;{\text{s}})$的频率分布直方图

Figure 4. The histograms of frequency distribution of $ {e_{{\rm{rot}}}}(1\;087\;{\text{s}}) $, ${e_{{r_c}}}({\text{1 087}}\;{\text{s}})$ and ${e_{{r_b}}}({\text{1 087}}\;{\text{s}})$ in 100 simulations

下载: 全尺寸图片幻灯片

表 1 数值仿真中参数的设置

Table 1. Setting of the parameters in the numerical simulations

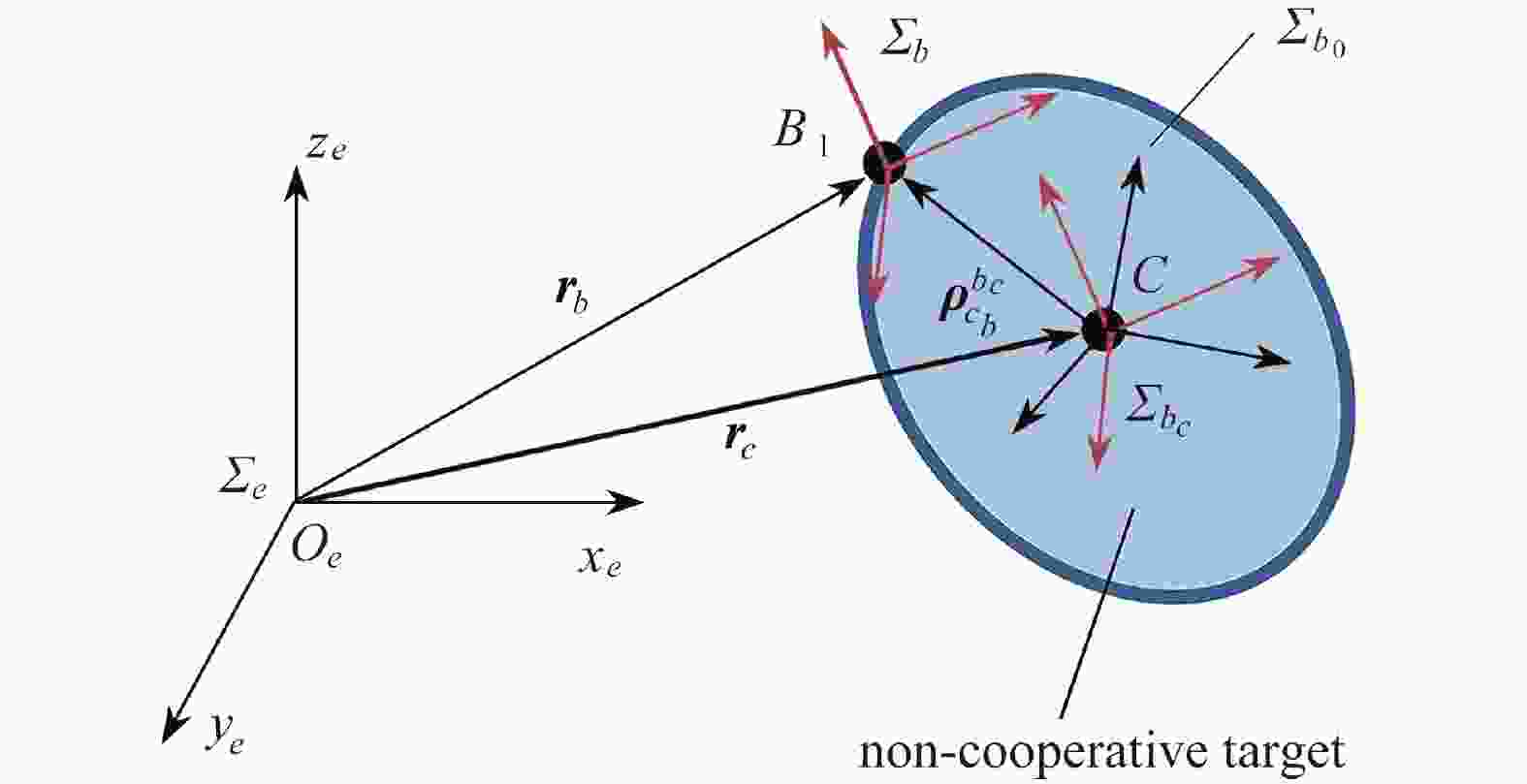
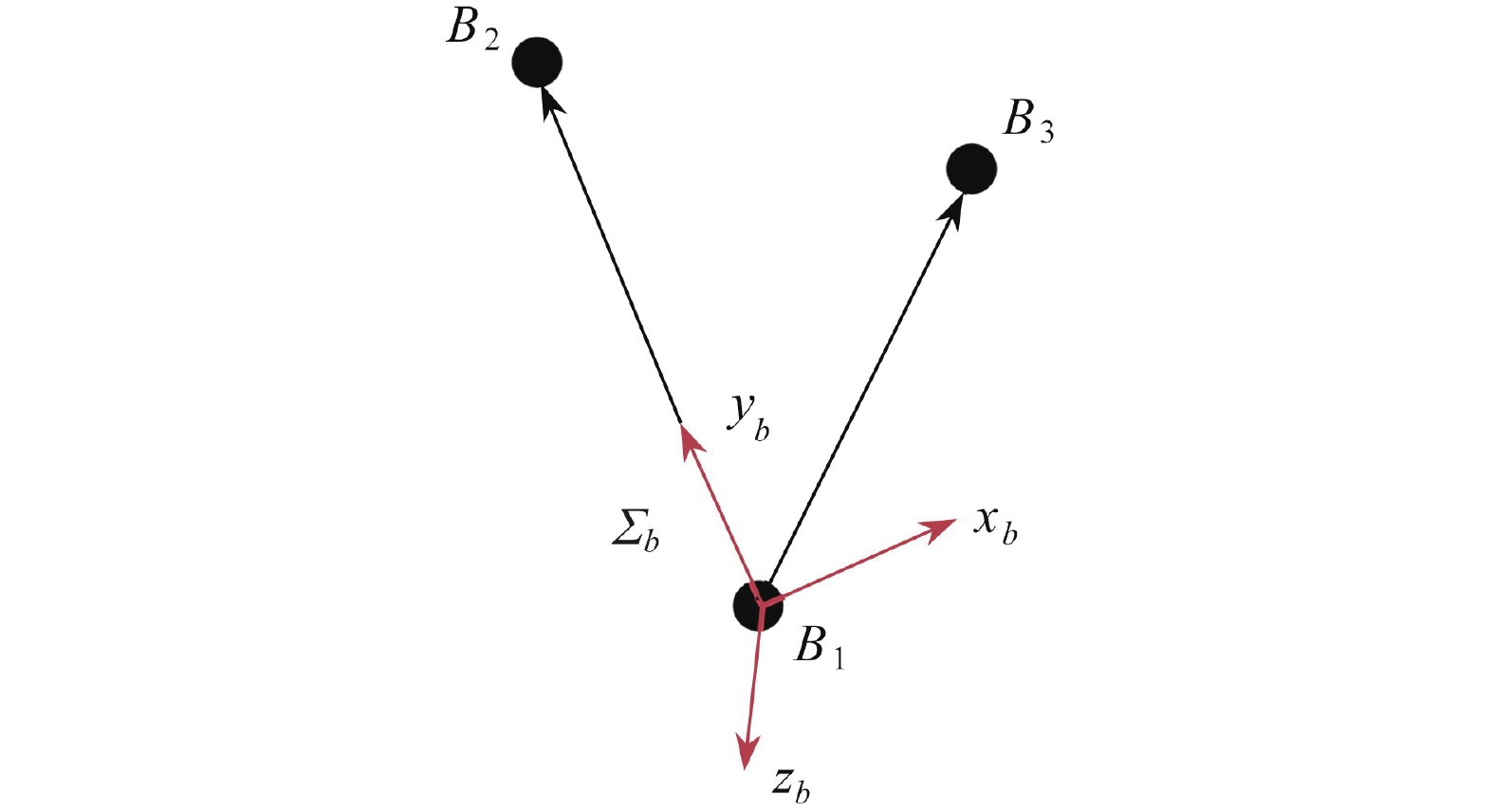
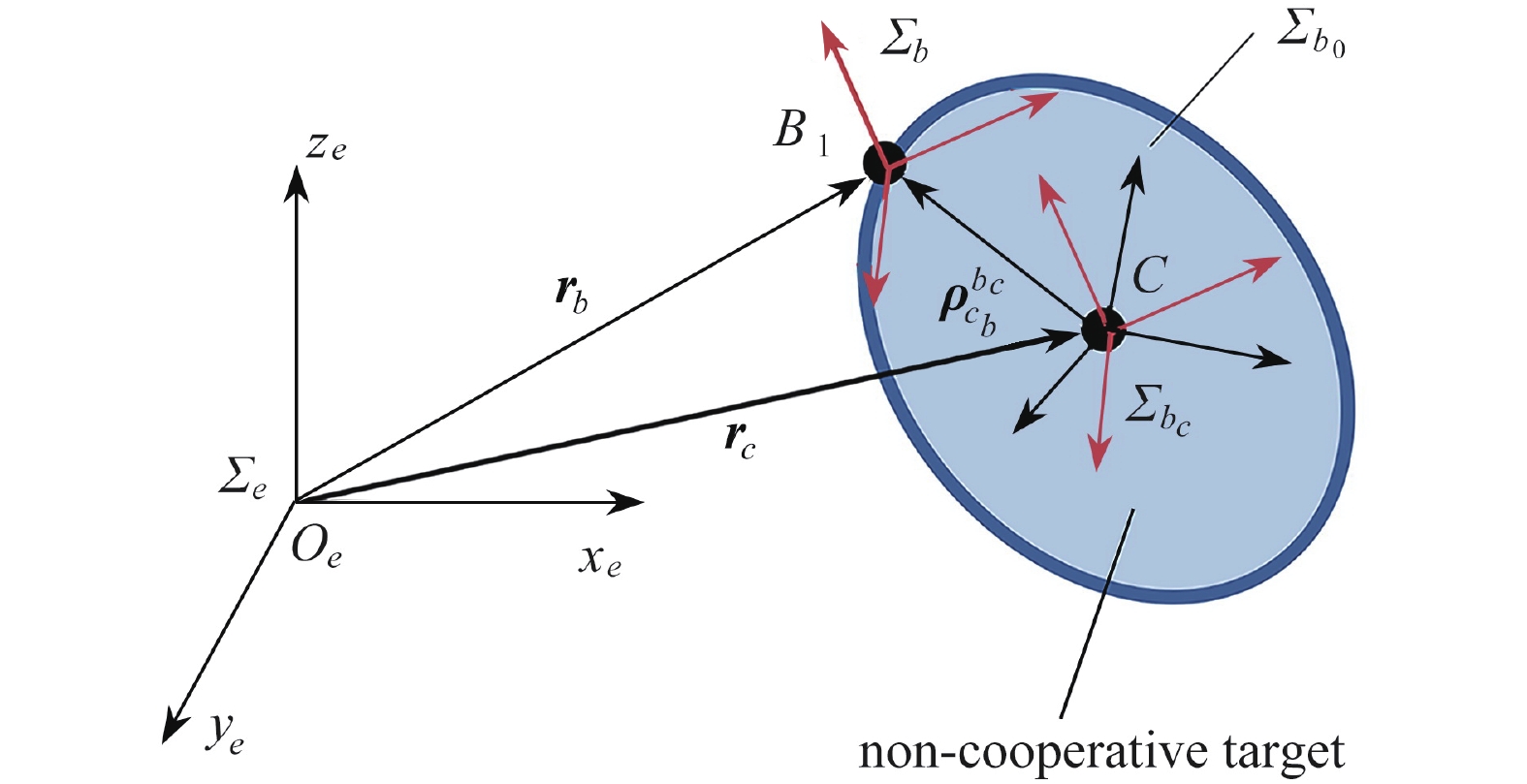
parameter	value
inertia matrix $ {{\bar{\boldsymbol{I}}}_{{b_0}}} $ of the target	$ {\rm{diag}}(1,0.8,0.52) $
rotation vector $ {{\boldsymbol{p}}_{{b_0}b}} $ from $ {\varSigma _{{b_0}}} $ to $ {\varSigma _b} $	$ {\left[ {1,\;2,\;3} \right]^{\text{T}}} $
coordinate vector $ {\boldsymbol{\rho }}_{cb}^{{b_0}} $	$ {\left[ {0.5,{\text{ 0}}{\text{.2}},{\text{ 0}}.3} \right]^{\text{T}}} $
initial angular velocity parameter $ {k_{\rm{e}}} $	$ 0,\;0.01,\;0.035,\;0.05,\;0.1,\;0.3,\;0.5,\;0.8 $
noise levels $ \left[ {{\sigma _{{\rm{tran}}}},\;{\sigma _{{\rm{rot}}}}} \right] $ (Gaussian white noise), and from small to large denoted by S, M, L and XL	$ \left[ {5\;{\text{mm}},\;1^\circ } \right] $，$ \left[ {10\;{\text{mm}},\;2^\circ } \right] $， $ \left[ {15\;{\text{mm}},\;3^\circ } \right] $，$ \left[ {20\;{\text{mm}},\;{\text{ 4}}^\circ } \right] $

下载: 导出CSV

表 2 在所有组合情况下所提运动预测方法所得的$ {t_{{\rm{val}}}} $（单位：s）

Table 2. The values of $ {t_{{\rm{val}}}} $ obtained with the proposed method under all working conditions (unit: s)

noise level	$k_{\rm{e}}$
noise level	0	0.01	0.035	0.05	0.1	0.3	0.5	0.8
S	229	2298	2054	2051	2430	2375	2296	1453
M	219	1087	936	935	1228	1075	1162	740
X	346	621	1095	1093	810	811	582	932
XL	932	933	523	621	794	703	478	296

下载: 导出CSV

表 3 在所有组合情况下所提运动预测方法所用平均观测时间$ {T_{{\rm{average}}}} $（单位：s）

Table 3. The mean observation time $ {T_{{\rm{average}}}} $ of 100 simulations obtained with the proposed method under all working conditions (unit: s)

noise level	$k_{\rm{e}}$
noise level	0	0.01	0.035	0.05	0.1	0.3	0.5	0.8
S	732.5	701.4	702.8	702.8	708.7	704.2	704.2	700
M	830.2	793.2	784.5	784.5	785.0	783.2	783.1	792.7
X	1159.7	1059.6	1046.2	1046.2	1039.2	1038.5	1038.3	1045.6
XL	1341.7	1305.1	1274.5	1274.5	1277.7	1289.6	1268.6	1277.7

下载: 导出CSV

参考文献(22)

[1]	FLORES-ABAD A, MA O, PHAM K, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68: 1-26. doi: 10.1016/j.paerosci.2014.03.002
[2]	OPROMOLLA R, FASANO G, RUFINO G, et al. A review of cooperative and uncooperative spacecraft pose determination techniques for close-proximity operations[J]. Progress in Aerospace Sciences, 2017, 93: 53-72. doi: 10.1016/j.paerosci.2017.07.001
[3]	徐方暖, 王博, 邓子辰, 等. 基于四元数方法的绳系机器人姿态控制[J]. 应用数学和力学, 2017, 38(12): 1309-1318. (XU Fangnuan, WANG Bo, DENG Zichen, et al. Attitude control of targets captured by tethered space robots based on the quaternion theory[J]. Applied Mathematics and Mechanics, 2017, 38(12): 1309-1318.(in Chinese)
[4]	王永芳, 於晓榛, 余航. 基于专利分析的自主在轨操作技术发展研究[J]. 飞行力学, 2019, 37(5): 12-17. (WANG Yongfang, YU Xiaozhen, YU Hang. Research on autonomous on-orbit operation technology development based on patent analysis[J]. Flight Dynamics, 2019, 37(5): 12-17.(in Chinese)
[5]	张治彬, 李新洪, 安继萍, 等. 一种地球静止轨道空间碎片主动清除方式[J]. 现代电子技术, 2018, 41(16): 88-91. (ZHANG Zhibin, LI Xinhong, AN Jiping, et al. An active removal method of space debris in geostationary orbit[J]. Modern Electronics Technique, 2018, 41(16): 88-91.(in Chinese)
[6]	BONNAL C, RUAULT J M, DESJEAN M C. Active debris removal: recent progress and current trends[J]. Acta Astronautica, 2013, 85: 51-60. doi: 10.1016/j.actaastro.2012.11.009
[7]	WOFFINDEN D C, GELLER D K. Navigating the road to autonomous orbital rendezvous[J]. Journal of Spacecraft and Rockets, 2007, 44(4): 898-909. doi: 10.2514/1.30734
[8]	SHARMA S, D’AMICO S. Pose estimation for non-cooperative rendezvous using neural networks[C]//AAS/AIAA Space Flight Mechanics Meeting. Maui County, Hawaii, USA, 2019.
[9]	STRUBE M, HENRY R, SKELETON E, et al. Raven: an on-orbit relative navigation demonstration using international space station visiting vehicles[C]//AAS GNC Conference. Breckenridge, CO, 2015.
[10]	HILLENBRAND U, LAMPARIELLO R. Motion and parameter estimation of a free-floating space object from range data for motion prediction[C]//8th International Symposium on Artificial Intelligence, Robotics and Automation in Space. Munich, Germany, 2005.
[11]	AGHILI F, PARSA K. Motion and parameter estimation of space objects using laser-vision data[J]. Journal of Guidance Control and Dynamics, 2009, 32(2): 537-549.
[12]	LICHTER M D, DUBOWSKY S. Estimation of state, shape, and inertial parameters of space objects from sequences of range images[C]//Proceedings of SPIE: the International Society for Optical Engineering. 2003, 5267: 194-205.
[13]	LICHTER M D, DUBOWSKY S. State, shape, and parameter estimation of space objects from range images[C]//IEEE International Conference on Robotics and Automation. New Orleans, LA, 2004.
[14]	LICHTER M D. Shape, motion, and inertial parameter estimation of space objects using teams of cooperative vision sensors[D]. PhD Thesis. Cambridge: Massachusetts Institute of Technology, 2005.
[15]	TWEDDLE B E, SAENZ-OTERO A, LEONARD J J, et al. Factor graph modeling of rigid-body dynamic for localization, mapping, and parameter estimation of a spinning object in space[J]. Journal of Field Robotics, 2015, 32(6): 897-933. doi: 10.1002/rob.21548
[16]	YUAN J P, HOU X H, SUN C, et al. Fault-tolerant pose and inertial parameters estimation of an uncooperative spacecraft based on dual vector quaternions[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2019, 233(4): 1250-1269. doi: 10.1177/0954410017751766
[17]	LI Y P, WANG Y P, XIE Y C. Using consecutive point clouds for pose and motion estimation of tumbling non-cooperative target[J]. Advances in Space Research, 2019, 63(5): 1576-1587. doi: 10.1016/j.asr.2018.11.024
[18]	MA C, DAI H H, YUAN J P. Estimation of inertial characteristics of tumbling spacecraft using constant state filter[J]. Advances in Space Research, 2017, 60(3): 513-530. doi: 10.1016/j.asr.2017.03.032
[19]	BENNINGHOFF H, BOGE T. Rendezvous involving a non-cooperative, tumbling target-estimation of moments of inertia and center of mass of an unknown target[C]//25th International Symposium on Space Flight Dynamic. München, Deutschland, 2015.
[20]	ZHOU B Z, CAI G P, LIU Y M, et al. Motion prediction of a non-cooperative space target[J]. Advances in Space Research, 2018, 61(1): 207-222. doi: 10.1016/j.asr.2017.10.028
[21]	WAN E A, VAN DER MERWE R. The Unscented Kalman Filter[M]. John Wiley & Sons Inc, 2001.
[22]	LAGARIAS J C, REEDS J A, WRIGHT M H, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions[J]. SIAM Journal of Optimization, 1998, 9(1): 112-147. doi: 10.1137/S1052623496303470