基于上限理论的孔隙水压力作用下隧道洞口段含裂缝仰坡稳定性分析

张京伍; 张海洋; 李明东; 管仲敏

doi:10.21656/1000-0887.420054

基于上限理论的孔隙水压力作用下隧道洞口段含裂缝仰坡稳定性分析

doi: 10.21656/1000-0887.420054

1.
东华理工大学土木与建筑工程学院, 南昌 330013
2.
鹏盛建设集团有限公司, 江西上饶 334600

基金项目: 国家自然科学基金 (51869001)

详细信息

作者简介:
张京伍(1985—)，男，讲师，博士，硕士生导师 (通讯作者. E-mail：zhangjingwu2010@126.com)

中图分类号: O39
计量
- 文章访问数: 823
- HTML全文浏览量: 294
- PDF下载量: 47
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-01
- 录用日期: 2021-03-01
- 修回日期: 2021-05-22
- 网络出版日期: 2021-11-15
- 刊出日期: 2021-12-01

Upper Bound Analysis on the Stability of Cracked Slopes at Tunnel Entrance Subjected to Pore Water Pressure

1.
School of Civil & Architecture Engineering, East China University of Technology, Nanchang 330013, P.R.China
2.
Pengsheng Construction Group Co. , Ltd. , Shangrao, Jiangxi 334600, P.R.China

摘要

摘要:
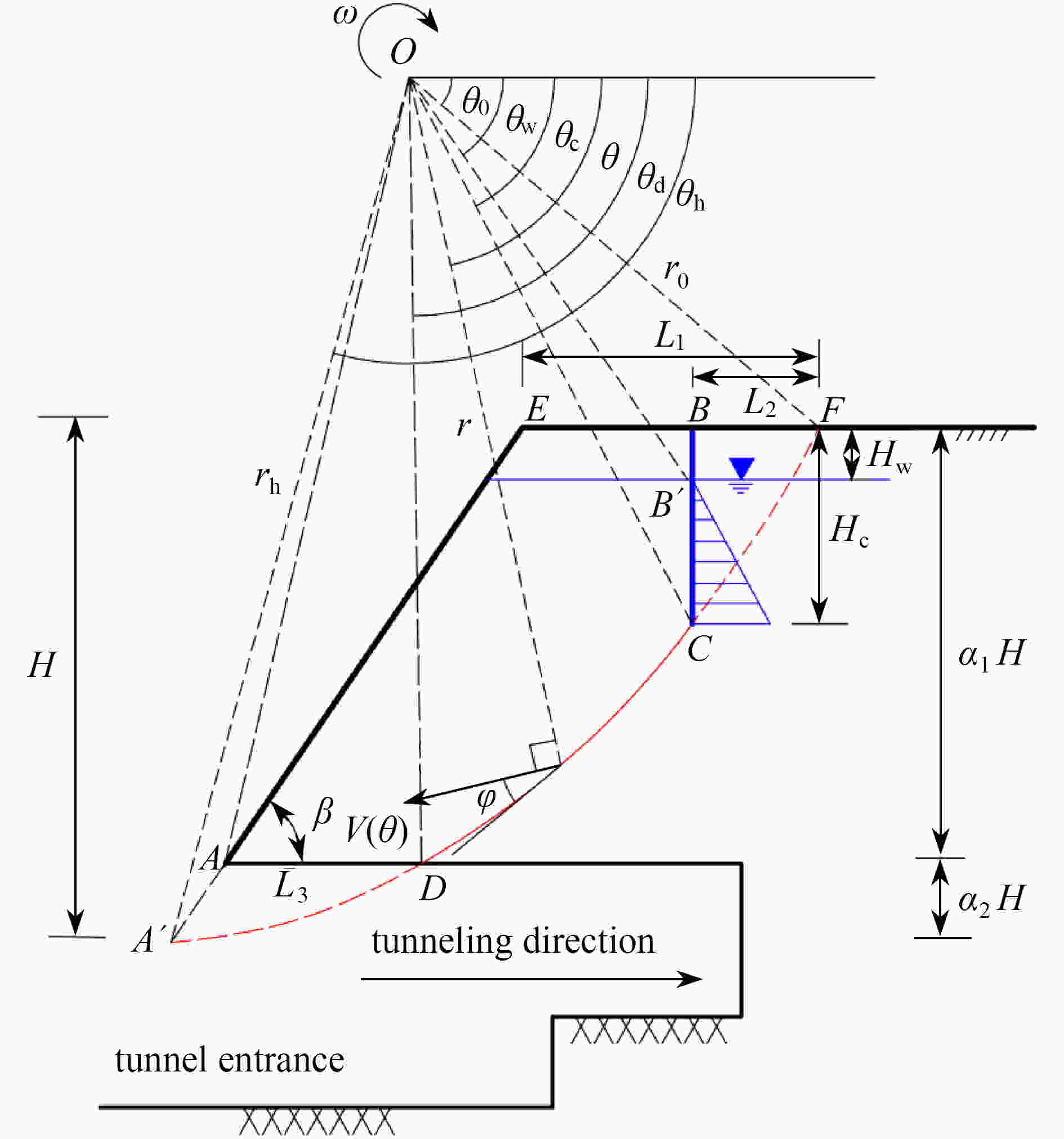
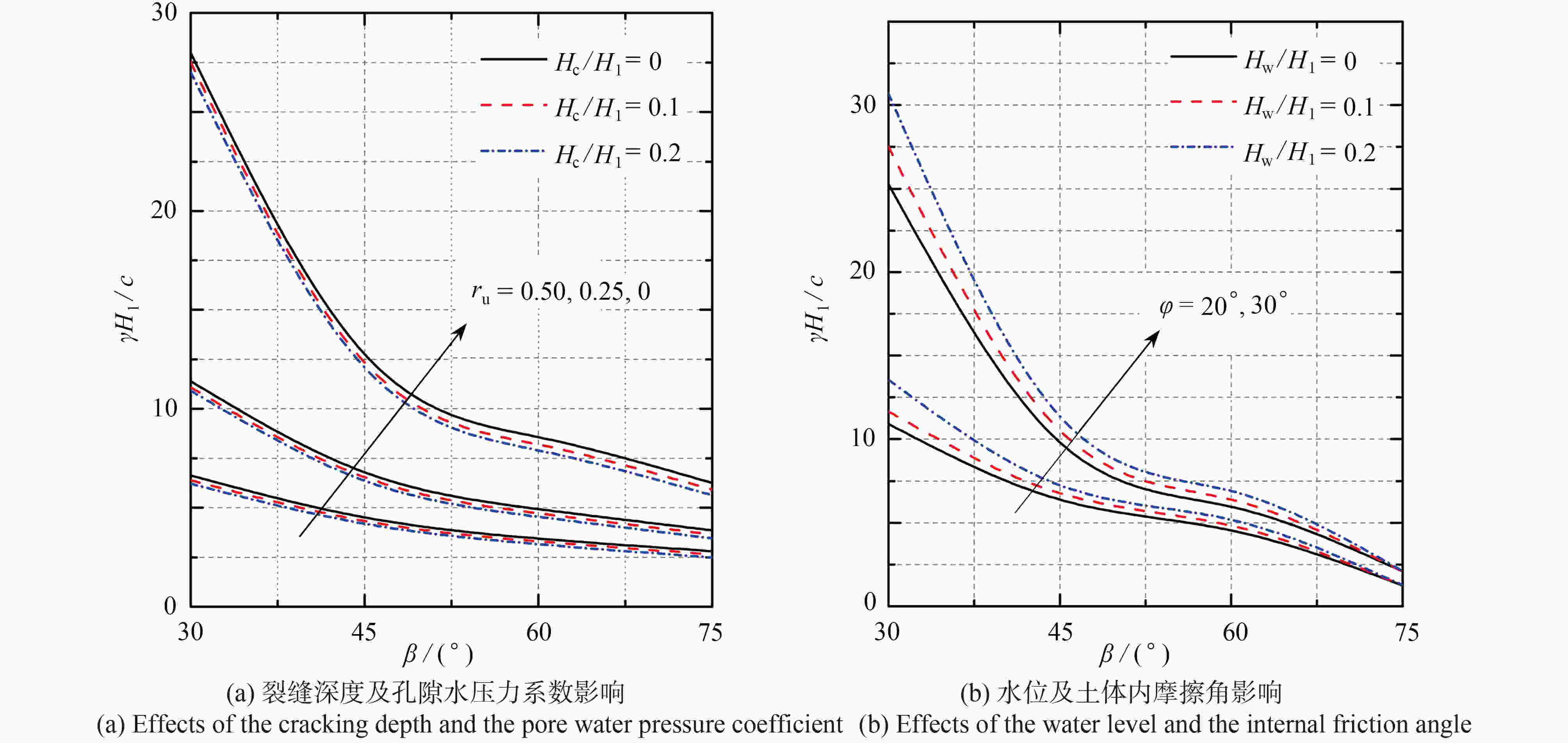
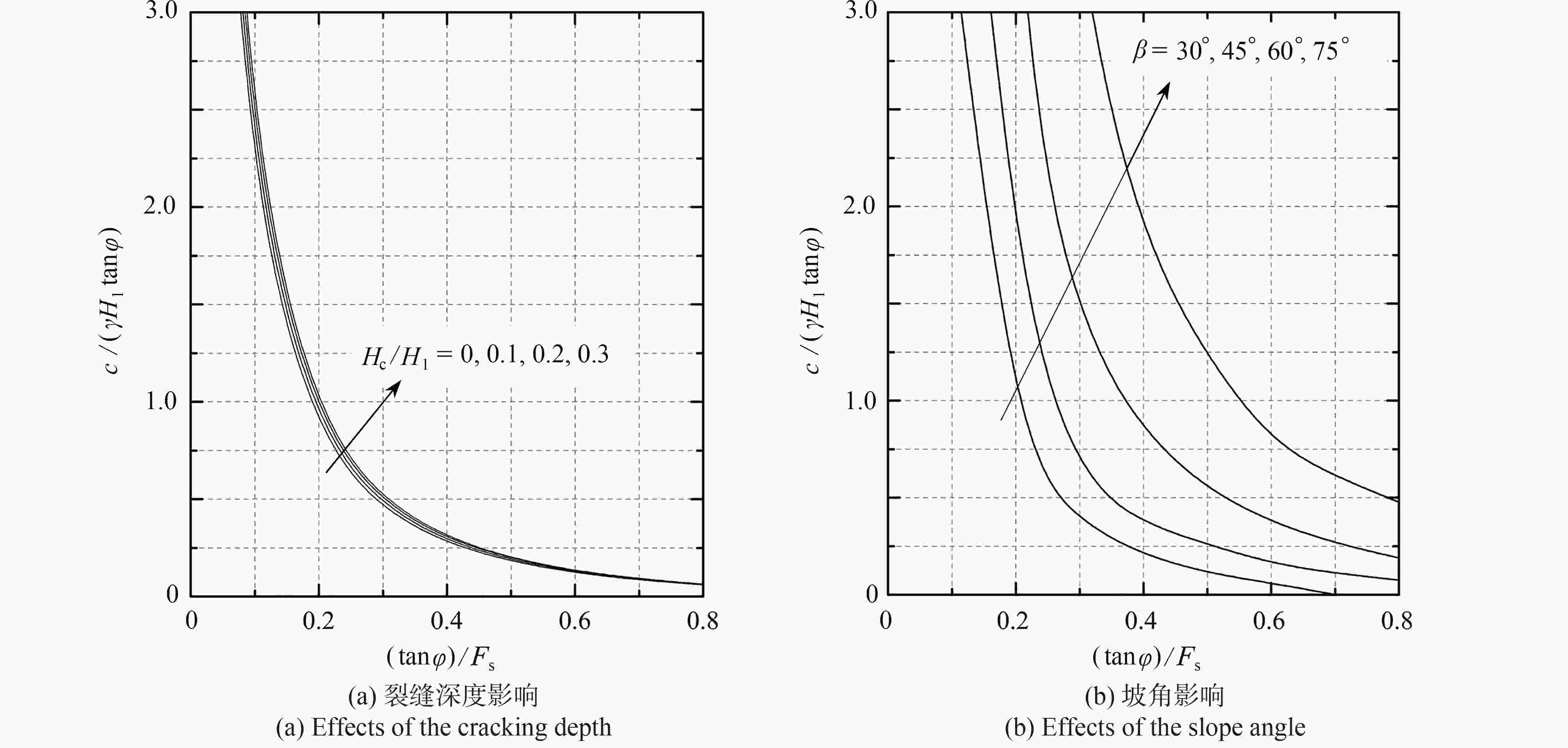
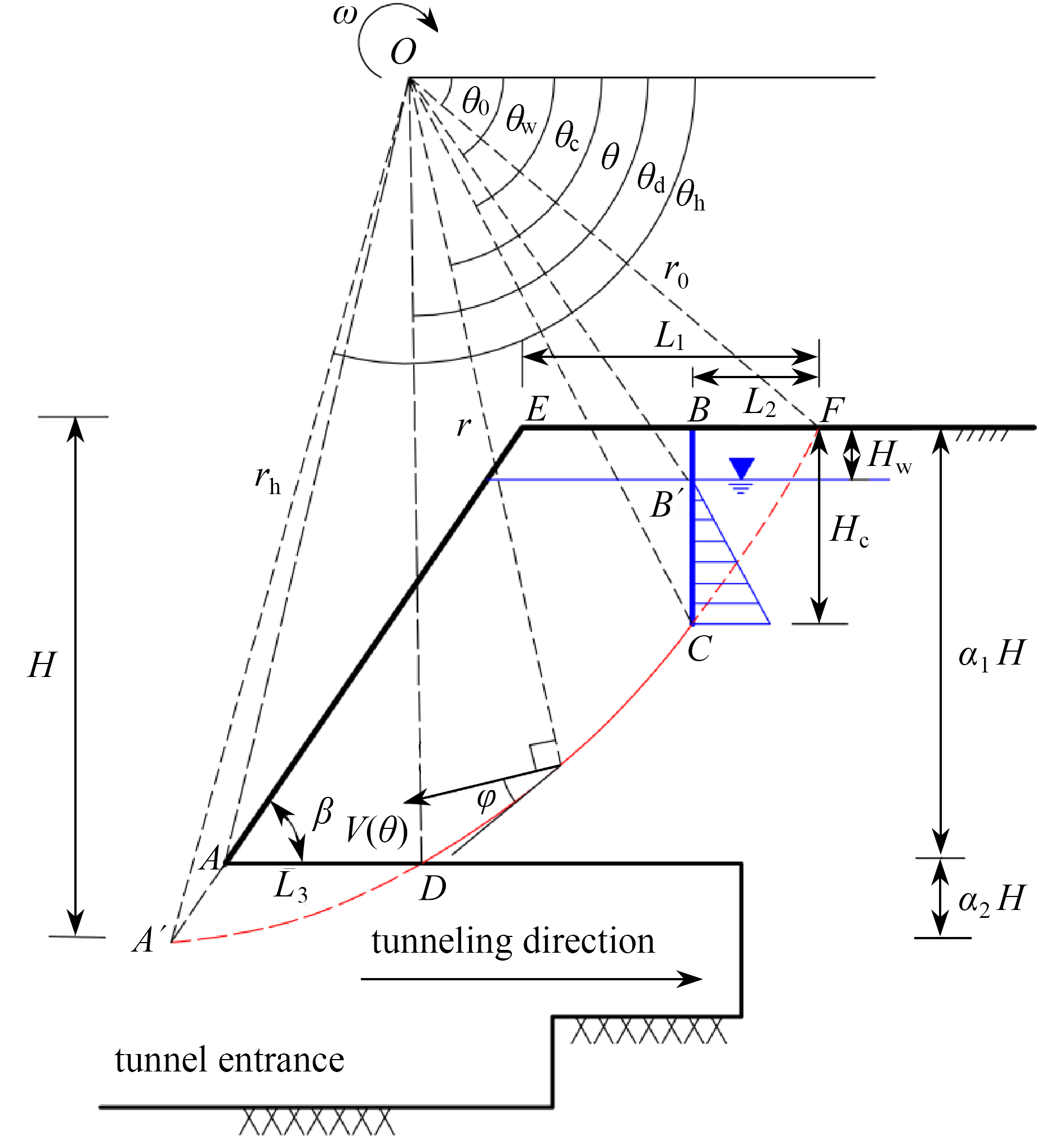
研究了孔隙水压力作用下隧道洞口段含裂缝仰坡的稳定性。采用极限分析上限法，构建了坡顶含竖向裂缝的对数螺旋转动破坏机制，推导了可反映边坡临界坡高的稳定系数计算公式，将计算结果与未考虑孔隙水压力作用下的含裂缝边坡稳定性极限分析结果进行对比，验证了所提研究方法的合理性。通过算例分析，研究了坡顶裂缝最不利位置分布及仰坡整体安全系数。结果表明：坡顶裂缝开裂深度、土体内摩擦角、坡角越大及水位分布越浅，裂缝位置越靠近坡顶边缘处；孔隙水压力系数、坡顶裂缝开裂深度越大，仰坡稳定性系数越小；坡顶裂缝越深、孔隙水压力系数越大、边坡越陡，越不利于仰坡稳定；而坡内水位分布越低，越有利于仰坡稳定。
- 极限分析上限理论 /
- 安全系数 /
- 隧道边坡 /
- 孔隙水压力 /
- 拉裂缝
Abstract:
The stability of the cracked slope at tunnel entrance subjected to pore water pressure was studied. The upper-bound limit analysis method and the logarithmic spiral rotation failure mechanism were adopted. A formula for calculating the stability coefficient reflecting the critical slope height was derived. The rationality of the proposed method was verified through comparison of the calculated results with those without effects of the pore water pressure. The distribution of the most critical crack position at the top of slope and the safety factor of the slope were studied by an example analysis. The results show that, the greater the crack depth is, the larger the internal friction angle and the slope angle will be, and the shallower the water level is, the closer the crack position will be to the edge of the slope. The greater the pore water pressure coefficient and the cracking depth are, the smaller the stability coefficient of the slope top will be. The deeper the crack is, the higher the pore water pressure coefficient and the steeper the slope will be, and the more unstable the slope will be. However, the lower the water level is, the more stable the slope will be.
- upper bound theorem of limit analysis /
- safety factor /
- slope at tunnel entrance /
- pore-water pressure /
- tensile crack

HTML全文

图 1 孔隙水压力作用下隧道洞口段含裂缝仰坡破坏机制

Figure 1. The failure mechanism for a cracked slope at tunnel entrance subjected to pore water pressure

下载: 全尺寸图片幻灯片

图 2 含裂缝边坡稳定性系数计算结果对比

Figure 2. Comparisons of stability factors of the cracked slope

下载: 全尺寸图片幻灯片

图 3 不同参数对坡顶裂缝位置分布影响规律

Figure 3. Influence of different parameters on critical position of cracks

下载: 全尺寸图片幻灯片

图 4 不同参数对裂缝边坡稳定性系数的影响规律

Figure 4. Influence of different parameters on stability factors of cracked slope

下载: 全尺寸图片幻灯片

图 5 隧道洞口段含裂缝仰坡稳定图

Figure 5. Stability of the cracked slope at tunnel entrance

下载: 全尺寸图片幻灯片

图 6 隧道洞口段含裂缝仰坡安全系数

Figure 6. Safety factors of cracked slope at tunnel entrance

下载: 全尺寸图片幻灯片

参考文献(23)

[1]	李小青. 隧道工程[M]. 1版. 北京: 中国建筑工业出版社, 2010. LI Xiaoqing. Tunnel Engineering[M]. 1st ed. Beijing: China Architecture and Building Press, 2010. （in Chinese）
[2]	于宁, 朱合华, 苏生瑞. 大风垭口公路隧道施工中的地质灾害及对策[J]. 地质灾害与环境保护, 2003, 14(2): 21-26. (YU Ning, ZHU Hehua, SU Shengrui. Analysis of geological hazards and corresponding management during the road construction[J]. Journal of Geological Hazards and Environment Preservation, 2003, 14(2): 21-26.(in Chinese) doi: 10.3969/j.issn.1006-4362.2003.02.005
[3]	邹飞, 程肖, 赵炼恒, 等. 水力效应对裂缝边坡稳定性影响的上限分析[J]. 北京工业大学学报, 2016, 42(12): 104-112. (ZOU Fei, CHENG Xiao, ZHAO Lianheng, et al. Upper bound analysis of cracked slopes subject to hydraulic effect[J]. Journal of Beijing University of Technology, 2016, 42(12): 104-112.(in Chinese)
[4]	TERZAGHI K, PECK R B. Soil Mechanics in Engineering Practice[M]. New York: John Wiley and Sons, 1967.
[5]	SPENCER E. Amethod of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11-26.
[6]	LAW K T, LUMB P. A limit equilibrium analysis of progressive failure in the stability of slopes[J]. Canadian Geotechnical Journal, 1978, 15(1): 113-122. doi: 10.1139/t78-009
[7]	ZHU D Y, LEE C F, JIANG H D. Generalised framework of limit equilibrium methods for slope stability analysis[J]. Géotechnique, 2003, 53(4): 377-395.
[8]	BAKER R. Tensile strength, tension cracks, and stability of slopes[J]. Soils and Foundations, 1981, 21(2): 1-17. doi: 10.3208/sandf1972.21.2_1
[9]	LESHCHINSKY D. Slope stability analysis: generalized approach[J]. Journal of Geotechnical Engineering, 1990, 116(5): 851-867. doi: 10.1061/(ASCE)0733-9410(1990)116:5(851)
[10]	ANTÃO A N, GUERRA N M D C, MATOS FERNANDES M, et al. Influence of tension cut-off on the stability of anchored concrete soldier-pile walls in clay[J]. Canadian Geotechnical Journal, 2008, 45(7): 1036-1044. doi: 10.1139/T08-039
[11]	LIU F T, ZHAO J D. Limit analysis of slope stability by rigid finite-element method and linear programming considering rotational failure[J]. International Journal of Geomechanics, 2013, 13(6): 827-839. doi: 10.1061/(ASCE)GM.1943-5622.0000283
[12]	CHEN W F. Limit Analysis and Soil Plasticity[M]. New York: Elsevier Scientific Publishing Company, 1975.
[13]	DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis or limit design[J]. Quarterly of Applied Mathematics, 1952, 10(2): 157-164. doi: 10.1090/qam/48291
[14]	赵炼恒, 罗强, 李亮, 等. 水平矩形浅锚极限抗拔力分析[J]. 岩土工程学报, 2009, 32(9): 1414-1420. (ZHAO Lianheng, LUO Qiang, LI Liang, et al. Ultimate pullout capacity of horizontal rectangular plate anchors[J]. Chinese Journal of Geotechnical Engineering, 2009, 32(9): 1414-1420.(in Chinese) doi: 10.3321/j.issn:1000-4548.2009.09.015
[15]	MICHALOWSKI R L. Limit loads on reinforced foundation soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(4): 381-390. doi: 10.1061/(ASCE)1090-0241(2004)130:4(381)
[16]	LI Y, EMERIAULT F, KASTNER R, et al. Stability analysis of large slurry shield-driven tunnel in soft clay[J]. Tunnellingand Underground Space Technology, 2009, 24(4): 472-481. doi: 10.1016/j.tust.2008.10.007
[17]	杨峰, 阳军生, 张学民, 等. 斜坡地基单侧滑移破坏模式及承载力上限解[J]. 工程力学, 2010, 27(6): 162-168. (YANG Feng, YANG Junsheng, ZHANG Xuemin, et al. One-side slip failure mechanism and upper bound solution forbearing capacity of foundation on slope[J]. Engineering Mechanics, 2010, 27(6): 162-168.(in Chinese)
[18]	张翔, 李林安, 王世斌, 等. 考虑底部隆起的浅埋隧道围岩压力计算分析[J]. 应用数学和力学, 2017, 38(8): 911-921. (ZHANG Xiang, LI Lin’an, WANG Shibin, et al. Limit analysis of surrounding rock pressure for shallow tunnels considering floor heave[J]. Applied Mathematics and Mechanics, 2017, 38(8): 911-921.(in Chinese)
[19]	MICHALOWSKI R L. Slope stability analysis: a kinematical approach[J]. Géotechnique, 1995, 45(2): 283-293.
[20]	VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown[J]. Canadian Geotechnical Journal, 2006, 43(8): 802-814. doi: 10.1139/t06-042
[21]	UTILI S. Investigation by limit analysis on the stability of slopes with cracks[J]. Géotechnique, 2013, 63(2): 140-154.
[22]	刘锋, 芮勇勤, 张春. 坡顶张拉裂缝对边坡稳定性影响[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35(9): 949-954. (LIU Feng, RUI Yongqin, ZHANG Chun. Influence of tension cracks of slope crest on the stability of slope[J]. Journal of Liaoning Technical University(Natural Science Edition), 2016, 35(9): 949-954.(in Chinese) doi: 10.11956/j.issn.1008-0562.2016.09.010
[23]	BISHOP A W, MORGENSTERN N R. Stability coefficients forearth slopes[J]. Géotechnique, 1960, 10(4): 129-153.