A Rotated Mixed Scheme for Solving 2D Shallow Water Equations
-
摘要:
针对二维浅水波方程数值求解问题，构造了一种旋转通量混合格式。空间方向上，该算法利用浅水波方程通量函数的旋转不变性，在单元界面法线方向及单元界面切线方向上采用可消除红斑现象的HLL与满足热力学第二定律的熵稳定加权混合数值通量函数，时间方向上采用三阶强稳定Runge-Kutta法。数值结果表明，该混合格式对于二维浅水波方程数值求解具有分辨率高的良好特性。
-
关键词:
- 旋转不变性 /
- 熵稳定格式 /
- HLL格式 /
- 有限体积法 /
- Runge-Kutta 法
Abstract:A rotated flux mixed scheme was proposed for solving 2D shallow water equations. Spatially, the algorithm uses the rotation invariance of the shallow water equations. In the normal direction and tangent direction of the element interface, both the HLL, which can eliminate the carbuncle, and the entropy stable weighted hybrid numerical flux function satisfying the 2nd law of thermodynamics, were applied to give fine numerical results. Temporally, the 3rd-order strongly stable Runge-Kutta method was used. The numerical results show that, the new scheme has high resolution for solving 2D shallow water equations.
-
Key words:
- rotation invariance /
- entropy stable scheme /
- HLL scheme /
- finite-volume method /
- Runge-Kutta method
-
图 2 二维圆柱溃坝问题密度等值线图：(a) 非混合格式密度结果；(b) 混合格式密度结果
Figure 2. The density contour for the 2D cylindrical dam-break problem：(a) the non-mixed scheme density results; (b) the mixed scheme density results
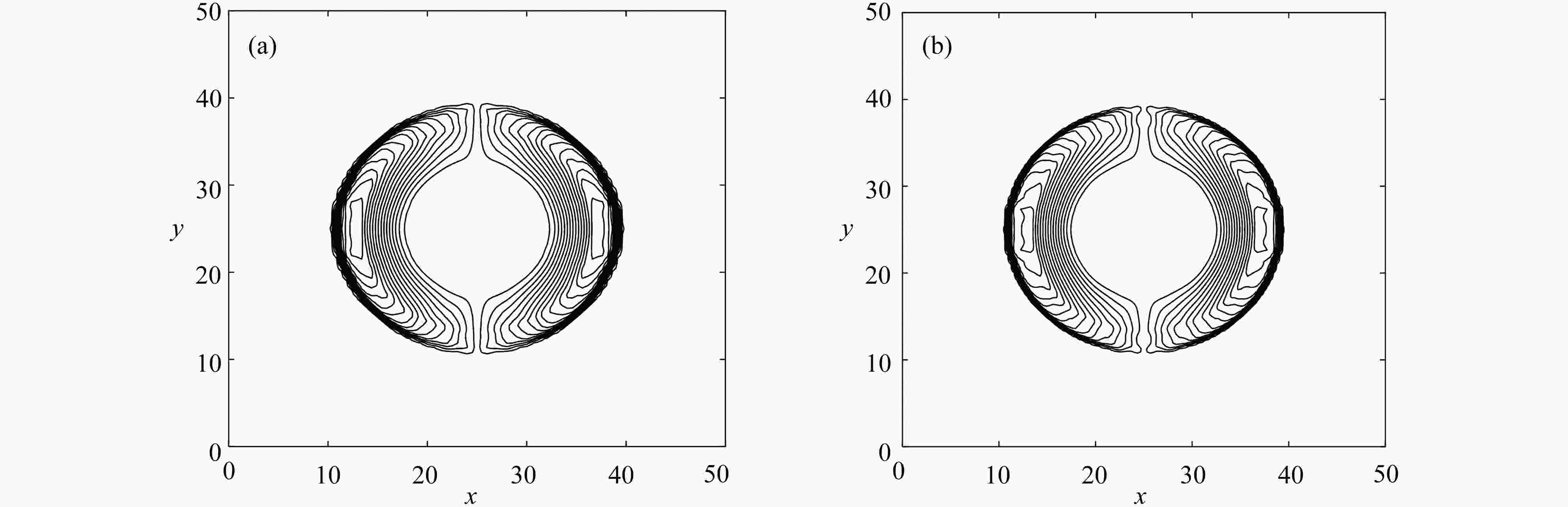
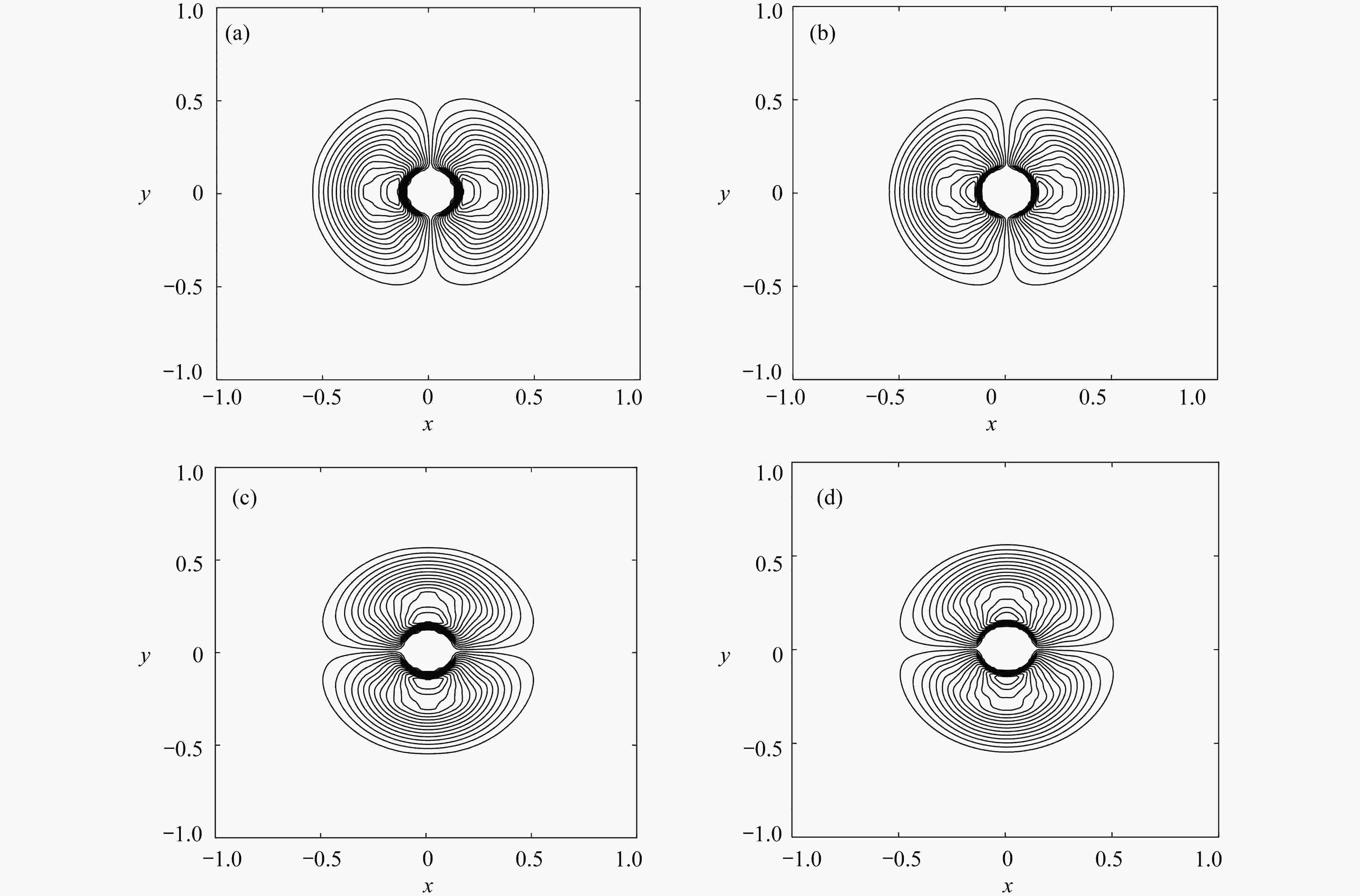
图 3 二维圆柱溃坝问题速度图：(a) 非混合格式x方向的速度u；(b) 混合格式x方向的速度u；(c) 非混合格式y方向的速度v；(d) 混合格式y方向的速度v
Figure 3. The velocity contour for the 2D cylindrical dam-break problem: (a) the non-mixed scheme x direction velocity u results; (b) the mixed scheme x direction velocity u results; (c) the non-mixed scheme y direction velocity v results; (d) the mixed scheme y direction velocity v results
图 5 二维圆形溃坝问题密度等值线图：(a) 非混合格式密度结果； (b) 混合格式密度结果
Figure 5. The density contour for the 2D circular dam-break problem: (a) the non-mixed scheme density results; (b) the mixed scheme density results
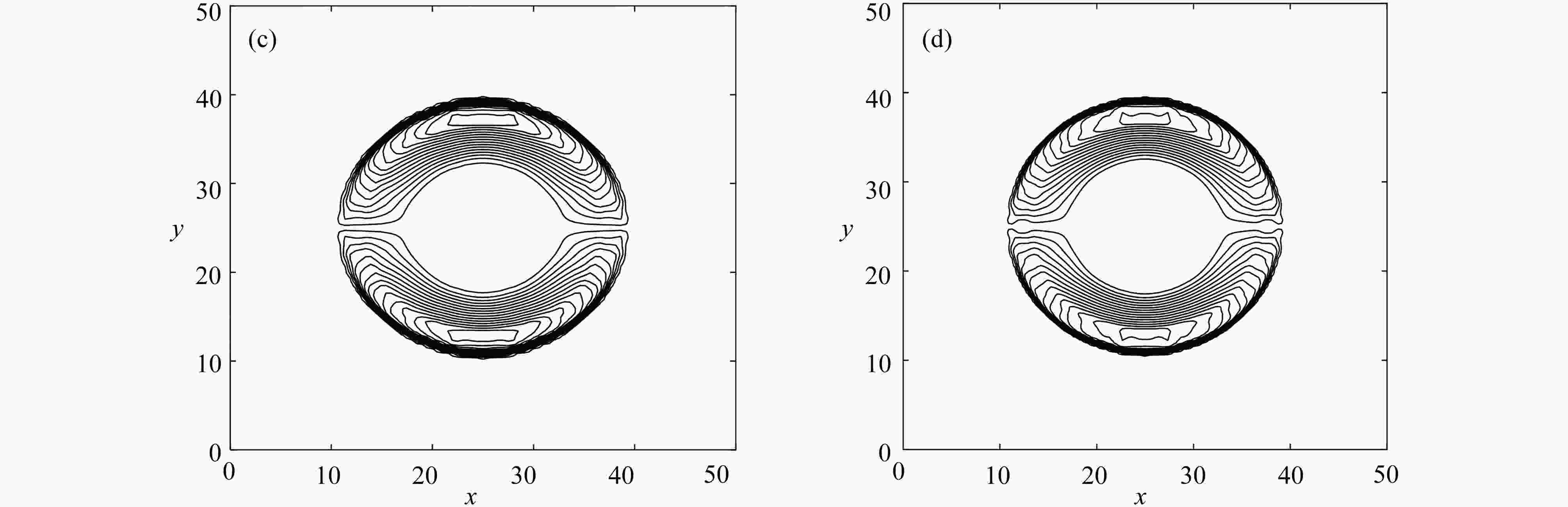
图 6 二维圆形溃坝问题速度图：(a) 非混合格式x方向的速度u；(b) 混合格式x方向的速度u；(c) 非混合格式y方向的速度v；(d) 混合格式y方向的速度v
Figure 6. The velocity contour for the 2D circular dam-break problem: (a) the non-mixed scheme x direction velocity u results; (b) the mixed scheme x direction velocity u results; (c) the non-mixed scheme y direction velocity v results; (d) the mixed scheme y direction velocity v results
图 8 二维激波聚焦问题密度等值线图：(a) 非混合格式密度结果； (b) 混合格式密度结果
Figure 8. The density contour for the 2D shock wave focusing problem: (a) the non-mixed scheme density results; (b) the mixed scheme density results
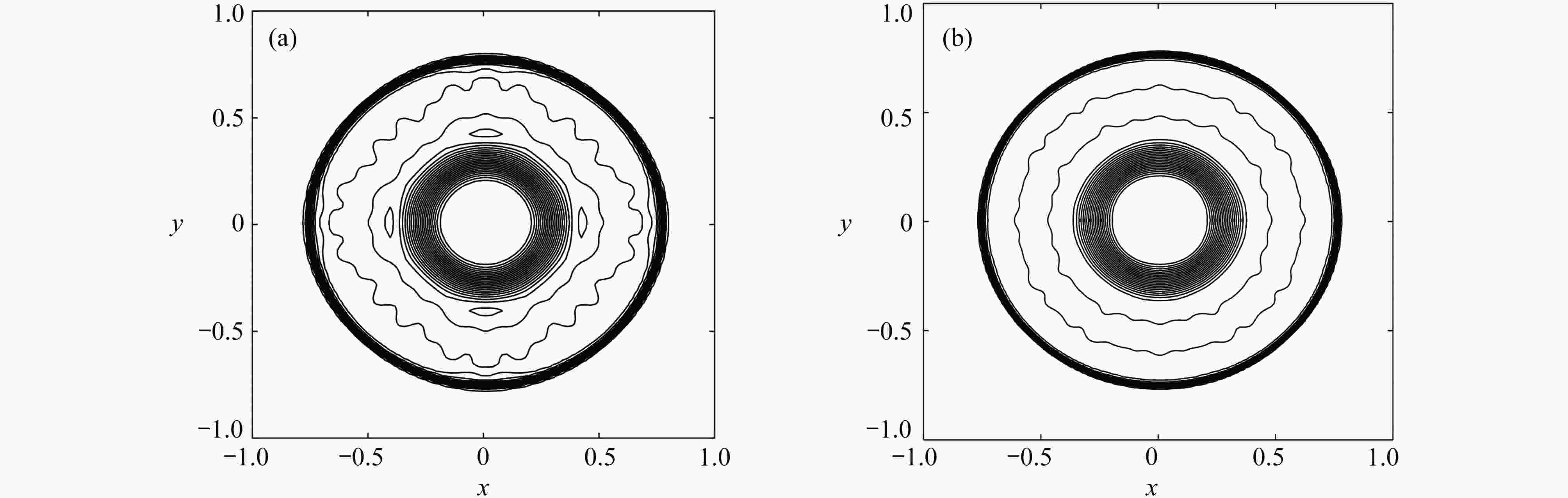
图 9 二维激波聚焦问题速度图：(a) 非混合格式x方向的速度u； (b) 混合格式x方向的速度u；(c) 非混合格式y方向的速度v ； (d) 混合格式y方向的速度v
Figure 9. The velocity contour for the 2D shock wave focusing problem: (a) the non-mixed scheme x direction velocity u results; (b) the mixed scheme x direction velocity u results; (c) the non-mixed scheme y direction velocity v results; (d) the mixed scheme y direction velocity v results
图 11 二维潮汐问题密度等值线图：(a) 非混合格式密度结果；(b) 混合格式密度结果
Figure 11. The density contour map for the 2D tidal problem: (a) the non-mixed scheme density results; (b) the mixed scheme density results
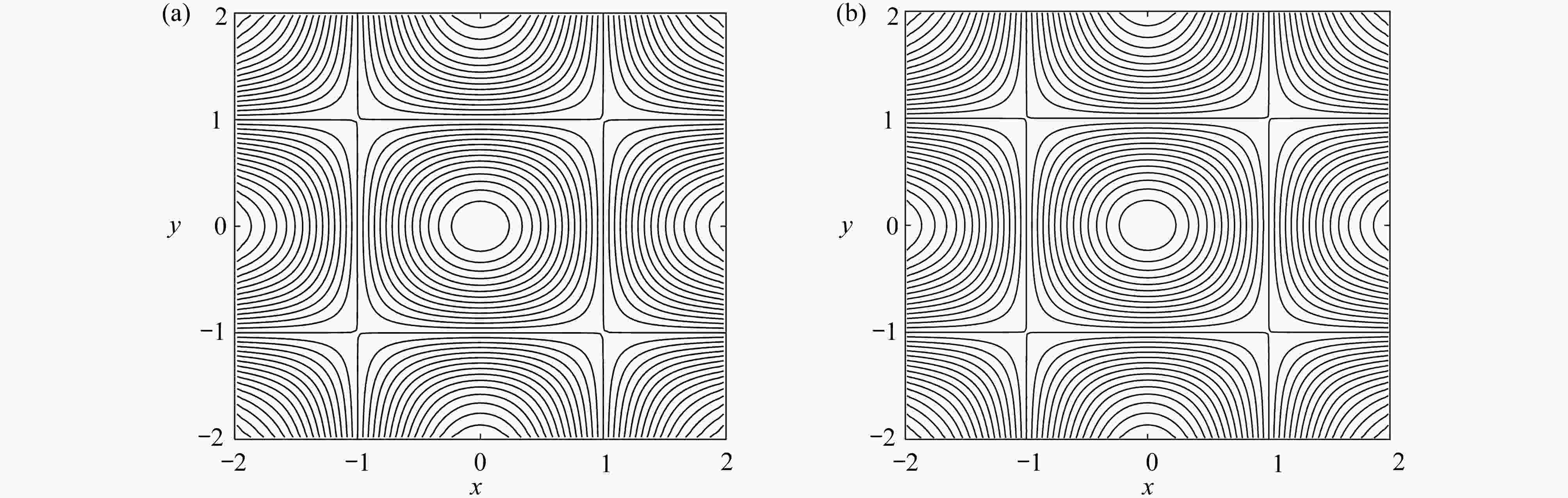
图 12 二维潮汐问题速度图：(a) 非混合格式x方向的速度u；(b) 混合格式x方向的速度u；(c) 非混合格式y方向的速度v；(d) 混合格式y方向的速度v
Figure 12. The velocity contour for the 2D tidal problem: (a) the non-mixed scheme x direction velocity u results; (b) the mixed scheme x direction velocity v results; (c) the non-mixed scheme y direction velocity v results; (d) the mixed scheme y=direction velocity v results
-
[1] TADMOR E. The numerical viscosity of entropy stable schemes for systems of conservation laws: Ⅰ[J]. Mathematics of Computation, 1987, 49(179): 91-103. doi: 10.1090/S0025-5718-1987-0890255-3 [2] ROE P L. Affordable, entropy-consistent Euler flux functions Ⅱ: entropy production at shocks[J]. Journal of Computational Physics, 2009, 228(15): 5410-5436. doi: 10.1016/j.jcp.2009.04.021 [3] 程晓晗, 聂玉峰, 蔡力. 基于WENO重构的熵稳定格式求解浅水方程[J]. 计算物理, 2015, 32(5): 523-528. (CHENG Xiaohan, NIE Yufeng, CAI Li. WENO based entropy stable scheme for shallow water equations[J]. Computational Physics, 2015, 32(5): 523-528.(in Chinese) doi: 10.3969/j.issn.1001-246X.2015.05.003 [4] LIU Q S, LIU Y Q, FENG J H. The scaled entropy variables reconstruction for entropy stable schemes with application to shallow water equations[J]. Computers & Fluids, 2019, 192(15): 1-15. [5] 王令, 郑素佩. 基于移动网格的熵稳定格式求解浅水波方程[J]. 水动力学研究与进展(A辑), 2020, 35(2): 80-88. (WANG Ling, ZHENG Supei. Solving shallow water wave equation based on moving grid entropy stable scheme[J]. Chinese Journal of Hydrodynamics, 2020, 35(2): 80-88.(in Chinese) [6] LEVY D W, POWELL K G, VAN LEER B. Use of a rotated Riemann solver for the two-dimensional Euler equations[J]. Journal of Computational Physics, 1993, 106(2): 201-214. doi: 10.1016/S0021-9991(83)71103-4 [7] REN Y X. A robust shock-capturing scheme based on rotated Riemann solvers[J]. Computer & Fluids, 2003, 32(10): 1379-1403. [8] ZHANG F, LIU J. Evaluation of rotated upwind schemes for contact discontinuity and strong shock[J]. Computer & Fluids, 2016, 134(4): 11-22. [9] 郑素佩, 王令, 王苗苗. 求解二维浅水波方程的移动网格旋转通量法[J]. 应用数学和力学, 2020, 41(1): 42-53. (ZHENG Supei, WANG Ling, WANG Miaomiao. Solution of 2D shallow water wave equation with the moving-grid rotating-invariance method[J]. Applied Mathematics and Mechanics, 2020, 41(1): 42-53.(in Chinese) [10] NISHIKAWA H, KITAMURA K. Very simple, carbuncle-free, boundary-layer-resolving, rotated-hybrid Riemann solvers[J]. Journal of Computational Physics, 2008, 227(4): 2560-2581. doi: 10.1016/j.jcp.2007.11.003 [11] 刘友琼, 封建湖, 任炯, 等. 求解多维Euler方程的二阶旋转混合型格式[J]. 应用数学和力学, 2014, 35(5): 542-553. (LIU Youqiong, FENG Jianhu, REN Jiong, et al. Second order rotational hybrid scheme for solving multi-dimensional Euler equation[J]. Applied Mathematics and Mechanics, 2014, 35(5): 542-553.(in Chinese) doi: 10.3879/j.issn.1000-0887.2014.05.008 [12] 贾豆, 郑素佩. 求解二维Euler方程的旋转通量混合格式[J]. 应用数学和力学, 2021, 42(2): 170-179. (JIA Dou, ZHENG Supei. A hybrid scheme of rotational flux for solving 2D Euler equations[J]. Applied Mathematics and Mechanics, 2021, 42(2): 170-179.(in Chinese) [13] THANH M D, KARIM M F, ISMAIL A I M. Well-balanced scheme for shallow water equations with arbitrary topography[J]. International Journal of Dynamical Systems & Different Equations, 2008, 1(3): 196-204. [14] TORO F. Riemann Solvers and Numerical Methods for Fluid Dynamics[M]. Berlin: Springer, 2013. [15] CHENG X H. A fourth order entropy stable scheme for hyperbolic conservation laws[J]. Entropy, 2019, 21(5): 508-527. doi: 10.3390/e21050508 [16] BÜRGER R, MÉNDEZ P E, PARÉS C. On entropy stable schemes for degenerate parabolic multispecies kinematic flow models[J]. Numerical Methods for Partial Differential Equation, 2019, 35(5): 1847-1872. doi: 10.1002/num.22381 [17] RITESH K D, BISWARUP B. Suitable diffusion for constructing non-oscillatory entropy stable schemes[J]. Journal of Computational Physics, 2018, 372(5): 912-930. [18] BISWARUP B, RITESH K D. Low dissipative entropy stable schemes using third order WENO and TVD reconstructions[J]. Advances in Computational Mathematics, 2018, 44(4): 1153-1181. doi: 10.1007/s10444-017-9576-2 [19] RAY D, CHANDRASHEKAR P, FJORDHOLM U S. Entropy stable scheme on two-dimensional unstructured grids for Euler equations[J]. Communications in Computational Physics, 2016, 19(5): 1111-1140. doi: 10.4208/cicp.scpde14.43s [20] HARTEN A, LAX P D, VAN LEER B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws[J]. SIAM Review, 1983, 25(1): 35-61. doi: 10.1137/1025002 [21] PREBEG M, FLÅTTEN T, MÜLLER B. Large time step HLL and HLLC schemes[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 2018, 52(4): 1239-1260. doi: 10.1051/m2an/2017051 [22] SANGEETH S, MANDAL J C. A cure for numerical shock instability in HLLC Riemann solver using antidiffusion control[J]. Computers & Fluids, 2018, 174(3): 144-166. [23] GOETZ C R, BALSARA D S, DUMBSER M. A family of HLL-type solvers for the generalized Riemann problem[J]. Computers & Fluids, 2018, 169(70): 201-212. [24] GOTTLIEB S, KETCHESON D I, SHU C W. High order strong stability preserving time discretizations[J]. Journal of Scientific Computing, 2009, 38(3): 251-289. -
下载:
点击查看大图
计量
- 文章访问数: 501
- HTML全文浏览量: 225
- PDF下载量: 84
- 被引次数: 0
