Optimal Leader-Following Consensus Control of Fractional-Order Multi-Agent Systems Based on the Actor-Critic Algorithm
-
摘要:
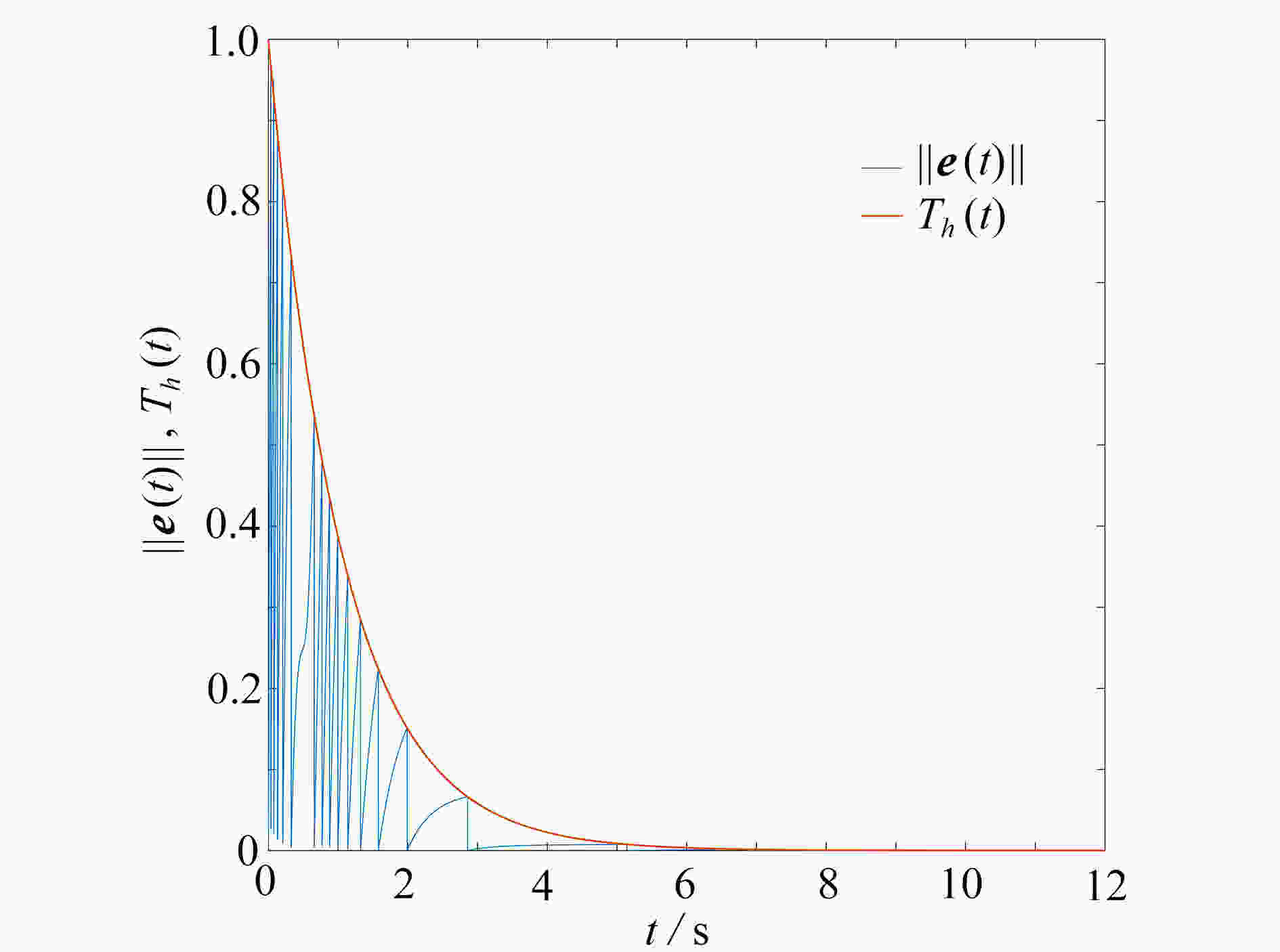
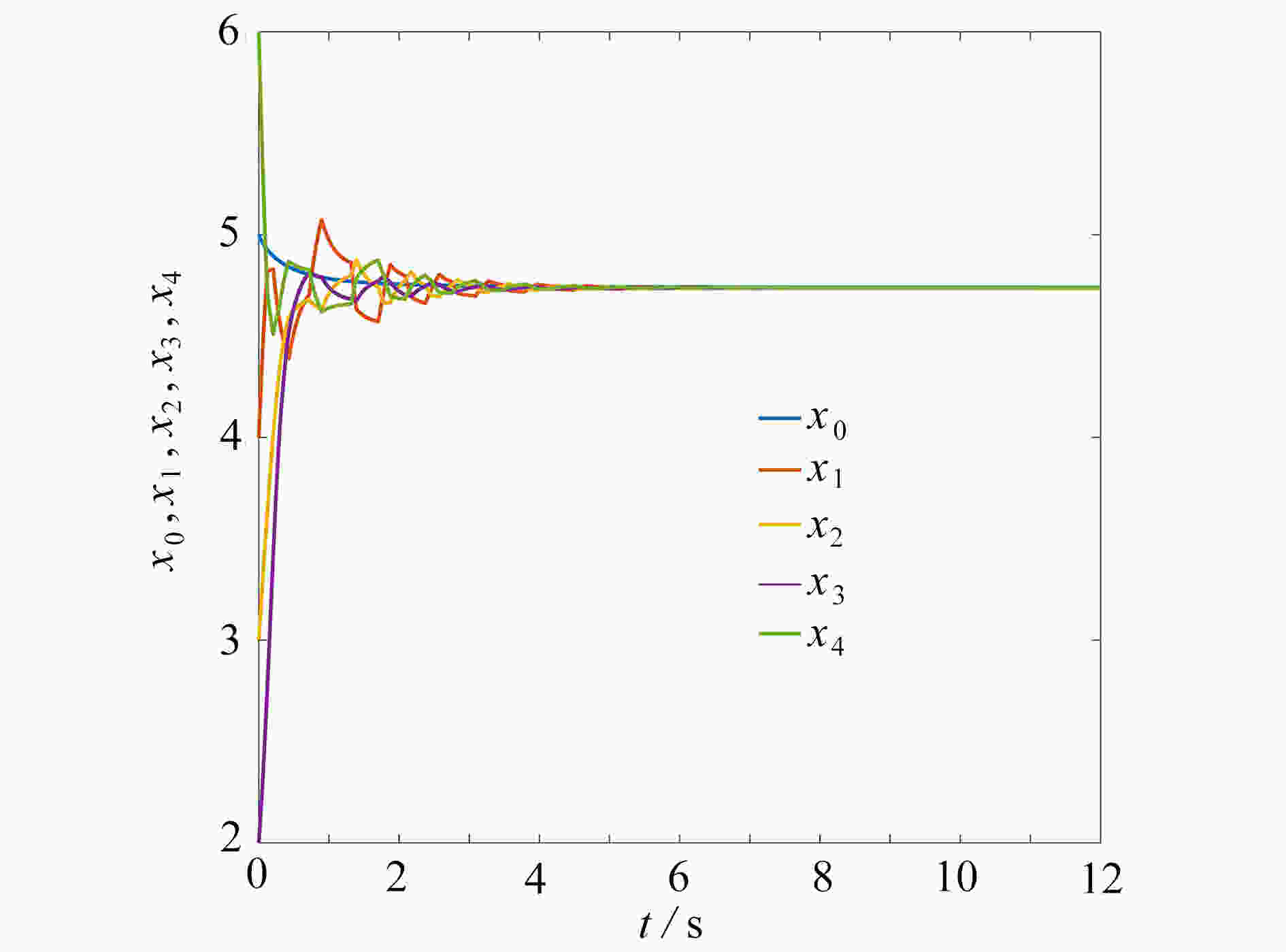
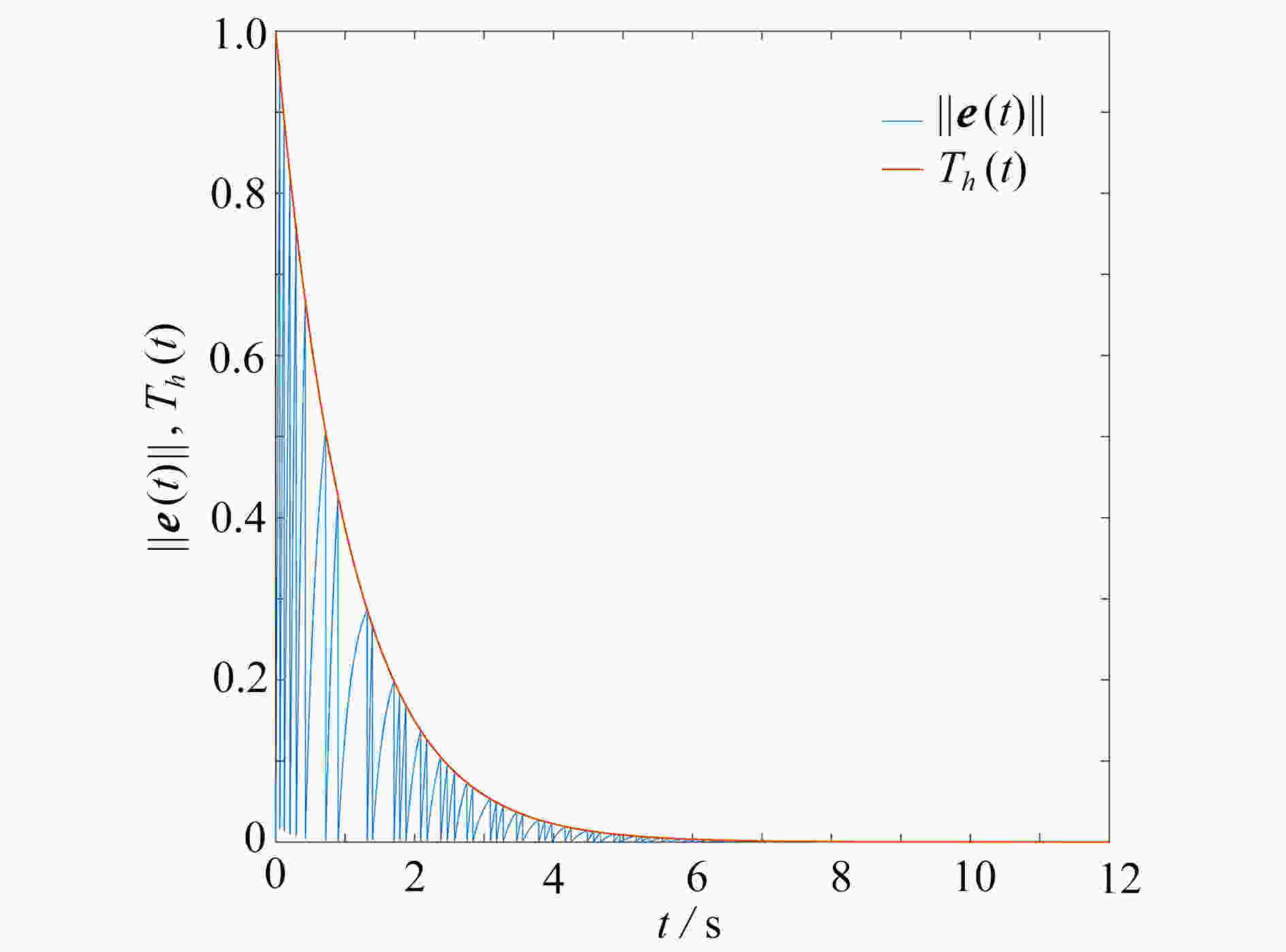
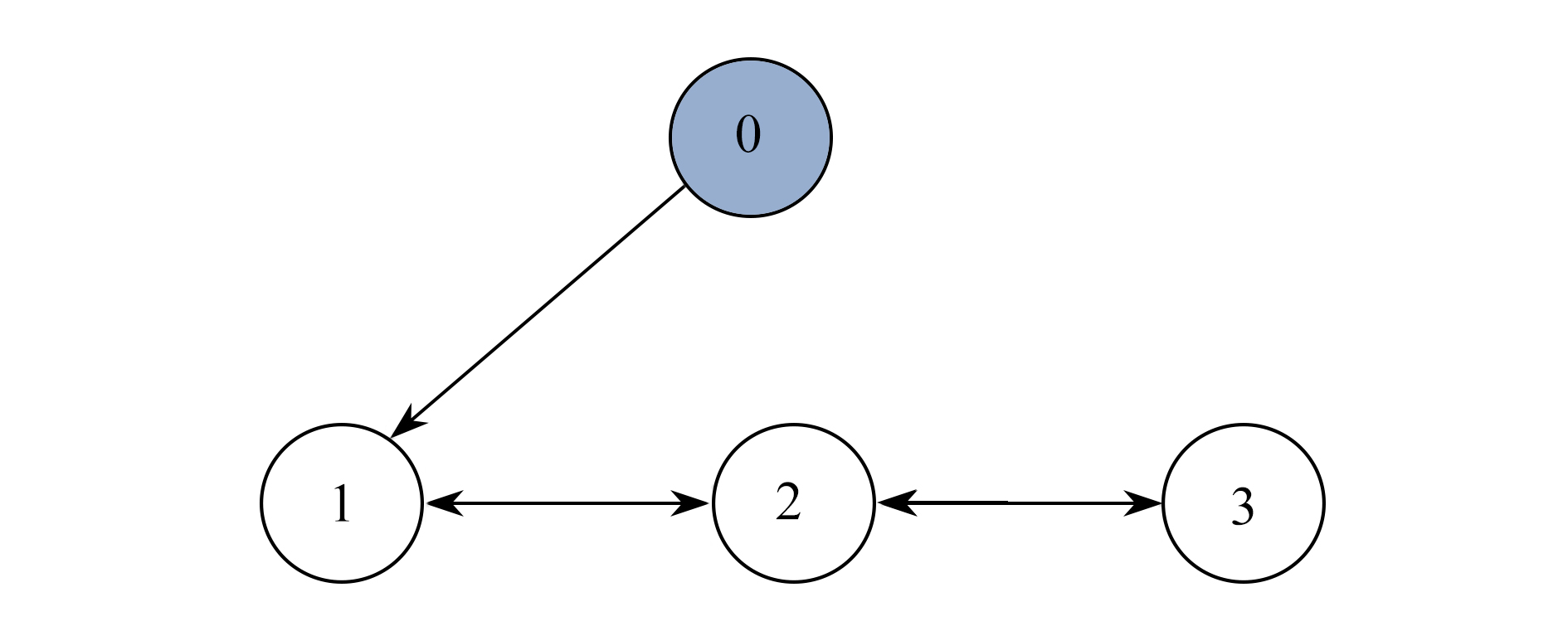
研究了分数阶多自主体系统的最优主-从一致性问题。在考虑控制器周期间歇的前提下，将分数阶微分的一阶近似逼近式、事件触发机制和强化学习中的actor-critic算法有机整合，设计了基于周期间歇事件触发策略的强化学习算法结构。最后，通过数值仿真实验证明了该算法的可行性和有效性。
-
关键词:
- 分数阶多自主体系统 /
- actor-critic算法 /
- 最优主-从一致性 /
- 事件触发 /
- 间歇
Abstract:Aimed at the optimal leader-following consensus problem of fractional-order multi-agent systems, an reinforcement learning strategy was designed based on the intermittent event trigger. With the periodic intermittent strategy as the basic mechanism, the event trigger and the actor-critic algorithm in reinforcement learning were organically integrated. According to the 1st-order approximation of the fractional differential, the reinforcement learning algorithm structure based on the periodic intermittent event trigger strategy was proposed. Finally, the feasibility and effectiveness of the algorithm was proved through numerical simulation experiments.
-
图 1 多自主体系统网络拓扑图(1个领导者，3个追随者)
Figure 1. The net topology of the multi-agent system (1 leader, 3 followers)
图 2 无控制器作用时，各自主体的状态轨迹(1个领导者，3个追随者)
Figure 2. State trajectories of each agent without controllers (1 leader, 3 followers)
图 3 各自主体的状态轨迹(1个领导者，3个追随者)
Figure 3. State trajectories of each agent (1 leader, 3 followers)
图 4
$\|\boldsymbol{e}\left(t\right)\| $ 及触发阈值变化曲线(1个领导者，3个追随者)Figure 4. The error and the trigger threshold (1 leader, 3 followers)
图 5 周期间歇事件触发时刻分布
Figure 5. The event-trigger moment distribution of periodic intermittence
图 6 多自主体系统网络拓扑图(1个领导者，4个追随者)
Figure 6. The net topology of the multi-agent system (1 leader, 4 followers)
图 7 无控制器作用时，各自主体的状态轨迹(1个领导者，4个追随者)
Figure 7. State trajectories of each agent without controllers (1 leader, 4 followers)
图 8 各自主体的状态轨迹(1个领导者，4个追随者)
Figure 8. State trajectories of each agent (1 leader, 4 followers)
图 9
$\left|\left|{{\boldsymbol{e}}}\left(t\right)\right|\right|$ 及触发阈值变化曲线(1个领导者，4个追随者)Figure 9. The error and the trigger threshold (1 leader, 4 followers)
图 12
$\left|\left|{{\boldsymbol{e}}}\left(t\right)\right|\right|$ 及触发阈值变化曲线Figure 12. The error
$\left|\left|{{\boldsymbol{e}}}\left(t\right)\right|\right|$ and the trigger threshold表 1 网络参数设置
Table 1. Values of networks’ parameters
parameter meaning value ${\beta }_{{\rm{c}}1}$ learning rate of the critic network 0.1 ${\beta }_{{\rm{a}}1}$ learning rate of the actor network 0.1 ${T}_{{\rm{c}},\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r} }$ threshold for the critic network $ {10^{ - 10}} $ ${T}_{{\rm{a}},\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r} }$ threshold for the actor network $ {10^{ - 10}} $ ${N}_{{\rm{c}}1}$ number of hidden nodes in the critic network 5 ${N}_{{\rm{a}}1}$ number of hidden nodes in the critic network 3 ${\psi }_{{\rm{c}}}\left(\cdot \right)$ activation function of the critic network $ \mathrm{tan}\mathrm{h}\left(\cdot \right) $ ${\psi }_{{\rm{a}}}\left(\cdot \right)$ activation function of the actor network $ \mathrm{tan}\mathrm{h}\left(\cdot \right) $ 
下载: 导出CSV
-
[1] CORTÉS J, BULLO F. Coordination and geometric optimization via distributed dynamical systems[J]. SIAM Journal on Control and Optimization, 2005, 44(5): 1543-1574. doi: 10.1137/S0363012903428652 [2] FAX J A, MURRAY R M. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476. doi: 10.1109/TAC.2004.834433 [3] YU W W, CHEN G R, WANG Z D, et al. Distributed consensus filtering in sensor networks[J]. IEEE Transactions on Systems, Man, and Cybernetics (Part B) : Cybernetics, 2009, 39(6): 1568-1577. doi: 10.1109/TSMCB.2009.2021254 [4] BEARD R W, MCLAIN T W, GOODRICH M A, et al. Coordinated target assignment and intercept for unmanned air vehicles[J]. IEEE Transactions on Robotics and Automation, 2002, 18(6): 911-922. doi: 10.1109/TRA.2002.805653 [5] FAX J A, MURRAY R M. Information flow and cooperative control of vehicle formations[J]. IFAC Proceedings Volumes, 2002, 35(1): 115-120. [6] YU W W, WANG H, CHENG F, et al. Second-order consensus in multiagent systems via distributed sliding mode control[J]. IEEE Transactions on Cybernetics, 2017, 47(8): 1872-1881. doi: 10.1109/TCYB.2016.2623901 [7] YU W W, CHEN G R, CAO M, et al. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics[J]. IEEE Transactions on Systems, Man, and Cybernetics (Part B) : Cybernetics, 2010, 40(3): 881-891. doi: 10.1109/TSMCB.2009.2031624 [8] WEN G H, YU W W, XIA Y Q, et al. Distributed tracking of nonlinear multiagent systems under directed switching topology: an observer-based protocol[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 47(5): 869-881. doi: 10.1109/TSMC.2016.2564929 [9] WEN G H, YU W W, LI Z H, et al. Neuro-adaptive consensus tracking of multiagent systems with a high-dimensional leader[J]. IEEE Transactions on Cybernetics, 2017, 47(7): 1730-1742. doi: 10.1109/TCYB.2016.2556002 [10] SUN W, LI Y, LI C P, et al. Convergence speed of a fractional order consensus algorithm over undirected scale-free networks[J]. Asian Journal of Control, 2011, 13(6): 936-946. doi: 10.1002/asjc.390 [11] CHAO S, CAO J D. Consensus of fractional-order linear systems[C]//2013 9th Asian Control Conference (ASCC). Istanbul, Turkey, 2013. [12] YU W W, LI Y, WEN G H, et al. Observer design for tracking consensus in second-order multi-agent systems: fractional order less than two[J]. IEEE Transactions on Automatic Control, 2017, 62(2): 894-900. doi: 10.1109/TAC.2016.2560145 [13] ASTROM K J, BERNHARDSSON B. Comparison of periodic and event based sampling for first-order stochastic systems[C]//14th IFAC World Congress. Beijing, China, 1999. [14] DIMAROGONAS D V, JOHANSSON K H. Event-triggered control for multi-agent systems[C]//Proceedings of the 48th IEEE Conference on Decision and Control, CDC 2009, Combined With the 28th Chinese Control Conference. Shanghai, China, 2009. [15] XU G H, CHI M, HE D X, et al. Fractional-order consensus of multi-agent systems with event-triggered control[C]//2014 11th IEEE International Conference on Control & Automation (ICCA). Taichung, 2014. [16] WANG F, YANG Y Q. Leader-following consensus of nonlinear fractional-order multi-agent systems via event-triggered control[J]. International Journal of Systems Science, 2017, 48(3): 571-577. [17] YE Y Y, SU H S. Consensus of delayed fractional-order multiagent systems with intermittent sampled data[J]. IEEE Transactions on Industrial Informatics, 2019, 16(6): 3828-3837. [18] XU L G, LIU W, HU H X, et al. Exponential ultimate boundedness of fractional-order differential systems via periodically intermittent control[J]. Nonlinear Dynamics, 2019, 96(2): 1665-1675. doi: 10.1007/s11071-019-04877-y [19] XU Y, LI Q, LI W X. Periodically intermittent discrete observation control for synchronization of fractional-order coupled systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 74: 219-235. doi: 10.1016/j.cnsns.2019.03.014 [20] CHANG Q, HU A H, YANG Y Q, et al. Pinning exponential boundedness of fractional-order multi-agent systems with intermittent combination event-triggered protocol[J]. International Journal of Systems Science, 2020, 52(4): 874-888. [21] HU A, HP JU, HU M. Consensus of nonlinear multiagent systems with intermittent dynamic event-triggered protocols[J]. Nonlinear Dynamics, 2021, 104: 1299-1313. doi: 10.1007/s11071-021-06321-6 [22] LIU X Y, FU H B, LIU L. Leader-following mean square consensus of stochastic multi-agent systems via periodically intermittent event-triggered control[J]. Neural Processing Letters, 2020, 53(1): 275-298. [23] REN W, BEARD R W, ATKINS E M. A survey of consensus problems in multi-agent coordination[C]//Proceedings of the 2005, American Control Conference. Portland, OR, USA, 2005. [24] ZHANG H G, JIANG H, LUO Y H, et al. Data-driven optimal consensus control for discrete-time multi-agent systems with unknown dynamics using reinforcement learning method[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4091-4100. doi: 10.1109/TIE.2016.2542134 [25] ZHAO W, YU W W, ZHANG H P. Event-triggered optimal consensus tracking control for multi-agent systems with unknown internal states and disturbances[J]. Nonlinear Analysis Hybrid Systems, 2019, 33: 227-248. doi: 10.1016/j.nahs.2019.03.003 [26] DONG L, ZHONG X N, SUN C Y, et al. Event-triggered adaptive dynamic programming for continuous-time systems with control constraints[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 28(8): 1941-1952. [27] 刘晨, 刘磊. 基于事件触发策略的多智能体系统的最优主-从一致性分析[J]. 应用数学和力学, 2019, 40(11): 1278-1288. (LIU Chen, LIU Lei. Optimal leader-follower consensus of multi-agent systems based on the event-triggered strategy[J]. Applied Mathematics and Mechanics, 2019, 40(11): 1278-1288.(in Chinese) [28] PODLUBNY I. Fractional Differential Equations[M]. New York, USA: Academic, 1999. [29] ATANACKOVIC T M, STANKOVIC B. On a numerical scheme for solving differential equations of fractional order[J]. Mechanics Research Communications, 2008, 35(7): 429-438. [30] POOSEH S, ALMEIDA R, TORRES D. Fractional order optimal control problems with free terminal time[J]. Journal of Industrial & Management Optimization, 2014, 10(2): 363-381. [31] ILBAS A A A, SRIVASTAVA H M, TRUJILLO J J. Theory and Applications of Fractional Differential Equations[M]. North-Holland Mathematics Studies, 204. Elsevier, 2006. -
计量
- 文章访问数: 1156
- HTML全文浏览量: 525
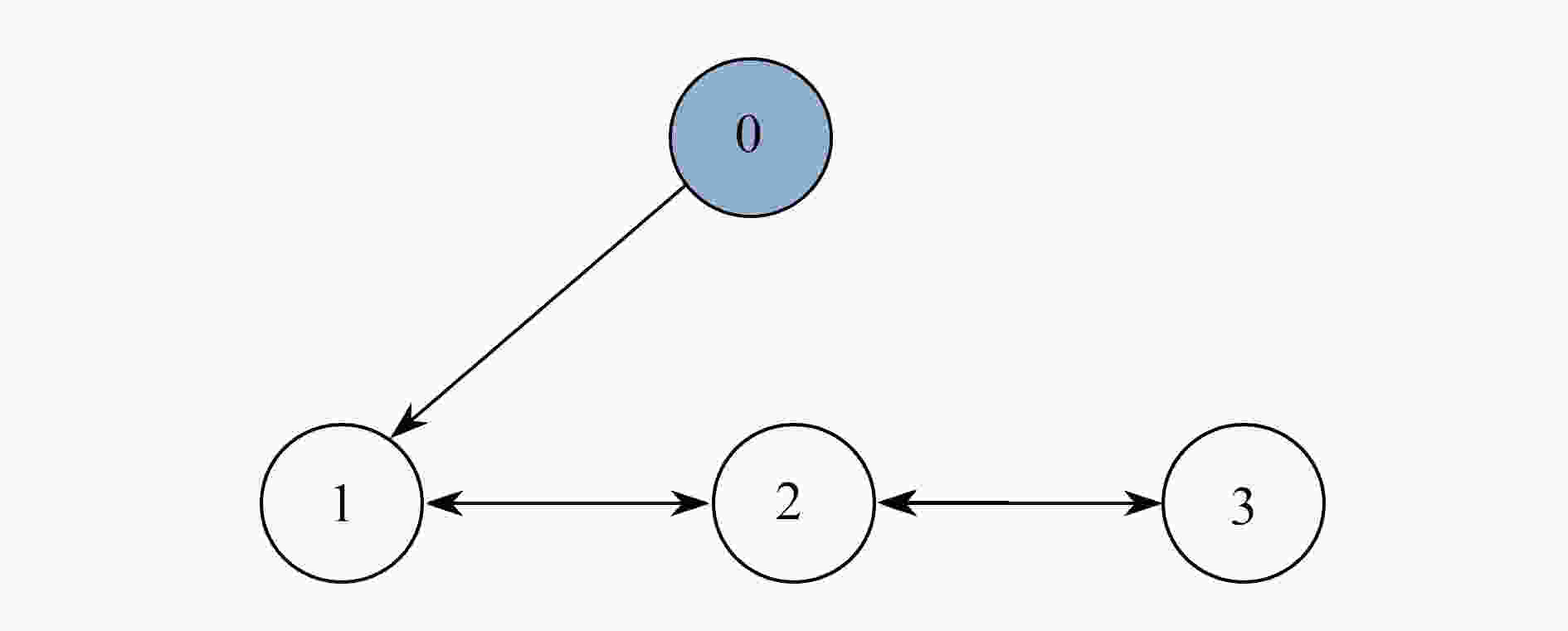
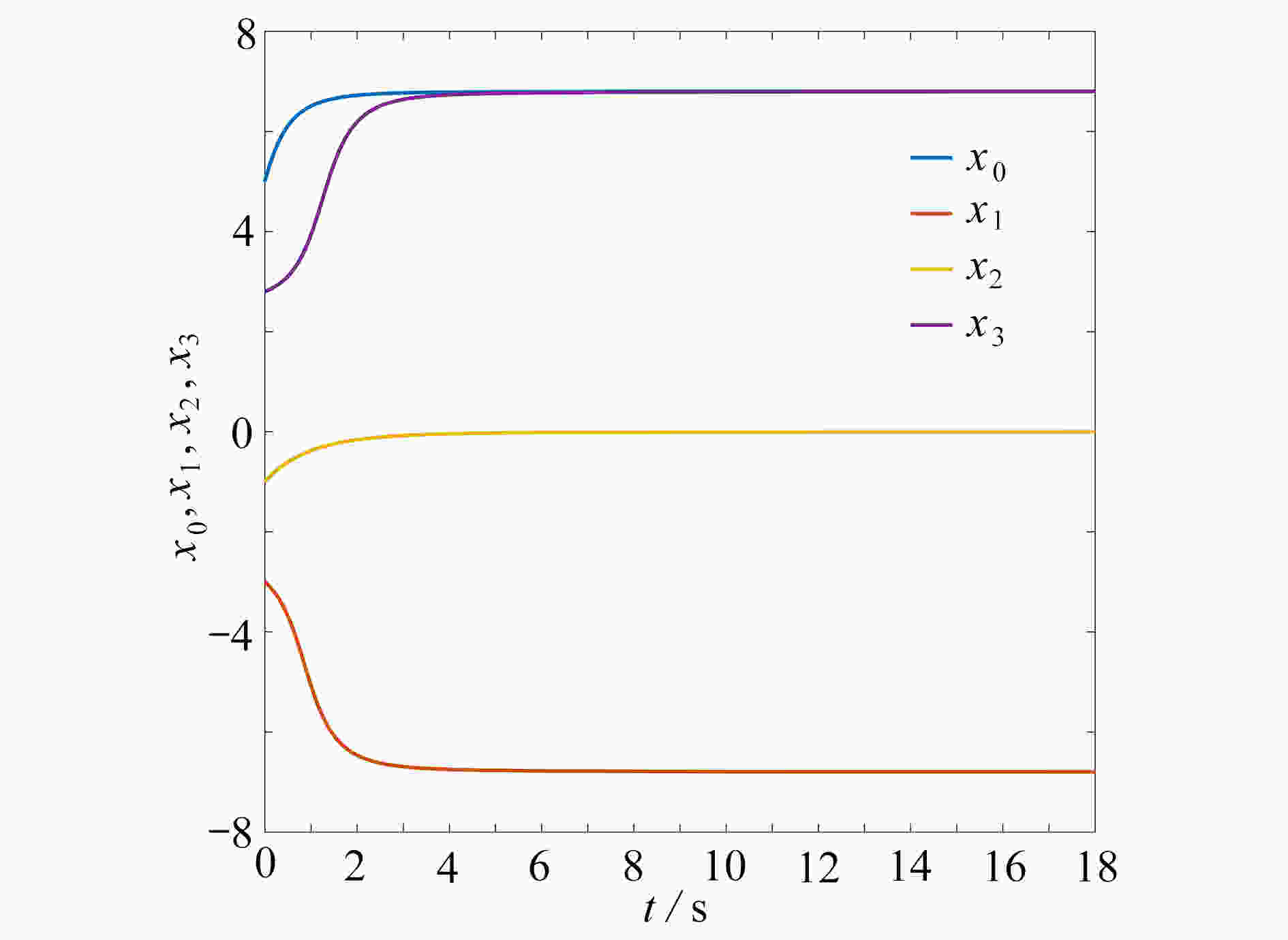
- PDF下载量: 67
- 被引次数: 0
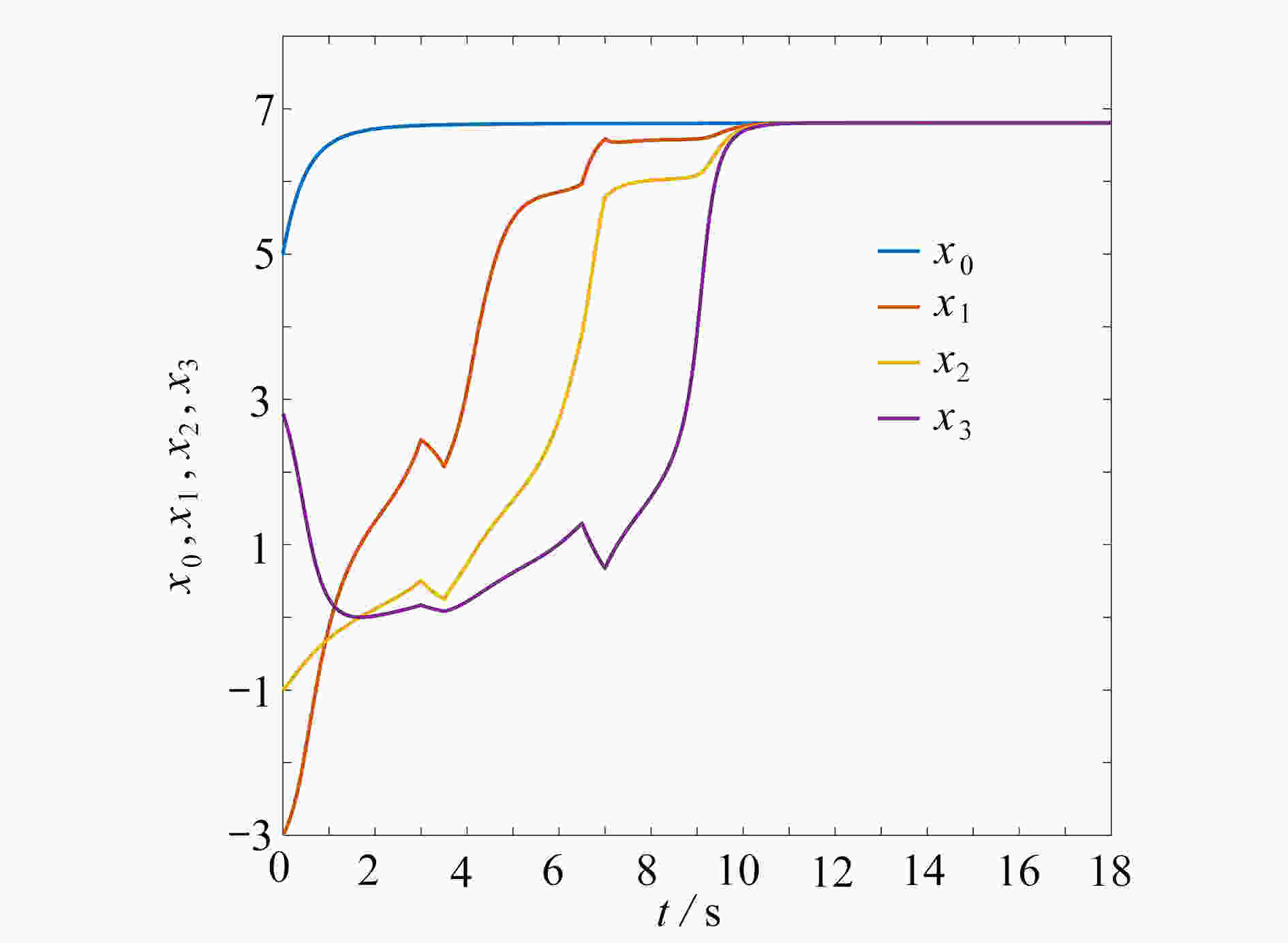
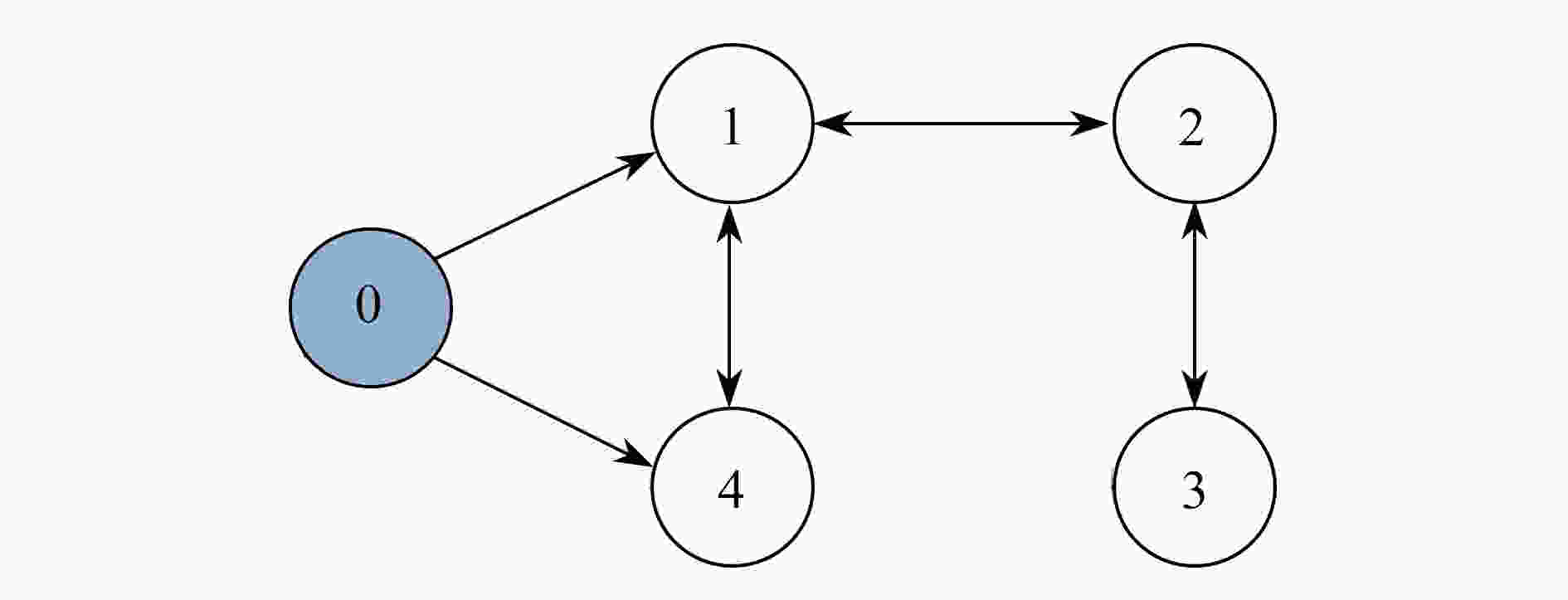
渝公网安备50010802005915号