Variational Regularization of the Inverse Problem of a Class of Nonlinear Time-Fractional Diffusion Equations
-
摘要:
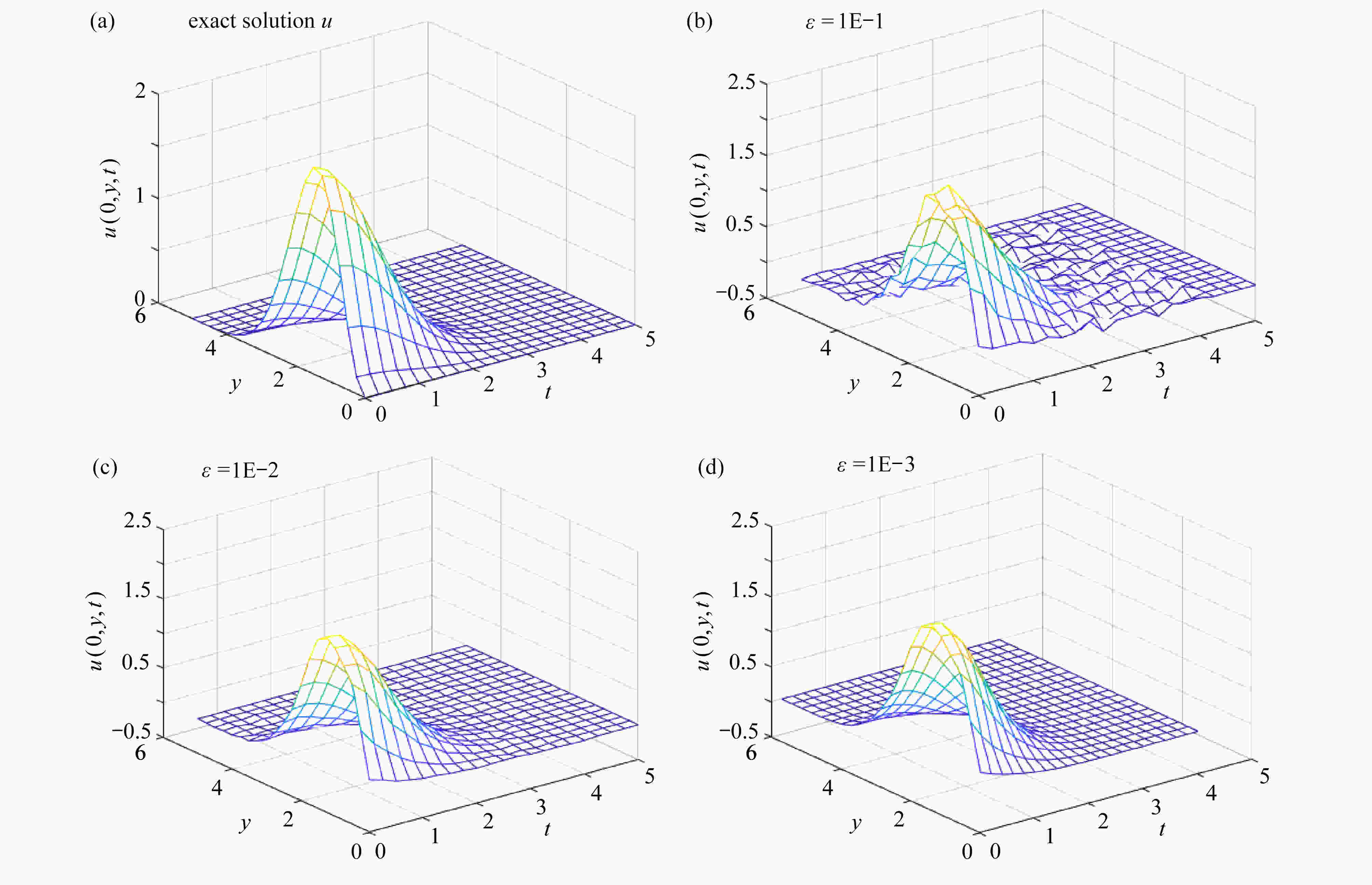
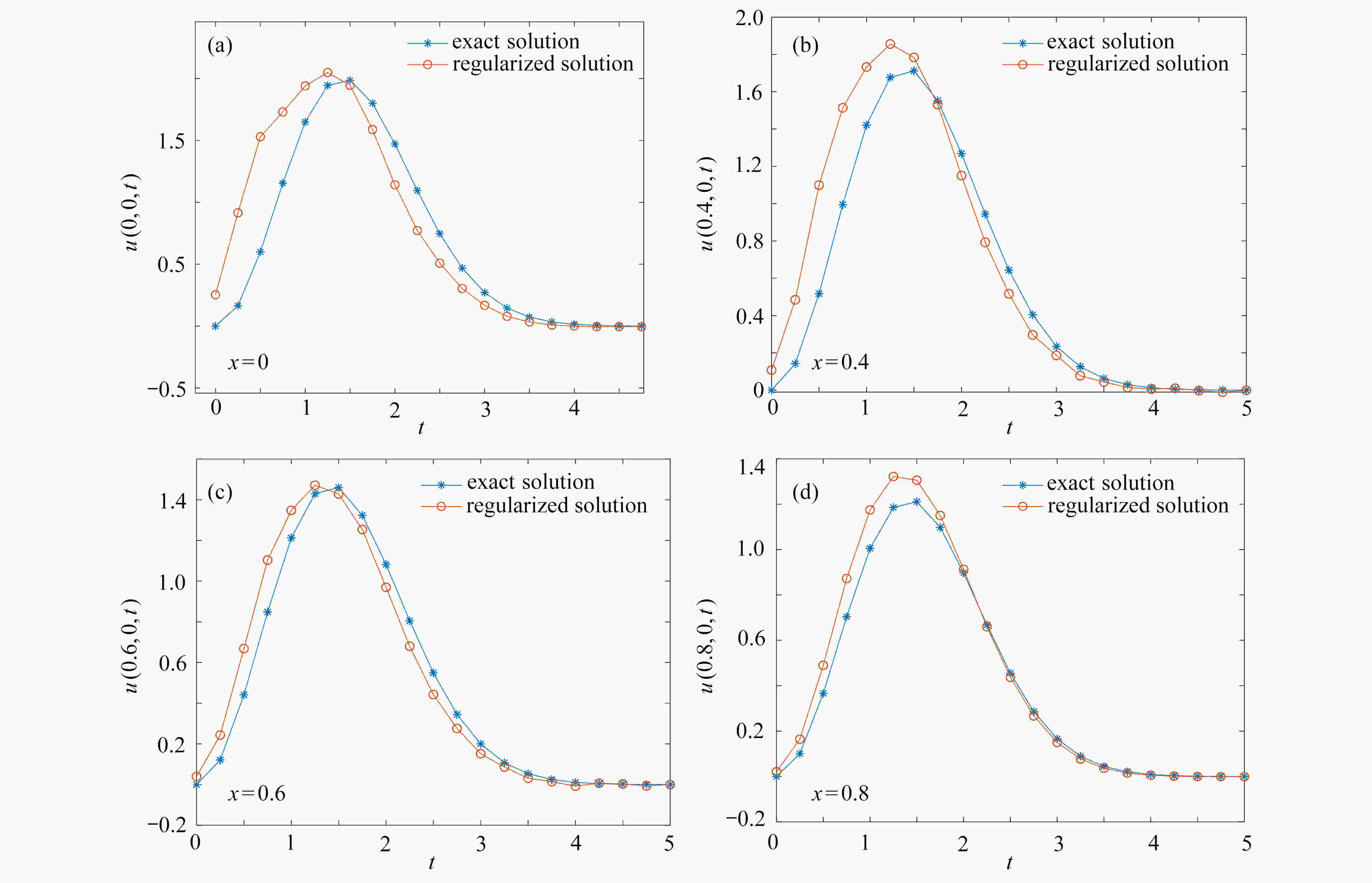
考虑了一类二维非线性时间分数阶扩散方程，并从最终位置获取的测量数据来反演物质在u(0, y, t)处的物理信息。这个问题是严重不适定的，即问题的解并不连续依赖于测量数据，因此提出了变分型正则化方法来稳定求解该问题。给出了精确解与正则近似解之间的误差估计，数值算例验证了该方法的有效性。
Abstract:The nonlinear time-fractional diffusion equations were considered in the 2D domain, and the physical information in initial state
\begin{document}$ u(0,y,t) $\end{document} of the material was recovered from the measured data in the final state. This problem is seriously ill-posed, that is, the solution to this problem does not continuously depend on the measured data. Therefore, a variational regularization method was proposed to construct the approximate solution to the problem, and the convergence error estimates of the exact and approximate solutions were obtained under the assumption of the priori bounds on the exact solutions. Finally, a numerical example was given to verify the effectiveness of the proposed method.
-
图 1 在
$ {x}=0 $ 时的精确解和不同误差水平下的正则近似解$ {{u}}^{{\alpha },{\varepsilon }} $ Figure 1. Exact solution
$ u $ at$ x=0 $ and regularized approximate solution$ {u}^{\alpha ,\varepsilon } $ curves corresponding to different error levels
图 2 正则化解和精确解在不同x取值下的比较(y=0)
Figure 2. The exact solution and its regularized solution curves corresponding to different x values
( y =0) 表 1 不同误差水平下的相对误差
$ {E}_{{\rm{r}}} $ Table 1. Relative errors corresponding to different error levels
$ {x} $ $ {{E}}_{\rm{r}} $ $ {\varepsilon }=1{\rm{E}}-1 $ $ {\varepsilon }=1{\rm{E}}-2 $ $ {\varepsilon }=1{\rm{E}}-3 $ 0 2.749E−1 2.685E−1 2.682E−1 0.1 2.639E−1 2.522E−1 2.520E−1 0.2 2.409E−1 2.367E−1 2.348E−1 0.3 2.251E−1 2.219E−1 2.227E−1 0.4 2.047E−1 2.017E−1 2.026E−1 0.5 1.848E−1 1.709E−1 1.713E−1 0.6 1.551E−1 1.366E−1 1.345E−1 0.7 1.213E−1 1.030E−1 1.026E−1 0.8 1.003E−1 8.010E−2 7.600E−2 0.9 9.800E−2 9.750E−2 9.470E−2 
下载: 导出CSV
-
[1] TARASOV V E, ZASLAVSKY G M. Fractional Ginzburg-Landau equation for fractal media[J]. Physica A: Statistical Mechanics & Its Applications, 2005, 354(15): 249-261. [2] METZLER R, KLAFTER J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach[J]. Physics Reports, 2000, 339(1): 1-77. doi: 10.1016/S0370-1573(00)00070-3 [3] MENDES R V. A fractional calculus interpretation of the fractional volatility model[J]. Nonlinear Dynamics, 2009, 55(4): 395-399. doi: 10.1007/s11071-008-9372-0 [4] GARRAPPA R, MORET I, POPOLIZIO M. Solving the time-fractional Schrödinger equation by Krylov projection methods[J]. Journal of Computational Physics, 2015, 293: 115-134. doi: 10.1016/j.jcp.2014.09.023 [5] 余钊圣, 林建忠. 粘弹性二阶流体混合层流场拟序结构的数值研究[J]. 应用数学和力学, 1998, 19(8): 671-677. (YU Zhaosheng, LIN Jianzhong. Numerical research on the coherent structure in the viscoelastic second-order mixing layers[J]. Applied Mathematics and Mechanics, 1998, 19(8): 671-677.(in Chinese) [6] JIANG Y J, MA J T. High-order finite element methods for time-fractional partial differential equations[J]. Journal of Computational and Applied Mathematics, 2011, 235(11): 3285-3290. doi: 10.1016/j.cam.2011.01.011 [7] ZHUANG P H, LIU F W. Implicit difference approximation for the two-dimensional space-time fractional diffusion equation[J]. Journal of Applied Mathematics & Informatics, 2007, 25(1): 269-282. [8] GAO G H, SUN H W, SUN Z Z. Stability and convergence of finite difference schemes for a class of time-fractional sub-diffusion equations based on certain superconvergence[J]. Journal of Computational Physics, 2015, 280: 510-528. doi: 10.1016/j.jcp.2014.09.033 [9] LUCHKO Y. Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation[J]. Computers and Mathematics With Applications, 2009, 59(5): 1766-1772. [10] MURIO D A. Stable numerical solution of a fractional-diffusion inverse heat conduction problem[J]. Computers & Mathematics With Applications, 2007, 53(10): 1492-1501. [11] CHENG H, FU C L. An iteration regularization for a time-fractional inverse diffusion problem[J]. Applied Mathematical Modelling, 2012, 36(11): 5642-5649. doi: 10.1016/j.apm.2012.01.016 [12] LIU S S, FENG L X. A modified kernel method for a time-fractional inverse diffusion problem[J]. Advances in Difference Equations, 2015, 342: 1-11. [13] LIU S S, FENG L X. A posteriori regularization parameter choice rule for a modified kernel method for a time-fractional inverse diffusion problem[J]. Journal of Computational and Applied Mathematics, 2019, 353: 355-366. doi: 10.1016/j.cam.2018.12.038 [14] ZHENG G H, WEI T. Spectral regularization method for solving a time-fractional inverse diffusion problem[J]. Applied Mathematics & Computation, 2011, 218(2): 396-405. [15] TUAN N H, KIRANE M, LUU V, et al. A regularization method for time-fractional linear inverse diffusion problems[J]. Electronic Journal of Differential Equations, 2016, 290: 1-18. [16] TUAN N H, HOAN L, TATAR S. An inverse problem for an inhomogeneous time-fractional diffusion equation: a regularization method and error estimate[J]. Computational & Applied Mathematics, 2019, 38(2): 1-22. [17] PODLUBNY I. Fractional Differential Equations[M]. San Diego: Academic Press, 1999. [18] VO H H, MINH T L, HONG P L, et al. An inverse problem for a time-fractional advection equation associated with a nonlinear reaction term[J]. Inverse Problems in Science & Engineering, 2021, 29(8): 1178-1198. [19] THI K T, HOANG-HUNG V. Recovering the historical distribution for nonlinear space-fractional diffusion equation with temporally dependent thermal conductivity in higher dimensional space[J]. Journal of Computational & Applied Mathematics, 2019, 345: 114-126. [20] ZHENG G H, ZHANG Q G. Recovering the initial distribution for space-fractional diffusion equation by a logarithmic regularization method[J]. Applied Mathematics Letters, 2016, 61: 143-148. doi: 10.1016/j.aml.2016.06.002 [21] ZHENG G H, ZHANG Q G. Determining the initial distribution in space-fractional diffusion by a negative exponential regularization method[J]. Inverse Problems in Science & Engineering, 2017, 25(7): 965-977. [22] IOANNIS F, MARTIN M. Fixed Point Theorems and Their Applications[M]. New York: World Scientific Publishing Company, 2013. -
计量
- 文章访问数: 794
- HTML全文浏览量: 390
- PDF下载量: 93
- 被引次数: 0
渝公网安备50010802005915号