An Element-Free Galerkin Method for Time-Fractional Diffusion-Wave Equations
-
摘要:
利用无单元Galerkin法，对Caputo意义下的时间分数阶扩散波方程进行了数值求解和相应误差理论分析。首先用L1逼近公式离散该方程中的时间变量，将时间分数阶扩散波方程转化成与时间无关的整数阶微分方程；然后采用罚函数方法处理Dirichlet边界条件，并利用无单元Galerkin法离散整数阶微分方程；最后推导该方程无单元Galerkin法的误差估计公式。数值算例证明了该方法的精度和效果。
-
关键词:
- 时间分数阶扩散波方程 /
- 无单元Galerkin法 /
- L1逼近公式 /
- 误差估计
Abstract:Numerical solution and theoretical error analysis of the element-free Galerkin (EFG) method were presented for the time-fractional diffusion-wave equations in the sense of Caputo. Through discretization of the time variables in the equation with the L1 approximate formula, the time-fractional diffusion-wave equation was transformed into a series of time-independent integer-order differential equations. Then, the penalty method was used to deal with the Dirichlet boundary condition and the EFG method was used to discretize the integer-order differential equations. Error estimates of the EFG method for the time-fractional diffusion-wave equations were derived theoretically. Finally, several numerical examples show the accuracy and effectiveness of the proposed meshless method.
-
图 1 算例1在
$ \alpha = 1.65 $ ，$ h = {1 \mathord{\left/ {\vphantom {1 {50}}} \right. } {50}} $ 和$ \tau {\text{ = }}{1 \mathord{\left/ {\vphantom {1 {40}}} \right. } {40}} $ 时的近似解和误差：(a) 近似解；(b) 误差Figure 1. Graphs of approximate solutions and resulting errors with
$ \alpha = 1.65 $ ,$ h = {1 \mathord{\left/ {\vphantom {1 {50}}} \right. } {50}} $ and$ \tau {\text{ = }}{1 \mathord{\left/ {\vphantom {1 {40}}} \right. } {40}} $ in example 1: (a) the approximate solutions; (b) the resulting errors
图 2 常数罚因子
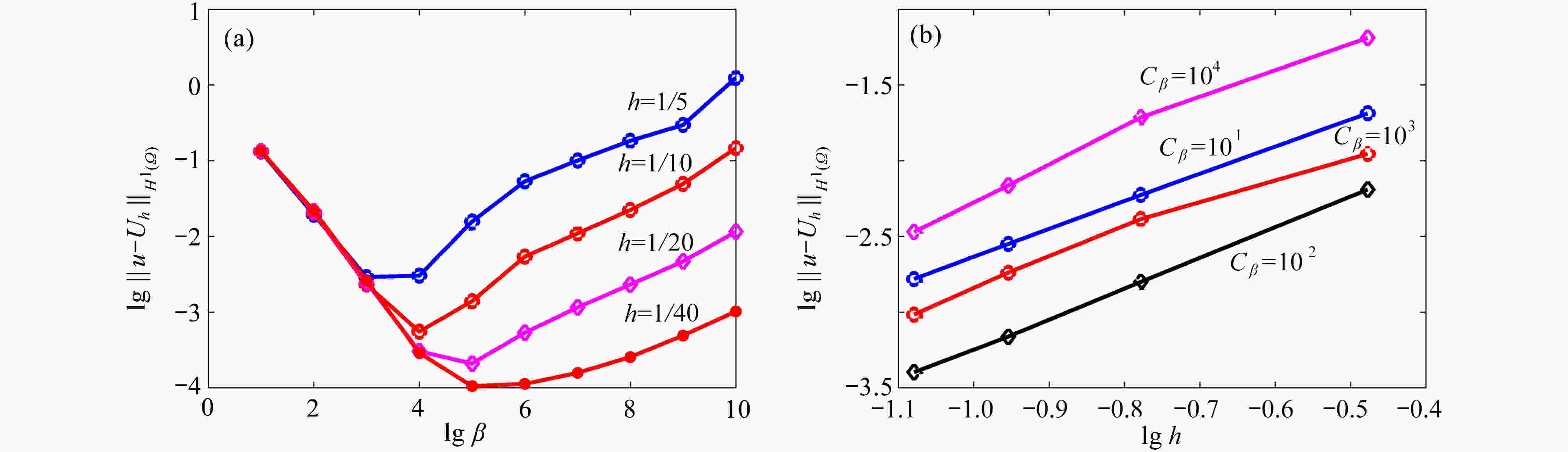
$\beta $ 和变化罚因子$ \beta = {C_\beta }{h^{ - 2}} $ 对误差和收敛性的影响：(a) 常数罚因子$\beta $ ；(b) 变化罚因子$ \beta = {C_\beta }{h^{ - 2}} $ Figure 2. The error and convergence for fixed penalty factor
$\beta $ and variable penalty factor$ \beta = {C_\beta }{h^{ - 2}} $ : (a) for fixed penalty factor$\beta $ ; (b) for variable penalty factor$ \beta = {C_\beta }{h^{ - 2}} $ 
图 3 算例1关于时间步长
$\tau $ 和空间步长$h$ 的收敛性：(a) 时间步长$\tau $ ；(b) 空间步长$h$ Figure 3. The convergence with respect to time step
$\tau $ and spatial step$h$ in example 1: (a) for time step$\tau $ ; (b) for spatial step$h$ 
图 4 影响域参数Sscale对误差的影响
Figure 4. Effects of influence domain parameter Sscale on errors
图 5 算例2关于时间步长
$\tau $ 和空间步长$h$ 的收敛性：(a) 时间步长$\tau $ ；(b) 空间步长$h$ Figure 5. The convergence with respect to time step
$\tau $ and spatial step$h$ in example 2: (a) for time step$\tau $ ; (b) for spatial step$h$ 表 1 比较有限元法和无单元Galerkin法的
$ {L_\infty } $ 误差Table 1. Comparison of
$\; {L_\infty } \;$ errors between the finite element and the element-free Galerkin methods$\alpha {\text{ = }}1.25$ $\alpha {\text{ = }}1.75$ FEM EFG FEM EFG $h ={1 / 4},\; \tau = {1 / 4}$ $5.168{\text{ }}8 \times {10^{ - 3}}$ $1.872{\text{ }}1 \times {10^{ - 3}}$ $1.088{\text{ }}5 \times {10^{ - 2}}$ $1.123{\text{ }}6 \times {10^{ - 2}}$ $h = {1 / 8}$，$\tau {\text{ = }}{1 / {64}}$ $2.261{\text{ }}6 \times {10^{ - 3}}$ $2.010{\text{ }}6 \times {10^{ - 4}}$ $2.390{\text{ }}4 \times {10^{ - 3}}$ $3.343{\text{ }}6 \times {10^{ - 4}}$ $h = {1 /{16}}$，$\tau {\text{ = }}{1 / {1{\text{ }}024}}$ $6.744{\text{ }}8 \times {10^{ - 4}}$ $4.078{\text{ }}5 \times {10^{ - 5}}$ $6.769{\text{ }}3 \times {10^{ - 4}}$ $4.078{\text{ }}5 \times {10^{ - 5}}$ $h ={1 / 8},\; \tau = {1 \mathord{\left/ {\vphantom {1 8} } \right. } 8}$ $2.479{\text{ }}5 \times {10^{ - 3}}$ $3.926{\text{ }}4 \times {10^{ - 4}}$ $6.368{\text{ }}5 \times {10^{ - 3}}$ $5.180{\text{ }}5 \times {10^{ - 3}}$ $h = {1 /{16}}$，$\tau {\text{ = }}{1 / {128}}$ $6.752{\text{ }}0 \times {10^{ - 4}}$ $4.078{\text{ }}5 \times {10^{ - 5}}$ $7.099{\text{ }}6 \times {10^{ - 4}}$ $1.507{\text{ }}3 \times {10^{ - 4}}$ 
下载: 导出CSV
表 2 比较
$ h = {{\text{π}} / {40}} $ 时，三种方法的${L_2}$ 误差Table 2. Comparison of
${L_2}$ errors obtained from 3 numerical methods with$ h = {{\text{π}} / {40}} $ $ \tau $ Galerkin FEM ADI FEM EFG ${1 / 4}$ $2.519{\text{ }}0 \times {10^{ - 1}}$ $5.451{\text{ }}2 \times {10^{ - 2}}$ $1.898{\text{ }}5 \times {10^{ - 2}}$ ${1 / 8}$ $ 2.614{\text{ }}5 \times {10^{ - 2}} $ $1.691{\text{ }}1 \times {10^{ - 2}}$ $1.179{\text{ }}1 \times {10^{ - 3}}$ ${1 / {16}}$ $8.581{\text{ }}7 \times {10^{ - 3}}$ $5.536{\text{ }}5 \times {10^{ - 3}}$ $7.670{\text{ }}7 \times {10^{ - 4}}$
下载: 导出CSV
-
[1] 孙志忠, 高广花. 分数阶微分方程的有限差分方法[M]. 2版. 北京: 科学出版社, 2021.SUN Zhizhong, GAO Guanghua. Finite Difference Methods for Fractional Differential Equations[M]. 2nd ed. Beijing: Science Press, 2021. (in Chinese) [2] 高兴华, 李宏, 刘洋. 非线性分数阶常微分方程的分段线性插值多项式方法[J]. 应用数学和力学, 2021, 42(5): 531-540. (GAO Xinghua, LI Hong, LIU Yang. A piecewise linear interpo1ation po1ynomia1 method for non1inear fractiona1 ordinary differential equations[J]. Applied Mathematics and Mechanics, 2021, 42(5): 531-540.(in Chinese) [3] SUN Z Z, WU X N. A fully discrete difference scheme for a diffusion-wave system[J]. Applied Numerical Mathematics, 2006, 56(2): 193-209. doi: 10.1016/j.apnum.2005.03.003 [4] SHEN J Y, LI C P, SUN Z Z. An H2N2 interpolation for Caputo derivative with order in (1, 2) and its application to time-fractional wave equations in more than one space dimension[J]. Journal of Scientific Computing, 2020, 83: 38. doi: 10.1007/s10915-020-01219-8 [5] FENG L B, LIU F W, TURNER I. Finite difference/finite element method for a novel 2D multi-term time-fractional mixed sub-diffusion and diffusion-wave equation on convex domains[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 70: 354-371. doi: 10.1016/j.cnsns.2018.10.016 [6] LI L M, XU D, LUO M. Alternating direction implicit Galerkin finite element method for the two-dimensional fractional diffusion-wave equation[J]. Journal of Computational Physics, 2013, 255: 471-485. doi: 10.1016/j.jcp.2013.08.031 [7] REN J C, LONG X N, MAO S P, et al. Superconvergence of finite element approximations for the fractional diffusion-wave equation[J]. Journal of Scientific Computing, 2017, 72: 917-935. doi: 10.1007/s10915-017-0385-z [8] DEHGHAN M, ABBASZADEH M, MOHEBBI A. Analysis of two methods based on Galerkin weak form for fractional diffusion-wave: meshless interpolating element free Galerkin (IEFG) and finite element methods[J]. Engineering Analysis With Boundary Elements, 2016, 64: 205-221. doi: 10.1016/j.enganabound.2015.11.011 [9] 程玉民. 无网格方法[M]. 北京: 科学出版社, 2015.CHENG Yumin. Meshless Method[M]. Beijing: Science Press, 2015. (in Chinese) [10] YANG J Y, ZHAO Y M, LIU N, et al. An implicit MLS meshless method for 2-D time dependent fractional diffusion-wave equation[J]. Applied Mathematical Modelling, 2015, 39(3/4): 1229-1240. [11] KUMAR A, BHARDWAJ A. A local meshless method for time fractional nonlinear diffusion wave equation[J]. Numerical Algorithms, 2020, 85: 1311-1334. doi: 10.1007/s11075-019-00866-9 [12] 王红, 李小林. 二维瞬态热传导问题的无单元Galerkin法分析[J]. 应用数学和力学, 2021, 42(5): 460-469. (WANG Hong, LI Xiaolin. Analysis of 2D transient heat conduction problems with the element-free Galerkin method[J]. Applied Mathematics and Mechanics, 2021, 42(5): 460-469.(in Chinese) [13] LI X L, DONG H Y. An element-free Galerkin method for the obstacle problem[J]. Applied Mathematics Letters, 2021, 112: 106724. doi: 10.1016/j.aml.2020.106724 [14] DEHGHAN M, ABBASZADEH M. Two meshless procedures: moving Kriging interpolation and element-free Galerkin for fractional PDEs[J]. Applicable Analysis, 2017, 96(6): 936-969. doi: 10.1080/00036811.2016.1167879 [15] ABBASZADEH M, DEHGHAN M. Numerical and analytical investigations for neutral delay fractional damped diffusion-wave equation based on the stabilized interpolating element free Galerkin (IEFG) method[J]. Applied Numerical Mathematics, 2019, 145: 488-506. doi: 10.1016/j.apnum.2019.05.005 [16] LI X L, LI S L. On the stability of the moving least squares approximation and the element-free Galerkin method[J]. Computers and Mathematics With Applications, 2016, 72(6): 1515-1531. doi: 10.1016/j.camwa.2016.06.047 [17] LI X L. Three-dimensional complex variable element-free Galerkin method[J]. Applied Mathematical Modelling, 2018, 63: 148-171. doi: 10.1016/j.apm.2018.06.040 [18] SINGH R, SINGH K M. Interpolating meshless local Petrov-Galerkin method for steady state heat conduction problem[J]. Engineering Analysis With Boundary Elements, 2019, 101: 56-66. doi: 10.1016/j.enganabound.2018.12.012 -
计量
- 文章访问数: 864
- HTML全文浏览量: 357
- PDF下载量: 76
- 被引次数: 0
渝公网安备50010802005915号