Study of Movement Mechanisms of Droplets in Power-Law Fluids in T-Junction Microchannels With the Lattice Boltzmann Method
-
摘要:
采用非Newton不可压两相流格子Boltzmann模型研究了T型微通道内Newton液滴在非Newton幂律流体中的运动过程。研究了非Newton流体幂律指数n、主管道毛细数Ca、两相流量比Q、两相黏度比M以及主管道壁面润湿性θ对液滴在T型微通道内的形成尺寸、形成时间和变形参数(DI)的影响。研究结果表明：首先，主管道流体幂律指数n从0.4增加到1.6时，液滴的形成尺寸近似呈线性减小，而液滴的形成时间和变形参数先快速减小，然后缓慢减小；其次，黏度比对液滴形成尺寸、液滴形成以及变形参数的影响与幂律指数的影响基本一致；再者，随着Ca和主管道壁面润湿性的增加，形成液滴的尺寸近似呈线性减小，形成液滴的时间和变形参数先快速减小然后缓慢减小，且减小趋势随幂律指数的增加而减缓；最后，研究结果还表明主管道和子管道的流量比Q越大，液滴形成时间越长，液滴形成尺寸和变形参数越小。
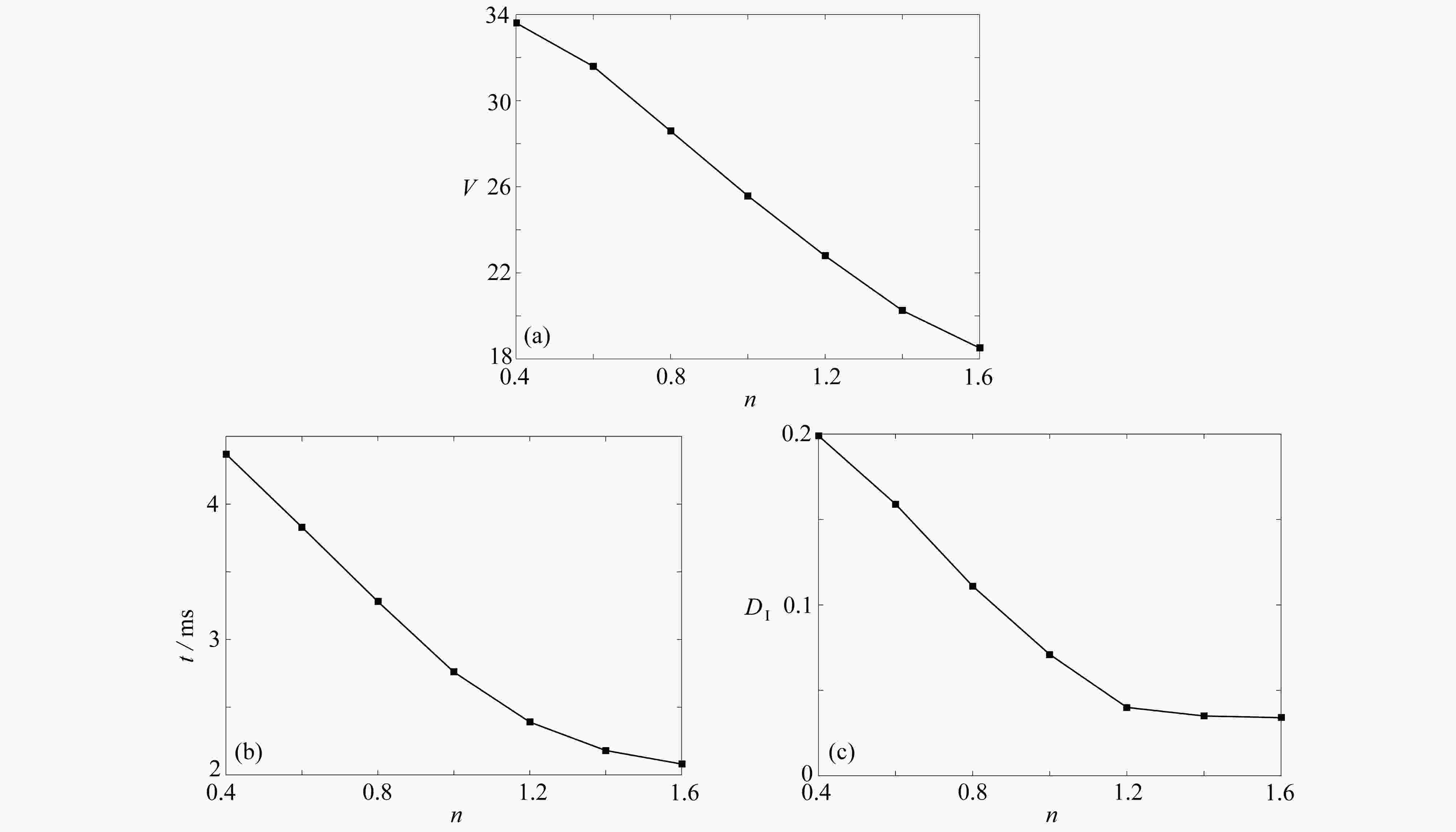
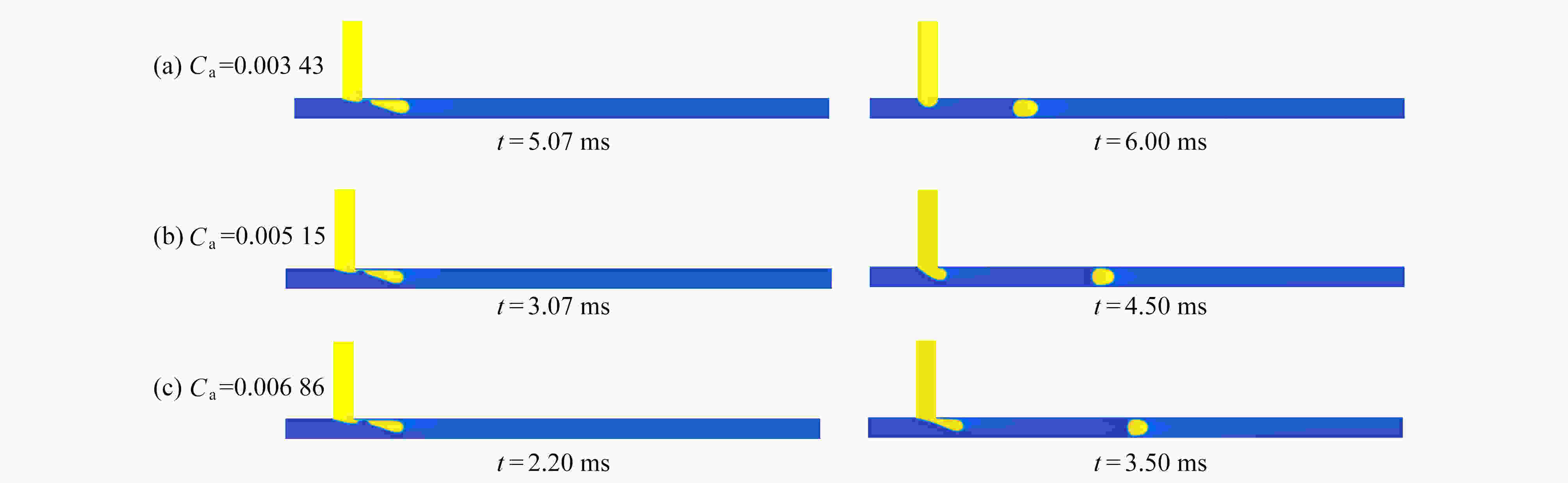
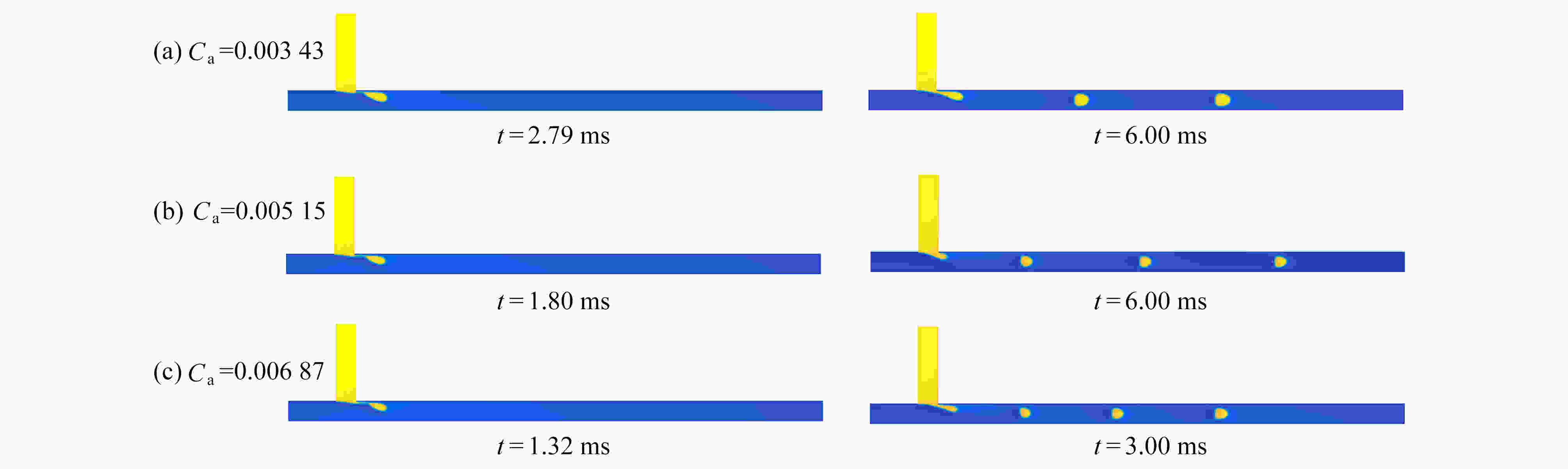
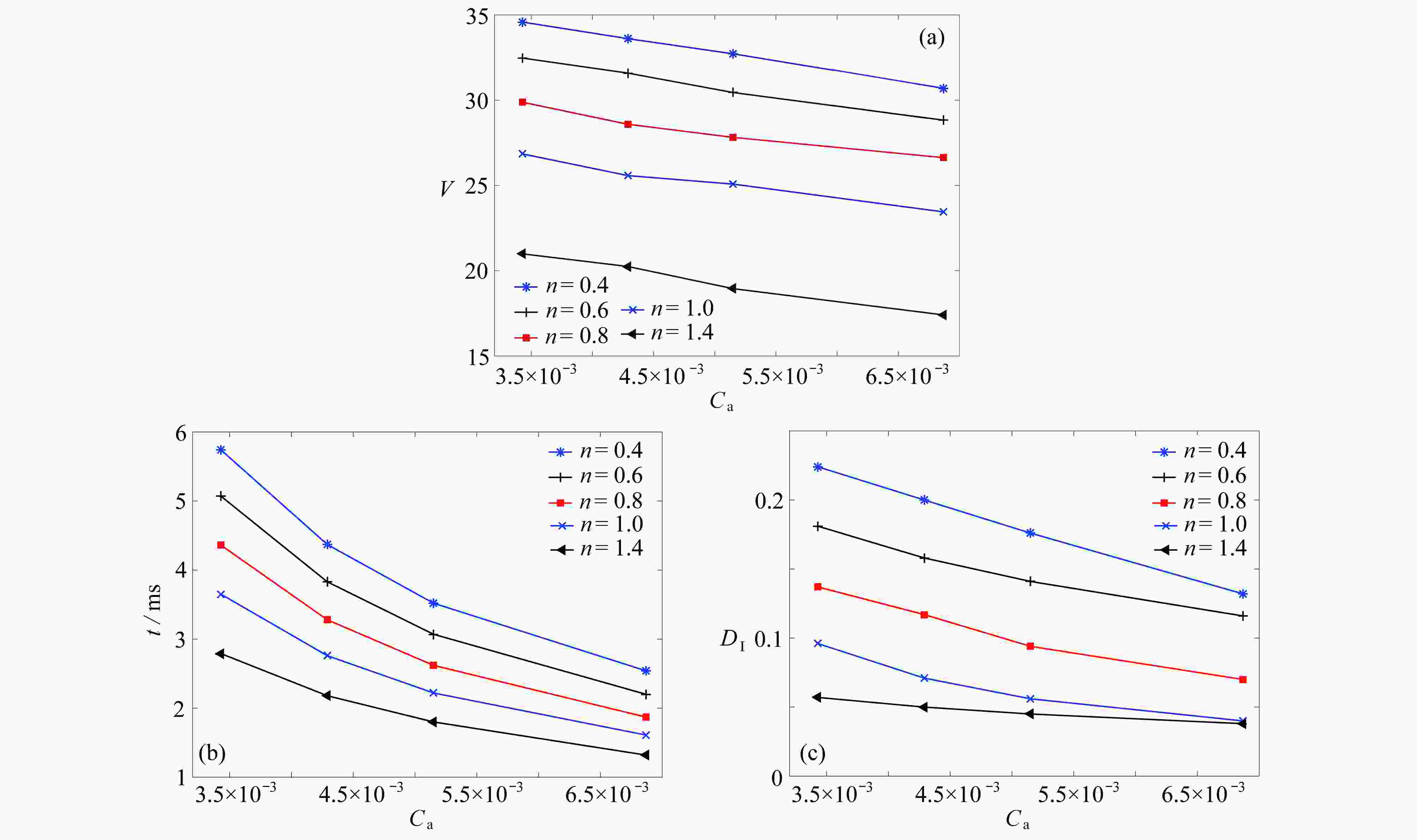
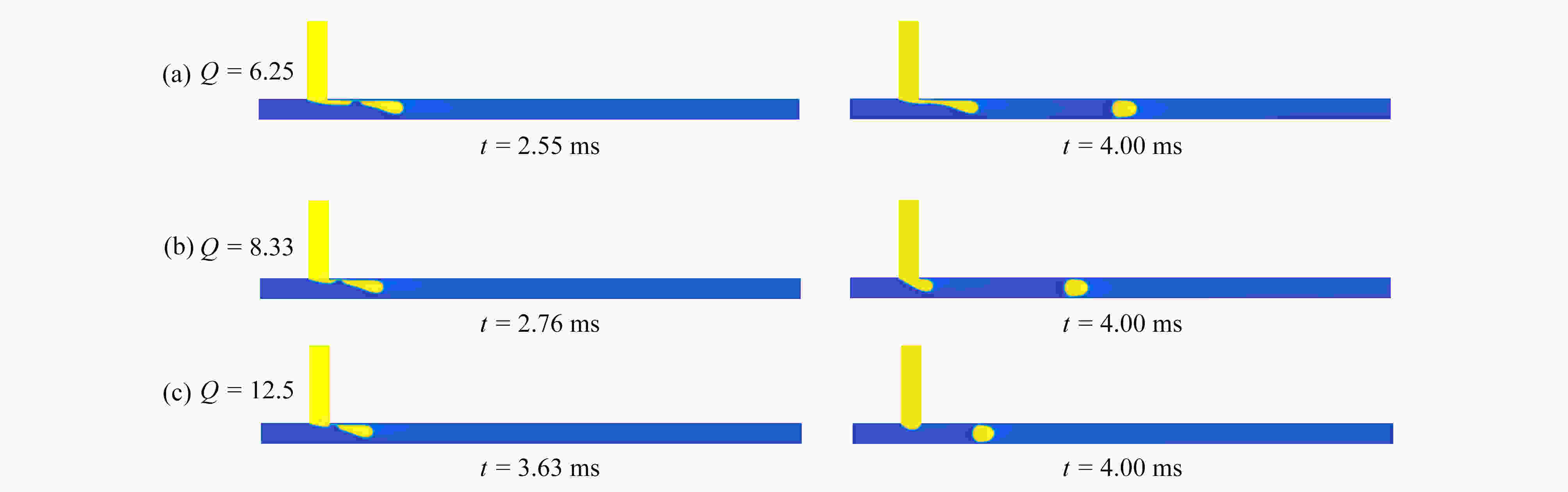
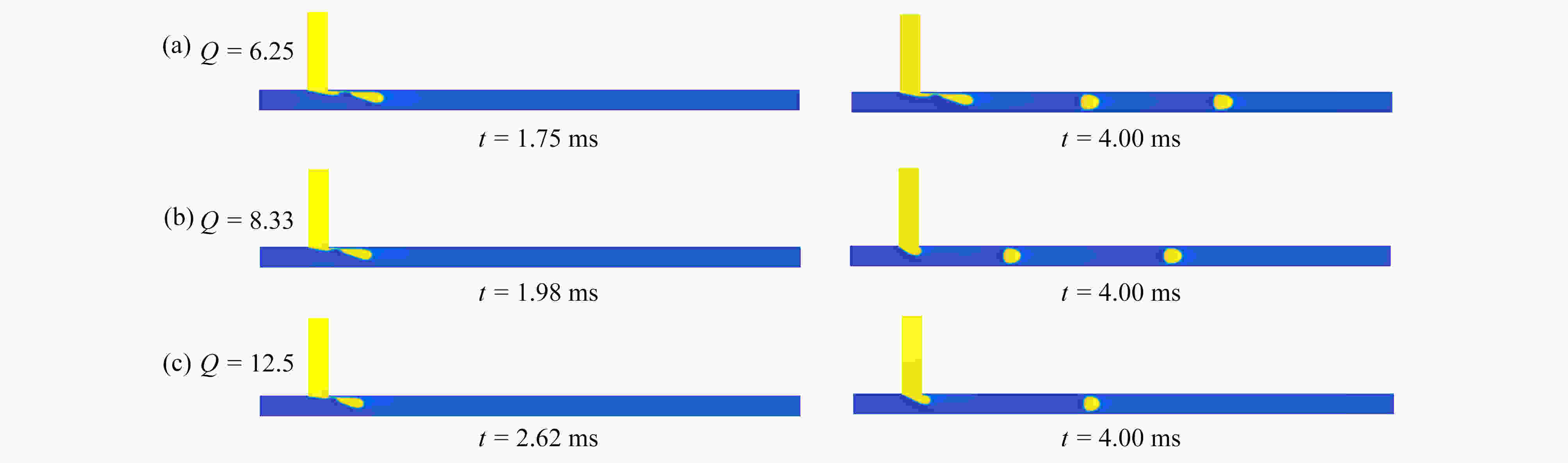
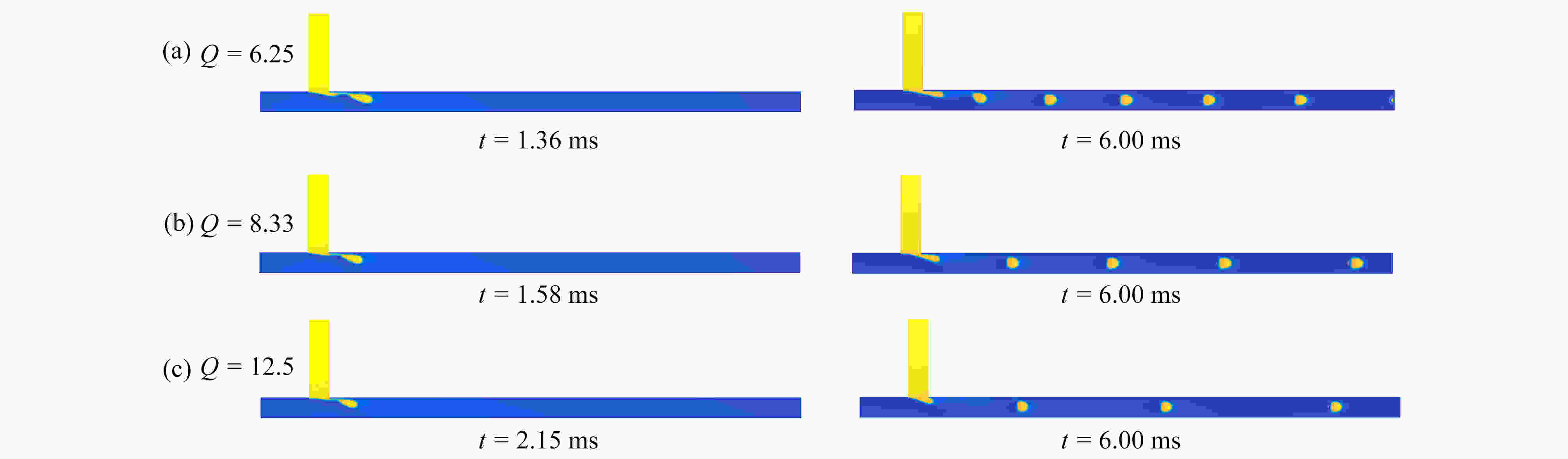
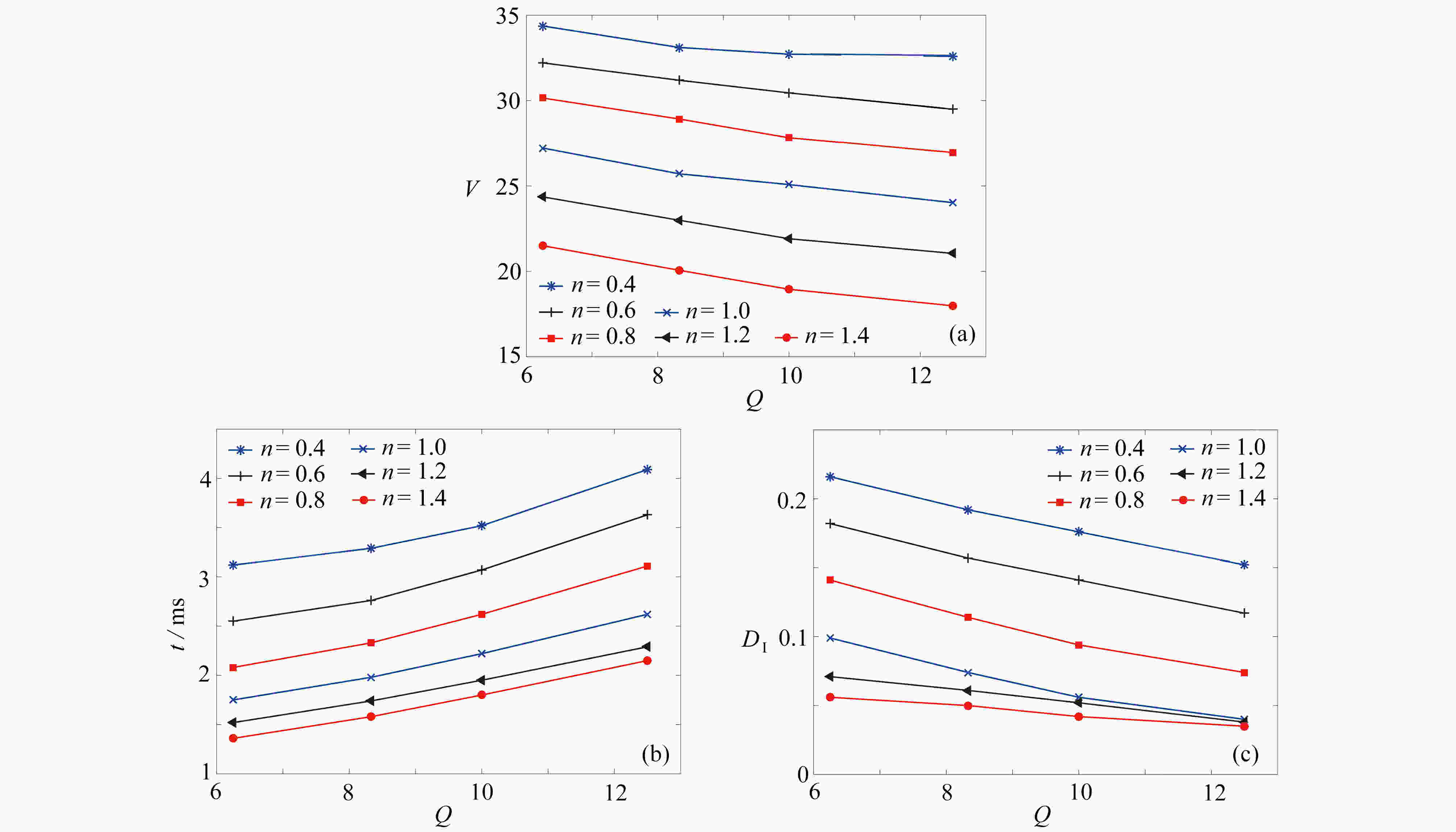
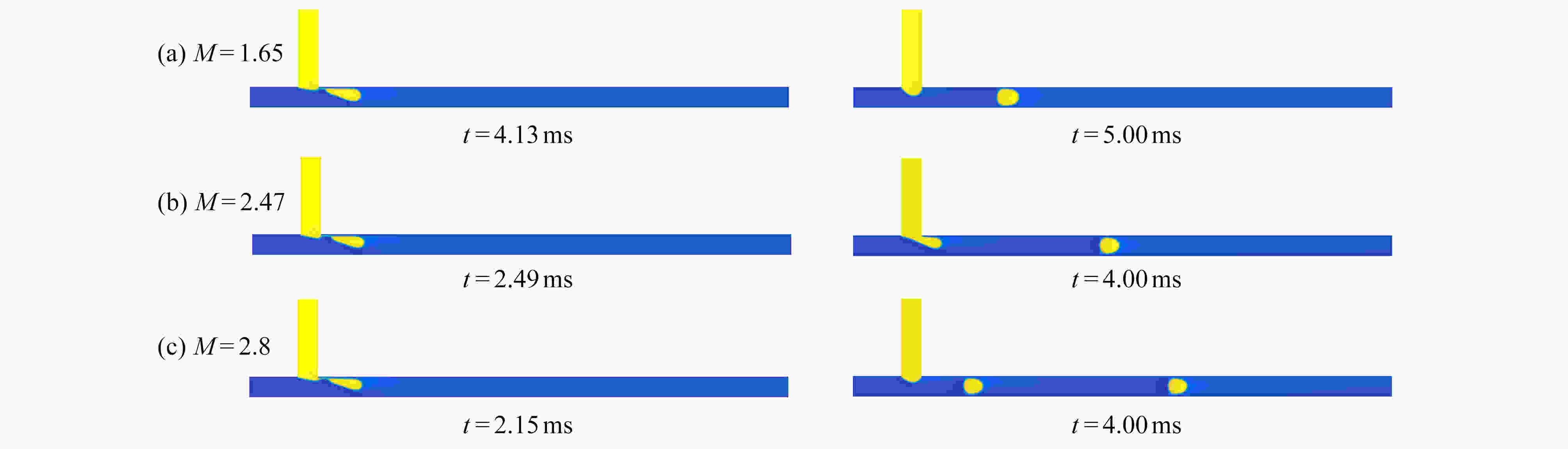
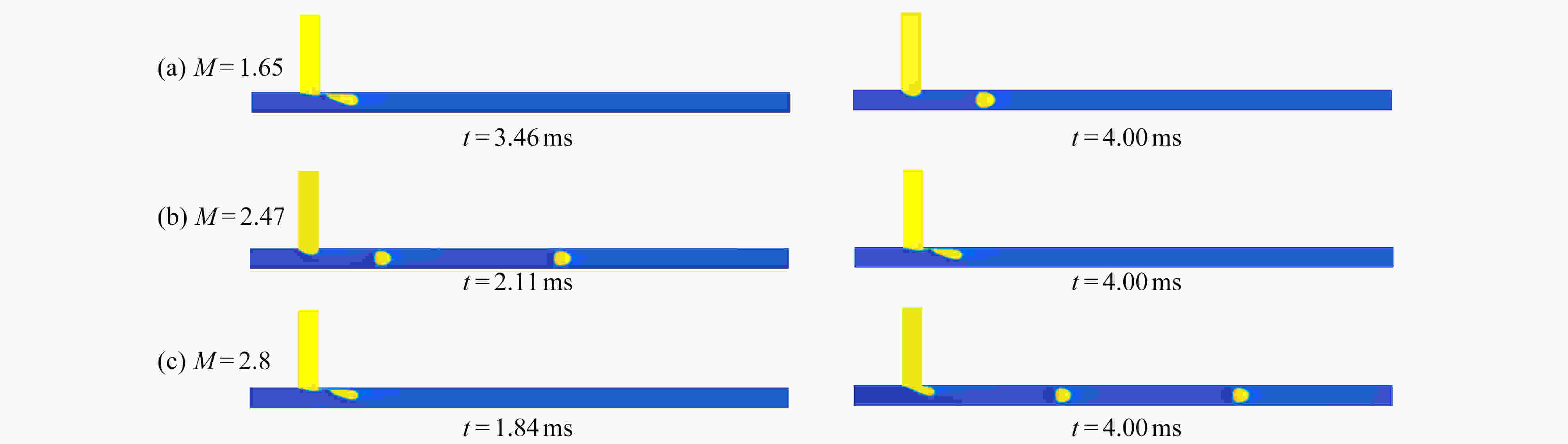
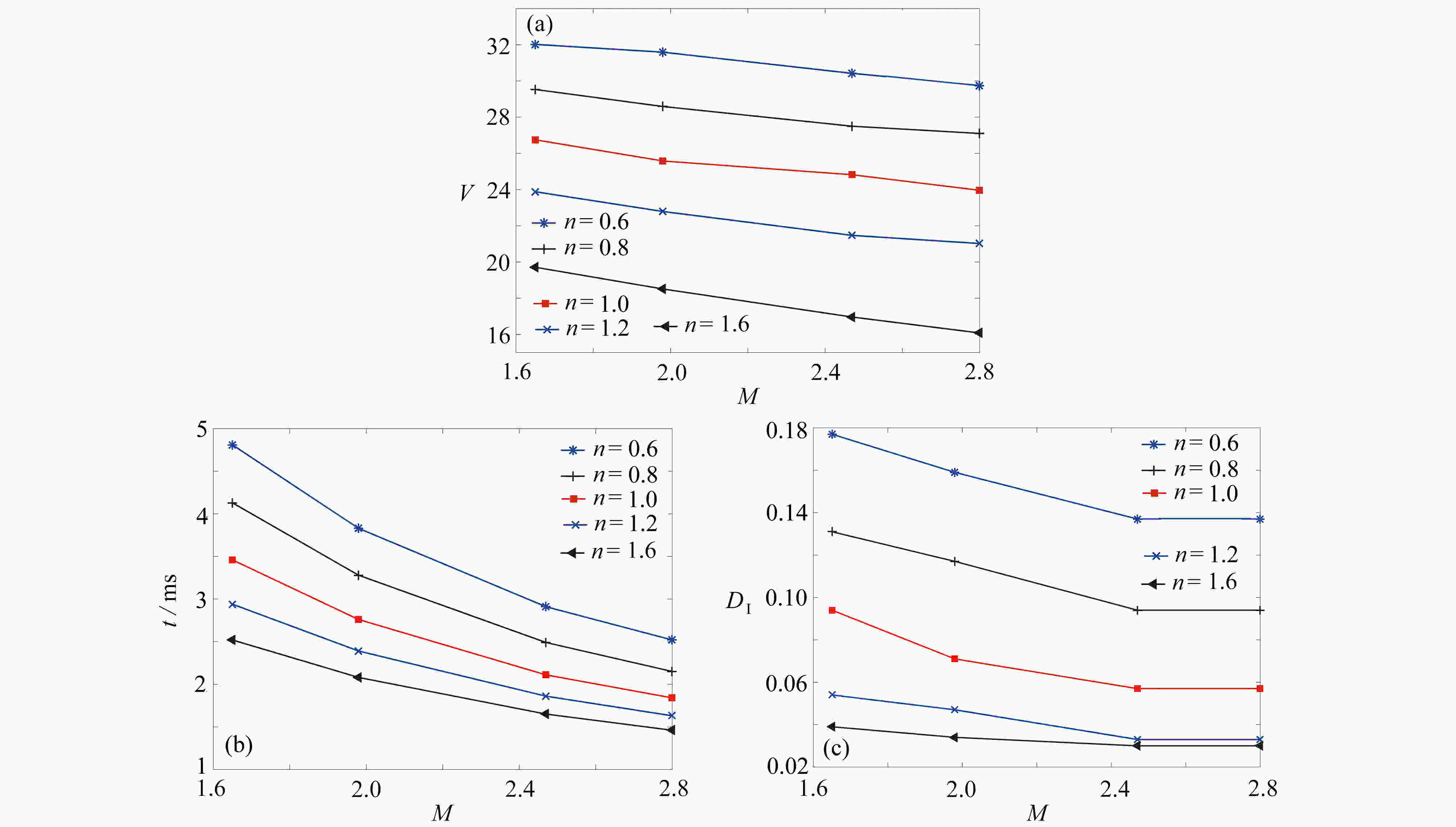
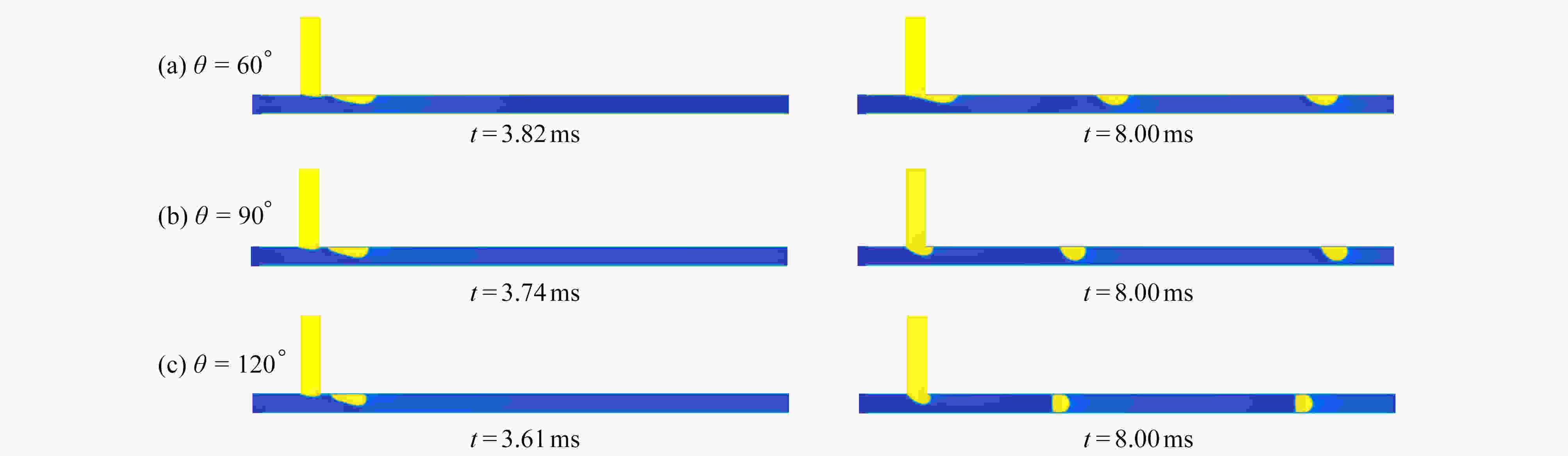
Abstract:The movement mechanisms of Newtonian droplets in power-law fluids in T-junction microchannels were studied with the lattice Boltzmann method. The effects of power-law index n , capillary number Ca , flow ratio Q , viscosity ratio M, and surface wettability θ on the droplet formation size, the formation time and the deformation index (DI) were investigated in detail. The results show that, first, with the increase of power-law index n from 0.4 to 1.6, the droplet formation size decreases almost linearly, and both the droplet formation time and the deformation index decrease quickly at first and then much more slowly. Second, the influences of the viscosity ratio on the droplet formation size, the formation time and the deformation index are basically the same as those of the power law index. In addition, with the increases of Ca and θ of the main channel, the droplet formation size decreases almost linearly, while the droplet formation time and deformation index decrease rapidly at first and then slowly, and the decreasing rates weaken with the increase of the power-law index. At last, with the increase of flow ratio Q of the continuous phase over the dispersed phase, the droplet formation size increases, and the droplet formation time as well as the deformation index decrease.
-
图 1 液滴内外压力差∆P和半径倒数1/r之间的关系
Figure 1. Relationships between pressure jump across the droplet interface ∆P and inverse of droplet radius 1/r
图 2 不同静态接触角θeq得到的稳态接触角
Figure 2. Steady state contact angles obtained with different values of static contact angle θeq
图 4 不同幂律指数下，液滴的变形参数DI与Ca的关系
Figure 4. Deformation parameter DI as a function of the capillary number for different power-law fluids
图 6 T型微通道内主管道流体不同幂律指数液滴形成过程
Figure 6. The droplet formation process of the continuous phase fluid with different power-law indexes in the T-junction microchannel
图 7 主管道流体幂律指数n对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数
Figure 7. The effects of continuous phase power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index
图 8 主管道流体为剪切变稀流体(n=0.6)时，不同Ca下的T型微通道内液滴形成过程
Figure 8. The droplet formation process in the T-junction microchannel obtained with different capillary numbers for a shear thinning continuous phase fluid (n=0.6)
图 9 主管道流体为Newton流体(n=1.0)时，不同Ca下的T型微通道内液滴形成过程
Figure 9. The droplet formation process in the T-junction microchannel obtained with different capillary numbers for a Newtonian continuous phase fluid (n=1.0)
图 10 主管道流体为剪切变稠流体(n=1.4)时，不同Ca下的T型微通道内液滴形成过程
Figure 10. The droplet formation process in the T-junction microchannel obtained with different capillary numbers for a shear thickening continuous phase fluid (n=1.4)
图 11 主管道Ca和幂律指数n对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数
Figure 11. The effects of continuous phase capillary number Ca and power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index
图 12 主管道流体为剪切变稀流体(n=0.6)时，在不同流量比Q得到的T型微通道内液滴形成过程
Figure 12. The droplet formation process in the T-junction microchannel obtained with different flow ratios Q for a shear thinning continuous phase fluid (n=0.6)
图 13 主管道流体为Newton流体(n=1.0)时，不同流量比Q得到的T型微通道内液滴形成过程
Figure 13. The droplet formation process in the T-junction microchannel obtained with different flow ratios Q for a Newtonian continuous phase fluid (n=1.0)
图 14 主管道流体为剪切变稠流体(n=1.4)时，不同流量比Q得到的T型微通道内液滴形成过程
Figure 14. The droplet formation process in the T-junction microchannel obtained with different flow ratios Q for a shear thickening continuous phase fluid (n=1.4)
图 15 流量比Q和幂律指数n对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数
Figure 15. The effects of continuous phase flow ratio Q and power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index
图 16 主管道流体为剪切变稀流体(n=0.8)时，不同M得到的T型微通道内液滴形成过程
Figure 16. The droplet formation process in the T-junction microchannel obtained with different viscosity ratios M for a shear thinning continuous phase fluid (n=0.8)
图 17 主管道流体为Newton流体(n=1.0)时，不同M得到的T型微通道内液滴形成过程
Figure 17. The droplet formation process in the T-junction microchannel obtained with different viscosity ratios M for a Newtonian continuous phase fluid (n=1.0)
图 18 主管道流体为剪切变稠流体(n=1.2)时，不同M得到的T型微通道内液滴形成过程
Figure 18. The droplet formation process in the T-junction microchannel obtained with different viscosity ratios M for a shear thickening continuous phase fluid (n=1.2)
图 19 黏度比M和幂律指数n对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数
Figure 19. The effects of continuous phase viscosity ratio M and power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index
图 20 主管道流体为剪切变稀(n=0.8)时，不同壁面润湿性θ得到的T型微通道内液滴形成过程
Figure 20. The droplet formation process in the T-junction microchannel obtained with different surface wettabilities θ for a shear thinning continuous phase fluid (n=0.8)
21 主管道流体为Newton流体(n=1.0)时，不同壁面润湿性θ得到的T型微通道内液滴形成过程
21. The droplet formation process in the T-junction microchannel obtained with different surface wettabilities θ for a Newtonian continuous phase fluid (n=1.0)
图 22 主管道流体为剪切变稠流体(n=1.2)时，不同壁面润湿性得到的T型微通道内液滴形成过程
Figure 22. The droplet formation process in the T-junction microchannel obtained with different surface wettabilities θ for a shear thickening continuous phase fluid (n=1.2)
-
[1] GANAN-CALVO A M, MONTANERO J M, MARTIN-BANDERAS L, et al. Building functional materials for health care and pharmacy from microfluidic principles and flow focusing[J]. Advanced Drug Delivery Reviews, 2013, 65(11/12): 1447-1469. [2] MATULA K, RIVELLO F, HUCK WILHELM T S. Single-cell analysis using droplet microfluidics[J]. Advanced Biosystems, 2020, 4: 1900188. doi: 10.1002/adbi.201900188 [3] YAN L F, WANG H, BAI L, et al. Suzuki-Miyura cross-coupling reaction in droplet-based microreactor[J]. Chemical Engineering Science, 2019, 207: 352-357. doi: 10.1016/j.ces.2019.06.031 [4] ZHAO N, LONG W, HE Y Q. Dynamic behavior and driving force model of droplet formation in a T-junction microchannel[J]. Journal of Micromechanics and Microengineering, 2019, 29: 115002. doi: 10.1088/1361-6439/ab38f5 [5] HAN W B, CHEN X Y. Numerical simulation of the droplet formation in a T-junction microchannel by a level-set method[J]. Australian Journal of Chemistry, 2018, 71(12): 957-964. doi: 10.1071/CH18320 [6] LI X, HE L, GU H, et al. Numerical study of droplet formation in the T-junction microchannel with wall velocity slip[J]. Energy Procedia, 2019, 158: 5459-5464. doi: 10.1016/j.egypro.2019.01.601 [7] SHI Y, TANG G H, XIA H H. Lattice Boltzmann simulation of droplet formation in T-junction and flow focusing devices[J]. Computers and Fluids, 2014, 90: 155-163. doi: 10.1016/j.compfluid.2013.11.025 [8] LIU H H, ZHANG Y H. Droplet formation in a T-shaped microfluidic junction[J]. Journal of Applied Physics, 2009, 106(3): 034906. [9] FALLAH K, TAEIBI M. Lattice Boltzmann simulation of drop formation in T-junction microchannel[J]. Journal of Molecular Liquids, 2017, 240: 723-732. doi: 10.1016/j.molliq.2017.05.108 [10] GLAWDEL T, ELBUKEN C, REN C L. Droplet formation in microfluidic T-junction generators operating in the transitional regime Ⅱ: modeling[J]. Physical Review E, 2012, 85(1/2): 016323. [11] FU T T, WEI L J, ZHU C Y, et al. Flow patterns of liquid-liquid two-phase flow in non-Newtonian fluids in rectangular microchannels[J]. Chemical Engineering and Processing Process Intensification, 2015, 91: 114-120. doi: 10.1016/j.cep.2015.03.020 [12] 黄一帆, 娄钦. T型微通道内的幂律流体液滴破裂行为的格子Boltzmann方法模拟[J]. 应用数学和力学, 2020, 41(10): 1125-1145. (HUANG Yifan, LOU Qin. Power-law fluid droplet dynamic behaviors in T-junction micro-channels with the lattice Boltzmann method[J]. Applied Mathematics and Mechanics, 2020, 41(10): 1125-1145.(in Chinese) [13] SANG L, HONG Y P, WANG F J. Investigation of viscosity effect on droplet formation in T-shaped microchannels by numerical and analytical methods[J]. Microfluid and Nanofluid, 2009, 6: 621-635. doi: 10.1007/s10404-008-0329-x [14] SONTTI S G, ATTA A. CFD analysis of microfluidic droplet formation in non-Newtonian liquid[J]. Chemical Engineering Journal, 2017, 330: 245-261. doi: 10.1016/j.cej.2017.07.097 [15] CHIARELLO E, GUPTA A, MISTURA G, et al. Droplet breakup driven by shear thinning solutionsin a microfluidic T-junction[J]. Physical Review E, 2017, 2: 123602. [16] GUPTA A, SBRAGAGLIA M. Effects of viscoelasticity on droplet dynamics and break-up inmicrofluidic T-junctions: a lattice Boltzmann study[J]. The European Physical Journal E, 2016, 39: 6. doi: 10.1140/epje/i2016-16006-9 [17] SHI Y, TANG G H. Lattice Boltzmann simulation of droplet formation in non-Newtonian fluids[J]. Communications in Computational Physics, 2015, 17: 1056-1072. doi: 10.4208/cicp.2014.m333 [18] CHAI Z H, SHI B C, GUO Z L. A multiple-relaxation-time lattice Boltzmann model for general nonlinear anisotropic convection-diffusion equations[J]. Journal of Scientific Computing, 2016, 69: 355-390. doi: 10.1007/s10915-016-0198-5 [19] GUO Z L. Well-balanced lattice Boltzmann model for two-phase systems[J]. Physics of Fluids, 2021, 33: 031709. doi: 10.1063/5.0041446 [20] 梁宏, 柴振华, 施保昌. 分叉微通道内液滴动力学行为的格子Boltzmann方法模拟[J]. 物理学报, 2016, 65(20): 139-148. (LIANG Hong, CHAI Zhenhua, SHI Baochang. Lattice Boltzmann simulation of droplet dynamics in a bifurcating micro-channel[J]. Journal of Physics, 2016, 65(20): 139-148.(in Chinese) [21] 李梦军, 戴厚平, 魏雪丹, 等. 空间分数阶电报方程的格子Boltzmann方法[J]. 应用数学和力学, 2021, 42(5): 522-530. (LI Mengjun, DAI Houping, WEI Xuedan, et al. A lattice Boltzmann method for spatial fractional-order telegraph equations[J]. Applied Mathematics and Mechanics, 2021, 42(5): 522-530.(in Chinese) [22] LOU Q, HUANG Y F, LI L. Lattice Boltzmann model of gas-liquid two-phase flow of incomprssible power-law fluid and its application in the displacement problem of porous media[J]. Acta Physica Sinica, 2019, 68(21): 214702. doi: 10.7498/aps.68.20190873 [23] YUAN P, SCHAEFER L. Equations of state in a lattice Boltzmann model[J]. Physics of Fluids, 2006, 18(4): 042101. doi: 10.1063/1.2187070 [24] GUO Z L, ZHENG C G, SHI B C. Force imbalance in lattice Boltzmann equation for two-phase flows[J]. Physical Review E, 2011, 83: 036707. doi: 10.1103/PhysRevE.83.036707 [25] DAVIES A R, SUMMERS J L, WILSON M C T. On a dynamic wetting model for the finite-density multiphase lattice Boltzmann method[J]. International Journal of Computational Fluid Dynamics, 2006, 20(6): 415-425. doi: 10.1080/10618560601000777 [26] LOU Q, YANG M, XU H T. Wetting boundary condition in an improved lattice Boltzmann method for nonideal gases[J]. Communications in Computational Physics, 2018, 23(4): 1116-1130. [27] WIKLUND H S, LINDSTROM S B, UESAKA T. Boundary condition considerations in lattice Boltzmann formulations of wetting binary fluids[J]. Computer Physics Communications, 2011, 182(10): 2192-2200. doi: 10.1016/j.cpc.2011.05.019 [28] WANG N N, LIU H H, ZHANG C H. Deformation and breakup of a confined droplet in shear flows with power-law rheology[J]. Journal of Rheology, 2017, 61(4): 741-758. doi: 10.1122/1.4984757 [29] LADD A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation part Ⅰ: theoretical foundation[J]. Journal of Fluid Mechanics, 1994, 271: 285-310. doi: 10.1017/S0022112094001771 [30] LOU Q, GUO Z L, SHI B C. Evaluation of outflow boundary conditions for two-phase lattice Boltzmann equation[J]. Physical Review E, 2013, 87: 063301. doi: 10.1103/PhysRevE.87.063301 -
下载:
计量
- 文章访问数: 734
- HTML全文浏览量: 395
- PDF下载量: 59
- 被引次数: 0
渝公网安备50010802005915号