A Modified Multi-Splitting Iterative Method With the Restarted GMRES to Solve the PageRank Problem
-
摘要:
PageRank算法已经成为网络搜索引擎的核心技术。针对PageRank问题导出的线性方程组，首先将Krylov子空间方法中的重启GMRES(generalized minimal residual)方法与多分裂迭代(multi-splitting iteration，MSI)方法相结合，提出了一种重启GMRES修正的多分裂迭代法；然后，给出了该算法的详细计算流程和收敛性分析；最后，通过数值实验验证了该算法的有效性。
Abstract:The PageRank algorithm has become the core technology for web search engines. For the linear equations derived from the PageRank problem, firstly, the restarted GMRES (generalized minimal residual) method of the Krylov subspace methods was combined with the multi-splitting iterative method, and a modified multi-splitting iterative method with the restarted GMRES was proposed. Then, the detailed calculating process and the convergence analysis of this new algorithm were given. Finally, the effectiveness of the algorithm was demonstrated through some numerical experiments.
-
Key words:
- PageRank /
- restarted GMRES /
- multi-splitting iterative method /
- convergence
-
图 2 重启GMRES-MSI方法的计算流程图
Figure 2. The calculation flow chart for the restarted GMRES-MSI method
图 3
$\alpha$ 取不同值时, 3种方法计算zkyG矩阵的收敛曲线图Figure 3. For different
$\alpha$ values, the convergence curves of the zkyG matrix with the 3 methods
图 4
$\alpha$ 取不同值时, 3种方法计算Email-Enron矩阵的收敛曲线图Figure 4. For different
$\alpha$ values, the convergence curves of the Email-Enron matrix with the 3 methods
图 5
$\alpha$ 取不同值时, 3种方法计算web-Stanford矩阵的收敛曲线图Figure 5. For different
$\alpha$ values, the convergence curves of the web-Stanford matrix with the 3 methods表 1 网络矩阵的性质
Table 1. The nature of the network matrix
name dimension nonzeros average nonzeros zkyG 5000 95935 19.2 Email-Enron 36692 367662 10.0 web-Stanford 281903 2312497 8.2 
下载: 导出CSV
表 2 ZkyG矩阵
Table 2. The zkyG matrix
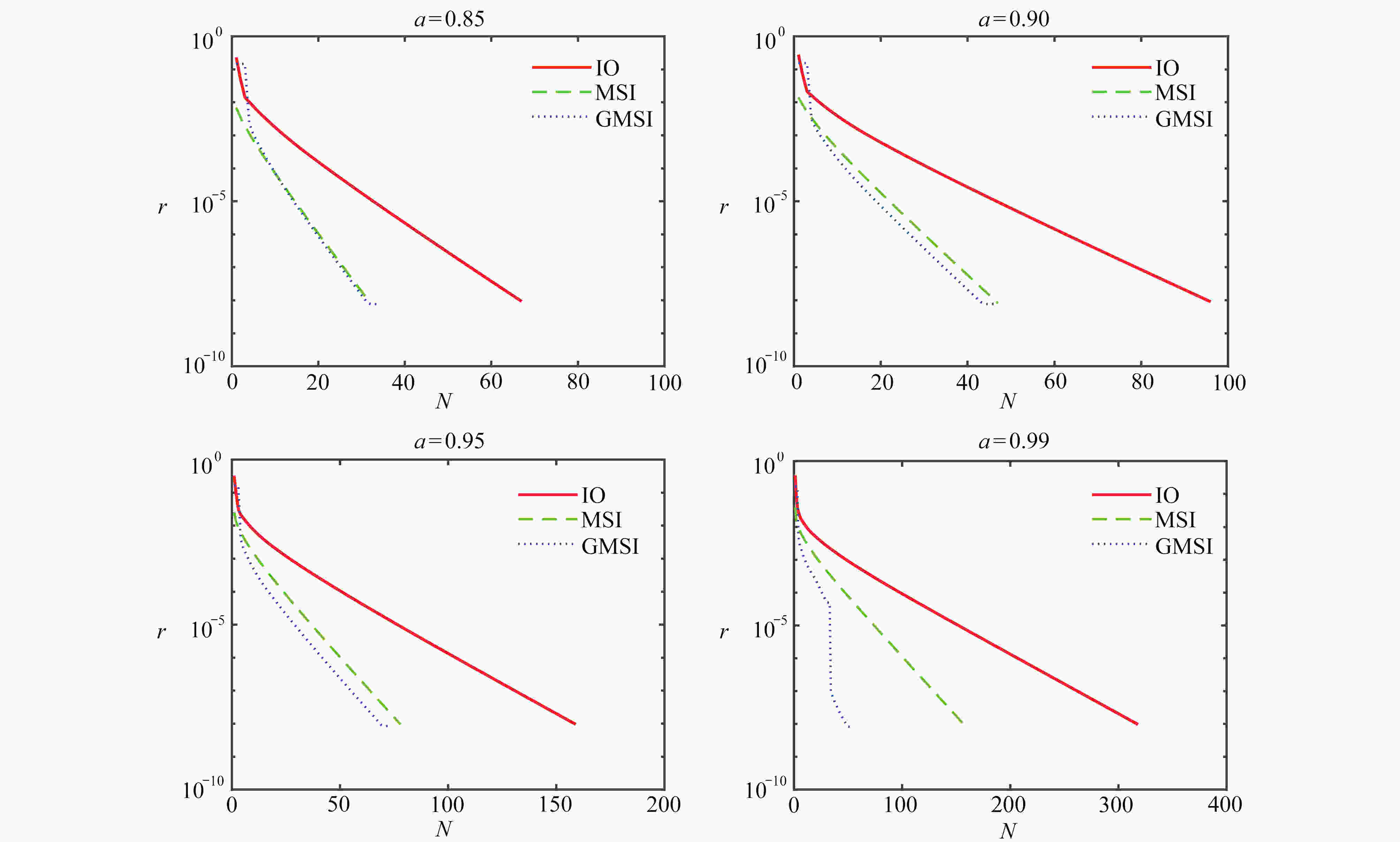
$\alpha$ N T/s $\delta/\text{%}$ IO MSI GMSI IO MSI GMSI 0.850 67 32 34 0.0131 0.0128 0.0125 2.34 0.900 96 47 46 0.0188 0.0180 0.0173 3.89 0.950 159 78 72 0.0281 0.0263 0.0250 4.94 0.990 318 157 52 0.0519 0.0509 0.0285 44.01 0.993 343 170 56 0.0562 0.0558 0.0323 42.11 0.995 362 179 59 0.0579 0.0565 0.0332 41.24 0.998 395 196 62 0.0678 0.0623 0.0361 42.05
下载: 导出CSV
表 3 Email-Enron矩阵
Table 3. The Email-Enron matrix
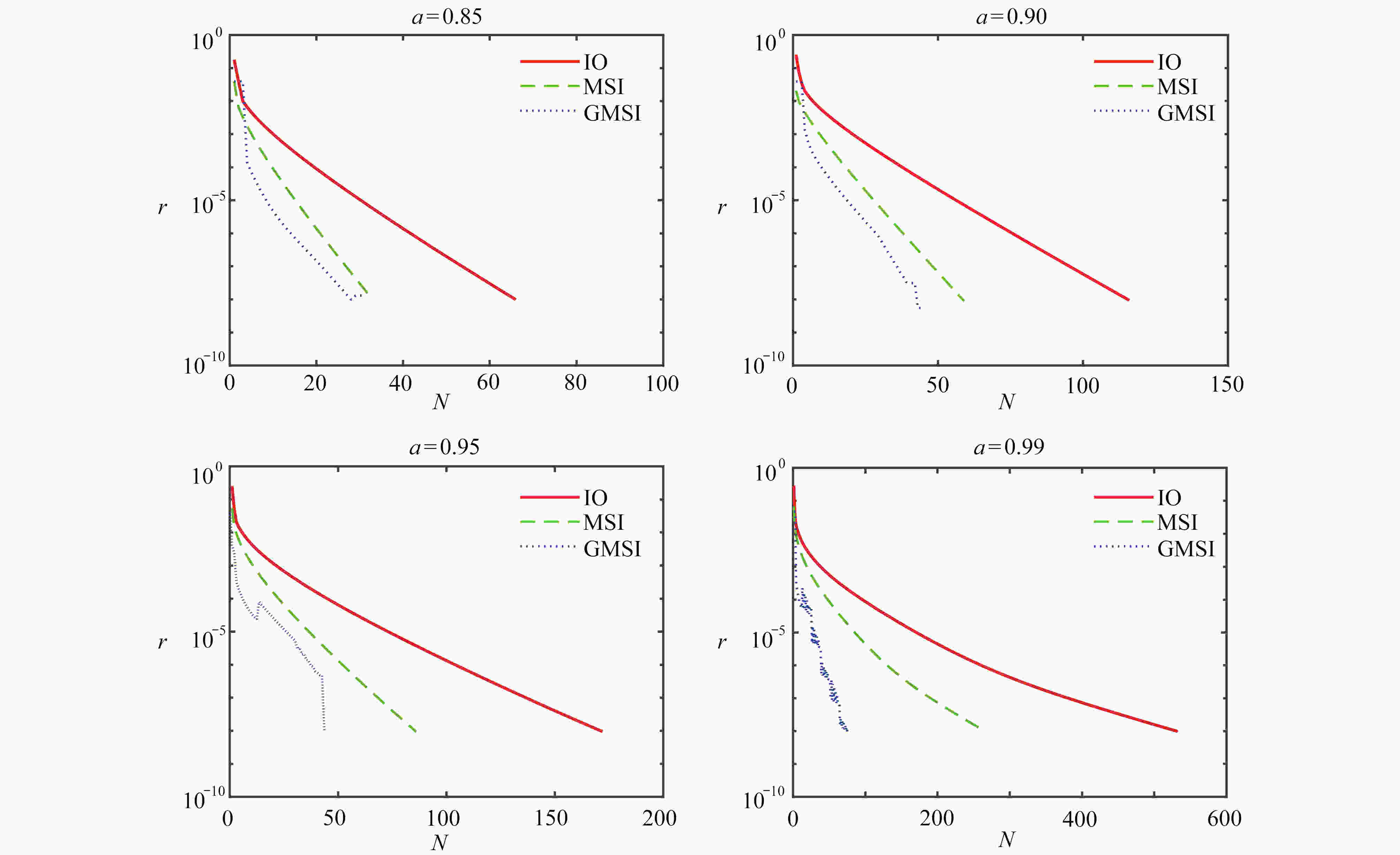
$\alpha$ N T/s $\delta/\text{%}$ IO MSI GMSI IO MSI GMSI 0.850 66 33 31 0.0944 0.0940 0.0920 2.10 0.900 97 49 44 0.1513 0.1443 0.1363 5.54 0.950 172 86 43 0.3065 0.2039 0.1492 26.83 0.990 532 266 77 0.7435 0.6248 0.3147 49.63 0.993 672 336 83 0.8011 0.7794 0.3501 55.08 0.995 814 407 93 0.9847 0.9293 0.4121 55.65 0.998 1197 599 103 1.4537 1.3445 0.4353 67.62
下载: 导出CSV
表 4 Web-Stanford矩阵
Table 4. The web-Stanford matrix
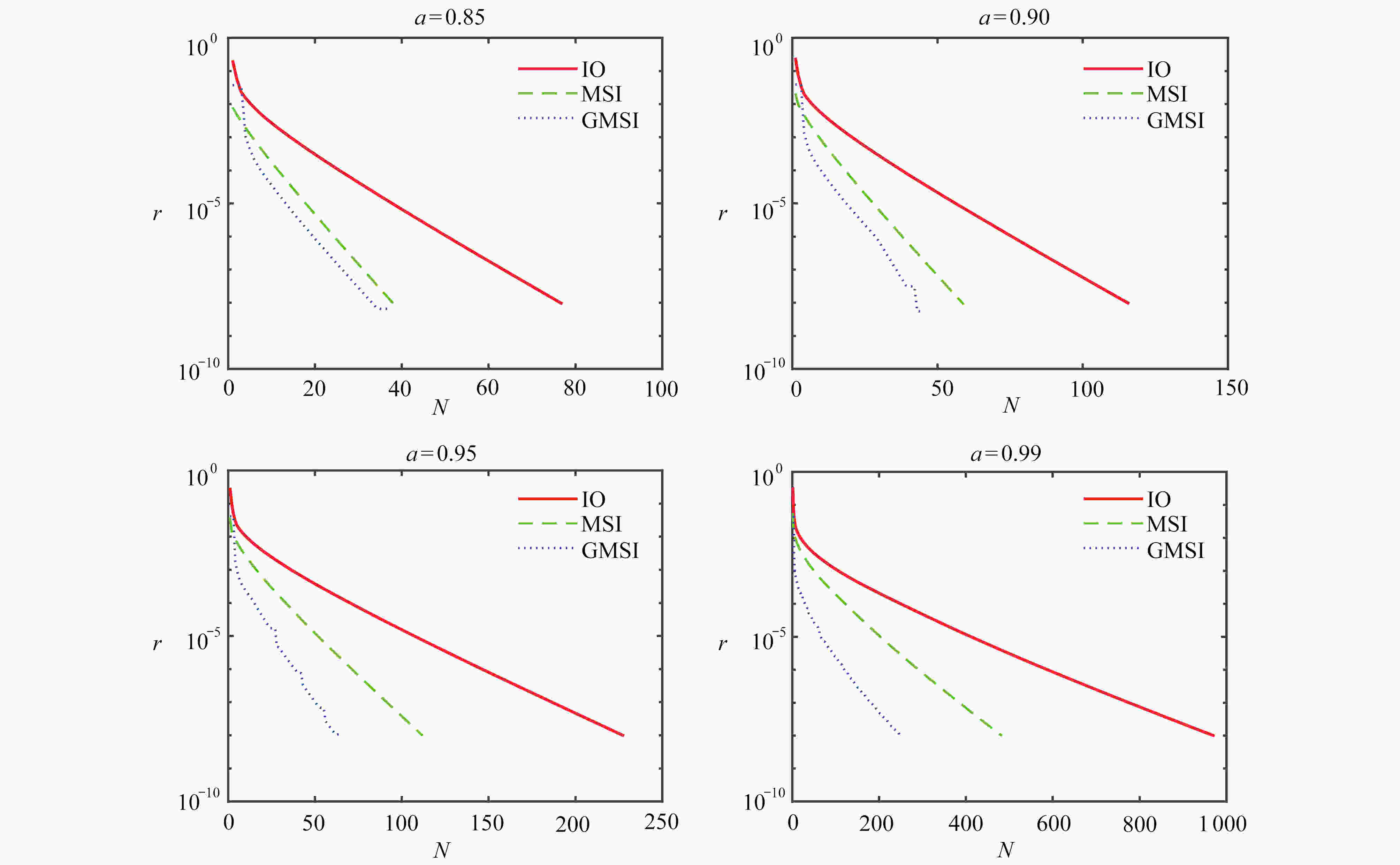
$\alpha$ N T/s $\delta/\text{%}$ IO MSI GMSI IO MSI GMSI 0.850 77 38 37 9.6007 9.6721 9.3090 3.75 0.900 116 59 45 14.4223 14.8708 11.8362 20.41 0.950 228 112 65 19.9523 19.4775 14.9663 23.16 0.990 971 483 253 80.2277 78.9326 56.7893 28.05 0.993 1323 658 304 108.1148 107.3698 66.0350 38.50 0.995 1763 878 396 144.9783 142.5481 90.1826 36.74 0.998 3689 1 844 955 329.9754 317.1118 207.9194 34.43
下载: 导出CSV
-
[1] BRIN S, PAGE L. The anatomy of a large-scale hypertextual web search engine[J]. Computer Networks and ISDN Systems, 1998, 30: 107-117. doi: 10.1016/S0169-7552(98)00110-X [2] KAMVAR S D, HAVELIWALA T H, MANNING C D, et al. Extrapolation methods for accelerating PageRank computations[C]//Proceedings of the 12th International Conference on World Wide Web. New York: Association for Computing Machinery, 2003: 261-270. [3] BRIN S, PAGE L, MOTWANI R, et al. The PageRank citation ranking: bringing order to the web[R]. Stanford InfoLab, 1998. [4] 顾传青, 王磊. 一类修正的幂外推法加速PageRank计算[J]. 上海大学学报(自然科学版), 2013, 19(2): 150-153. (GU Chuanqing, WANG Lei. A class of modified power-extrapolation methods for speeding up PageRank computation[J]. Journal of Shanghai University (Natural Science) , 2013, 19(2): 150-153.(in Chinese) [5] GLEICH D F, GRAY A P, GREIF C, et al. An inner-outer iteration for computing PageRank[J]. SIAM Journal on Scientific Computing, 2010, 32(1): 349-371. doi: 10.1137/080727397 [6] GU C, XIE F, ZHANG K. A two-step matrix splitting iteration for computing PageRank[J]. Journal of Computational and Applied Mathematics, 2015, 278: 19-28. doi: 10.1016/j.cam.2014.09.022 [7] 潘春平. 关于PageRank的广义二级分裂迭代方法[J]. 计算数学, 2014, 36(4): 95-104. (PAN Chunping. On generalized two-stage iterative method for computing PageRank[J]. Mathematica Numerica Sinica, 2014, 36(4): 95-104.(in Chinese) [8] 陈星玎, 李思雨. 求解PageRank的多步幂法修正的广义二级分裂迭代法[J]. 数值计算与计算机应用, 2018, 39(4): 243-252. (CHEN Xingding, LI Siyu. A generalized two-step splitting iterative method modified with the multi-step power method for computing PageRank[J]. Journal on Numerical Methods and Computer Applications, 2018, 39(4): 243-252.(in Chinese) doi: 10.12288/szjs.2018.4.243 [9] GU C, WANG L. On the multi-splitting iteration method for computing PageRank[J]. Journal of Applied Mathematics and Computing, 2013, 42: 479-490. doi: 10.1007/s12190-013-0645-5 [10] 顾传青, 邵晨晨. 求解PageRank问题的GMRES-Inout方法[J]. 上海大学学报(自然科学版), 2017, 23(2): 179-184. (GU Chuanqing, SHAO Chenchen. A GMRES-Inout algorithm for computing PageRank problems[J]. Journal of Shanghai University (Natural Science) , 2017, 23(2): 179-184.(in Chinese) [11] 邱志红, 顾传青. 求解PageRank问题的GMRES重启的松弛两步分裂法[J]. 高等学校计算数学学报, 2018, 40(4): 331-345. (QIU Zhihong, GU Chuanqing. A GMRES-RPIO algorithm for computing PageRank problem[J]. Numerical Mathematics a Journal of Chinese Universities, 2018, 40(4): 331-345.(in Chinese) [12] 顾传青, 付友花, 王金波. 求解PageRank问题的Arnoldi松弛两步分裂算法[J]. 上海大学学报(自然科学版), 2019, 25(4): 484-492. (GU Chuanqing, FU Youhua, WANG Jinbo. Arnoldi-RPIO algorithm for computing PageRank problems[J]. Journal of Shanghai University (Natural Science) , 2019, 25(4): 484-492.(in Chinese) [13] SAAD Y, SCHULTZ M H. GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869. doi: 10.1137/0907058 [14] HAVELIWALA T H, KAMVAR S D. The second eigenvalue of the Google matrix[R]. Stanford: Stanford University, 2003. [15] LANGVILLE A N, MEYER C D. Deeper inside PageRank[J]. Internet Mathematics, 2004, 1(3): 335-380. doi: 10.1080/15427951.2004.10129091 [16] SAAD Y. Iterative Methods for Sparse Linear Systems[M]. 2nd ed. Society for Industrial and Applied Mathematics, 2003. -
计量
- 文章访问数: 685
- HTML全文浏览量: 344
- PDF下载量: 60
- 被引次数: 0
渝公网安备50010802005915号