A Complex Mode Method for Wind-Induced Responses of 6-Parameter Practical Viscoelastic Damping Energy Dissipation Structures Based on the Davenport Wind Speed Spectrum
-
摘要:
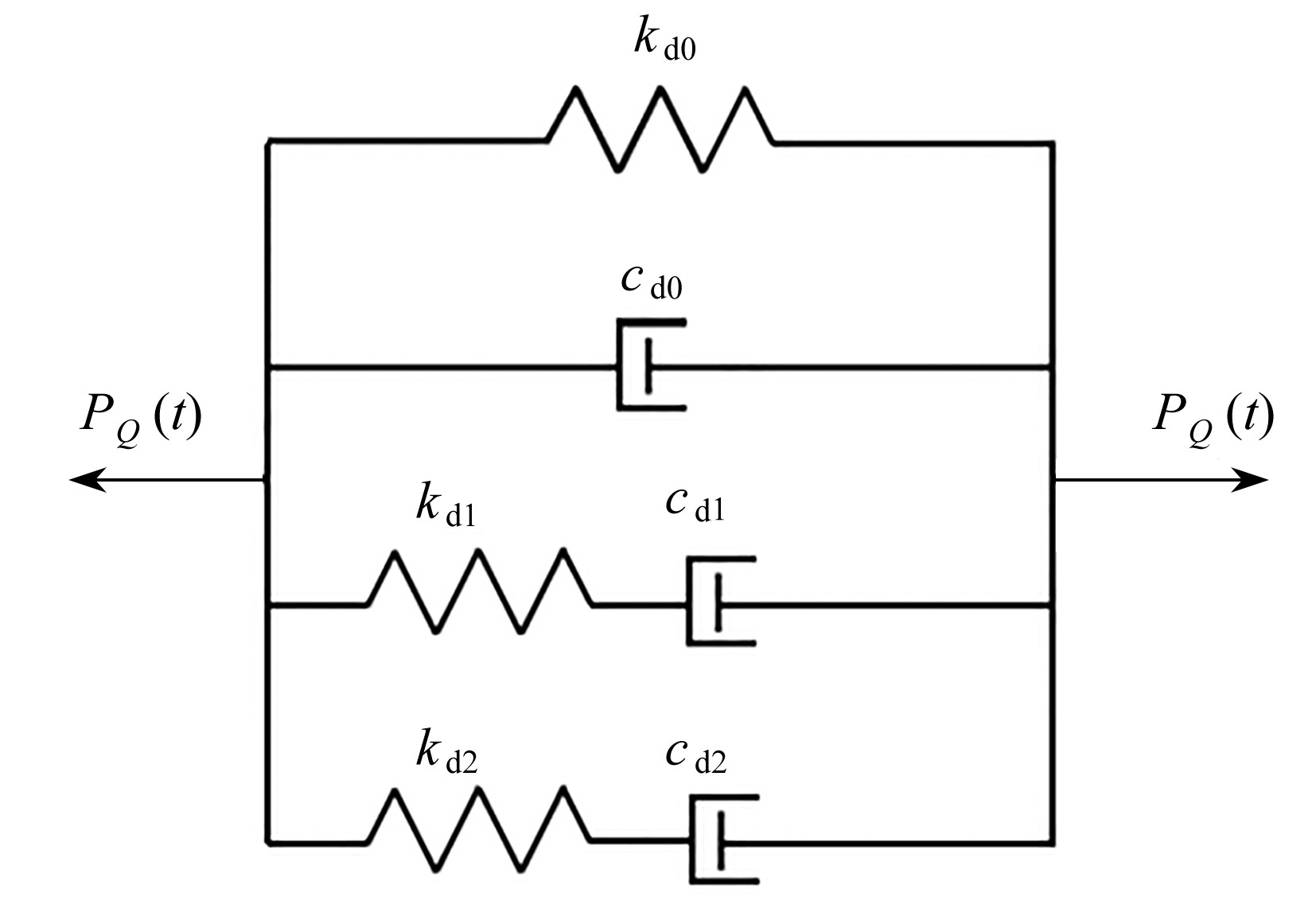
针对六参数实用黏弹性阻尼耗能结构，基于Davenport风速谱系列响应问题进行了系统的研究。首先，利用六参数黏弹性阻尼器的微分型本构关系，建立了耗能结构基于Davenport风速谱激励下的运动方程；然后，运用复模态法将耗能结构的运动方程由二阶微分方程转化为一阶方程，获得了耗能结构系统对风振激励响应的频域解和功率谱密度函数表达式；最后，利用数学恒等式，基于随机振动理论获得了耗能结构系统在Davenport风速谱激励下的响应和阻尼器受力的解析解。该文方法不仅考虑了结构系统在风振激励作用下全振型展开的结果，表达式较现有结果更为简便，效率及精度更高，且适用于非经典阻尼结构。
-
关键词:
- 六参数实用黏弹性阻尼耗能结构 /
- 复模态法 /
- Davenport风速谱 /
- 方差 /
- 阻尼器受力
Abstract:Based on the Davenport wind speed spectrum, the responses of 6-parameter practical viscoelastic damping energy dissipation structures were studied systematically. Firstly, the differential constitutive relation of the 6-parameter viscoelastic damper was used to establish the motion equation of the energy dissipation structure under the Davenport wind spectrum excitation. Then, the motion equation was transformed from the 2nd-order differential equation to the 1st-order one by means of the complex mode method, and the frequency-domain solution and the power spectral density function expression of the energy dissipation structure system under wind excitation were obtained. Finally, based on the random vibration theory, the analytical solutions of the response of the energy dissipation structure system under the Davenport wind spectrum excitation and the force response of the damper, were obtained with the mathematical identity. This method not only contains the results of the all-vibration-mode expansion of the structure system under wind excitation, but also has more simple and efficient expressions than existing methods, and applies to nonclassical structures.
-
图 2 六参数黏弹性阻尼耗能结构模型
Figure 2. The 6-parameter viscoelastic damping energy dissipation structure model
图 4 层间位移功率谱对比图
Figure 4. The comparison diagram of the interlayer displacement power spectrum
图 6 层间位移响应方差对比图
Figure 6. The comparison diagram of the interlayer displacement response variance
-
[1] 李英民, 赖明, 赵青, 等. 脉动风特性及其仿真研究[J]. 工程力学, 1993, 10(4): 117-124LI Yingmin, LAI Ming, ZHAO Qing, et al. Characteristics and simulation of fluctuating wind[J]. Engineering Mechanics, 1993, 10(4): 117-124.(in Chinese) [2] 许俊. 高层建筑顺风向等效静力风荷载研究[J]. 工程建设, 2020, 52(6): 20-25 doi: 10.13402/j.gcjs.2020.06.004XU Jun. Research on equivalent static wind load along the wind direction of high-rise buildings[J]. Engineering Construction, 2020, 52(6): 20-25.(in Chinese) doi: 10.13402/j.gcjs.2020.06.004 [3] DAVENPORT A G. The spectrum of horizontal gustiness near the ground in high winds[J]. Quarterly Journal of the Royal Meteorological Society, 1961, 87(372): 54-102. [4] 唐意, 顾明. 某超高层建筑TMD风振控制分析[J]. 振动与冲击, 2006, 25(2): 16-19 doi: 10.3969/j.issn.1000-3835.2006.02.004TANG Yi, GU Ming. Analysis of TMD wind induced vibration control of a super high rise building[J]. Journal of Vibration and Shock, 2006, 25(2): 16-19.(in Chinese) doi: 10.3969/j.issn.1000-3835.2006.02.004 [5] 李创第, 刘鹏, 葛新广, 等. 六参数实用粘弹性阻尼器单自由度减震系统非平稳响应分析[J]. 广西科技大学学报, 2018, 29(2): 110-118 doi: 10.16375/j.cnki.cn45-1395/t.2018.02.017LI chuangdi, LIU Peng, GE Xinguang, et al. Non stationary response analysis of single degree of freedom damping system with six-parameter practical viscoelastic damper[J]. Journal of Guangxi University of Science and Technology, 2018, 29(2): 110-118.(in Chinese) doi: 10.16375/j.cnki.cn45-1395/t.2018.02.017 [6] 魏春彤, 裴星洙. 附加黏弹性阻尼器的钢框架结构减震性能研究[J]. 振动与冲击, 2016, 35(20): 209-219 doi: 10.13465/j.cnki.jvs.2016.20.034WEI Chuntong, PEI Xingzhu. Study on seismic performance of steel frame structures with viscoelastic dampers[J]. Journal of Vibration and Shock, 2016, 35(20): 209-219.(in Chinese) doi: 10.13465/j.cnki.jvs.2016.20.034 [7] 李宏男. 结构振动控制实践的新进展[J]. 世界地震工程, 1995(2): 34-39LI Hongnan. New progress of structural vibration control practice[J]. World Seismological Engineering, 1995(2): 34-39.(in Chinese) [8] 钱华, 戴仁德, 郝洪伟. 半主动减振器控制算法仿真及实现[J]. 振动与冲击, 2013, 32(17): 104-108 doi: 10.3969/j.issn.1000-3835.2013.17.020QIAN Hua, DAI Rende, HAO Hongwei. Simulation and implementation of semi-active damper control algorithm[J]. Journal of Vibration and Shock, 2013, 32(17): 104-108.(in Chinese) doi: 10.3969/j.issn.1000-3835.2013.17.020 [9] 顾明, 陈更人, 伍杰明, 等. 用于斜拉桥抖振控制的多重调质阻尼器性能研究[J]. 振动与冲击, 1997, 16(1): 1-5 doi: 10.13465/j.cnki.jvs.1997.01.001GU Ming, CHEN Gengren, WU Jieming, et al. Study on performance of multiple tuned mass dampers for buffeting control of cable stayed bridges[J]. Journal of Vibration and Shock, 1997, 16(1): 1-5.(in Chinese) doi: 10.13465/j.cnki.jvs.1997.01.001 [10] MAZZA F, VULCANO A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers[J]. Earthquake Engineering and Structural Dynamics, 2011, 40(2): 155-174. doi: 10.1002/eqe.1012 [11] 吴巧云, 肖诗烨, 朱宏平. 连接Kelvin阻尼器的对称双塔楼结构被动控制研究[J]. 土木工程学报, 2018, 51(S1): 109-115 doi: 10.15951/j.tmgcxb.2018.s1.018WU Qiaoyun, XIAO Shiye, ZHU Hongping. Research on passive control of symmetrical double tower structure with Kelvin damper[J]. Chinese Journal of Civil Engineering, 2018, 51(S1): 109-115.(in Chinese) doi: 10.15951/j.tmgcxb.2018.s1.018 [12] 李创第, 陶欣欣, 尉霄腾. Maxwell阻尼耗能隔震结构平稳响应分析[J]. 广西大学学报(自然科学版), 2015, 40(4): 815-820 doi: 10.13624/j.cnki.issn.1001-7445.2015.0815LI Chuangdi, TAO Xinxin, WEI Xiaoteng. Stationary response analysis of Maxwell damping energy dissipation isolation structure[J]. Journal of Guangxi University (Natural Science Edition) , 2015, 40(4): 815-820.(in Chinese) doi: 10.13624/j.cnki.issn.1001-7445.2015.0815 [13] 李创第, 杜传知, 葛新广. 高层Maxwell耗能结构随机风振响应解析分析[J]. 广西科技大学学报, 2017, 28(2): 79-84 doi: 10.16375/j.cnki.cn45-1395/t.2017.02.013LI Chuangdi, DU Chuanzhi, GE Xinguang. Analytical analysis of random wind-induced response of high-rise Maxwell energy dissipation structure[J]. Journal of Guangxi University of Science and Technology, 2017, 28(2): 79-84.(in Chinese) doi: 10.16375/j.cnki.cn45-1395/t.2017.02.013 [14] 李创第, 葛新广, 朱倍权. 带五种被动减振器的高层建筑基于Davenport谱随机风振响应解析解法[J]. 工程力学, 2009, 26(4): 144-152LI Chuangdi, GE Xinguang, ZHU Beiquan. Analytical method for random wind-induced response of high-rise buildings with five kinds of passive dampers based on Davenport spectrum[J]. Engineering Mechanics, 2009, 26(4): 144-152.(in Chinese) [15] 李创第, 丁昊, 葛新广. 基于传递函数法的单自由粘弹性减震整体系统随机响应分析[J]. 广西科技大学学报, 2017, 28(3): 16-25LI Chuangdi, DING Hao, GE Xinguang. Random response analysis of single free viscoelastic damping system based on transfer function method[J]. Journal of Guangxi University of Science and Technology, 2017, 28(3): 16-25.(in Chinese) [16] 李永华, 李思明. 绝对位移直接求解的虚拟激励法[J]. 振动与冲击, 2009, 28(10): 185-190LI Yonghua, LI Siming. Virtual excitation method for direct solution of absolute displacement[J]. Journal of Vibration and Shock, 2009, 28(10): 185-190.(in Chinese) [17] 李创第, 王磊石, 邹万杰, 等. 广义Maxwell阻尼器高层结构随机风振响应解析法[J]. 广西大学学报(自然科学版), 2016, 41(4): 953-963LI Chuangdi, WANG Leishi, ZOU Wanjie, et al. Analytical method for random wind-induced response of high-rise structures with generalized Maxwell dampers[J]. Journal of Guangxi University (Natural Science Edition) , 2016, 41(4): 953-963.(in Chinese) [18] 周云, 刘纯, 汪大洋. 高层建筑楼顶钢塔风振效应的参数研究[J]. 振动与冲击, 2011, 30(2): 48-54 doi: 10.3969/j.issn.1000-3835.2011.02.010ZHOU Yun, LIU Chun, WANG Dayang. Parametric study on wind-induced vibration effect of steel tower on top of high-rise building[J]. Journal of Vibration and Shock, 2011, 30(2): 48-54.(in Chinese) doi: 10.3969/j.issn.1000-3835.2011.02.010 [19] 周岱, 马骏, 李华峰, 等. 大跨柔性空间结构风压和耦合风效应分析[J]. 振动与冲击, 2009, 28(6): 17-22 doi: 10.3969/j.issn.1000-3835.2009.06.005ZHOU Dai, MA Jun, LI Huafeng, et al. Analysis of wind pressure and coupling wind effect on long span flexible space structures[J]. Journal of Vibration and Shock, 2009, 28(6): 17-22.(in Chinese) doi: 10.3969/j.issn.1000-3835.2009.06.005 [20] 李桂青, 曹宏, 李秋胜, 等. 结构动力可靠性理论及其应用[M]. 北京: 地震出版社, 1993.LI Guiqing, CAO Hong, LI Qiusheng, et al. Structural Dynamic Reliability Theory and Its Application[M]. Beijing: Seismological Press, 1993. (in Chinese) [21] 葛新广, 张梦丹, 龚景海, 等. 频响函数二次正交法在Davenport风速谱下结构系列响应简明封闭解的应用研究[J]. 振动与冲击, 2021, 40(21): 207-214 doi: 10.13465/j.cnki.jvs.2021.21.028GE Xinguang, ZHANG Mengdan, GONG Jinghai, et al. Application of quadratic orthogonal method of frequency response function to concise closed solutions of structural series response under Davenport wind speed spectrum[J]. Journal of Vibration and Shock, 2021, 40(21): 207-214.(in Chinese) doi: 10.13465/j.cnki.jvs.2021.21.028 [22] 方同. 工程随机振动[M]. 北京: 国防工业出版社, 1995.FANG Tong. Engineering Random Vibration[M]. Beijing: National Defense Industry Press, 1995. (in Chinese) [23] DAVENPORT A G. The relationship of wind structure to wind loading[C]//Symposium on Wind Effect on Building and Structures. London, 1965: 54-102. [24] 林家浩, 张亚辉, 赵岩. 虚拟激励法在国内外工程界的应用回顾与展望[J]. 应用数学和力学, 2017, 38(1): 1-32 doi: 10.1007/s10483-016-2152-6LIN Jiahao, ZHANG Yahui, ZHAO Yan. Review and prospect of application of virtual excitation method in engineering field at home and abroad[J]. Applied Mathematics and Mechanics, 2017, 38(1): 1-32.(in Chinese) doi: 10.1007/s10483-016-2152-6 -
下载:
计量
- 文章访问数: 443
- HTML全文浏览量: 180
- PDF下载量: 44
- 被引次数: 0
渝公网安备50010802005915号