Topology Optimization of Heat Transfer Structures Under Gaussian Moving Heat Source Transient Effects
-
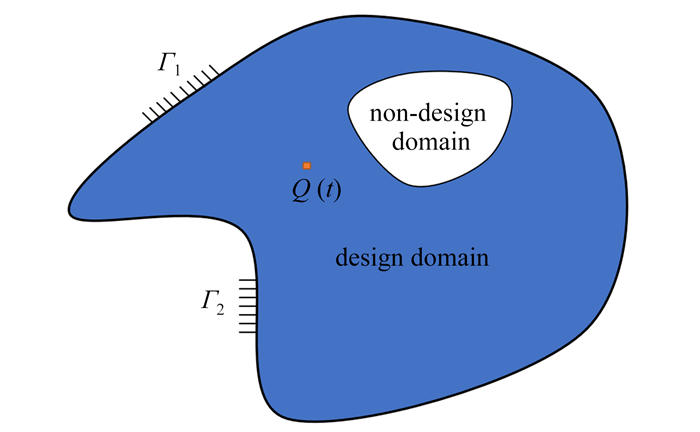
摘要: 针对热源位置随时间发生变化的结构热传导问题，考虑Gauss移动热源进行瞬态热传导拓扑优化设计. 分别以整个时间历程内传热结构散热弱度最小化与区域温度最大值最小化为设计目标，体积分数为约束条件，采用伴随变量法推导目标函数与约束条件的敏度信息，借助移动渐进线法更新设计变量，研究了不同Gauss热源移动路径与移动速度对拓扑优化结果的影响. 结果表明，瞬态拓扑结构相较于稳态结果具有明显时变性，同时最佳传热构型受到热源加热时间和移动速度及路径的多重影响.Abstract: For the structural heat transfer problem with heat sources moving with time, the Gaussian moving heat sources were considered for transient heat transfer topology optimization design. The design objectives are to minimize the total heat dissipation of the structure over the entire time history and to minimize the maximum temperature in particular regions, with the volume fraction as the constraint. Sensitivity information for the objectives and constraints was derived with the adjoint variable method, and design variables were updated with the moving asymptote method. The effects of different Gaussian heat source paths and speeds on the topology optimization results were studied. The numerical results indicate that, the transient topology structure exhibits pronounced time-varying characteristics compared to the steady-state results. Moreover, the optimal heat dissipation configuration depends on multiple factors, including the heating time, the path and the speed of the moving heat source.
-
图 3 Gauss热源热流密度及模拟路径
Figure 3. The Gaussian heat source heat flux density and the simulation path
图 4 Gaussian热源移动过程仿真
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.
Figure 4. Simulation of the Gaussian heat source movement process
图 6 稳态热传导与瞬态热传导的拓扑优化结果
Figure 6. Topologiy optimization results of steady-state and transient-state heat transfer
图 7 稳态热传导与移动热源不同速度的优化结果
Figure 7. Topologiy optimization results of steady-state heat conduction and moving heat source at different speeds
图 8 不同热源速度下的目标函数随迭代步数变化曲线
Figure 8. The objective function curves with the number of iteration steps
图 11 S形路径移动热源的拓扑构型
Figure 11. Topological configurations of the S-shaped path moving heat source
表 1 不同热源拓扑优化结果
Table 1. Results of different heat source topology optimizations
表 2 材料体积占比不同下拓扑优化结果
Table 2. Topology optimization results under different volume proportions of materials
表 3 Gauss移动热源不同移动范围的拓扑构型
Table 3. Topology optimization results of the Gaussian heat sources with different moving ranges
-
[1] CAROLINE P. Analysis of Heat and Mass Transfer[M]. Tritech Digital Media, 2018. [2] ATLURI S N, 匡震邦. 运动热源产生的温度场的有限元分析[J]. 应用数学和力学, 1986, 7(5): 383-400. http://www.applmathmech.cn/article/id/4002ATLURI S N, KUANG Zhenbang. A finite element analysis of temperature field generated by moving heat sources[J]. Applied Mathematics and Mechanics, 1986, 7(5): 383-400. (in Chinese) http://www.applmathmech.cn/article/id/4002 [3] 左孔天, 陈立平, 张云清, 等. 用拓扑优化方法进行热传导散热体的结构优化设计[J]. 机械工程学报, 2005, 41(4): 13-16.ZUO Kongtian, CHEN Liping, ZHANG Yunqing, et al. Structural optimal design of heat conductive body with topology optimization method[J]. Chinese Journal of Mechanical Engineering, 2005, 41(4): 13-16. (in Chinese) [4] BOUK T D. A review about the engineering design of optimal heat transfer systems using topology optimization[J]. Applied Thermal Engineering, 2017, 112: 841-854. doi: 10.1016/j.applthermaleng.2016.10.134 [5] 陈拥平, 高亮, 肖蜜. 基于变密度法的散热结构拓扑优化设计[J]. 计算机集成制造系统, 2018, 24(1): 117-126.CHEN Yongping, GAO Liang, XIAO Mi. Topology optimization design of heat dissipation structure based on density method[J]. Computer Integrated Manufacturing Systems, 2018, 24(1): 117-126. (in Chinese) [6] 赵清海, 张洪信, 蒋荣超, 等. 考虑拓扑相关热载荷的散热结构多相材料拓扑优化设计[J]. 中国机械工程, 2020, 31(20): 2403-2411.ZHAO Qinghai, ZHANG Hongxin, JIANG Rongchao, et al. Multi-phase material topology optimization design of heat dissipation structures considering topology-dependent heat sources[J]. China Mechanical Engineering, 2020, 31(20): 2403-2411. (in Chinese) [7] 张晖, 刘书田, 张雄. 拓扑相关热载荷作用下稳态热传导结构拓扑优化[J]. 中国机械工程, 2009, 20(11): 1339-1343.ZHANG Hui, LIU Shutian, ZHANG Xiong. Topology optimization of steady-state heat conduction problems with design-dependent heat loads[J]. China Mechanical Engineering, 2009, 20(11): 1339-1343. (in Chinese) [8] 龙凯, 左正兴. 稳态热传导下的连续体结构拓扑优化[J]. 中国机械工程, 2007, 18(24): 2939-2943.LONG Kai, ZUO Zhengxing. Topological optimization of continuum structure for heat conduction[J]. China Mechanical Engineering, 2007, 18(24): 2939-2943. (in Chinese) [9] 闫浩, 吴晓明. 基于ordered-EAMP模型的多材料传热结构拓扑优化[J]. 航空动力学报, 2021, 36(5): 1007-1021.YAN Hao, WU Xiaoming. Multi-material topology optimization for heat transfer structure based on ordered-EAMP model[J]. Journal of Aerospace Power, 2021, 36(5): 1007-1021. (in Chinese) [10] ZHAO Q H, FAN C M, WANG F J, et al. Topology optimization of steady-state heat conduction structures using meshless generalized finite difference method[J]. Journal of Engineering, 2020, 119(10): 13-24. [11] TURTELTAUB S. Optimal material properties for transient problems[J]. Structural and Multidisciplinary Optimization, 2001, 22(2): 157-166. doi: 10.1007/s001580100133 [12] 吴书豪, 张永存, 刘书田. 考虑瞬态效应的承载隔热多功能结构拓扑优化[J]. 计算力学学报, 2022, 39(2): 142-149.WU Shuhao, ZHANG Yongcun, LIU Shutian. Topology optimization for multi-functional structure with both load-bearing and thermal insulation capability considering transient effect[J]. Chinese Journal of Computational Mechanics, 2022, 39(2): 142-149. (in Chinese) [13] WU S H, ZHANG Y C, LIU S T. Transient thermal dissipation efficiency based method for topology optimization of transient heat conduction structures[J]. International Journal of Heat and Mass Transfer, 2021, 170: 121004. doi: 10.1016/j.ijheatmasstransfer.2021.121004 [14] 李信卿, 赵清海, 龙凯, 等. 考虑瞬态效应的周期性多材料传热结构拓扑优化[J]. 航空学报, 2022, 43(12): 425964.LI Xinqing, ZHAO Qinghai, LONG Kai, et al. Topology optimization of periodic multi-material heat conduction structures considering transient effects[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(12): 425964. (in Chinese) [15] ZHUANG C G, XIONG Z H. Temperature-constrained topology optimization of transient heat conduction problems[J]. Numerical Heat Transfer (Part B): Fundamentals, 2015, 68(4): 366-385. doi: 10.1080/10407790.2015.1033306 [16] ROSENTHAL D. Mathematical theory of heat distribution during welding and cutting[J]. Welding Journal, 1941, 20(S): 220. [17] 黄飞, 马永斌. 移动热源作用下基于分数阶应变的三维弹性体热-机响应[J]. 应用数学和力学, 2021, 42(4): 373-384. doi: 10.21656/1000-0887.400346HUANG Fei, MA Yongbin. Thermomechanical responses of 3D media under moving heat sources based on fractional-order strains[J]. Applied Mathematics and Mechanics, 2021, 42(4): 373-384. (in Chinese) doi: 10.21656/1000-0887.400346 [18] 周焕林, 严俊, 余波, 等. 识别含热源瞬态热传导问题的热扩散系数[J]. 应用数学和力学, 2018, 39(2): 160-169. doi: 10.21656/1000-0887.380199ZHOU Huanlin, YAN Jun, YU Bo, et al. Identification of thermal diffusion coefficients for transient heat conduction problems with heat sources[J]. Applied Mathematics and Mechanics, 2018, 39(2): 160-169. (in Chinese) doi: 10.21656/1000-0887.380199 [19] 昌俊康, 段宝岩. 连续体结构拓扑优化的一种改进变密度法及其应用[J]. 计算力学学报, 2009, 26(2): 188-192.CHANG Junkang, DUAN Baoyan. An improved variable density method and application for topology optimization of continuum structures[J]. Chinese Journal of Computational Mechanics, 2009, 26(2): 188-192. (in Chinese) [20] 乔赫廷, 张永存, 刘书田. 散热结构拓扑优化目标函数的讨论[J]. 中国机械工程, 2011, 22(9): 1112-1117.QIAO Heting, ZHANG Yongcun, LIU Shutian. Discussion of objective functions in heat conduction topology optimization[J]. China Mechanical Engineering, 2011, 22(9): 1112-1117. (in Chinese) [21] D'OSTUNI S, LEO P, CASALINO G. FEM simulation of dissimilar aluminum titanium fiber laser welding using 2D and 3D Gaussian heat sources[J]. Metals , 2017, 7(8): 307. doi: 10.3390/met7080307 [22] 黄河, 高佳徐, 任智彬, 等. 内三角管式快速蓄放热单元的肋片拓扑优化[J]. 应用数学和力学, 2022, 43(11): 1238-1248. doi: 10.21656/1000-0887.420198HUANG He, GAO Jiaxu, REN Zhibin, et al. Topology optimization of fins for rapid heat storage and release in triangular-inside tube units[J]. Applied Mathematics and Mechanics, 2022, 43(11): 1238-1248. (in Chinese) doi: 10.21656/1000-0887.420198 -
下载:
计量
- 文章访问数: 421
- HTML全文浏览量: 110
- PDF下载量: 71
- 被引次数: 0
渝公网安备50010802005915号