地震激励下等横截面无限水库频域和时域响应的FEM-SBFEM计算方法
doi: 10.21656/1000-0887.450138
An FEM-SBFEM Coupled Method for Infinite Reservoir Responses With Uniform Cross Sections Under Seismic Excitations in Frequency and Time Domains
-
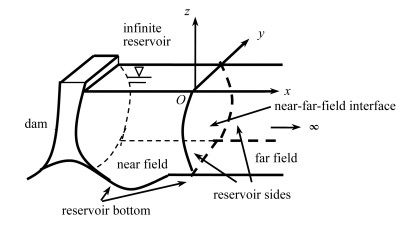
摘要: 坝体抗震设计和评估需要准确计算无限水库动力响应. 基于比例边界有限元法(scaled boundary finite element method，SBFEM)力学推导技术，推导了顺河向地震激励下等横截面无限水域频域响应计算公式，利用Fourier逆变换建立了时域响应控制方程，通过线性叠加推导了顺河、横河、竖直三向组合地震激励下的无限水域频域和时域响应的SBFEM计算公式. 结合有限元法，建立了无限水库频域和时域响应的FEM-SBFEM耦合方程. 分析了地震激励下的二维、三维等横截面无限水库频域、时域响应，数值验证了所建立计算公式的正确性. 所发展的FEM-SBFEM公式体系可推广应用于库底库岸具有吸收性的、横截面有任意几何形状的无限水库谐响应及瞬态响应分析.Abstract: It is necessary to accurately calculate the dynamic responses of infinite reservoirs in seismic design and evaluation of dams. Based on the mechanical derivation technique of the scaled boundary finite element method (SBFEM), the frequency domain response formulas for the infinite reservoirs with uniform cross sections under upstream seismic excitations were derived, and the time domain response governing equations were obtained through the inverse Fourier transform. Then the SBFEM formulas of frequency domain and time domain responses of infinite reservoirs under upstream, cross-stream and vertical seismic excitations were derived by linear superposition. The FEM-SBFEM coupled equations for frequency and time domain responses of infinite reservoirs were established. Based on these proposed formulations, the time domain and frequency domain responses of the 2D or 3D infinite reservoirs with uniform cross sections under seismic excitations were analyzed. The numerical results validate the accuracy of the proposed formulations. The proposed formulations can be used to analyze harmonic and transient responses of infinite reservoirs with arbitrary geometry and absorptive reservoir bottom under seismic excitations.
-
Key words:
- infinite reservoir /
- transient analysis /
- harmonic response analysis /
- SBFEM /
- FEM
edited-byedited-by1) 我刊编委肖世富来稿 -
图 5 顺河和竖直向激励下坝体z=0.6H处水动压力
Figure 5. Dam's pressures at z=0.6H induced by upstream and vertical excitations
图 6 半圆形等横截面无限水库
Figure 6. The semi-circular infinite reservoir with a uniform cross section
图 8 顺河向激励$a_{x} \mathrm{e}^{\mathrm{i} \omega t}$ 下$r=0.6 H, \theta=0$ 的压力
Figure 8. Pressures of point $r=0.6 H, \theta=0$ under upstream excitations $a_{x} \mathrm{e}^{\mathrm{i} \omega t}$
图 9 坚直向激励$a_{y} \mathrm{e}^{\mathrm{i} \omega t}$ 下$r=0.6 H, \theta=0$ 的压力
Figure 9. Pressures of point $r=0.6 H, \theta=0$ under vertical excitations $a_{y} \mathrm{e}^{\mathrm{i} \omega t}$
图 10 横河向激励$a_{z} \mathrm{e}^{\mathrm{i} \omega t}$ 下$r=0.6 H, \theta=45^{\circ}$ 的压力
Figure 10. Pressures of point $r=0.6 H, \theta=45^{\circ}$ under cross－stream excitations $a_{z} \mathrm{e}^{\mathrm{i} \omega t}$
图 12 顺河向激励$a_{x} \mathrm{e}^{\mathrm{i} \omega t}$ 下重力坝坝面压力分布
Figure 12. Pressure distributions along the gravity dam surface under upstream exciations $a_{x} \mathrm{e}^{\mathrm{i} \omega t}$
-
[1] BEHROOZI A M, VAGHEFI M. Application of coupled RBFDQ-FEM as a meshless method for time-domain analysis of dam-reservoir systems subjected to earthquake excitation[J]. Engineering Analysis With Boundary Elements, 2023, 153 : 160-171. doi: 10.1016/j.enganabound.2023.05.017 [2] YE J, ZHOU H, ZHOU X. Hydrodynamic pressure on lateral side of dam excited by harmonic seismic vibration: a novel formulation[J]. Soil Dynamics and Earthquake Engineering, 2023, 164 : 107626. doi: 10.1016/j.soildyn.2022.107626 [3] KHIAVI M P, FERDOUSI A, KHIAVI A M. A probabilistic model for evaluation of the dynamic behavior of a concrete gravity dam considering the fluid-structure interaction[J]. Advances in Civil Engineering, 2023, 2023 : 9927608. [4] YA S, EISENTRÄGER S, QU Y L, et al. Seismic analysis of post-tensioned concrete gravity dams using scaled boundary finite elements implemented as ABAQUS UEL[J]. Soil Dynamics and Earthquake Engineering, 2023, 164 : 107620. doi: 10.1016/j.soildyn.2022.107620 [5] 李艳朋, 林皋, 胡志强, 等. 基于声固耦合法的拱坝-库水-地基相互作用分析[J]. 哈尔滨工程大学学报, 2022, 43 (4): 451-457.LI Yanpeng, LIN Gao, HU Zhiqiang, et al. Arch dam-reservoir-foundation interaction analysis based on the acoustic-structure coupling method[J]. Journal of Harbin Engineering University, 2022, 43 (4): 451-457. (in Chinese) [6] WOLF J P, SONG C. Finite-Element Modeling of Unbounded Media[M]. New York, USA: Wiley, 1996. [7] LIN G, WANG Y, HU Z Q. An efficient approach for frequency-domain and time-domain hydrodynamic analysis of dam-reservoir systems[J]. Earthquake Engineering & Structural Dynamics, 2012, 41 (13): 1725-1749. [8] LI S M, LIANG H, LI A M. A semi-analytical solution for characteristics of a dam-reservoir system with absorptive reservoir bottom[J]. Journal of Hydrodynamics, 2008, 20 (6): 727-734. doi: 10.1016/S1001-6058(09)60008-1 [9] LI S M. Scaled boundary finite element method for semi-infinite reservoir with uniform cross section[J]. International Journal of Computational Methods, 2012, 9 (1): 1240006. doi: 10.1142/S0219876212400063 [10] 王毅, 胡志强, 郭维东. 考虑坝体柔性的重力坝坝面地震动水压力计算[J]. 水利水电科技进展, 2019, 39 (3): 38-43.WANG Yi, HU Zhiqiang, GUO Weidong. Calculation of earthquake-induced hydrodynamic pressure considering gravity dam flexibility[J]. Advances in Science and Technology of Water Resources, 2019, 39 (3): 38-43. (in Chinese) [11] 李上明. 基于比例边界有限元法的坝库瞬态耦合分析[J]. 华中科技大学学报(自然科学版), 2011, 39 (9): 108-111.LI Shangming. Dam-reservoir transient coupling analysis based on SBFEM[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39 (9): 108-111. (in Chinese) [12] 李上明. 基于比例边界有限元法动态刚度矩阵的坝库耦合分析方法[J]. 工程力学, 2013, 30 (2): 313-317.LI Shangming. Transient analysis method for dam-reservoir interaction based on dynamic stiffness of sbfem[J]. Engineering Mechanics, 2013, 30 (2): 313-317. (in Chinese) [13] 李上明, 吴连军. 基于连分式与有限元法的坝库耦合瞬态分析方法[J]. 工程力学, 2016, 33 (4): 9-16.LI Shangming, WU Lianjun. Dam-reservoir interaction transient-method based on continued fraction formulation and fem[J]. Engineering Mechanics, 2016, 33 (4): 9-16. (in Chinese) [14] WANG X, JIN F, PREMPRAMOTE S, et al. Time-domain analysis of gravity dam-reservoir interaction using high-order doubly asymptotic open boundary[J]. Computers & Structures, 2011, 89 (7/8): 668-680. [15] QU Y L, CHEN D H, LIU L, et al. A direct time-domain procedure for the seismic analysis of dam-foundation-reservoir systems using the scaled boundary finite element method[J]. Computers and Geotechnics, 2021, 138 : 104364. doi: 10.1016/j.compgeo.2021.104364 [16] 许贺, 邹德高, 孔宪京. 基于FEM-SBFEM的坝-库水动力耦合简化分析方法[J]. 工程力学, 2019, 36 (12): 37-43.XU He, ZOU Degao, KONG Xianjing. A simplified dam-reservoir dynamic coupling analysis method based on fem-sbfem[J]. Engineering Mechanics, 2019, 36 (12): 37-43. (in Chinese) [17] LI S M. Diagonalization procedure for scaled boundary finite element method in modeling semi-infinite reservoir with uniform cross-section[J]. International Journal for Numerical Methods in Engineering, 2009, 80 (5): 596-608. doi: 10.1002/nme.2647 [18] WEBER B. Rational Transmitting Boundaries for Time-Domain Analysis of Dam-Reservoir Interaction[M]. New York: Springer-Verlag, 1994. [19] TSAI C S. Semi-analytical solution for hydrodynamic pressures on dams with arbitrary upstream face considering water compressibility[J]. Computers & Structures, 1992, 42 (4): 497-502. -
下载:
计量
- 文章访问数: 65
- HTML全文浏览量: 16
- PDF下载量: 15
- 被引次数: 0
渝公网安备50010802005915号