An Axisymmetric Contact Problem of Piezoelectric Materials Based on the Couple Stress Theory
-
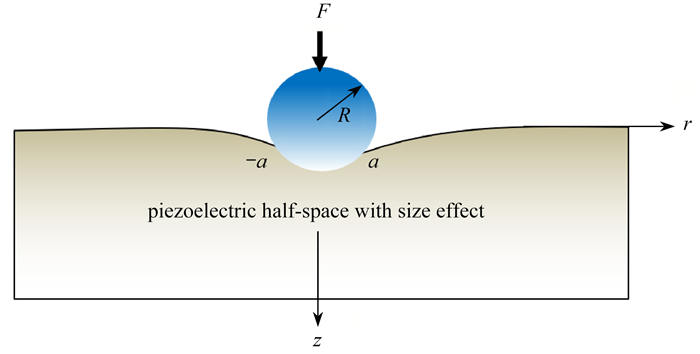
摘要: 基于偶应力理论，研究了刚性绝缘球压头与横观各向同性压电半空间尺度依赖的轴对称接触问题. 利用Hankel积分变换和积分最小二乘法，获得了接触压力. 讨论了特征材料长度对接触压力分布、接触半径和压痕深度的影响. 结果表明，基于偶应力理论获得的接触压力结果明显大于经典结果.Abstract: Based on the couple stress theory, the axisymmetric contact problem between a rigid insulating spherical punch and a transversely isotropic piezoelectric half-space was studied. With the Hankel integral transform and the integral least squares approach, the analytical solutions of the contact pressure were obtained. The effects of the characteristic material length on the contact pressure distribution, the contact radius and the indentation depth were discussed. The results indicate that, the contact pressure obtained based on the couple-stress theory is significantly greater than the classical results.
-
Key words:
- axisymmetric contact /
- piezoelectric material /
- size effect /
- couple stress theory
-
图 1 球压头与压电半空间尺度依赖的轴对称接触
Figure 1. Size-dependent axisymmetric contact between the spherical punch and the piezoelectric half-space
图 3 特征材料长度对接触压力分布的影响
Figure 3. The effects of the characteristic material length on the contact pressure distribution
图 4 法向加载F对最大接触压力的影响
Figure 4. The effects of normal loading F on the maximum contact pressure
图 6 特征材料长度对p(r)/pc(r)的影响
Figure 6. The effects of the characteristic material length on p(r)/pc(r)
图 7 特征材料长度对a/ac，p0/p0c，δ/δc的影响
Figure 7. The effects of the characteristic material length on a/ac, p0/p0c, δ/δc
C11/GPa C12/GPa C13/GPa C33/GPa C44/GPa e13/(C/m2) e33/(C/m2) e15/(C/m2) PZT-4 139 77.8 74.3 115 25.6 -5.2 15.1 12.7 BaTiO3 150 6.6 6.6 14.6 4.4 -17.3 17.5 11.4 ε11/(10－10·C/(V·m)) ε33/(10－10·C/(V·m)) f21/(10－11·Pa－1) PZT-4 64.61 56.2 1.772 8 BaTiO3 98.7 112 1.376 6 
下载: 导出CSV
表 2 接触半径a的收敛性分析
Table 2. Convergence analysis of contact radius a
M 2 3 4 a/μm 23.671 23.665 23.665
下载: 导出CSV
-
[1] STELMASHENKO N A, WALLS M G, BROWN L M, et al. Microindentations on W and Mo oriented single crystals: an STM study[J]. Acta Metallurgica et Materialia, 1993, 41(10): 2855-2865. doi: 10.1016/0956-7151(93)90100-7 [2] NIX W D, GAO H. Indentation size effects in crystalline materials: a law for strain gradient plasticity[J]. Journal of the Mechanics and Physics of Solids, 1998, 46(3): 411-425. doi: 10.1016/S0022-5096(97)00086-0 [3] MILLER R E, SHENOY V B. Size-dependent elastic properties of nanosized structural elements[J]. Nanotechnology, 2000, 11(3): 139-147. doi: 10.1088/0957-4484/11/3/301 [4] ZISIS T, GOURGIOTIS P A, BAXEVANAKIS K P, et al. Some basic contact problems in couple stress elasticity[J]. International Journal of Solids and Structures, 2014, 51(11/12): 2084-2095. [5] GOURGIOTIS P, ZISIS T. Two-dimensional indentation of microstructured solids characterized by couple-stress elasticity[J]. The Journal of Strain Analysis for Engineering Design, 2016, 51(4): 318-331. doi: 10.1177/0309324715611524 [6] ZISIS T. Anti-plane loading of microstructured materials in the context of couple stress theory of elasticity: half-planes and layers[J]. Archive of Applied Mechanics, 2018, 88(1): 97-110. [7] ZISIS T. Burmister's problem extended to a microstructuredlayer[J]. Journal of Mechanics of Materials and Structures, 2018, 13(2): 203-223. doi: 10.2140/jomms.2018.13.203 [8] GOURGIOTIS P A, ZISIS T, GIANNAKOPOULOS A E, et al. The Hertz contact problem in couple-stress elasticity[J]. International Journal of Solids and Structures, 2019, 168: 228-237. doi: 10.1016/j.ijsolstr.2019.03.032 [9] KARURIYA A N, BHANDAKKAR T K. Plane strain indentation on finite thickness bonded layer in couple stress elasticity[J]. International Journal of Solids and Structures, 2017, 108: 275-288. doi: 10.1016/j.ijsolstr.2016.12.027 [10] SONG H X, KE L L, WANG Y S. Sliding frictional contact analysis of an elastic solid with couple stresses[J]. International Journal of Mechanical Sciences, 2017, 133: 804-816. doi: 10.1016/j.ijmecsci.2017.09.037 [11] SONG H X, KE L, WANG Y, et al. Two-dimensional frictionless contact of a coated half-plane based on couple stress theory[J]. International Journal of Applied Mechanics, 2018, 10(5): 1850049. doi: 10.1142/S1758825118500497 [12] WANG Y, SHEN H, ZHANG X, et al. Semi-analytical study of microscopic two-dimensional partial slip contact problem within the framework of couple stress elasticity: cylindrical indenter[J]. International Journal of Solids and Structures, 2018, 138: 76-86. doi: 10.1016/j.ijsolstr.2017.12.030 [13] ÇÖMEZ I, EL-BORGI S. Sliding frictional contact problem of a layer indented by a rigid punch in couple stress elasticity[J]. Mathematics and Mechanics of Solids, 2023, 28(3): 730-747. doi: 10.1177/10812865221080551 [14] NABHANI M, EL KHLIFI M, GBEHE O S T, et al. Coupled couple stress and surface roughness effects on elasto-hydrodynamic contact[J]. Lubrication Science, 2014, 26(4): 251-271. doi: 10.1002/ls.1246 [15] WANG Y X, ZHANG X, SHEN H, et al. Three-dimensional contact analysis with couple stress elasticity[J]. International Journal of Mechanical Sciences, 2019, 153: 369-379. [16] WANG Y X, ZHANG X, SHEN H, et al. Couple stress-based 3D contact of elastic films[J]. International Journal of Solids and Structures, 2020, 191: 449-463. [17] LI P X, LIU T J. Axisymmetric adhesive contact of multi-layer couple-stress elastic structures involving graded nanostructured materials[J]. Applied Mathematical Modelling, 2022, 111: 501-520. doi: 10.1016/j.apm.2022.06.044 [18] ZHOU Y T, TIAN X J, DING S H. Microstructure size-dependent contact behavior of a thermoelectric film bonded to an elastic substrate with couple stress theory[J]. International Journal of Solids and Structures, 2022, 256: 111982. doi: 10.1016/j.ijsolstr.2022.111982 [19] LU R, LI M H, YANG Y, et al. Accurate extraction of large electromechanical coupling in piezoelectric MEMS resonators[J]. Journal of Microelectromechanical Systems, 2019, 28(2): 209-218. doi: 10.1109/JMEMS.2019.2892708 [20] WANG Z L, SONG J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays[J]. Science, 2006, 312(5771): 242-246. doi: 10.1126/science.1124005 [21] MIRZAEI A, LEE J H, MAJHI S M, et al. Resistive gas sensors based on metal-oxide nanowires[J]. Journal of Applied Physics, 2019, 126(24): 241102. doi: 10.1063/1.5118805 [22] SAHU S A, SINGHAL A, CHAUDHARY S. Surface wave propagation in functionally graded piezoelectric material: an analytical solution[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(3): 423-437. doi: 10.1177/1045389X17708047 [23] LI Y S, PAN E. Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory[J]. International Journal of Engineering Science, 2015, 97: 40-59. doi: 10.1016/j.ijengsci.2015.08.009 [24] RAZAVI H, BABADI A F, BENI Y T. Free vibration analysis of functionally graded piezoelectric cylindrical nanoshell based on consistent couple stress theory[J]. Composite Structures, 2017, 160: 1299-1309. doi: 10.1016/j.compstruct.2016.10.056 [25] WANG X, PAN E, FENG W J. Anti-plane Green's functions and cracks for piezoelectric material with couple stress and electric field gradient effects[J]. European Journal of Mechanics A: Solids, 2008, 27(3): 478-486. doi: 10.1016/j.euromechsol.2007.09.005 [26] SUN Y Y, SU J, SONG H X, et al. The size-dependent frictionless contact of piezoelectric materials[J]. International Journal of Mechanical Sciences, 2024, 261: 108685. doi: 10.1016/j.ijmecsci.2023.108685 [27] KE L L, YANG J, KITIPORNCHAI S, et al. Electro-mechanical frictionless contact behavior of a functionally graded piezoelectric layered half-plane under a rigid punch[J]. International Journal of Solids and Structures, 2008, 45(11/12): 3313-3333. [28] SU J, KE L L, WANG Y S. Axisymmetric frictionless contact of a functionally graded piezoelectric layered half-space under a conducting punch[J]. International Journal of Solids and Structures, 2016, 90: 45-59. doi: 10.1016/j.ijsolstr.2016.04.011 [29] CHEN W T, ENGEL P A. Impact and contact stress analysis in multilayer media[J]. International Journal of Solids and Structures, 1972, 8(11): 1257-1281. doi: 10.1016/0020-7683(72)90079-0 [30] O'SULLIVAN T C, KING R B. Sliding contact stress field due to a spherical indenter on a layered elastic half-space[J]. Journal of Tribology, 1988, 110(2): 235-240. doi: 10.1115/1.3261591 [31] LV X, KE L L, SU J, et al. Axisymmetric contact vibration analysis of a rigid spherical punch on a piezoelectric half-space[J]. International Journal of Solids and Structures, 2021, 210: 224-236. [32] WANG G F, YU S W, FENG X Q. A piezoelectric constitutive theory with rotation gradient effects[J]. European Journal of Mechanics A: Solids, 2004, 23(3): 455-466. doi: 10.1016/j.euromechsol.2003.12.005 [33] MINDLIN R D. Influence of couple-stresses on stress concentrations[J]. Experimental Mechanics, 1963, 3(1): 1-7. doi: 10.1007/BF02327219 [34] LIU C, YU J, ZHANG B, et al. Reflection and transmission of elastic waves in the multilayered orthotropic couple-stressed plates sandwiched between two elastic half-spaces[J]. Applied Mathematical Modelling, 2019, 75: 52-72. doi: 10.1016/j.apm.2019.05.023 -
图(7) / 表(2)
计量
- 文章访问数: 255
- HTML全文浏览量: 96
- PDF下载量: 55
- 被引次数: 0
渝公网安备50010802005915号