A Symplectic Approach for Buckling Analysis of Natural Fiber Reinforced Composite Shells Under Hygrothermal Aging
-
摘要:
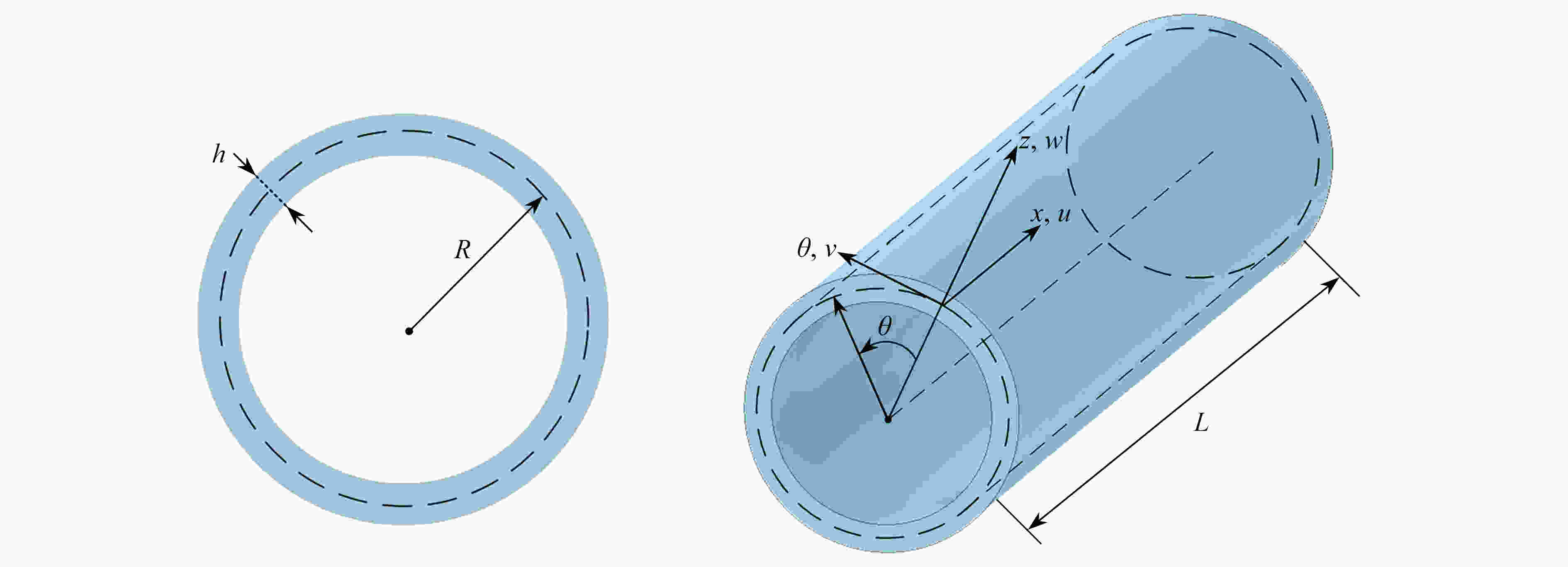
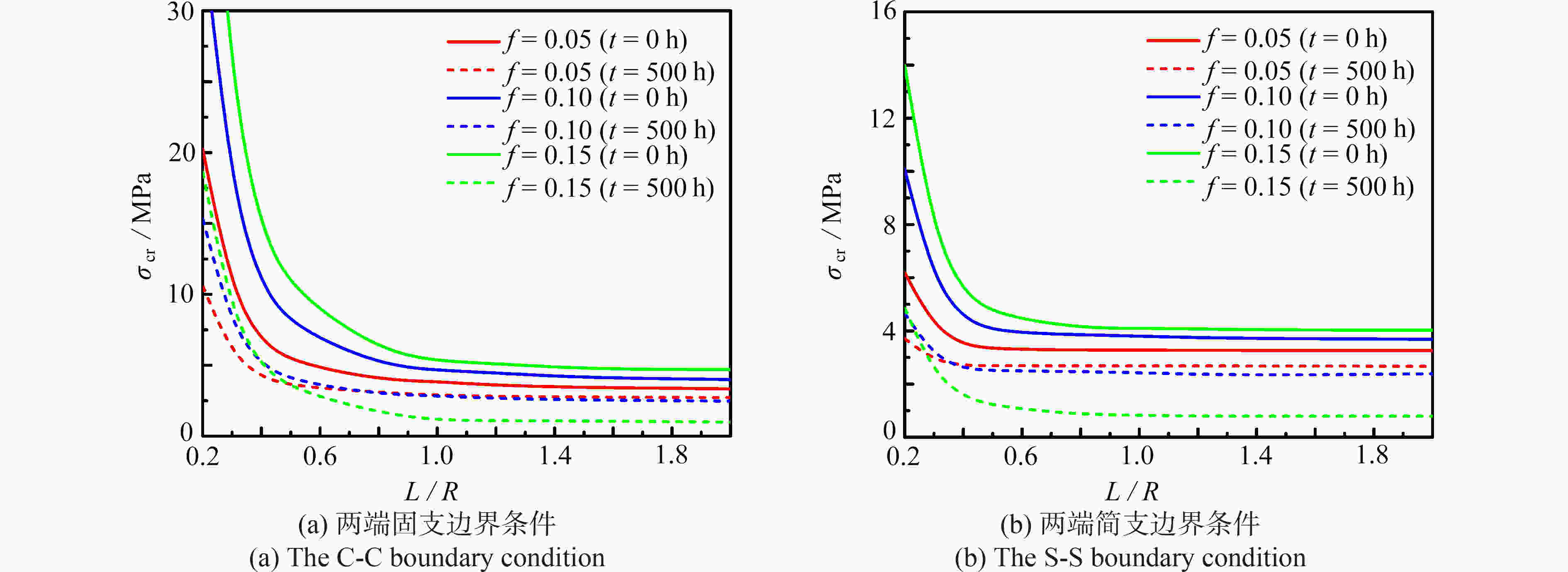
针对一类天然纤维增强复合(natural fiber reinforced composite, NFRC)圆柱壳的屈曲问题展开研究，基于Reissner壳体理论和辛方法，建立了轴压NFRC圆柱壳在Hamilton体系下的屈曲控制方程。将原问题归结为辛空间下的辛本征问题，通过求解辛本征值和本征解可以直接获得高精度的临界载荷和解析的屈曲模态。数值算例分析了NFRC材料的吸湿老化过程对辛本征解表达式的影响，并详细讨论了老化时间、纤维含量和几何参数对NFRC圆柱壳屈曲行为的影响。
Abstract:The buckling analysis of natural fiber reinforced (NFRC) cylindrical shells was performed based on Reissner’s shell theory and the symplectic approach. The governing buckling equations for axially-compressed NFRC cylindrical shells were established in the Hamiltonian system. Therefore, the original problem was reduced to a symplectic eigen-problem in the symplectic space. Accurate critical loads and analytical buckling mode shapes were directly obtained from the symplectic eigenvalues and eigensolutions. With numerical examples, the effects of hygroscopic aging on the expressions of eigensolutions were investigated. In addition, the influences of the aging time, the fiber content and the geometric parameters on the buckling behavior of NFRC cylindrical shells were discussed in detail.
-
图 2 不同纤维含量NFRC圆柱壳临界载荷随老化时间的变化曲线
Figure 2. Variations of critical loads for NFRC cylindrical shells with various f values vs. the aging time
图 3 纤维含量f = 0.15时NFRC圆柱壳屈曲模态图
Figure 3. Buckling mode shapes of NFRC cylindrical shells with f = 0.15
图 4 不同纤维含量NFRC圆柱壳临界载荷随壳体厚度变化曲线
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。
Figure 4. Variations of critical loads for NFRC cylindrical shells with various f values vs. the shell thickness
图 5 不同纤维含量NFRC圆柱壳临界载荷随壳体长度变化曲线
Figure 5. Variations of critical loads for NFRC cylindrical shells with various f values vs. the shell length
表 1 两端简支FGM圆柱壳的临界载荷(单位：MPa)
Table 1. Critical loads of an S-S FGM cylindrical shell (unit: MPa)
h / R 1/500 1/400 1/300 1/200 1/100 present 163.938 204.581 273.089 409.309 818.942 ref. [14] 164.148 205.185 273.580 410.371 820.741 
下载: 导出CSV
表 2 两端固支时NFRC圆柱壳的本征函数表达详解
Table 2. Detailed eigen function expressions of the C-C NFRC cylindrical shell
f t/h $ {{\boldsymbol{\xi}} } $ σcr/MPa case $ \pm {\lambda _{1,2}} $ $ \pm {\lambda _{3,4}} $ $ \pm {\lambda _{5,6}} $ $ \pm {\lambda _{7,8}} $ 0.05 0 iii 4.595i 4.249i 4.041−2.325i 4.041+2.325i 3.985 250 i 6.875i 6.505i 5.379 8.590 3.274 500 iii 6.264i 5.752i 4.733−4.109i 4.733+4.109i 3.155 0.10 0 i 4.525i 4.359i 1.770 11.45 4.374 250 i 5.898i 5.734i 2.818 12.28 3.031 500 iii 4.512i 4.274i 4.121−2.089i 4.121+2.089i 2.857 0.15 0 ii 10.39i 9.425i 0.835 1i 0.530 4i 4.850 250 i 3.717i 3.508i 1.038 12.83 1.232 500 i 2.976i 2.796i 0.7722 11.08 0.9117
下载: 导出CSV
表 3 两端简支时NFRC圆柱壳的本征函数表达详解
Table 3. Detailed eigen function expressions of the S-S NFRC cylindrical shell
f t/h $ {{\boldsymbol{\xi}} } $ σcr/MPa case $ \pm {\lambda _{1,2}} $ $ \pm {\lambda _{3,4}} $ $ \pm {\lambda _{5,6}} $ $ \pm {\lambda _{7,8}} $ 0.05 0 i 6.283i 4.212i 2.984 9.209 3.271 250 iii 6.283i 5.502i 5.011−3.477i 5.011+3.477i 2.763 500 iii 6.283i 5.735i 4.734−4.108i 4.734+4.108i 2.671 0.10 0 i 4.742i 3.142i 1.839 8.509 3.842 250 i 6.283i 4.214i 2.988 9.203 2.567 500 i 5.165i 5.035i 2.900 9.315 2.383 0.15 0 i 4.128i 3.975i 1.375 12.22 4.028 250 i 3.258i 3.040i 0.9613 10.63 1.056 500 i 3.386i 3.231i 0.8493 13.13 0.8091
下载: 导出CSV
-
[1] FARUK O, BLEDZKI A K, FINK H P, et al. Progress report on natural fiber reinforced composites[J]. Macromolecular Materials and Engineering, 2014, 299(1): 9-26. doi: 10.1002/mame.201300008 [2] 唐平, 曹红锦, 李佳蒙, 等. 天然植物纤维增强复合材料抗弹性研究[J]. 兵器装备工程学报, 2020, 41(8): 222-227. (TANG Ping, CAO Hongjing, LI Jiameng, et al. Study on eastic resistance of natural plant fiber reinforced composites[J]. Journal of Ordnance Equipment Engineering, 2020, 41(8): 222-227.(in Chinese) doi: 10.11809/bqzbgcxb2020.08.041 [3] WADDAR S, PITCHAIMANI J, DODDAMANI M, et al. Buckling and vibration behaviour of syntactic foam core sandwich beam with natural fiber composite facings under axial compressive loads[J]. Composites Part B: Engineering, 2019, 175: 107-133. [4] CHOW C, XING X, LI R. Moisture absorption studies of sisal fibre reinforced polypropylene composites[J]. Composites Science and Technology, 2007, 67(2): 306-313. doi: 10.1016/j.compscitech.2006.08.005 [5] FUQUA M A, HUO S, ULVEN C A. Natural fiber reinforced composites[J]. Polymer Reviews, 2012, 52(3): 259-320. doi: 10.1080/15583724.2012.705409 [6] 边佳燕, 刘钧, 鲍铮. 聚合物基复合材料吸湿研究进展[J]. 材料导报, 2016, 30(S2): 340-344. (BIAN Jiayan, LIU Jun, BAO Zheng. Research progress in moisture absorption of polymer matrix composites[J]. Materials Reports, 2016, 30(S2): 340-344.(in Chinese) [7] PAN Y, ZHONG Z. A nonlinear constitutive model of unidirectional natural fiber reinforced composites considering moisture absorption[J]. Journal of the Mechanics and Physics of Solids, 2014, 69: 132-142. doi: 10.1016/j.jmps.2014.04.007 [8] PAN Y, ZHONG Z. Modeling of the mechanical degradation induced by moisture absorption in short natural fiber reinforced composites[J]. Composites Science and Technology, 2014, 103: 22-27. doi: 10.1016/j.compscitech.2014.08.010 [9] WANG K F, WANG B L. A mechanical degradation model for bidirectional natural fiber reinforced composites under hydrothermal ageing and applying in buckling and vibration analysis[J]. Composite Structures, 2018, 206: 594-600. doi: 10.1016/j.compstruct.2018.08.063 [10] XU C, RONG D, ZHOU Z, et al. Vibration and buckling characteristics of cracked natural fiber reinforced composite plates with corner point-supports[J]. Engineering Structures, 2020, 214: 110614. doi: 10.1016/j.engstruct.2020.110614 [11] 姚伟岸, 钟万勰. 辛弹性力学[M]. 北京: 高等教育出版社, 2002.YAO Weian, ZHONG Wanxie. Symplectic Elasticity[M]. Beijing: Higher Education Press, 2002. （in Chinese） [12] NI Y, TONG Z, RONG D, et al. A new Hamiltonian-based approach for free vibration of a functionally graded orthotropic circular cylindrical shell embedded in an elastic medium[J]. Thin-Walled Structures, 2017, 120: 236-248. doi: 10.1016/j.tws.2017.09.003 [13] 周震寰, 李月杰, 范俊海, 等. 双功能梯度纳米梁系统振动分析的辛方法[J]. 应用数学和力学, 2018, 39(10): 1159-1171. (ZHOU Zhenhuan, LI Yuejie, FAN Junhai, et al. A symplectic approach for free vibration of functionally graded double-nanobeam systems emvedded in viscoelastic medium[J]. Applied Mathematics and Mechanics, 2018, 39(10): 1159-1171.(in Chinese) [14] HUANG H, HAN Q. Buckling of imperfect functionally graded cylindrical shells under axial compression[J]. European Journal of Mechanics A: Solids, 2008, 27(6): 1026-1036. doi: 10.1016/j.euromechsol.2008.01.004 -
计量
- 文章访问数: 1006
- HTML全文浏览量: 329
- PDF下载量: 60
- 被引次数: 0
渝公网安备50010802005915号