Nonlinear Numerical Simulation of Finite Elements Based on Fiber Beam Elements With Shear Effects for Structures
-
摘要:
基于Euler-Bernoulli梁理论的经典纤维模型忽略了剪切变形给截面带来的影响，为了得到更加精确的梁单元模型，该文基于考虑剪切效应的纤维梁单元，根据Timoshenko梁理论，推导了该纤维梁单元的刚度矩阵，并结合弹塑性增量理论，同时考虑了几何非线性和材料非线性的双重影响，建立了压弯剪复杂应力状态下结构非线性有限元分析理论。该文最后利用MATLAB编制了相关计算程序，对钢筋混凝土和矩形钢管混凝土的典型压弯剪构件进行有限元数值模拟，得到了构件的荷载-位移非线性全过程曲线。典型算例的验证结果表明：该文建立的非线性有限元分析理论是通用、可行和正确的。
Abstract:The classical fiber beam model based on the Euler-Bernoulli beam theory ignores the influence of shear deformation on the section. To get a more accurate beam element model, based on the fiber beam element with shear effects and the Timoshenko beam theory, the stiffness matrix of the fiber beam element was deduced, and the dual effects of geometric nonlinearity and material nonlinearity were considered at the same time, combined with the elastoplastic incremental theory. Then, the nonlinear finite element analysis theory for the structure under the complex stress state of compression, bending and shear was established. Finally, a program was coded on MATLAB to conduct finite element numerical simulation of the typical compression-bending-shear members of reinforced concrete and rectangular concrete-filled steel tube, and the nonlinear full-process load-displacement curves were obtained. The analysis of the numerical examples show that, the established nonlinear finite element analysis theory is universal, feasible and correct.
-
Key words:
- fiber beam element /
- structural nonlinearity /
- shear effect /
- finite element analysis
-
图 2 增量理论应力更新流程图
Figure 2. The flow chart for stress updating with the incremental theory
图 8 矩形钢管混凝土压弯剪试件计算模型
Figure 8. The calculation model for the rectangular CFST column under the compression-bending-shear loading condition
表 1 计算参数
Table 1. Calculation parameters
parameter value compressive strength of concrete $ f_{\rm{c}}^\prime = 32.1\;{\text{MPa}} $ Poisson’s ratio of concrete $ {\nu _{\rm{c}}} = 0.2 $ yield strength of rebar $ {f_{\rm{y}}} = 510\;{\text{MPa}} $ sectional shear coefficient $ {\kappa _y} = {\kappa _z} = 6/5 $ elastic modulus of concrete $ {E_{\rm{c}}} = 2.64 \times {10^4}\;{\text{MPa}} $ Poisson’s ratio of rebar $ {\nu _{\rm{s}}} = 0.3 $ elastic modulus of rebar $ {E_{\rm{s}}} = 2 \times {10^5}\;{\text{MPa}} $ peak compressive strain of the member $ \varepsilon {\text{ = }}0.005\;2 $ shear modulus of concrete $ {G_{\rm{c}}} = 1.1 \times {10^4}\;{\text{MPa}} $ moment of inertia $ I = 7.63 \times {10^{ - 3}}\;{{\text{m}}^4} $ shear modulus of rebar $ {G_{\rm{s}}} = 7.7 \times {10^4}\;{\text{MPa}} $ equivalent weight of the element $ P = 3\;539.25\;{\text{kN}} $ 
下载: 导出CSV
表 2 数值模拟结果
Table 2. Numerical simulation results
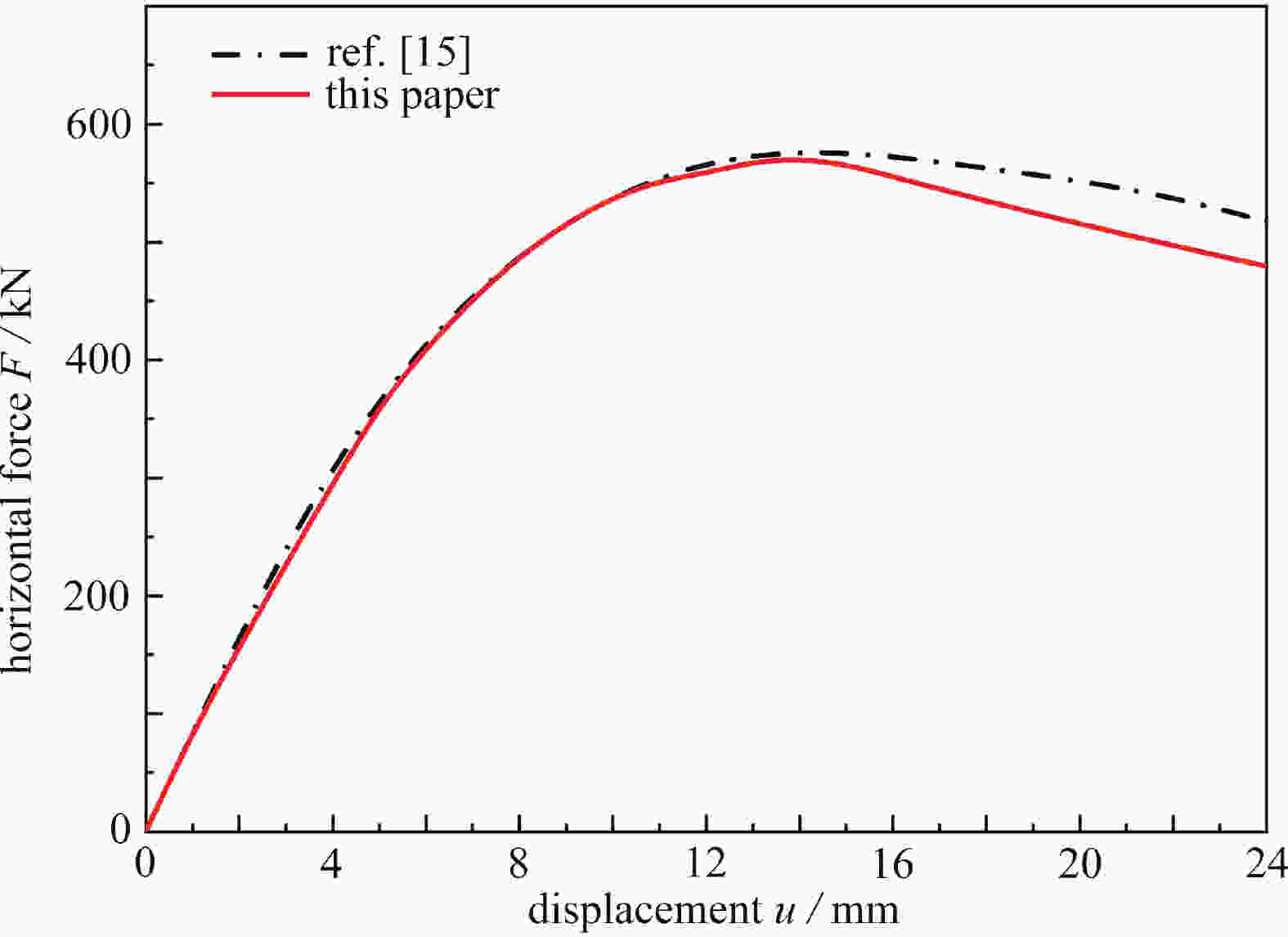
displacement u/mm ref. [15] FR/kN numerical simulation FN/kN error δ/% 2 167.16 156.02 6.66 4 313.14 294.85 5.84 6 417.97 409.75 1.97 8 490.91 487.48 0.70 10 540.35 537.67 0.50 12 568.83 558.61 1.80 14 577.99 570.97 1.22 16 573.22 555.43 3.10 18 562.80 534.98 4.94 20 552.04 515.57 6.61 22 538.23 497.12 7.64 24 517.62 479.59 7.35
下载: 导出CSV
-
[1] 马春来. 考虑剪切位移和多因素耦合影响下的空间梁非线性分析模型研究[D]. 硕士学位论文. 杭州: 浙江大学, 2008.MA Chunlai. Nonlinear analysis of space beam based on shear displacement and multi-factors coupling influence[D]. Master Thesis. Hangzhou: Zhejiang University, 2008. (in Chinese) [2] TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. Philosophical Magazine, 1921, 41(245): 744-746. [3] MARI A, SCORDELIS A. Nonlinear geometric material and time dependent analysis of three dimensional reinforced and prestressed concrete frames[R]. SESM Report. Department of Civil Engineering, University of California, 1984. [4] 胡郑州, 吴明儿. 考虑剪切效应三维纤维梁单元的几何非线性增量有限元分析[J]. 工程力学, 2014, 31(8): 134-143. (HU Zhengzhou, WU Ming’er. Geometrically nonlinear incremental finite element analysis of 3D fiber beam element considering shear effect[J]. Engineering Mechanics, 2014, 31(8): 134-143.(in Chinese) doi: 10.6052/j.issn.1000-4750.2013.03.0170 [5] 顾观东. 基于变形位移理论的空间梁柱非线性有限元分析模型研究[D]. 硕士学位论文. 杭州: 浙江大学, 2013.GU Guandong. Study on nonlinear spatial beam element model based on theory of deformation and displacement[D]. Master Thesis. Hangzhou: Zhejiang University, 2013.(in Chinese) [6] 郑欣怡. 考虑粘结滑移效应的新型钢筋混凝土纤维梁柱单元模型[D]. 硕士学位论文. 哈尔滨: 哈尔滨工业大学, 2019.ZHENG Xinyi. A new reinforced concrete fiber beam-column element model considering bond-slip effect[D]. Master Thesis. Harbin: Harbin Institute of Technology, 2019.(in Chinese) [7] THAI H T, KIM S E. Second-order inelastic analysis of cable-stayed bridges[J]. Finite Elements in Analysis & Design, 2012, 53(7): 48-55. [8] 张传超, 郑山锁, 李磊, 等. 基于柔度法的纤维梁柱单元及其参数分析[J]. 工业建筑, 2010, 40(12): 90-94. (ZHANG Chuanchao, ZHENG Shansuo, LI Lei, et al. Flexibility-based fiber beam-column element and its parametric analysis[J]. Industrial Construction, 2010, 40(12): 90-94.(in Chinese) [9] 马银. 基于纤维模型的型钢混凝土梁柱单元理论[D]. 硕士学位论文. 西安: 西安建筑科技大学, 2010.MA Yin. Element theory of steel reinforced concrete beam and column based on fiber model[D]. Master Thesis. Xi’an: Xi’an University of Architecture and Technology, 2010. (in Chinese) [10] 蔺鹏臻, 王富平, 柳兴成. 基于纤维梁模型的钢筋混凝土箱梁非线性分析[J]. 铁道建筑, 2019, 59(5): 22-26, 55. (LIN Pengzhen, WANG Fupin, LIU Xingcheng. Nonlinear analysis of RC box girder based on fiber beam model[J]. Railway Construction, 2019, 59(5): 22-26, 55.(in Chinese) doi: 10.3969/j.issn.1003-1995.2019.05.05 [11] KAGERMANOV A, CERESA P. 3D fiber-based frame element with multiaxial stress interaction for RC structures[J]. Advances in Civil Engineering, 2018, 2018: 8596970. [12] PARK K, KIM H, DAE J, et al. Generalized finite element formulation of fiber beam elements for distributed plasticity in multiple regions[J]. Computer-Aided Civil and Infrastructure Engineering, 2019, 34(2): 146-163. doi: 10.1111/mice.12389 [13] GENDY S S F M, AYOUB A. Explicit fiber beam-column elements for impact analysis of structures[J]. Journal of Structural Engineering, 2018, 144(7): 04018068. [14] BAZOUNE A, KHULIEF Y A, STEPHEN N G. Shape functions of three-dimensional Timoshenko beam element[J]. Journal of Sound and Vibration, 2003, 259(2): 473-480. doi: 10.1006/jsvi.2002.5122 [15] AL-AUKAILY A, SCOTT M H. Sensitivity analysis for displacement-controlled finite-element analyses[J]. Journal of Structural Engineering, 2018, 144(3): 04017222. doi: 10.1061/(ASCE)ST.1943-541X.0001983 [16] 杜修力, 曹惠, 金浏. 力-变位关系全过程模拟的有限元位移控制新方法[J]. 工程力学, 2012, 29(1): 1-6. (DU Xiuli, CAO Hui, JIN Liu. New finite element displacement control method for force-displacement relationship simulation in the whole process[J]. Engineering Mechanics, 2012, 29(1): 1-6.(in Chinese) [17] SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal, 1982, 79(1): 13-27. [18] KENT D C, PARK R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969-1990. [19] 王亚晋, 范重, 侯超, 等. 矩形钢管混凝土构件双向压弯剪受力性能研究[J]. 建筑结构学报, 2019, 40(S1): 257-263. (WANG Yajin, FAN Zhong, HOU Chao, et al. Research on the behavior of rectangular CFST members under bidirectional compression and bend sears[J]. Journal of Building Structures, 2019, 40(S1): 257-263.(in Chinese) [20] 韩林海. 钢管混凝土结构-理论与实践[M]. 北京: 科学出版社, 2004.HAN Linhai. Concrete-Filled Steel Tubular Structure-Theory and Practice[M]. Beijing: Science Press, 2004. (in Chinese) -
计量
- 文章访问数: 947
- HTML全文浏览量: 344
- PDF下载量: 97
- 被引次数: 0
渝公网安备50010802005915号