反平面塑性V形切口尖端应力和位移渐近解

李聪; 胡斌; 牛忠荣

doi:10.21656/1000-0887.420045

反平面塑性V形切口尖端应力和位移渐近解

doi: 10.21656/1000-0887.420045

1.
安徽建筑大学土木工程学院, 合肥 230601
2.
合肥工业大学土木与水利工程学院工程力学系, 合肥 230009

基金项目: 国家自然科学基金 (11272111)

详细信息

作者简介:
李聪(1989—), 女, 讲师, 博士(通讯作者. E-mail：Licong@ahjzu.edu.cn)

中图分类号: O344.3
计量
- 文章访问数: 779
- HTML全文浏览量: 292
- PDF下载量: 44
- 被引次数: 0
出版历程
- 收稿日期: 2021-02-20
- 录用日期: 2021-02-20
- 修回日期: 2021-05-27
- 网络出版日期: 2021-11-23
- 刊出日期: 2021-12-01

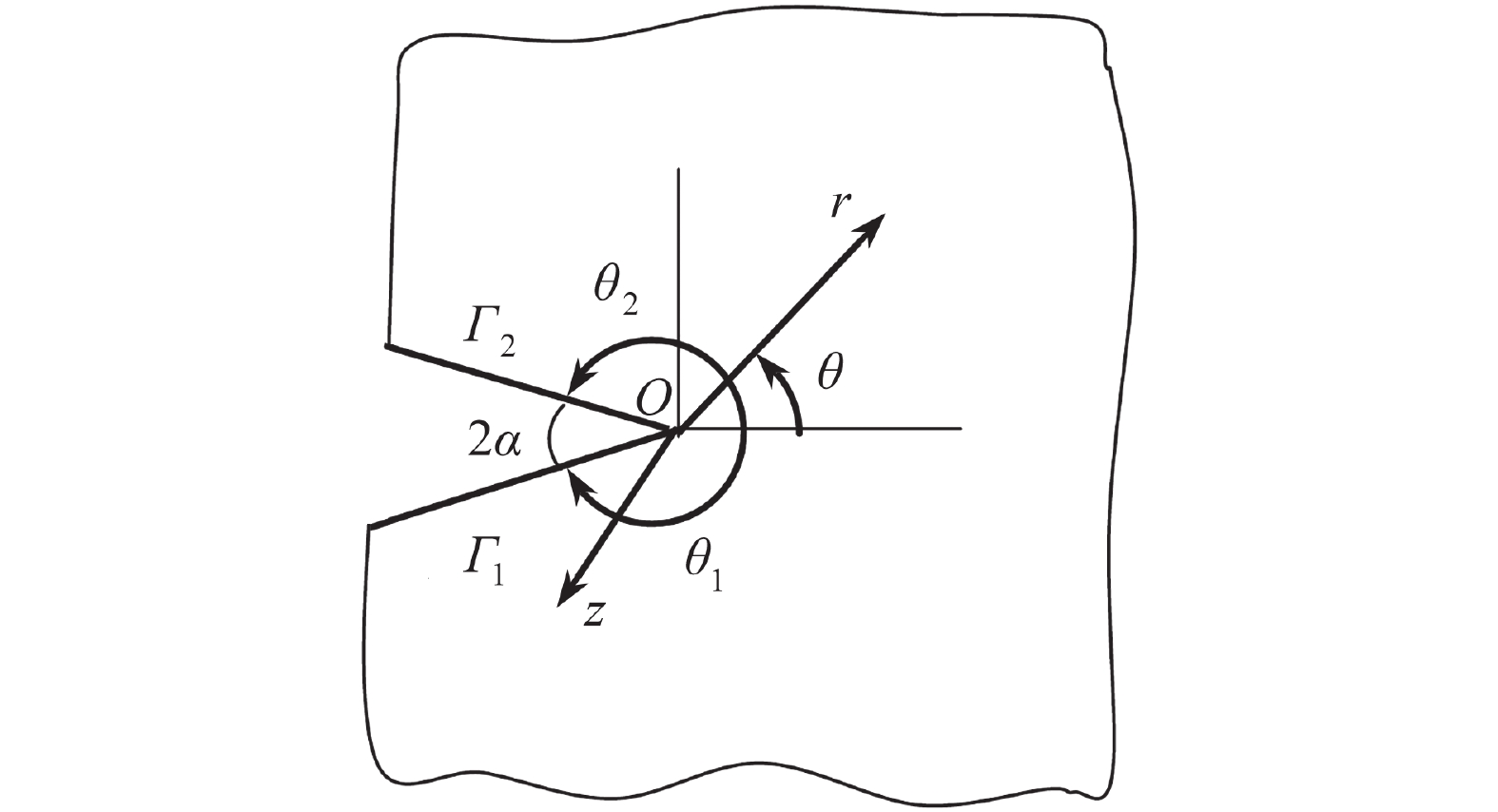
Asymptotic Solutions of Plastic Stress and Displacement at V-Notch Tips Under Anti-Plane Shear

1.
College of Civil Engineering, Anhui Jianzhu University, Hefei 230601, P.R.China
2.
Department of Engineering Mechanics, College of Civil Engineering, Hefei University of Technology, Hefei 230009, P.R.China

摘要

摘要:
提出了一种确定幂硬化材料反平面V形切口尖端应力和位移渐近解的主导项和高阶项的有效方法。首先通过在弹塑性理论基本方程中引入V形切口尖端应力场和位移场的渐近级数展开，建立以应力和位移为特征函数的非线性和线性常微分方程组。然后采用插值矩阵法求解常微分方程组，可得到多阶应力特征指数和其相对应的特征函数。该方法具有通用性强、精度高等优点，可处理任意开口角度和应变硬化指数的V形切口。典型算例验证了该方法的准确性和有效性。
- 弹塑性 /
- 反平面 /
- V形切口 /
- 渐近解 /
- 奇异性
Abstract:
An efficient method was developed to determine the first- and high-order terms of asymptotic solutions of plastic stress and displacement near V-notch tips under anti-plane shear in power-law hardening materials. Through introduction of the asymptotic series expansions of stress and displacement fields around the V-notch tip into the fundamental equations of the elastoplastic theory, the governing ordinary differential equations (ODEs) with the stress and displacement eigen-functions were established. Then the interpolating matrix method was employed to solve the resulting nonlinear and linear ODEs. Consequently, the high-order stress exponents and the associated eigen-solutions were obtained. The presented method, being capable of dealing with the V-notches with arbitrary opening angles and strain hardening indexes under anti-plane shear, has the advantages of great versatility and high accuracy. Typical examples were given to demonstrate the accuracy and effectiveness of this method.
- elastoplasticity /
- anti-plane /
- V-notch /
- asymptotic solution /
- singularity

HTML全文

图 1 反V形切口尖端区域

Figure 1. An anti-plane V-notch tip

下载: 全尺寸图片幻灯片

图 2 插值矩阵法迭代计算Ⅲ型裂纹第1阶应力指数$ {s_1} $收敛情况

Figure 2. First-order stress exponent s₁ in the iterative calculation of the mode Ⅲ crack with the interpolating matrix method

下载: 全尺寸图片幻灯片

图 3 幂硬化反平面Ⅲ型裂纹第1阶应力和位移特征角函数

Figure 3. The 1st-order stress and displacement eigen-functions for the mode Ⅲcrack

下载: 全尺寸图片幻灯片

图 4 幂硬化反平面Ⅲ型裂纹高阶应力和位移特征角函数，m=7

Figure 4. The high-order stress and displacement eigen-functions for the mode Ⅲ crack with m=7

下载: 全尺寸图片幻灯片

图 5 反平面切口第1阶应力特征角函数(m=7)

Figure 5. The 1st-order stress eigen-functions for the mode Ⅲ V-notch with m=7

下载: 全尺寸图片幻灯片

图 6 反平面切口第2阶应力特征角函数(m=7)

Figure 6. The 2nd-order stress eigen-functions for the mode Ⅲ V-notch with m=7

下载: 全尺寸图片幻灯片

图 7 反平面裂纹第1阶位移和应力特征角函数

Figure 7. The 1st-order stress and displacement eigen-functions for the mode Ⅲ V-notch

下载: 全尺寸图片幻灯片

图 8 反平面V形切口第1阶应力特征角函数(m=5)

Figure 8. The 1st-order stress and displacement eigen-functions for the mode Ⅲ V-notch (m=5)

下载: 全尺寸图片幻灯片

表 1 反平面Ⅲ型裂纹前4阶应力特征指数随硬化指数m的变化

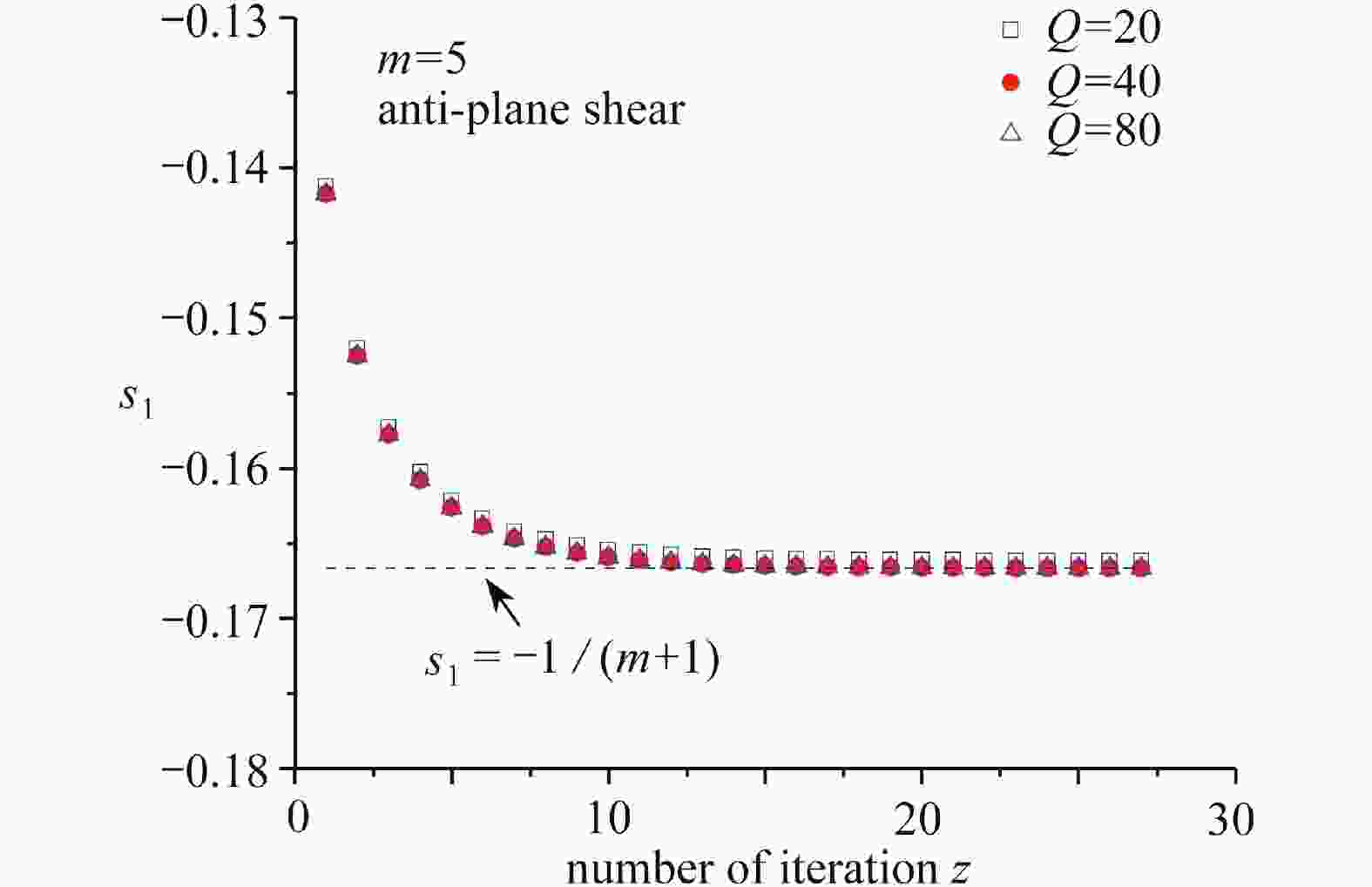
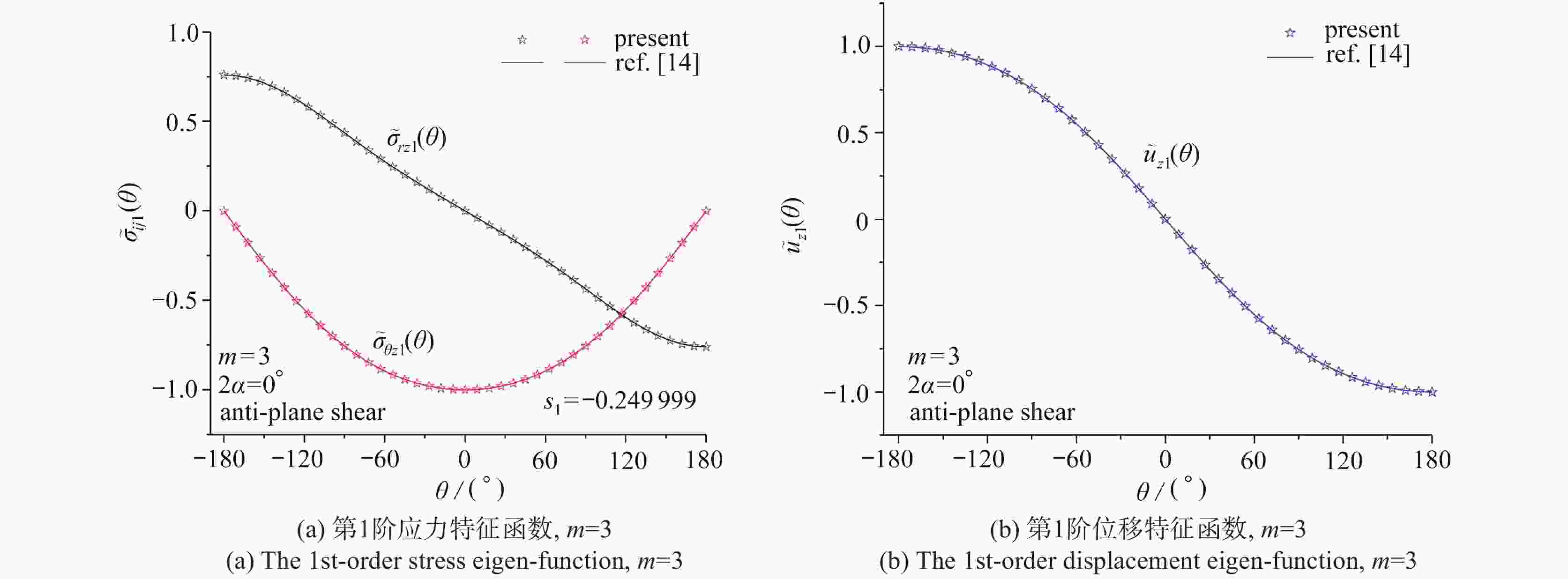
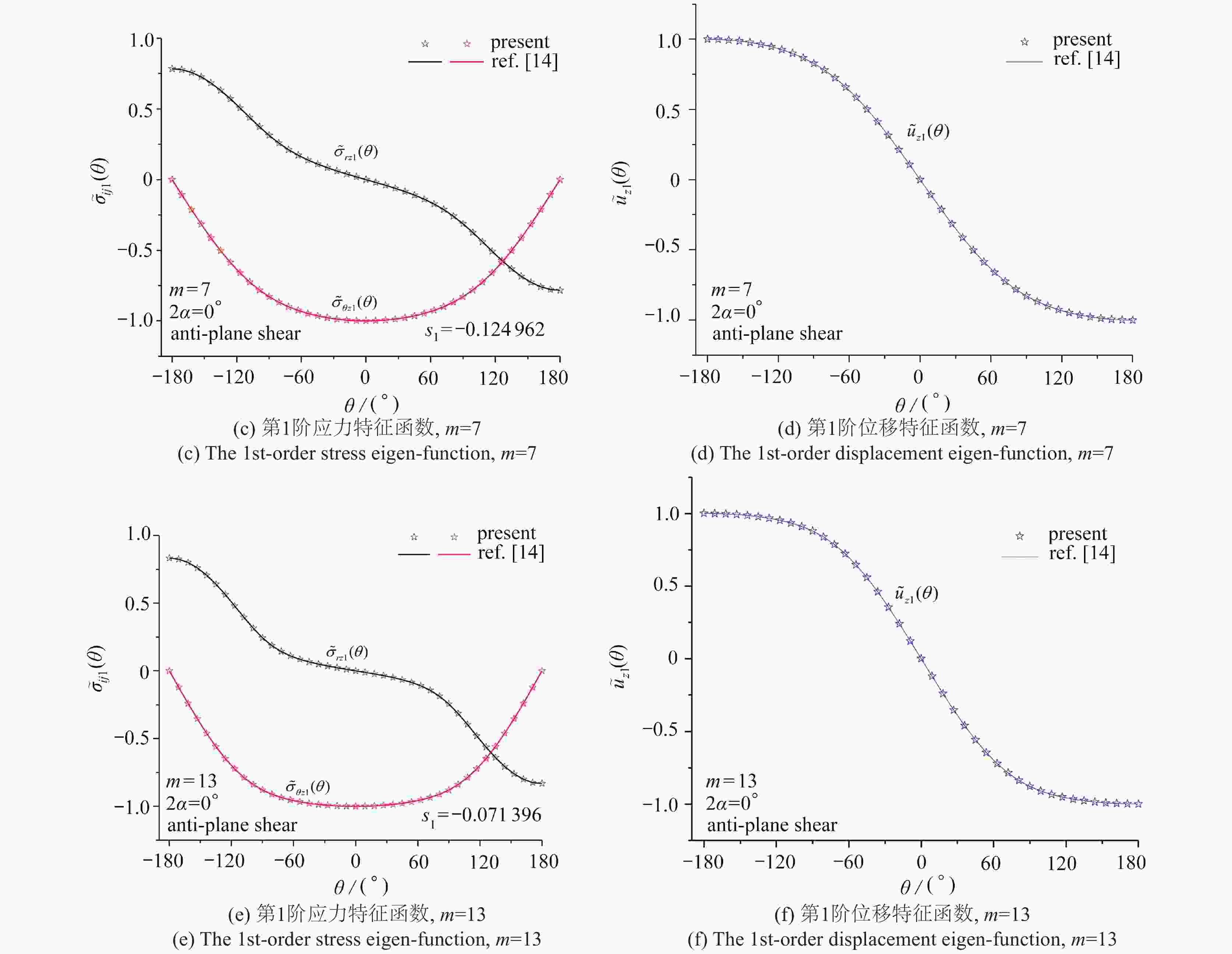
Table 1. Stress exponent $ {s_k} $ of the mode Ⅲ crack with various m values

$ {s_k} $	method	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	present (Q=20)	−0.249 999	−0.166 666	−0.124 999	−0.090 907	−0.071 426
	present (Q =40)	−0.249 999	−0.166 667	−0.125 000	−0.090 909	−0.071 429
	present (Q =80)	−0.249 999	−0.166 667	−0.125 000	−0.090 909	−0.071 429
	ref. [14]	−0.250 000	−0.166 667	−0.125 000	−0.090 909	−0.071 429
$ {s_{\text{2}}} $	present (Q =20)	0.249999^#	0.499998^#	0.437490	0.365759	0.314434
	present (Q =40)	0.249 999^#	0.500 001^#	0.435 761	0.363 758	0.312 255
	present (Q =80)	0.249 999^#	0.500 001^#	0.435 666	0.363 646	0.312 133
	ref. [14]	0.250 000^#	0.500 000^#	0.435 660	0.363 636	0.312 094
$ {s_{\text{3}}} $	present (Q =20)	0.574 150	0.501 559	0.624 995^#	0.727 256^#	0.700 294^×
	present (Q =40)	0.572 948	0.500 086	0.625 000^#	0.727 272^#	0.695 939^×
	present (Q =80)	0.572 879	0.500 004	0.625 000^#	0.727 272^#	0.695 695^×
	ref. [14]	0.572 876	0.500 000	0.625 000^#	0.727 273^#	0.695 617^×
$ {s_{\text{4}}} $	present (Q =20)	0.749 997^#	1.166 662^#	0.999 979^×	0.822 425^×	0.785 686^#
	present (Q =40)	0.749 997^#	1.166 669^#	0.996 522^×	0.818 425^×	0.785 719^#
	present (Q =80)	0.749 997^#	1.166 669^#	0.996 332^×	0.818 201^×	0.785 719^#
	ref. [14]	0.750 000^#	1.166 667^#	0.996 320^×	0.818 182^×	0.785 714^#

下载: 导出CSV

表 2 反平面V形切口($ {\text{2}}\alpha {\text{ = 3}}{{\text{0}}^ \circ } $)前4阶应力特征指数随硬化指数m的变化

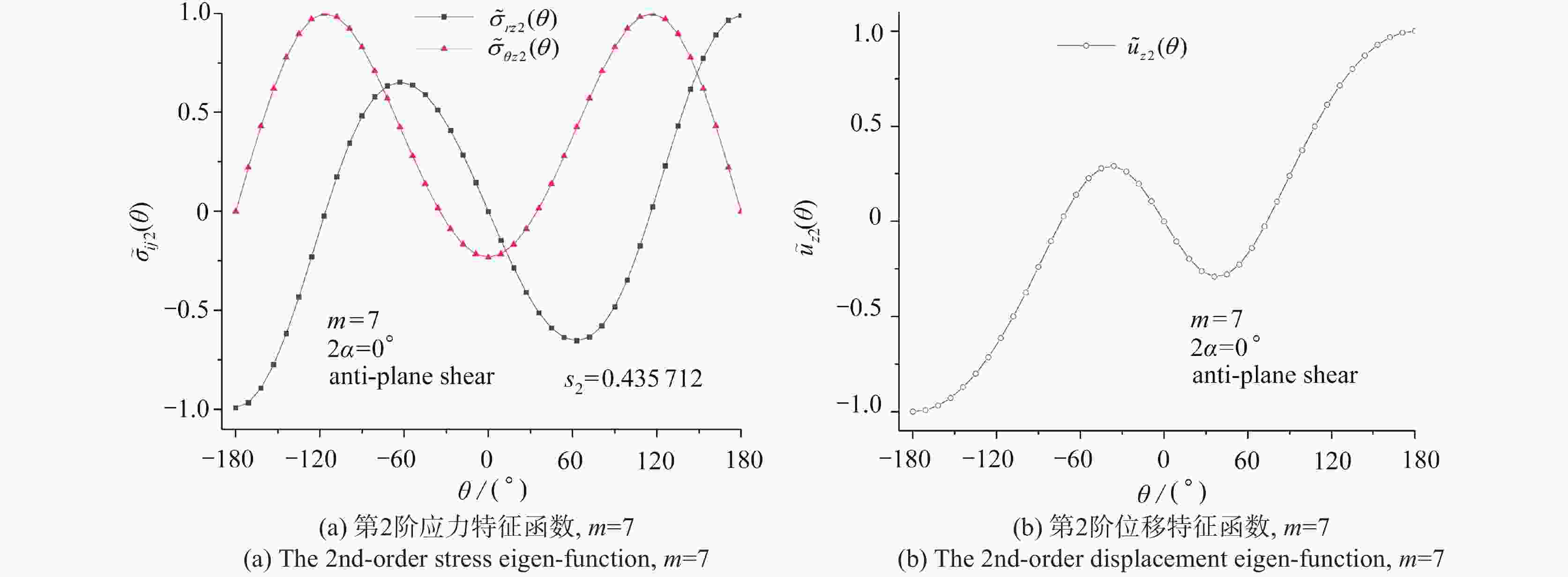
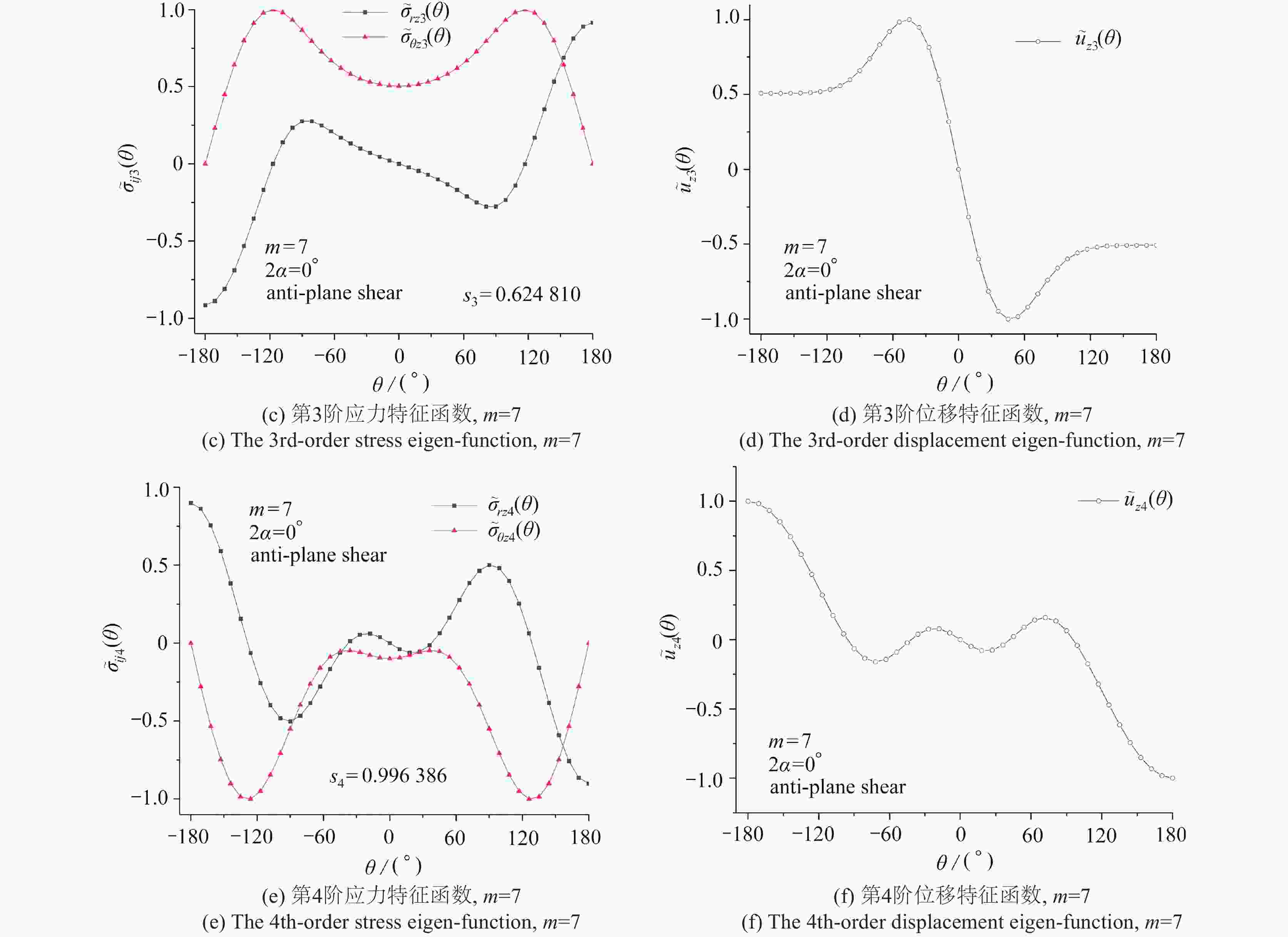
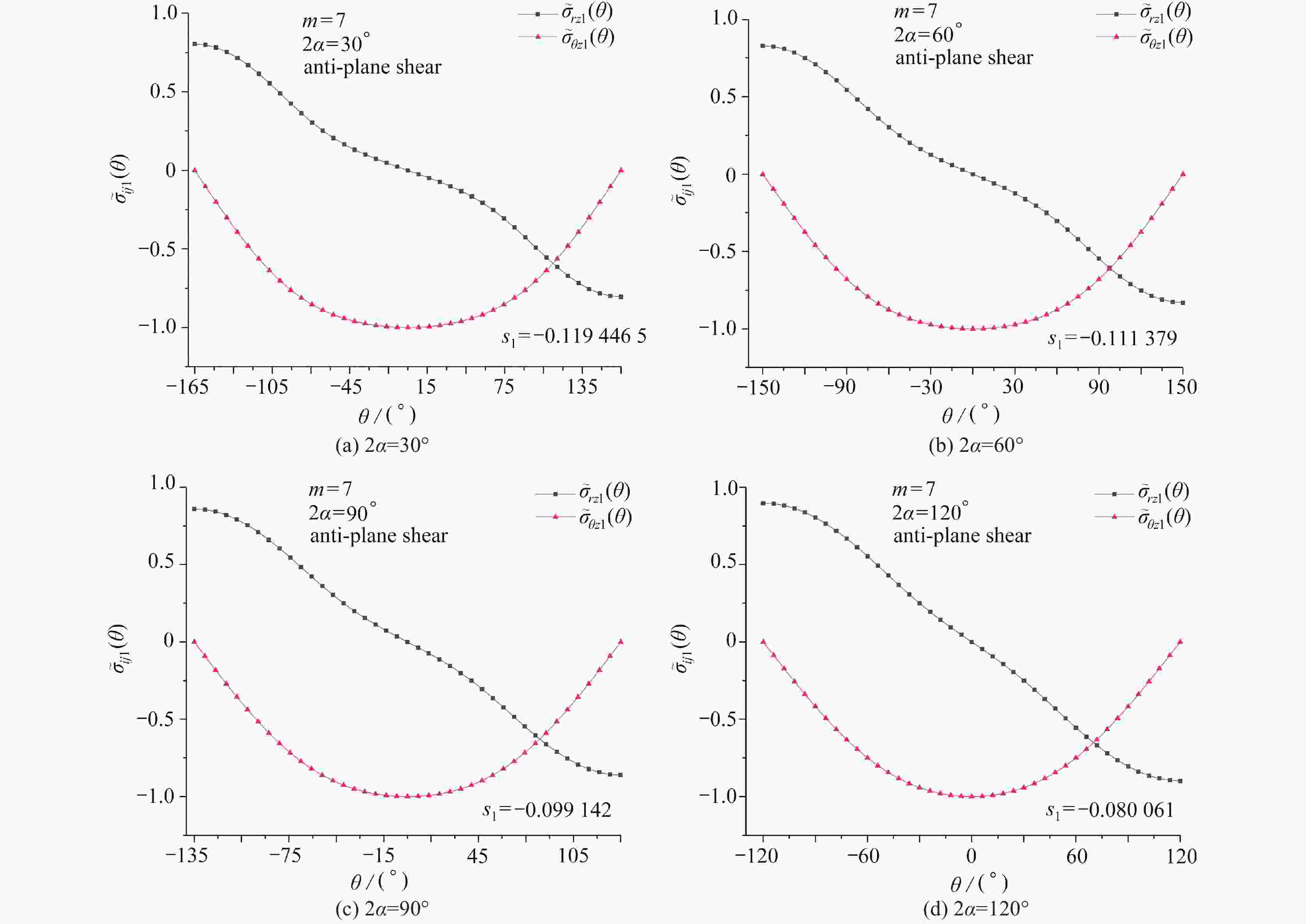
Table 2. Stress exponent $ {s_k} $ of the mode Ⅲ V-notch with $ {\text{2}}\alpha {\text{ = 3}}{{\text{0}}^ \circ } $ for various m values

$ {s_k} $	method	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	present(Q=20)	−0.232204	−0.157527	−0.119464	−0.087783	−0.069413
	present(Q=40)	−0.232206	−0.157527	−0.119465	−0.087784	−0.069415
	present(Q=80)	−0.232206	−0.157527	−0.119465	−0.087784	−0.069415
	ref. [17]	−0.232206	−0.157564	−0.119502	−0.087824	−0.069457
$ {s_{\text{2}}} $	present(Q=20)	0.232204^#	0.472581^#	0.554001	0.472991	0.413208
	present(Q=40)	0.232206^#	0.472581^#	0.551878	0.470411	0.410316
	present(Q=80)	0.232206^#	0.472581^#	0.551876	0.470409	0.410314
	ref. [17]	−	−	0.551851	0.470288	0.409963
$ {s_{\text{3}}} $	present(Q=20)	0.696612^×	0.623794	0.597320^#	0.702264^#	0.763543^#
	present(Q=40)	0.696618^×	0.621968	0.597325^#	0.702272^#	0.763565^#
	present(Q=80)	0.696618^×	0.621972	0.597325^#	0.702272^#	0.763565^#
	ref. [17]	−	0.622051	−	−	−
$ {s_{\text{4}}} $	present(Q=20)	0.700023	1.102689^#	1.227466^×	1.033765^×	0.895829^×
	present(Q=40)	0.698686	1.102689^#	1.223221^×	1.028606^×	0.890047^×
	present(Q=80)	0.698682	1.102689^#	1.223217^×	1.028602^×	0.890043^×
	ref. [17]	0.698604	−	−	−	−

下载: 导出CSV

表 3 反平面V形切口($ {\text{2}}\alpha {\text{ = 15}}{{\text{0}}^ \circ } $)前4阶应力特征指数随硬化指数m的变化

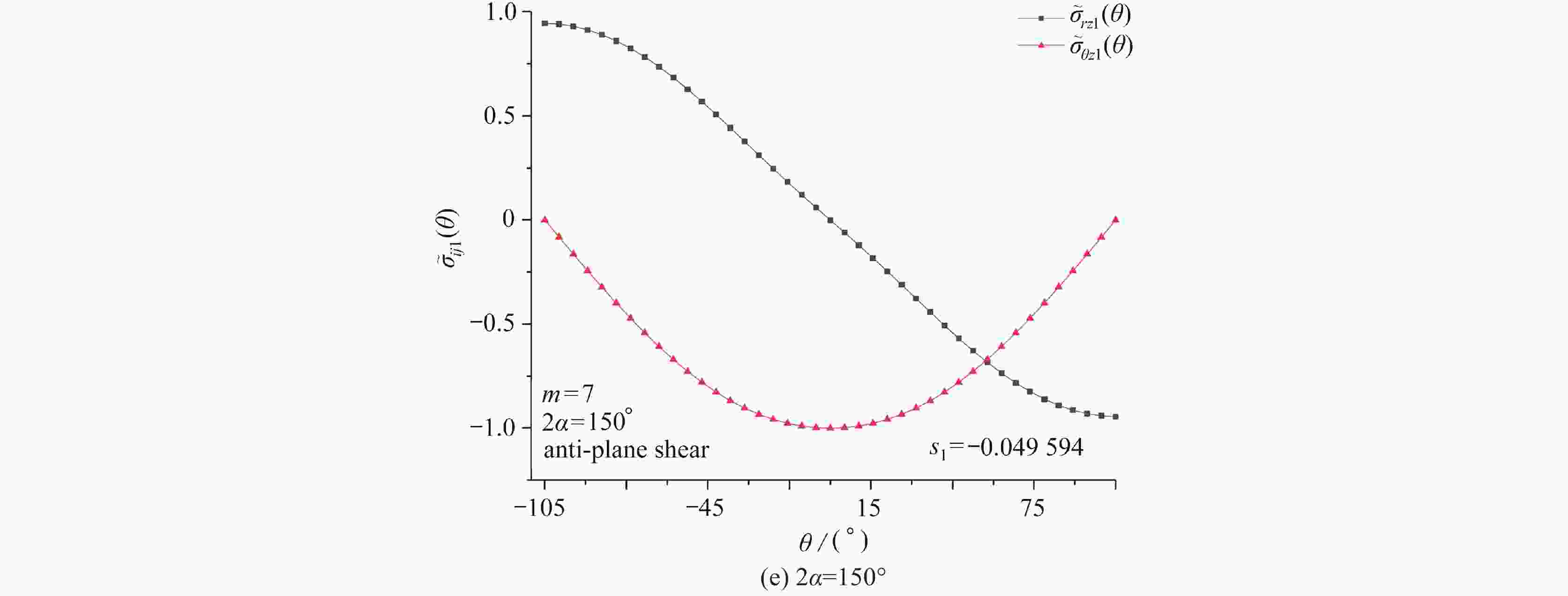
Table 3. Stress exponent $ {s_k} $ of the mode Ⅲ V-notch with $ {\text{2}}\alpha {\text{ = 15}}{{\text{0}}^ \circ } $ for various m values

$ {s_k} $	method	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	present(Q=20)	−0.080378	−0.060350	−0.049587	−0.039967	−0.033919
	present(Q=40)	−0.080383	−0.060356	−0.049564	−0.039974	−0.033925
	present(Q=80)	−0.080383	−0.060356	−0.049593	−0.039974	−0.033925
	ref. [17]	−0.080384	−0.060369	−0.049614	−0.040000	−0.033956
$ {s_{\text{2}}} $	present(Q=20)	0.080378^#	0.181051^#	0.247935^#	0.319736^#	0.373109^#`
	present(Q=40)	0.080383^#	0.181068^#	0.247970^#	0.319792^#	0.373175^#`
	present(Q=80)	0.080383^#	0.181068^#	0.247965^#	0.319792^#	0.373175^#`
	ref. [17]	−	−	−	−	−
$ {s_{\text{3}}} $	present(Q=20)	0.241134^#	0.422452^#	0.545457^#	0.679439^#	0.780137^#
	present(Q=40)	0.241149^#	0.422492^#	0.545534^#	0.679558^#	0.780275^#
	present(Q=80)	0.241149^#	0.422492^#	0.545523^#	0.679558^#	0.780275^#
	ref. [17]	−	−	−	−	−
$ {s_{\text{4}}} $	present(Q=20)	1.589836	1.556131	1.520007	1.470114	1.426214
	present(Q=40)	1.587821	1.553694	1.516597	1.464221	1.417315
	present(Q=80)	1.587820	1.553693	1.516597	1.464220	1.417314
	ref. [17]	1.587794	1.553562	1.516332	1.463944	1.416870

下载: 导出CSV

表 4 反平面V形切口($ {\text{2}}\alpha {\text{ = 6}}{{\text{0}}^ \circ } $)前4阶应力特征指数随硬化指数m的变化(Q=40)

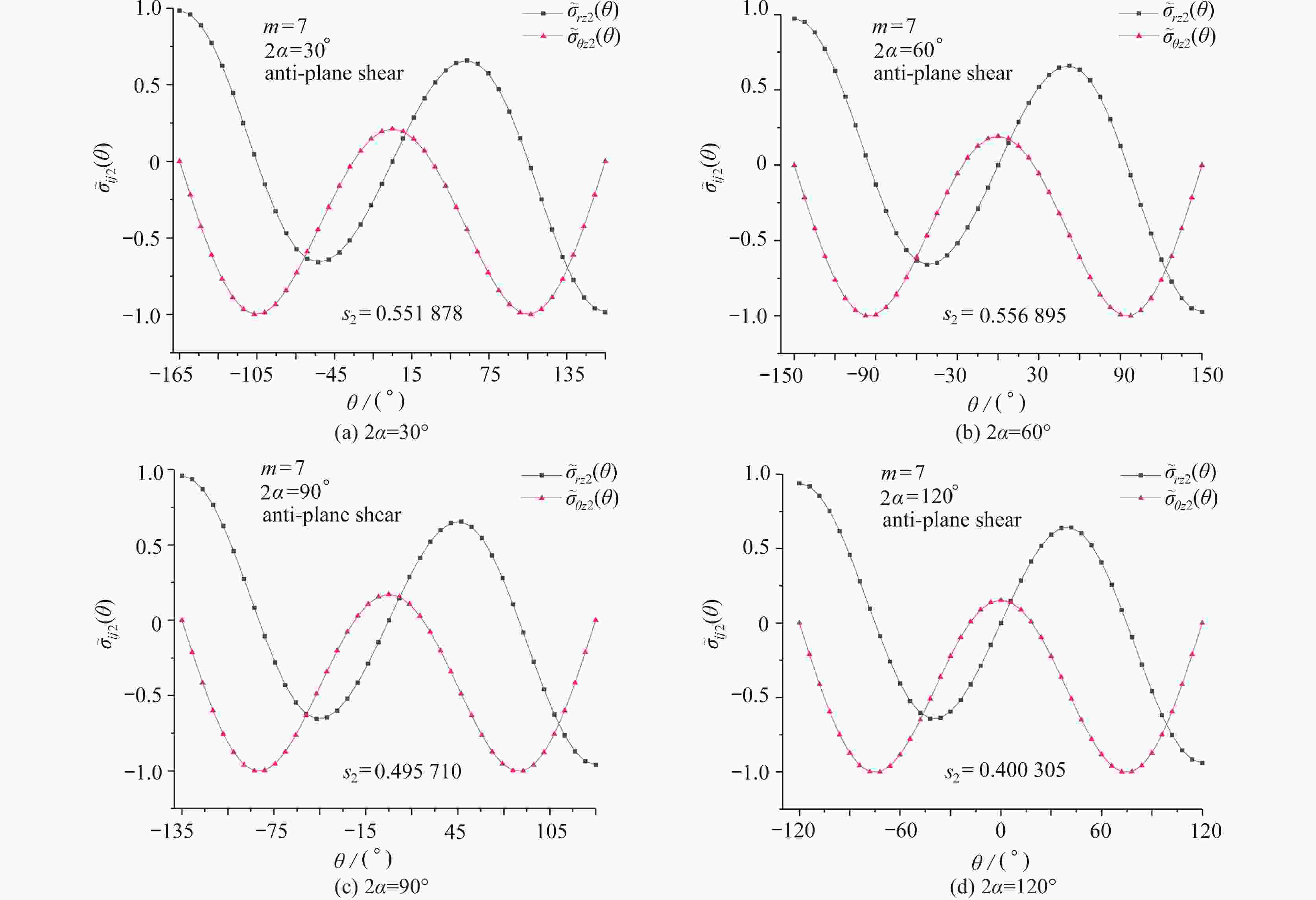
Table 4. Stress exponent $ {s_k} $ of the mode Ⅲ V-notch with $ {\text{2}}\alpha {\text{ = 6}}{{\text{0}}^ \circ } $ for various m values (Q=40)

$ {s_k} $	method	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	present	−0.209034	−0.144787	−0.111379	−0.083025	−0.066275
$ {s_{\text{1}}} $	ref. [17]	−0.209035	−0.144820	−0.111421	−0.083068	−0.066323
$ {s_{\text{2}}} $	present	0.209034^#	0.434361^#	0.556895^#	0.613636	0.545403
$ {s_{\text{2}}} $	ref. [17]	−	−	−	0.613578	0.545247
$ {s_{\text{3}}} $	present	0.627102^#	0.775407	0.702317	0.664200^#	0.729025^#
$ {s_{\text{3}}} $	ref. [17]	−	0.775369	0.702299	−	−
$ {s_{\text{4}}} $	present	0.851750	1.013509^#	1.225169^#	1.310297^×	1.157081^×
$ {s_{\text{4}}} $	ref. [17]	0.851659	−	−	−	−

下载: 导出CSV

表 5 反平面V形切口($ {\text{2}}\alpha {\text{ = 9}}{{\text{0}}^ \circ } $)前4阶应力特征指数随硬化指数m的变化(Q=40)

Table 5. Stress exponent $ {s_k} $ of the mode Ⅲ V-notch with $ {\text{2}}\alpha {\text{ = 9}}{{\text{0}}^ \circ } $ for various m values (Q=40)

$ {s_k} $	method	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	present	−0.178394	−0.126571	−0.099142	−0.075360	−0.060999
$ {s_{\text{1}}} $	ref. [17]	−0.178395	−0.126599	−0.099179	−0.075403	−0.061047
$ {s_{\text{2}}} $	present	0.178394^#	0.379713^#	0.495710^#	0.602880^#	0.670989^#
$ {s_{\text{2}}} $	ref. [17]	−	−	−	−	−
$ {s_{\text{3}}} $	present	0.535182^#	0.885997^#	0.899889	0.809746	0.736893
$ {s_{\text{3}}} $	ref. [17]	−	−	0.899826	0.809670	0.736783
$ {s_{\text{4}}} $	present	1.040992	0.970537	1.090562^#	1.281120^#	1.402977^#
$ {s_{\text{4}}} $	ref. [17]	1.040889	0.970465	−	−	−

下载: 导出CSV

表 6 反平面V形切口($ {\text{2}}\alpha {\text{ = 12}}{{\text{0}}^ \circ } $)前4阶应力特征指数随硬化指数m的变化(Q=40)

Table 6. Stress exponents $ {s_k} $ of the mode Ⅲ V-notch with $ {\text{2}}\alpha {\text{ = 12}}{{\text{0}}^ \circ } $ for various m values (Q=40)

$ {s_k} $	method	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	present	−0.137145	−0.099974	−0.080061	−0.060462	−0.051585
$ {s_{\text{1}}} $	ref. [17]	−0.137146	−0.100000	−0.080094	−0.062500	−0.051628
$ {s_{\text{2}}} $	present	0.137145^#	0.299922^#	0.400305^#	0.483696^#	0.567435^#
$ {s_{\text{2}}} $	ref. [17]	−	−	−	−	−
$ {s_{\text{3}}} $	present	0.411435^#	0.699818^#	0.880671^#	1.027854^#	1.013736
$ {s_{\text{3}}} $	ref. [17]	−	−	−	−	1.013494
$ {s_{\text{4}}} $	present	1.279549	1.222471	1.162660	1.082304	1.186455^#
$ {s_{\text{4}}} $	ref. [17]	1.279434	1.222375	1.162546	1.082129	−

下载: 导出CSV

表 7 反平面V形切口前4阶应力特征指数随硬化指数m和张角2α的变化 ( Q =40)

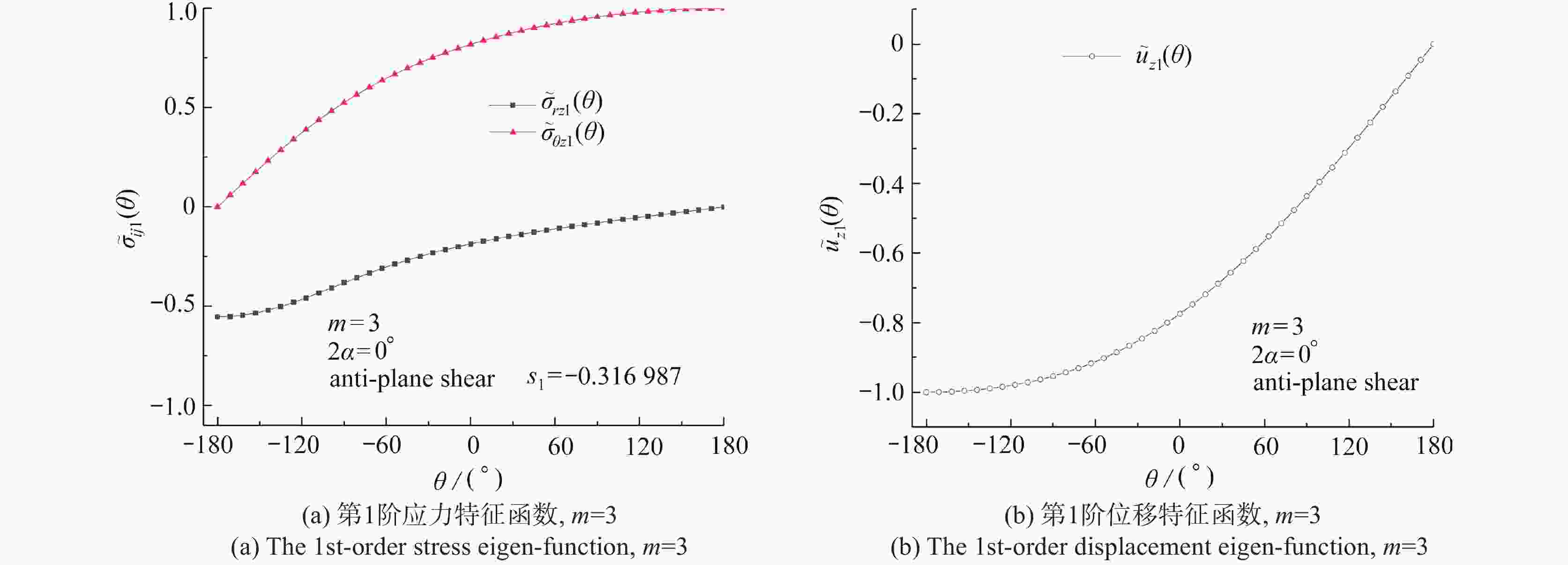
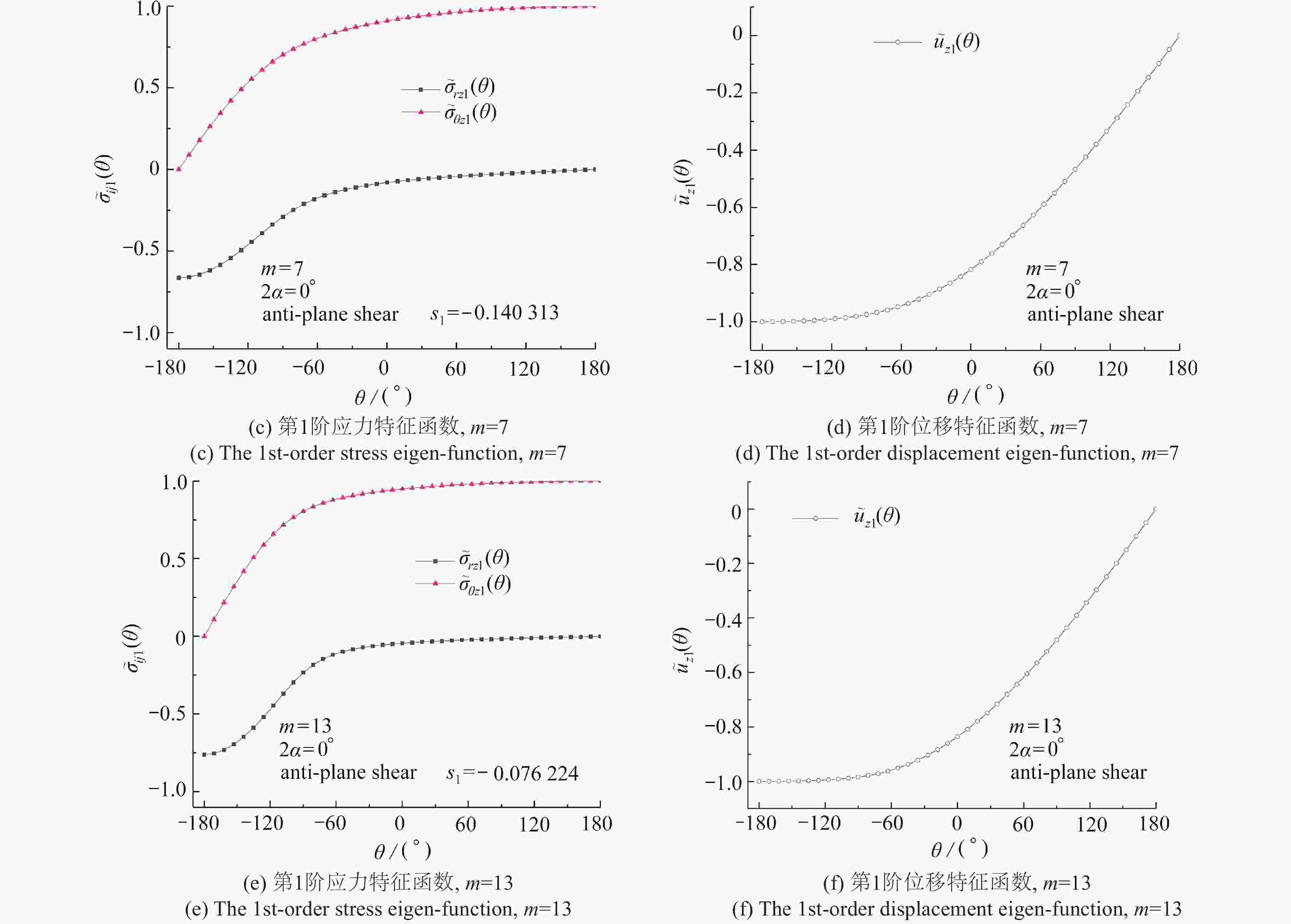
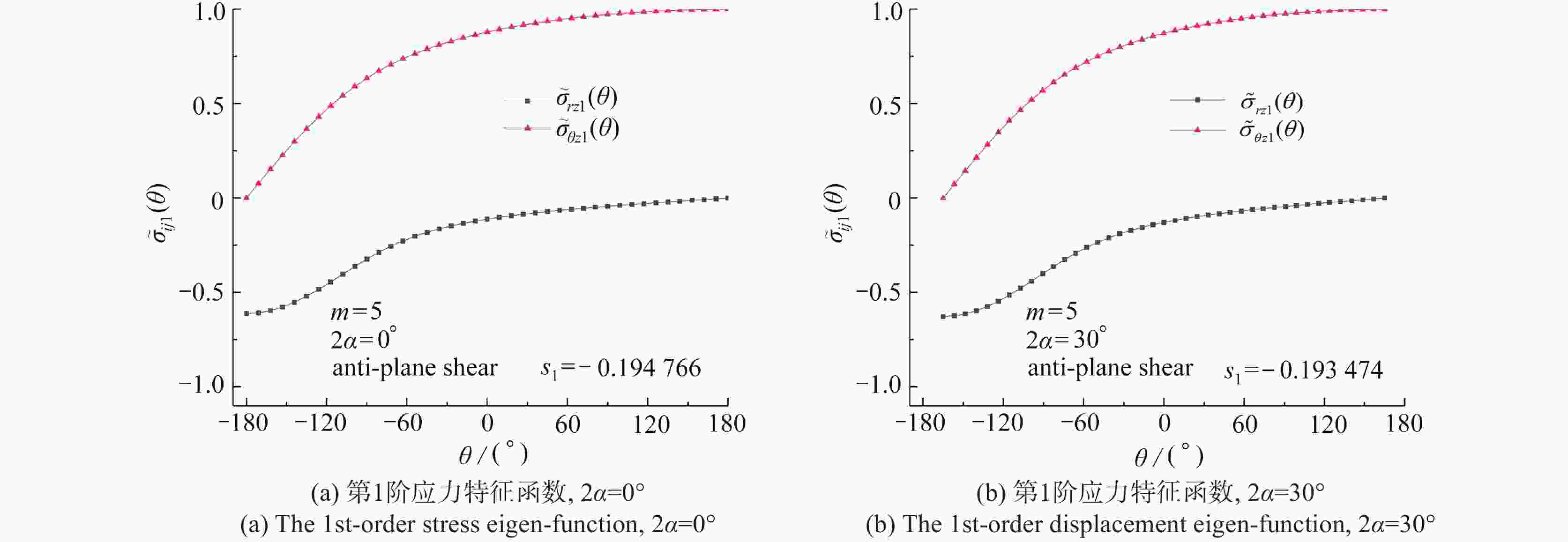
Table 7. Stress exponents $ {s_k} $ of the mode Ⅲ V-notch for various m values and $ {\text{2}}\alpha $ (Q=40)

$ {s_k} $	$ {\text{2}}\alpha $/(°)	m=3	m=5	m=7	m=10	m=13
$ {s_{\text{1}}} $	0	−0.316987	−0.194766	−0.140313	−0.098797	−0.076224
	30	−0.313242	−0.193473	−0.139669	−0.098487	−0.076043
	90	−0.300944	−0.188989	−0.137387	−0.097374	−0.075386
	150	−0.274774	−0.178251	−0.131633	−0.094459	−0.073631
$ {s_{\text{2}}} $	0	−0.049037	−0.026170	−0.017810	−0.012034	−0.009085
	30	−0.000702	0.008722	0.009252	0.008153	0.006996
	90	0.138739	0.116011	0.095654	0.074849	0.061274
	150	0.274774^#	0.321572	0.272393	0.220346	0.184745
$ {s_{\text{3}}} $	0	0.218913^×	0.142426^×	0.104693^×	0.074729^×	0.058054^×
	30	0.311838^×	0.210917^×	0.158173^×	0.114793^×	0.090035^×
	90	0.300944^×	0.421011^×	0.328695^×	0.247072^×	0.197934^×
	150	0.380293	0.534753^#	0.658165^#	0.535151^×	0.443121^×
$ {s_{\text{4}}} $	0	0.285422	0.213317	0.169289	0.129282	0.104644
	30	0.313242^#	0.285697	0.228736	0.176303	0.143628
	90	0.638404	0.50008	0.410023	0.323996	0.268649
	150	0.824322^×	0.821395^×	0.676419^×	0.623227	0.531023

下载: 导出CSV

参考文献(26)

[1]	李聪, 牛忠荣, 胡宗军, 等. 求解双材料裂纹结构全域应力场的扩展边界元法[J]. 应用数学和力学, 2019, 40(8): 926-937. (LI Cong, NIU Zhongrong, HU Zongjun, et al. Computation of total stress fields for cracked bi-material structures with the extended boundary element method[J]. Applied Mathematics and Mechanics, 2019, 40(8): 926-937.(in Chinese)
[2]	HUTCHINSON J W. Singular behavior at the end of a tensile crack in a hardening material[J]. Journal of the Mechanics and Physics of Solids, 1968, 16(1): 13-31. doi: 10.1016/0022-5096(68)90014-8
[3]	RICE J R, ROSENGREN G F. Plane strain deformation near a crack tip in a power-law hardening material[J]. Journal of the Mechanics and Physics of Solids, 1968, 16(1): 1-12. doi: 10.1016/0022-5096(68)90013-6
[4]	KUANG Z, XU X. Stress and strain fields at the tip of a sharp V-notch in a power-hardening material[J]. International Journal of Fracture, 1987, 35: 39-53. doi: 10.1007/BF00034533
[5]	XIA L, WANG T C. Singular behaviour near the tip of a sharp V-notch in a power law hardening material[J]. International Journal of Fracture, 1993, 59(1): 83-93. doi: 10.1007/BF00032219
[6]	LI Y C, WANG T C. High-order asymptotic field of tensile plane-strain nonlinear crack problems[J]. Scientia Sinica(Series A), 1986, 29(9): 941-955.
[7]	SHARMA S M, ARAVAS N. On the development of variable-separable asymptotic elastoplastic solutions for interfacial cracks[J]. International Journal of Solids & Structures, 1993, 30(5): 695-723.
[8]	XIA L, WANG T C, SHIH C F. Higher-order analysis of crack tip fields in elastic power-law hardening materials[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(4): 665-687. doi: 10.1016/0022-5096(93)90022-8
[9]	YUAN F G, YANG S. Crack-tip fields in elastic-plastic material under plane stress mode Ⅰ loading[J]. International Journal of Fracture, 1997, 85(2): 131-155. doi: 10.1023/A:1007361116709
[10]	YANG S, CHAO Y J, SUTTON M A. Higher order asymptotic crack tip fields in a power-law hardening material[J]. Engineering Fracture Mechanics, 1993, 45(1): 1-20. doi: 10.1016/0013-7944(93)90002-A
[11]	CHAO Y J, YANG S. Higher order crack tip fields and its implication for fracture of solids under mode Ⅱ conditions[J]. Engineering Fracture Mechanics, 1996, 55(5): 777-794. doi: 10.1016/0013-7944(96)00054-9
[12]	RICE J R. Stresses due to a sharp notch in a work-hardening elastic-plastic material loaded by longitudinal shear[J]. Journal of Applied Mechanics, 1967, 34(2): 287. doi: 10.1115/1.3607681
[13]	AMAZIGO J C. Fully plastic crack in an infinite body under anti-plane shear[J]. International Journal of Solids and Structures, 1974, 10(9): 1003-1015. doi: 10.1016/0020-7683(74)90008-0
[14]	YANG S, YUAN F G, CAI X. Higher orderasymptotic elastic-plastic crack-tip fields under antiplane shear[J]. Engineering Fracture Mechanics, 1996, 54(3): 405-422. doi: 10.1016/0013-7944(95)00191-3
[15]	YANG S, YUAN F G, CHIANG M Y M. Analytical forms of higher-order asymptotic elastic-plastic crack-tip fields in a linear hardening material under antiplane shear[J]. International Journal of Fracture, 1996, 80(1): 59-71. doi: 10.1007/BF00036480
[16]	YUAN F G, YANG S. Analytical solutions of fully plastic crack-tip higher order fields under antiplane shear[J]. International Journal of Fracture, 1994, 69(1): 1-26.
[17]	WANG T J, KUANG Z B. Higher order asymptotic solutions of V-notch tip fields for damaged nonlinear materials under antiplane shear loading[J]. International Journal of Fracture, 1999, 96(4): 303-329. doi: 10.1023/A:1018657316810
[18]	ZAPPALORTO M, LAZZARIN P. Analytical study of the elastic-plastic stress fields ahead of parabolic notches under antiplane shear loading[J]. International Journal of Fracture, 2007, 148(2): 139-154. doi: 10.1007/s10704-008-9185-7
[19]	LAZZARIN P, ZAPPALORTO M. Plastic notch stress intensity factors for pointed V-notches under antiplane shear loading[J]. International Journal of Fracture, 2008, 152(1): 1-25. doi: 10.1007/s10704-008-9260-0
[20]	ZAPPALORTO M, LAZZARIN P. A unified approach to the analysis of nonlinear stress and strain fields ahead of mode Ⅲ-loaded notches and cracks[J]. International Journal of Solids and Structures, 2010, 47(6): 851-864. doi: 10.1016/j.ijsolstr.2009.11.021
[21]	ARAVAS N, BLAZO D H. Higher order terms in asymptotic elastoplastic mode Ⅲ crack tip solutions[J]. Acta Mechanica, 1991, 90(1/4): 139-153.
[22]	LOGHIN A, ZHANG N, JOSEPH P F. A nonlinear finite element eigenanalysis of antiplane shear including higher order terms[J]. Engineering Fracture Mechanics, 2000, 66(5): 441-454. doi: 10.1016/S0013-7944(00)00031-X
[23]	ZHANG N, JOSEPH P F. A nonlinear finite element eigenanalysis of singular stress fields in bimaterial wedges for plane strain[J]. International Journal of Fracture, 1998, 94(3): 299-319.
[24]	LOGHIN A, JOSEPH P F. Asymptotic solutions for mixed mode loading of cracks and wedges in power law hardening materials[J]. Engineering Fracture Mechanics, 2001, 68(14): 1511-1534. doi: 10.1016/S0013-7944(01)00050-9
[25]	PATWARDHAN P A, NALAVDE R A, KUJAWSKI D. An estimation of Ramberg-Osgood constants for materials with and without Loder’s strain using yield and ultimate strengths[J]. Procedia Structure Integrity, 2019, 17: 750-757. doi: 10.1016/j.prostr.2019.08.100
[26]	NIU Z R, GE D L, CHENG C Z, et al. Evaluation of the stress singularities of plane V-notches in bonded dissimilar materials[J]. Applied Mathematical Modelling, 2009, 33(3): 1776-1792. doi: 10.1016/j.apm.2008.03.007