Anti-Controlling Codimension-2 Bifurcation of Discrete Dynamical Systems in 1 ∶ 2 Resonance
-
摘要:
从分岔反控制的角度设计了一套非线性反馈控制策略,来实现离散动力系统1∶2共振情形下余维二分岔的各种分岔解。首先,针对传统分岔准则在确定高余维分岔点时存在的局限性,建立了一个1∶2共振情形下的余维二分岔的新显式准则,基于这个显式准则通过设计线性控制增益来确保此类余维二分岔的存在性。然后,推导了1∶2共振的中心流形,并基于范式方法通过设计非线性控制增益,分析了1∶2共振情形下余维二分岔解的类型和稳定性。最后,以一个Arneodo-Coullet-Tresser映射为例,在指定的参数点处通过控制实现了具有1∶2共振分岔特性的各种分岔解,进一步验证了理论分析。
-
关键词:
- 1∶2共振情形下的余维二分岔 /
- 显式准则 /
- 分岔反控制 /
- 离散动力系统
Abstract:A set of nonlinear feedback control strategies were designed to realize the bifurcation solutions of codimensional bifurcations in discrete dynamical systems with 1∶2 resonance from the perspective of bifurcation anti-controlling. Firstly, aimed at the limitation of traditional bifurcation criteria for determination of high codimensional bifurcation points, a new explicit criterion for codimension-2 bifurcation in 1∶2 resonance was proposed. Based on this explicit criterion, the linear control gain was designed to ensure the existence of such codimension-2 bifurcation. Then, the central manifold of 1∶2 resonance was derived. Based on the normal form method, the types and stability of codimension-2 bifurcation solutions in 1∶2 resonance were analyzed through design of nonlinear control gain. Finally, an Arneodo-Coullet-Tresser mapping was taken as an example, and various bifurcation solutions with 1∶2 resonance bifurcation properties were realized by control at the specified parameter points, to further validate the theoretical analysis.
-
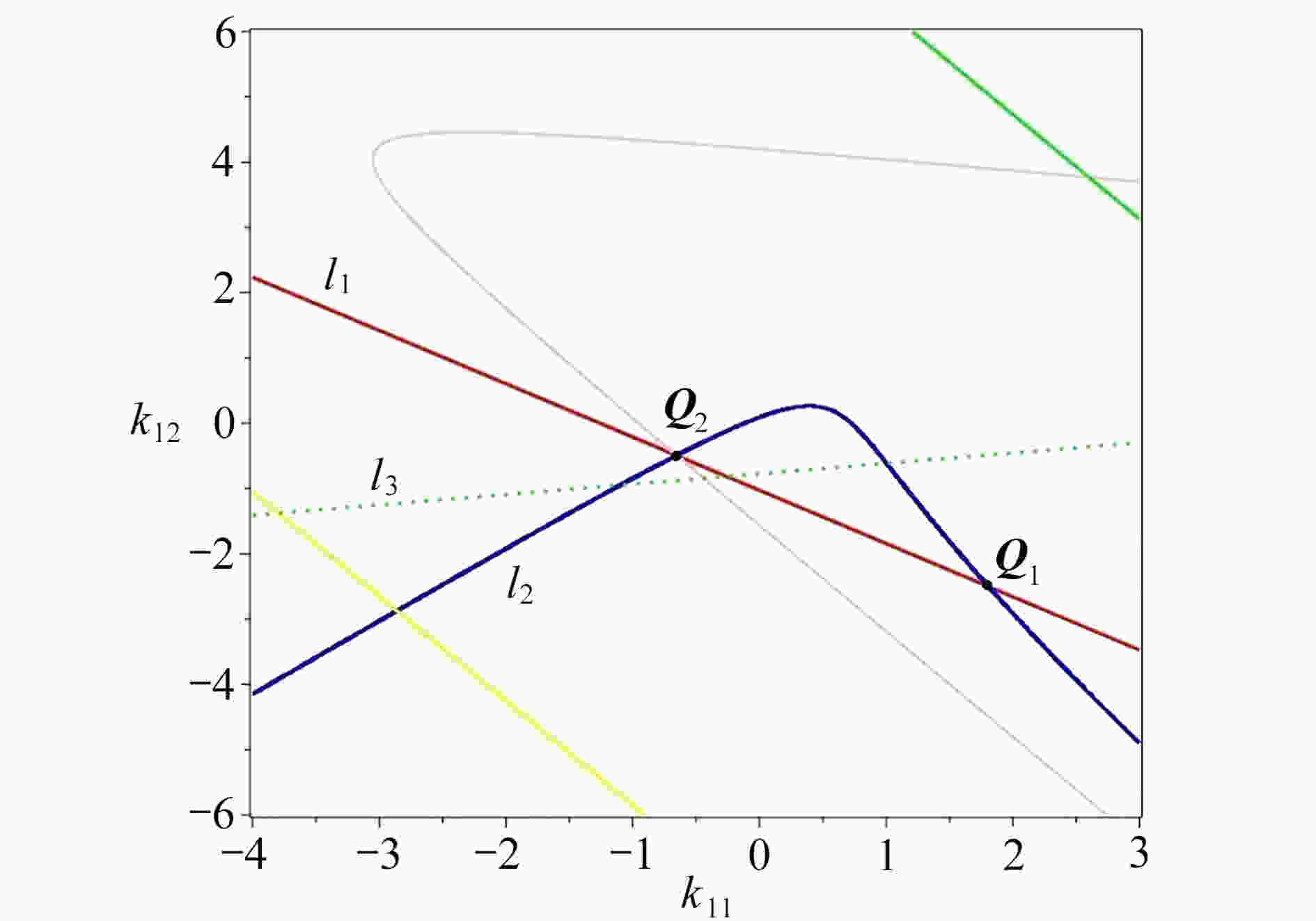
图 3 控制系统(29)对应情形5形如式(20)的范式映射的分岔图:(a)
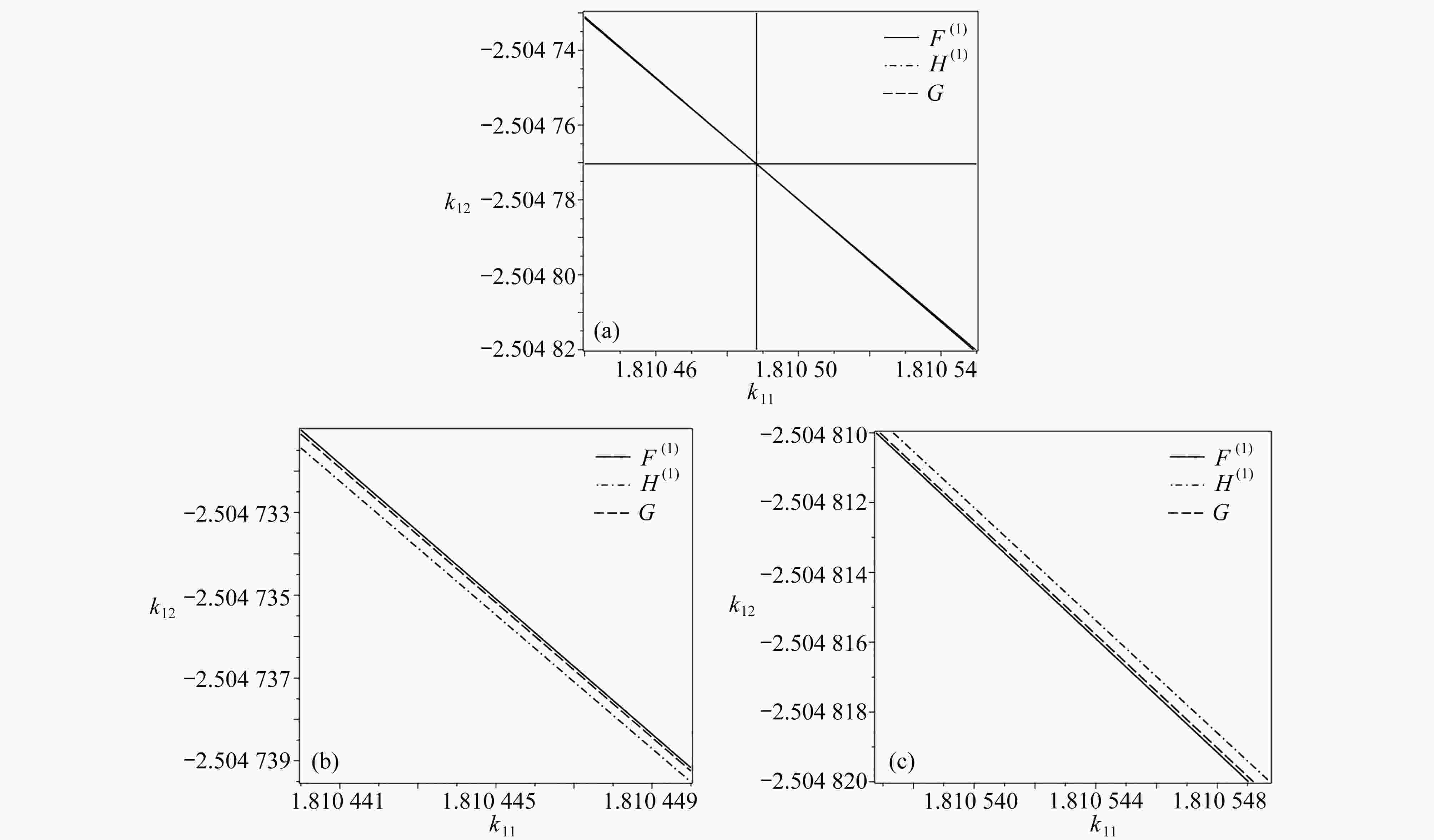
${\tilde{C}}(0, {{\boldsymbol{K}}_{{\rm{NL}}}}) > 0$ 时,系统(29)对应的分支图;(b) 对应于图3(a)分岔点上半部分的局部放大图;(c) 对应于图3(a)分岔点下半部分的局部放大图Figure 3. Bifurcation diagrams of the normal form mapping like eq. (20) of control system (29) corresponding to case 5: (a) the bifurcation diagram for system (29),
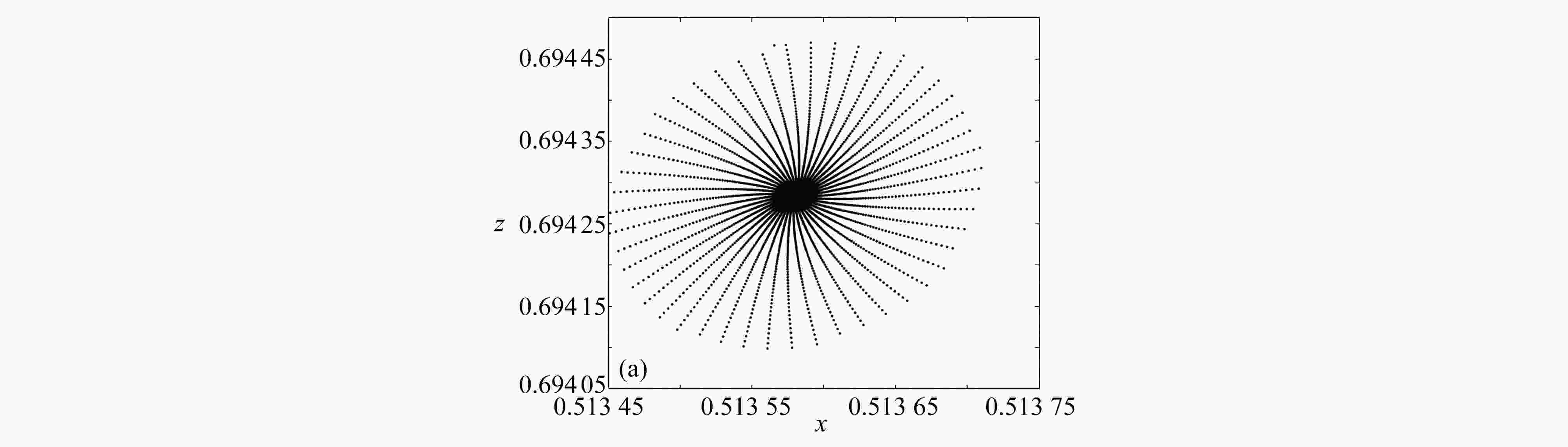
$\tilde{C}\left(0, {{\boldsymbol{K}}_{{\rm{NL}}}}\right) > 0$ ; (b) the local enlargement of the upper half of the bifurcation points in fig. 3(a); (c) the local enlargement of the lower half of the bifurcation points in fig. 3(a)图 4 对应于图3所示分岔图的相图:(a) 在
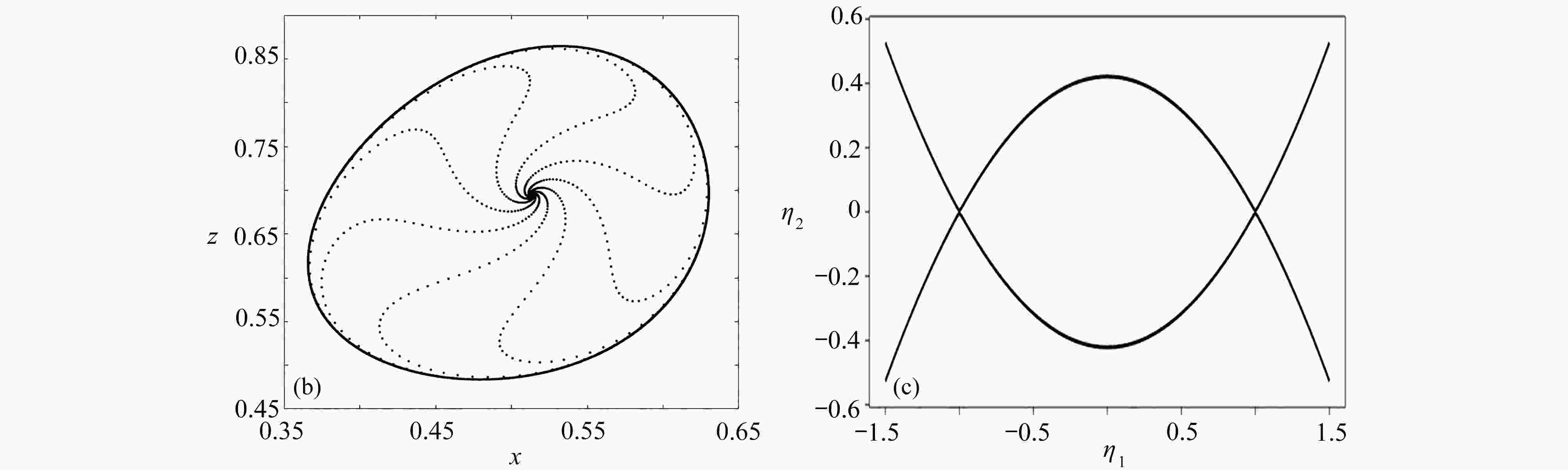
$\left(k_{11}, k_{12}\right)={{\boldsymbol{Q}}_{1}}+(-0.08,0.15)$ 处的稳定点;(b) 在$\left(k_{11}, k_{12}\right)={{\boldsymbol{Q}}_{1}}+(-0.1,-0.01)$ 处的不变圈;(c) 异宿分支曲线G上的异宿轨道Figure 4. Phase diagrams corresponding to the bifurcation diagrams shown in fig. 3: (a) the fixed point at
$\left(k_{11}, k_{12}\right)={{\boldsymbol{Q}}_{1}}+(-0.08,0.15)$ ; (b) the invariable circle at$\left(k_{11}, k_{12}\right)={{\boldsymbol{Q}}_{1}}+(-0.1,-0.01) $ ; (c) the heterotropic orbit on heterotropic curve G图 5 控制系统(29)对应情形6形如式(20)的范式映射的分岔图:(a)
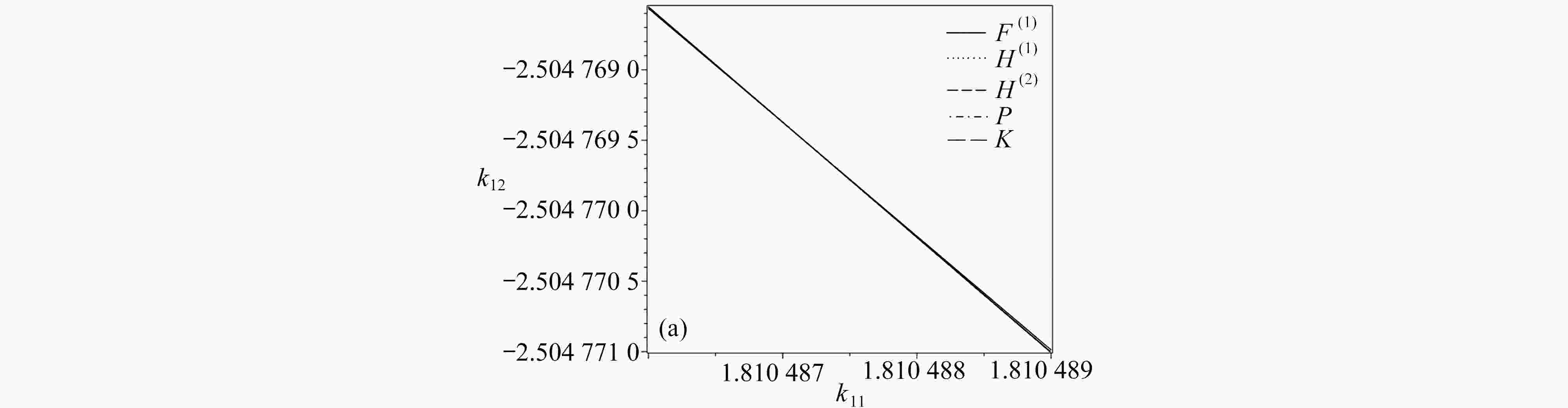
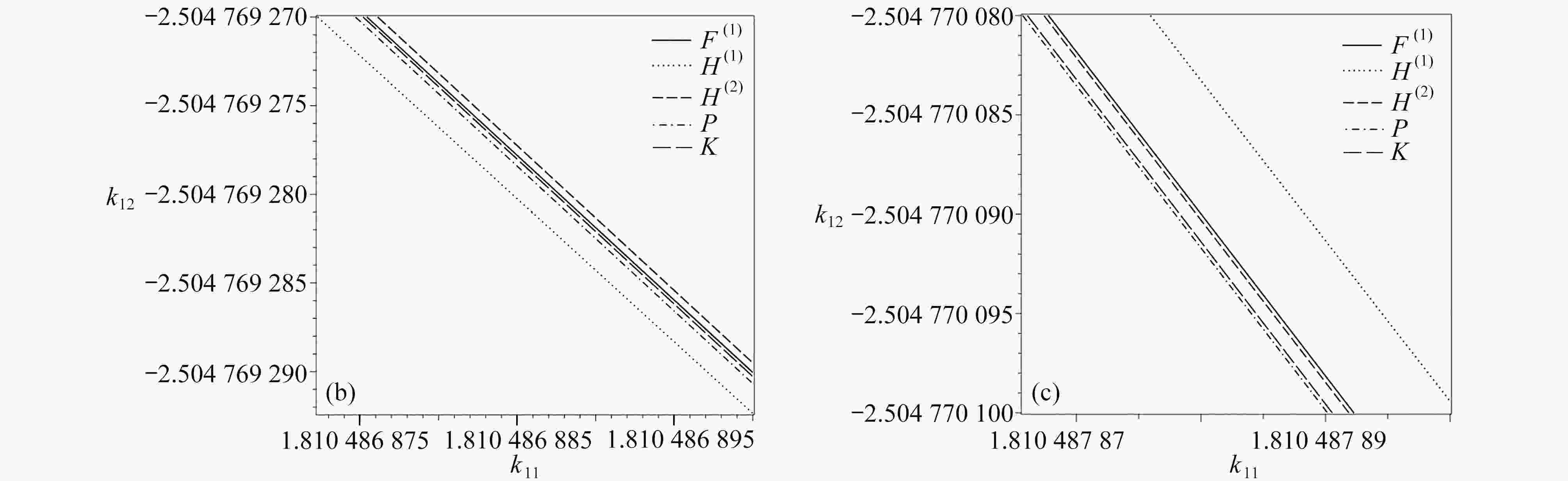
$\tilde{C}\left(0, {{\boldsymbol{K}}_{{\rm{NL}}}}\right) < 0$ 时,系统(29)对应的分支图;(b) 对应于图5(a)分岔点上半部分的局部放大图;(c) 对应于图5(a)分岔点下半部分的局部放大图Figure 5. Bifurcation diagrams of the normal form mapping like eq. (20) of control system (29) corresponding to case 6: (a) the bifurcation diagram of system (29),
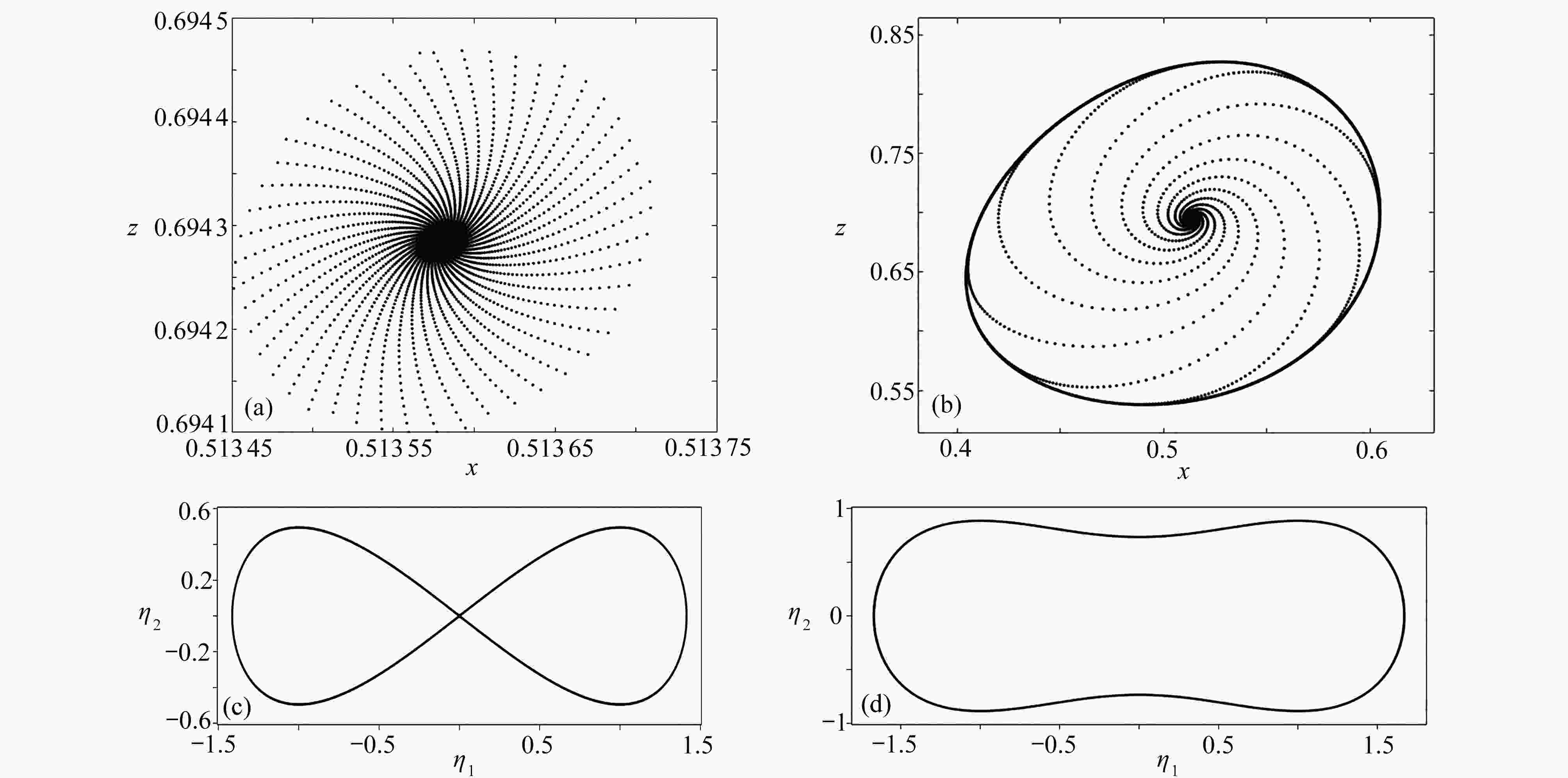
$\tilde{C}\left(0, {{\boldsymbol{K}}_{{\rm{NL}}}}\right) < 0$ ; (b) the local enlargement of the upper half of the bifurcation points in fig. 5(a); (c) the local enlargement of the lower half of the bifurcation points in fig. 5(a)图 6 对应于图5所示分岔图的相图:(a) 在
$\left(k_{11}, k_{12}\right)=\boldsymbol{Q}_{1}+(-0.11,0.12)$ 处的稳定点;(b) 在$\left(k_{11}, k_{12}\right)=\boldsymbol{Q}_{1}+(-0.1,-0.05)$ 处的不变圈;(c) 同宿分支曲线P上的同宿轨道;(d) 环的折分支曲线K上的轨道Figure 6. Phase diagrams corresponding to the bifurcation diagrams shown in fig. 5: (a) the fixed point at
$\left(k_{11}, k_{12}\right)=\boldsymbol{Q}_{1}+(-0.11,0.12) $ ; (b) the invariable circle at$\left(k_{11}, k_{12}\right)=\boldsymbol{Q}_{1}+(-0.1,-0.05) $ ; (c) the homoclinic orbit on homoclinic curve P; (d) the orbit on the folded branch curve of ring K -
[1] AGLIARI A, NAIMZADA A K, PECORA N. Nonlinear dynamics of a Cournot duopoly game with differentiated products[J]. Applied Mathematics and Computation, 2016, 281: 1-15. doi: 10.1016/j.amc.2016.01.045 [2] AGLIARI A, NAIMZADA A, PECORA N. Bifurcation structures of a cobweb model with memory and competing technologies[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 58: 78-91. doi: 10.1016/j.cnsns.2017.04.008 [3] ZHANG L M, ZHANG C F, HE Z R. Codimension-one and codimension-two bifurcations of a discrete predator-prey system with strong Allee effect[J]. Mathematics and Computers in Simulation, 2019, 162: 155-178. doi: 10.1016/j.matcom.2019.01.006 [4] CHEN Q L, TENG Z D. Codimension-two bifurcation analysis of a discrete predator-prey model with nonmonotonic functional response[J]. Journal of Difference Equations and Applications, 2017, 23(12): 2093-2115. doi: 10.1080/10236198.2017.1395418 [5] YUAN L G, YANG Q G. Bifurcation, invariant curve and hybrid control in a discrete-time predator-prey system[J]. Applied Mathematical Modelling, 2015, 39(8): 2345-2362. doi: 10.1016/j.apm.2014.10.040 [6] PECORA N. Analysis of 1∶4 resonance in a monopoly model with memory[J]. Chaos, Solitons and Fractals, 2018, 110: 95-104. doi: 10.1016/j.chaos.2018.03.005 [7] REN J L, YU L P. Codimension-two bifurcation, chaos and control in a discrete-time information diffusion model[J]. Journal of Nonlinear Science, 2016, 26(6): 1895-1931. doi: 10.1007/s00332-016-9323-8 [8] LI B, HE Q Z. Bifurcation analysis of a two-dimensional discrete Hindmarsh-Rose type model[J]. Advances in Difference Equations, 2019(1): 124. doi: 10.1186/s13662-019-2062-z [9] CHEN D S, WANG H O, CHEN G R. Anti-control of Hopf bifurcations[J]. IEEE Transactions on Circuits and Systems I, 2001, 48(6): 661-672. doi: 10.1109/81.928149 [10] WEN G L, WANG Q G, CHIU M S. Delay feedback control for interaction of Hopf and period doubling bifurcations in discrete-time systems[J]. International Journal of Bifurcation and Chaos, 2006, 16(1): 101-112. doi: 10.1142/S0218127406014617 [11] 伍新, 文桂林, 徐慧东, 等. 惯性式冲击振动落砂机周期倍化分岔的反控制[J]. 固体力学学报, 2015, 36(1): 28-34. (WU Xin, WEN Guilin, XU Huidong, et al. Anti-controlling period-doubling bifurcation of an inertial impact shaker system[J]. Chinese Journal of Solid Mechanics, 2015, 36(1): 28-34.(in Chinese) [12] 张玲梅, 张建文, 吴润衡. 具有对应分段系统和指数系统的新混沌系统的Hopf分岔控制研究[J]. 物理学报, 2014, 63(16): 160505. (ZHANG Lingmei, ZHANG Jianwen, WU Runheng. Anti-control of Hopf bifurcation in the new chaotic system with piecewise system and exponential system[J]. Acta Physica Sinica, 2014, 63(16): 160505.(in Chinese) doi: 10.7498/aps.63.160505 [13] 刘素华, 唐驾时. 四维Qi系统零平衡点的Hopf分岔反控制[J]. 物理学报, 2008, 57(10): 6162-6168. (LIU Suhua, TANG Jiashi. Anti-control of Hopf bifurcation at zero equilibrium of 4D Qi system[J]. Acta Physica Sinica, 2008, 57(10): 6162-6168.(in Chinese) doi: 10.3321/j.issn:1000-3290.2008.10.018 [14] WEN G L, XU D L, XIE J H. Controlling Hopf bifurcations of discrete-time systems in resonance[J]. Chaos, Solitons and Fractals, 2005, 23(5): 1865-1877. doi: 10.1016/S0960-0779(04)00451-5 [15] 伍新, 文桂林, 徐慧东, 等. 三自由度含间隙碰撞振动系统Neimark-Sacker分岔的反控制[J]. 物理学报, 2015, 64(20): 200504. (WU Xin, WEN Guilin, XU Huidong, et al. Anti-controlling Neimark-Sacker bifurcation of a three-degree-of-freedom vibration system with clear-ance[J]. Acta Physica Sinica, 2015, 64(20): 200504.(in Chinese) doi: 10.7498/aps.64.200504 [16] 徐慧东, 文桂林, 伍新, 等. 三自由度含间隙碰撞振动系统Poincaré映射Hopf-Hopf交互分岔的反控制[J]. 振动工程学报, 2015, 28(6): 952-959. (XU Huidong, WEN Guilin, WU Xin, et al. Anti-controlling Hopf-Hopf interaction bifurcations on Poincaré map of a three-degree-of-freedom vibro-impact system with clearance[J]. Journal of Vibration Engineering, 2015, 28(6): 952-959.(in Chinese) [17] WEN G L. Criterion to identify Hopf bifurcations in maps of arbitrary dimension[J]. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2005, 72(2): 026201. doi: 10.1103/PhysRevE.72.026201 [18] XU H D, WEN G L. Alternative criterion for investigation of pitchfork bifurcations of limit cycle in relay feedback systems[J]. Journal of Computational and Nonlinear Dynamics, 2014, 9(3): 031004. doi: 10.1115/1.4025744 [19] YAO S J. New Bifurcation critical criterion of Flip-Neimark-Sacker bifurcations for two-parameterized family of n-dimensional discrete systems[J]. Discrete Dynamics in Nature and Society, 2012, 2012: 264526. doi: 10.1155/2012/264526 [20] KUZNETSOV Y A. Elements of Applied Bifurcation Theory[M]. 3rd ed. New York: Springer-Verlag, 2004. [21] WEN G L, CHEN S J, JIN Q T. A new criterion of period-doubling bifurcation in maps and its application to an inertial impact shaker[J]. Journal of Sound and Vibration, 2008, 311(1/2): 212-223. [22] LASALLE J P. The Stability and Control of Discrete Processes[M]. Berlin: Springer-Verlag, 1986. [23] JURY E I, PAVLIDIS T. Stability and aperiodicity constraints for system design[J]. IEEE Transactions on Circuit Theory, 1963, 10(1): 137-141. doi: 10.1109/TCT.1963.1082100 [24] KUZNETSOV Y A, MEIJER H G E, VAN VEEN L. The fold-flip bifurcation[J]. International Journal of Bifurcation and Chaos, 2004, 14(7): 2253-2282. doi: 10.1142/S0218127404010576 [25] DU B S, LI M C, MALKIN M I. Topological horseshoes for Arneodo-Coullet-Tresser maps[J]. Regular and Chaotic Dynamics, 2006, 11(2): 181-190. doi: 10.1070/RD2006v011n02ABEH000344 -




 下载:
下载:

















 渝公网安备50010802005915号
渝公网安备50010802005915号