Theoretical Analysis on Dynamic Stability of Rotating Pipes Conveying Fluid
-
摘要:
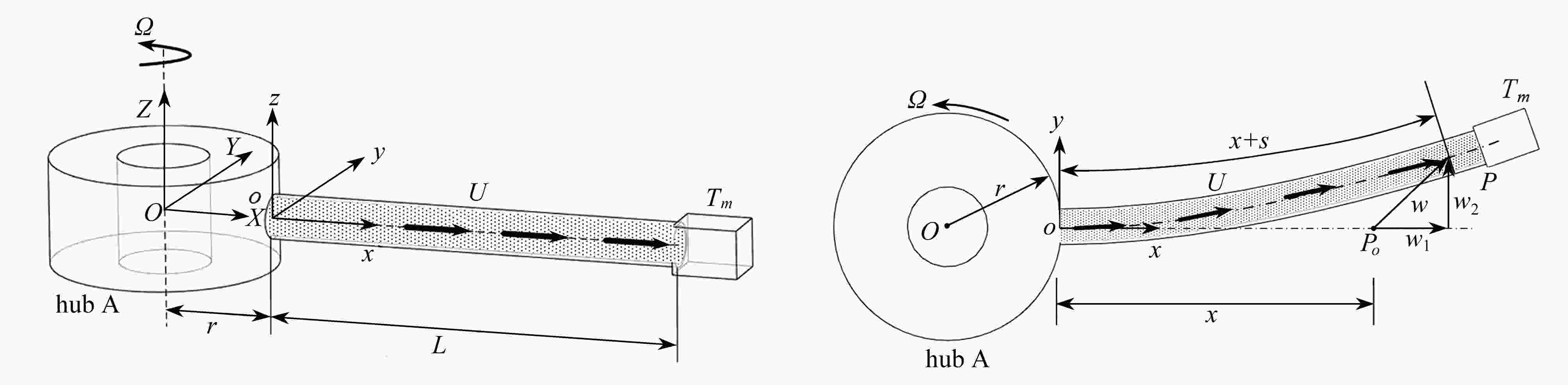
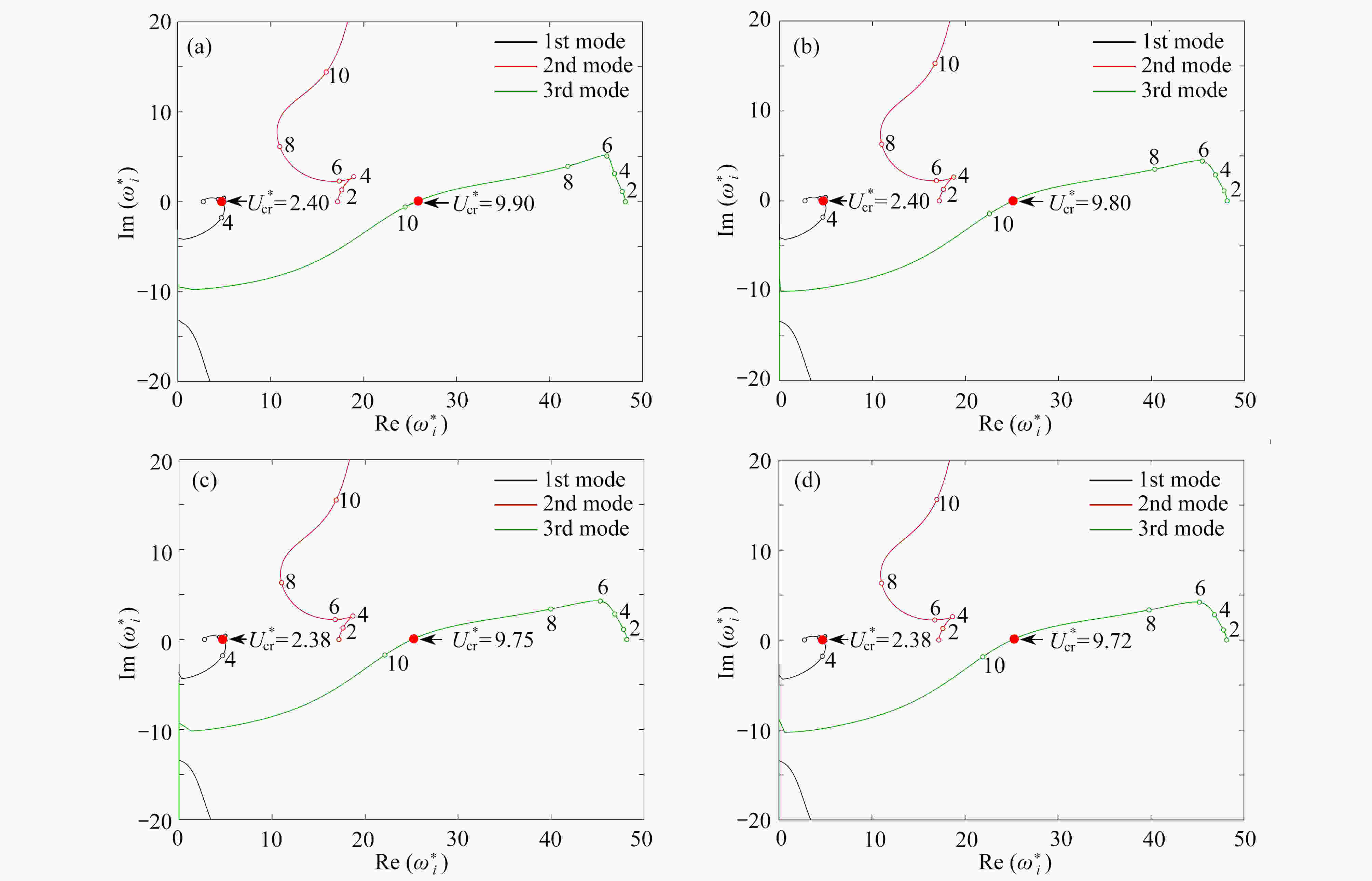
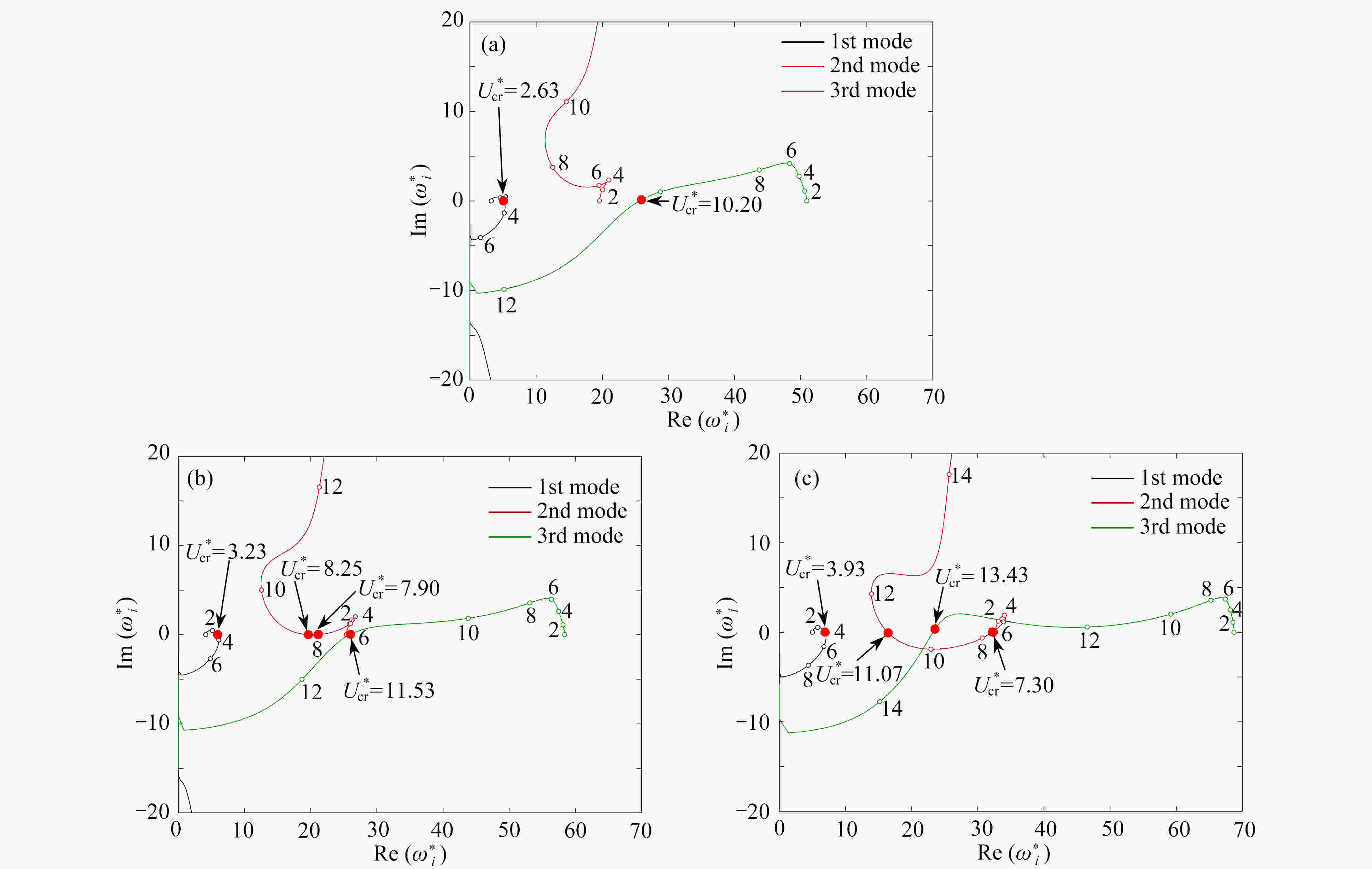
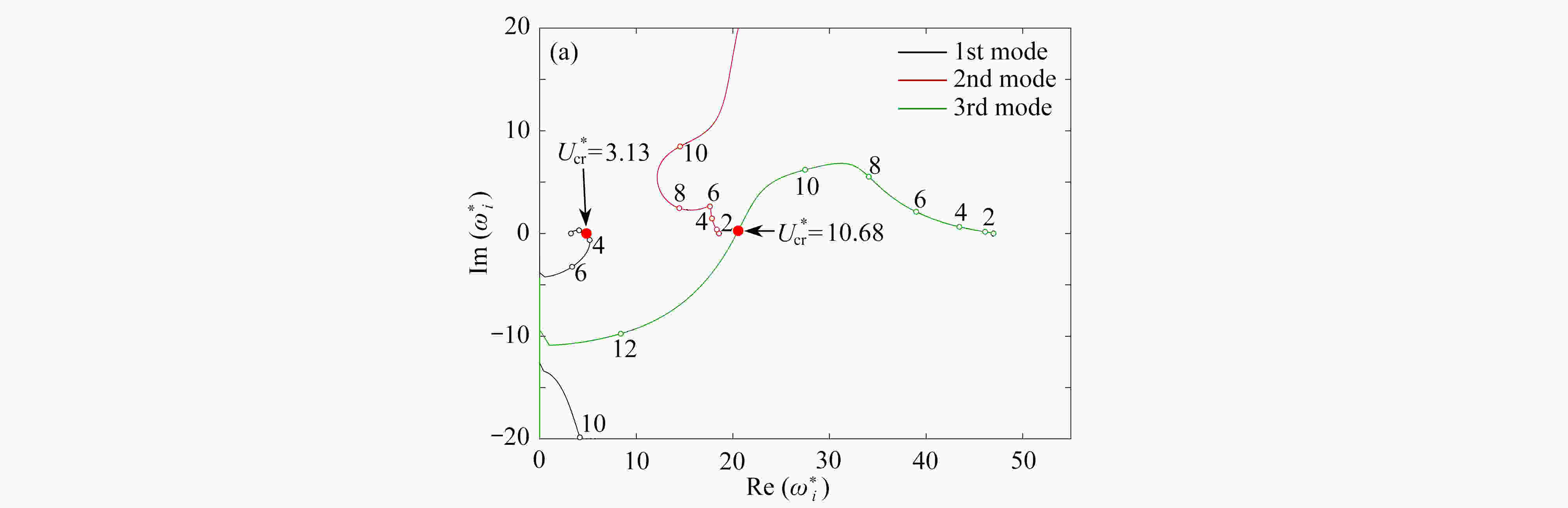
基于Lagrange原理和假设模态法建立了旋转输液管的动力学模型。通过降阶升维的方法求解系统的特征值问题,并分析了旋转输液管自由振动特性。得到了不同端部集中质量和转速下,系统特征值随流速升高的演变轨迹。揭示了临界流速随系统参数的变化规律。研究发现,内部流体的流动对旋转输液管动力学特性存在显著影响。在某些参数组合下,系统低阶模态能够形成不同形式的内共振关系。预示了旋转输液管模型蕴含丰富的动力学现象。
-
关键词:
- 旋转 /
- 输液管 /
- 自由振动 /
- 假设模态法 /
- Lagrange方程
Abstract:The dynamic model was built for rotating pipes conveying fluid based on the Lagrange principle and the assumed mode method. The eigenvalue problem of the system was solved via the method of “reducing the order and increasing the dimension”. The free vibration characteristics of the rotating pipe conveying fluid were analyzed. The variations of the eigenvalue trajectories with the fluid velocity were illustrated under different tip masses and rotating speeds. The effects of system parameters on the critical fluid velocity were revealed. It is found that, the flowing fluid has significant effects on the dynamic characteristics of the rotating pipe. Different internal resonances between the 1st several modes of the system could exist under certain parameter conditions. The work reveals rich dynamic phenomena of the rotating pipe conveying fluid.
-
Key words:
- rotation /
- pipe conveying fluid /
- free vibration /
- assumed mode method /
- Lagrange equation
-
表 1 系统参数设置
Table 1. System parameter values
L/m E/Pa r/m Rout /m Rin /m ρp /(kg·m−3) ρf /(kg·m−3) 1 4.957×107 0.5 0.025 0.02 2 766 1 000 表 2 系统第一阶无量纲固有频率本文计算值与文献对比(ρf = 0)
Table 2. Comparison of the 1st natural frequencies obtained from the present study and the reference (ρf = 0)
Ω* = 2 Ω* = 10 r/L = 0 r/L = 1 r/L = 5 r/L = 0 r/L = 1 r/L = 5 this paper ω* 3.619 4.397 6.642 4.951 12.996 27.152 ref. [33] ω* 3.62 4.40 6.64 4.97 13.1 27.3 error δ/% 0.028 0.068 0.030 0.382 0.794 0.542 -
[1] 蒋洪德, 任静, 李雪英, 等. 重型燃气轮机现状与发展趋势[J]. 中国电机工程学报, 2014, 34(29): 5096-5102. (JIANG Hongde, REN Jing, LI Xueying, et al. Status and development trend of the heavy duty gas turbine[J]. Proceedings of the CSEE, 2014, 34(29): 5096-5102.(in Chinese) [2] 王超, 苟学科, 段英, 等. 航空发动机涡轮叶片温度测量综述[J]. 红外与毫米波学报, 2018, 37(4): 501-512. (WANG Chao, GOU Xueke, DUAN Ying, et al. A review of aero-engine turbine blade temperature measurement[J]. Journal of Infrared and Millimeter Waves, 2018, 37(4): 501-512.(in Chinese) doi: 10.11972/j.issn.1001-9014.2018.04.019 [3] 李广超, 于全朋, 张魏, 等. 吹风比对涡轮叶片尾缘气膜冷却效率影响[J]. 热力发电, 2018, 47(10): 58-65. (LI Guangchao, YU Quanpeng, ZHANG Wei, et al. Effect of blowing ratio on film cooling efficiency of trailing edge on turbine blade[J]. Thermal Power Generation, 2018, 47(10): 58-65.(in Chinese) [4] OH Y, YOO H H. Vibration analysis of a rotating pre-twisted blade considering the coupling effects of stretching, bending, and torsion[J]. Journal of Sound and Vibration, 2018, 431: 20-39. doi: 10.1016/j.jsv.2018.05.030 [5] HODGES D Y, RUTKOWSKI M Y. Free-vibration analysis of rotating beams by a variable-order finite-element method[J]. AIAA Journal, 1981, 19(11): 1459-1466. doi: 10.2514/3.60082 [6] 张伟, 冯志青, 曹东兴. 航空发动机叶片非线性动力学分析[J]. 动力学与控制学报, 2012, 10(3): 213-221. (ZHANG Wei, FENG Zhiqing, CAO Dongxing. Analysis on nonlinear dynamics of the aero-engine blade[J]. Journal of Dynamics and Control, 2012, 10(3): 213-221.(in Chinese) [7] ZHANG W, NIU Y, BEHDINAN K. Vibration characteristics of rotating pretwisted composite tapered blade with graphene coating layers[J]. Aerospace Science and Technology, 2020, 98: 105644. doi: 10.1016/j.ast.2019.105644 [8] YAO M H, NIU Y, HAO Y X. Nonlinear dynamic responses of rotating pretwisted cylindrical shells[J]. Nonlinear Dynamics, 2019, 95(1): 151-174. doi: 10.1007/s11071-018-4557-7 [9] 郑彤, 章定国, 廖连芳, 等. 航空发动机叶片刚柔耦合动力学分析[J]. 机械工程学报, 2014, 50(23): 42-49. (ZHENG Tong, ZHANG Dingguo, LIAO Lianfang, et al. Rigid-flexible coupling dynamic analysis of aero-engine blades[J]. Journal of Mechanical Engineering, 2014, 50(23): 42-49.(in Chinese) doi: 10.3901/JME.2014.23.042 [10] ZHANG B, LI Y M. Nonlinear vibration of rotating pre-deformed blade with thermal gradient[J]. Nonlinear Dynamics, 2016, 86(1): 459-478. doi: 10.1007/s11071-016-2900-4 [11] ZHANG B, ZHANG Y L, YANG X D, et al. Saturation and stability in internal resonance of a rotating blade under thermal gradient[J]. Journal of Sound and Vibration, 2019, 440(3): 34-50. [12] ZHANG B, DING H, CHEN L Q. Three to one internal resonances of a pre-deformed rotating beam with quadratic and cubic nonlinearities[J]. International Journal of Non-Linear Mechanics, 2020, 126: 103552. doi: 10.1016/j.ijnonlinmec.2020.103552 [13] OH Y, YOO H H. Thermo-elastodynamic coupled model to obtain natural frequency and stretch characteristics of a rotating blade with a cooling passage[J]. International Journal of Mechanical Sciences, 2020, 165: 105194. doi: 10.1016/j.ijmecsci.2019.105194 [14] BENJAMIN T. Dynamics of a system of articulated pipes conveying fluid, Ⅰ: theory[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1961, 261: 457-486. [15] GREGORY R W P, PAIDOUSSIS M P. Unstable oscillation of tubular cantilevers conveying fluid, Ⅰ: theory[J]. Proceedings of the Royal Society of London(Series A) : Mathematical and Physical Sciences, 1966, 293(1435): 512-527. doi: 10.1098/rspa.1966.0187 [16] 王乙坤, 王琳. 分布式运动约束下悬臂输液管的参数共振研究[J]. 力学学报, 2019, 51(2): 558-568. (WANG Yikun, WANG Lin. Parametric resonance of a cantilevered pipe conveying fluid subjected to distributed motion constraints[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 558-568.(in Chinese) doi: 10.6052/0459-1879-18-295 [17] 易浩然, 周坤, 代胡亮, 等. 含集中质量悬臂输流管的稳定性与模态演化特性研究[J]. 力学学报, 2020, 52(6): 1800-1810. (YI Haoran, ZHOU Kun, DAI Huliang, et al. Stability and mode evolution characteristics of a cantilevered fluid-conveying pipe attached with the lumped mass[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1800-1810.(in Chinese) doi: 10.6052/0459-1879-20-280 [18] 毛晓晔, 丁虎, 陈立群. 3∶1内共振下超临界输液管受迫振动响应[J]. 应用数学和力学, 2016, 37(4): 345-351. (MAO Xiaoye, DING Hu, CHEN Liqun. Forced vibration responses of supercritical fluid-conveying pipes in 3∶1 internal resonance[J]. Applied Mathematics and Mechanics, 2016, 37(4): 345-351.(in Chinese) doi: 10.3879/j.issn.1000-0887.2016.04.002 [19] 黄慧春, 张艳雷, 陈立群. 受迫振动的超临界输液管galerkin数值模拟[J]. 应用数学和力学, 2014, 35(10): 1100-1106. (HUANG Huichun, ZHANG Yanlei, CHEN Liqun. A Galerkin numerical method for the pipe conveying supercritical fluid under forced vibration[J]. Applied Mathematics and Mechanics, 2014, 35(10): 1100-1106.(in Chinese) doi: 10.3879/j.issn.1000-0887.2014.10.004 [20] 黄玉盈, 钱勤, 徐鉴, 等. 输液管的非线性振动、分叉与混沌: 现状与展望[J]. 力学进展, 1998, 28(1): 30-42. (HUANG Yuying, QIAN Qing, XU Jian, et al. Advances and trends of nonlinear dynamics of pipes conveying fluid[J]. Advances in Mechanics, 1998, 28(1): 30-42.(in Chinese) doi: 10.3321/j.issn:1000-0992.1998.01.003 [21] 金基铎, 杨晓东, 邹光胜. 两端支承输流管道的稳定性和临界流速分析[J]. 机械工程学报, 2006, 42(11): 131-136. (JlN Jiduo, YANG Xiaodong, ZOU Guangsheng. Stability and critical flow velocity of supported pipes conveying fluid[J]. Chinese Journal of Mechanical Engineering, 2006, 42(11): 131-136.(in Chinese) doi: 10.3321/j.issn:0577-6686.2006.11.021 [22] 徐鉴, 杨前彪. 流体诱发水平悬臂输液管的内共振和模态转换(Ⅰ)[J]. 应用数学和力学, 2006, 27(7): 819-824. (XU Jian, YANG Qianbiao. Flow-induced internal resonances and mode exchange in horizontal cantilevered pipe conveying fluid(Ⅰ)[J]. Applied Mathematics and Mechanics, 2006, 27(7): 819-824.(in Chinese) doi: 10.3321/j.issn:1000-0887.2006.07.009 [23] 徐鉴, 杨前彪. 流体诱发水平悬臂输液管的内共振和模态转换(Ⅱ)[J]. 应用数学和力学, 2006, 27(7): 825-832. (XU Jian, YANG Qianbiao. Flow-induced internal resonances and mode exchange in horizontal cantilevered pipe conveying fluid(Ⅱ)[J]. Applied Mathematics and Mechanics, 2006, 27(7): 825-832.(in Chinese) doi: 10.3321/j.issn:1000-0887.2006.07.010 [24] 王琳, 匡友弟, 黄玉盈, 等. 输液管振动与稳定性研究的新进展: 从宏观尺度到微纳米尺度[J]. 固体力学学报, 2010, 31(5): 481-495. (WANG Lin, KUANG Youdi, HUANG Yuying, et al. Recent development on vibration and stability of pipes conveying fluid: from macro-scale to micro-and nano-scales[J]. Chinese Journal of Solid Mechanics, 2010, 31(5): 481-495.(in Chinese) [25] LIAN F, YANG X D, ZHANG W, et al. Nonlinear free vibration of spinning viscoelastic pipes conveying fluid[J]. International Journal of Applied Mechanics, 2018, 10(7). DOI: 10.1142/S175882511850076X. [26] BAHAADINI R, SAIDI A R. Stability analysis of thin-walled spinning reinforced pipes conveying fluid in thermal environment[J]. European Journal of Mechanics A: Solids, 2018, 72: 298-309. doi: 10.1016/j.euromechsol.2018.05.015 [27] PEI Y C, SUN Y H, WANG J X. Dynamics of rotating conveying mud drill string subjected to torque and longitudinal thrust[J]. Meccanica, 2013, 48(9): 2189-2201. doi: 10.1007/s11012-013-9733-8 [28] MA G H, SHEN X Q. Eigensolution of a bta deep-hole drilling shaft system[J]. Journal of Mechanical Science and Technology, 2018, 32(4): 1499-1504. doi: 10.1007/s12206-018-0303-9 [29] PANUSSIS D A, DIMAROGONAS A D. Linear in-plane and out-of-plane lateral vibrations of a horizontally rotating fluid-tube cantilever[J]. Journal of Fluids and Structures, 2000, 14(1): 1-24. doi: 10.1006/jfls.1999.0224 [30] YOON H I, SON I S. Dynamic response of rotating flexible cantilever pipe conveying fluid with tip mass[J]. International Journal of Mechanical Sciences, 2007, 49(7): 878-887. doi: 10.1016/j.ijmecsci.2006.11.006 [31] WANG L H, ZHONG Z. Dynamics of the dragonfly wings raised by blood circulation[J]. Acta Mechanica, 2014, 225(4/5): 1471-1485. [32] CHIU Y J, CHEN D Z. The coupled vibration in a rotating multi-disk rotor system[J]. International Journal of Mechanical Sciences, 2011, 53(1): 1-10. doi: 10.1016/j.ijmecsci.2010.10.001 [33] YOO H H, SHIN S H. Vibration analysis of rotating cantilever beams[J]. Journal of Sound and Vibration, 1998, 212(5): 807-828. doi: 10.1006/jsvi.1997.1469 -




 下载:
下载:


 渝公网安备50010802005915号
渝公网安备50010802005915号