Oldroyd-B流体绕拉伸楔形体的非稳态滑移流动与传热分析

白羽; 方慧灵; 张艳

doi:10.21656/1000-0887.420197

Oldroyd-B流体绕拉伸楔形体的非稳态滑移流动与传热分析

doi: 10.21656/1000-0887.420197

白羽^{1, 2, ,},
方慧灵^{1, 2,},
张艳^{1, 2,}

1.
北京建筑大学理学院，北京 102616
2.
建筑结构与环境修复功能材料北京市重点实验室，北京 102616

基金项目: 国家自然科学基金(21878018)；北京市自然科学基金和北京市教育委员会联合资助项目(KZ201810016018)

详细信息

作者简介:
白羽（1979—），女，副教授，博士，硕士生导师（通讯作者. E-mail：baiyu@bucea.edu.cn）

方慧灵（1997—），女，硕士生（E-mail：Niki9731@163.com）

张艳（1972—），女，教授，博士，硕士生导师（E-mail：zhangyan1@bucea.edu.cn）

中图分类号: O357
计量
- 文章访问数: 738
- HTML全文浏览量: 277
- PDF下载量: 45
- 被引次数: 0
出版历程
- 收稿日期: 2021-07-12
- 录用日期: 2021-07-12
- 修回日期: 2021-09-26
- 网络出版日期: 2022-01-28
- 刊出日期: 2022-03-08

Unsteady Slip Flow and Heat Transfer Analysis of Oldroyd-B Fluid Over the Stretching Wedge

BAI Yu^{1, 2
, ,},
FANG Huiling^{1, 2
,},
ZHANG Yan^{1, 2
,}

1.
School of Science, Beijing University of Civil Engineering and Architecture, Beijing 102616, P.R.China
2.
Beijing Key Laboratory of Functional Materials for Building Structure and Environment Remediation, Beijing 102616, P.R.China

摘要

摘要:
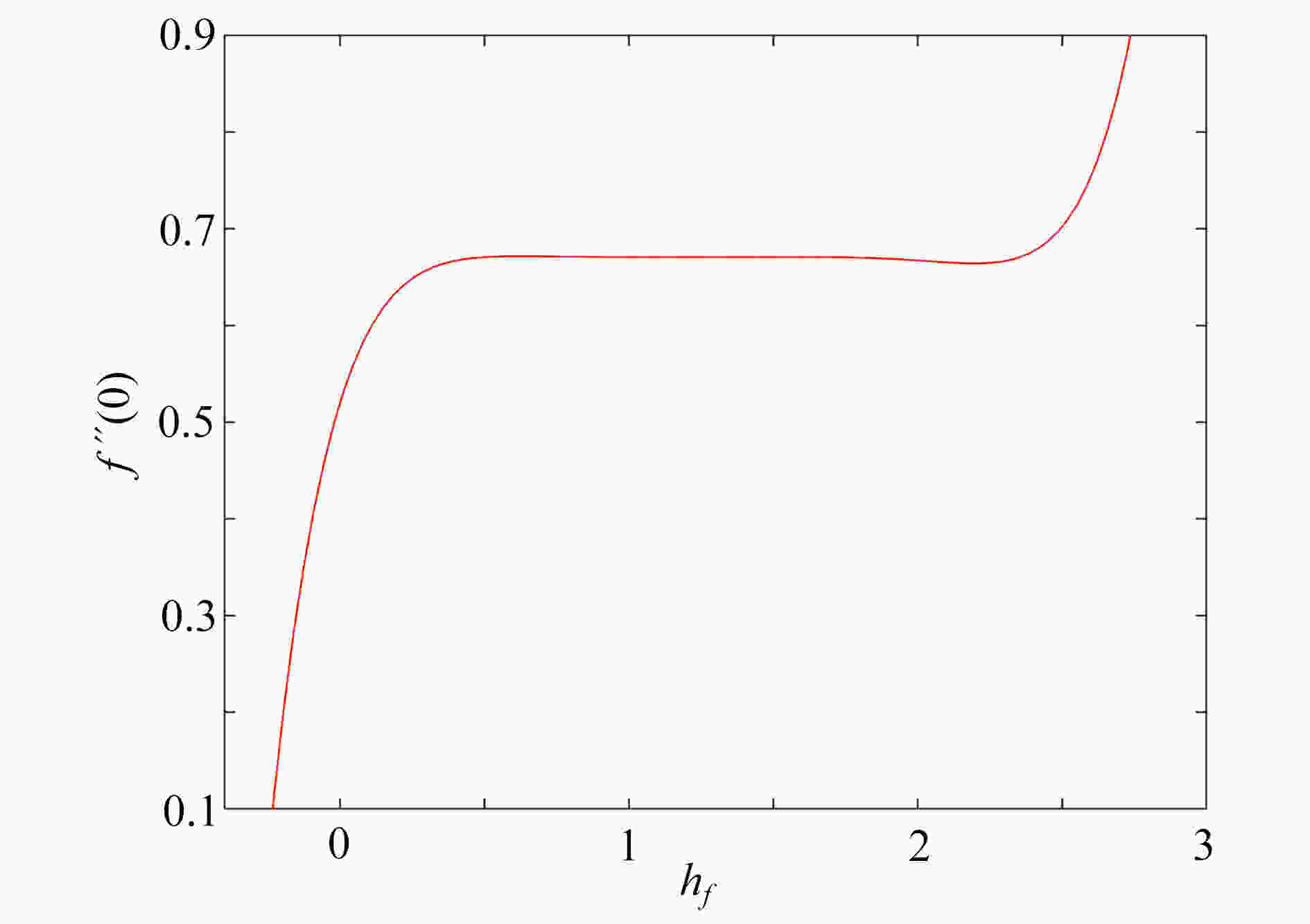
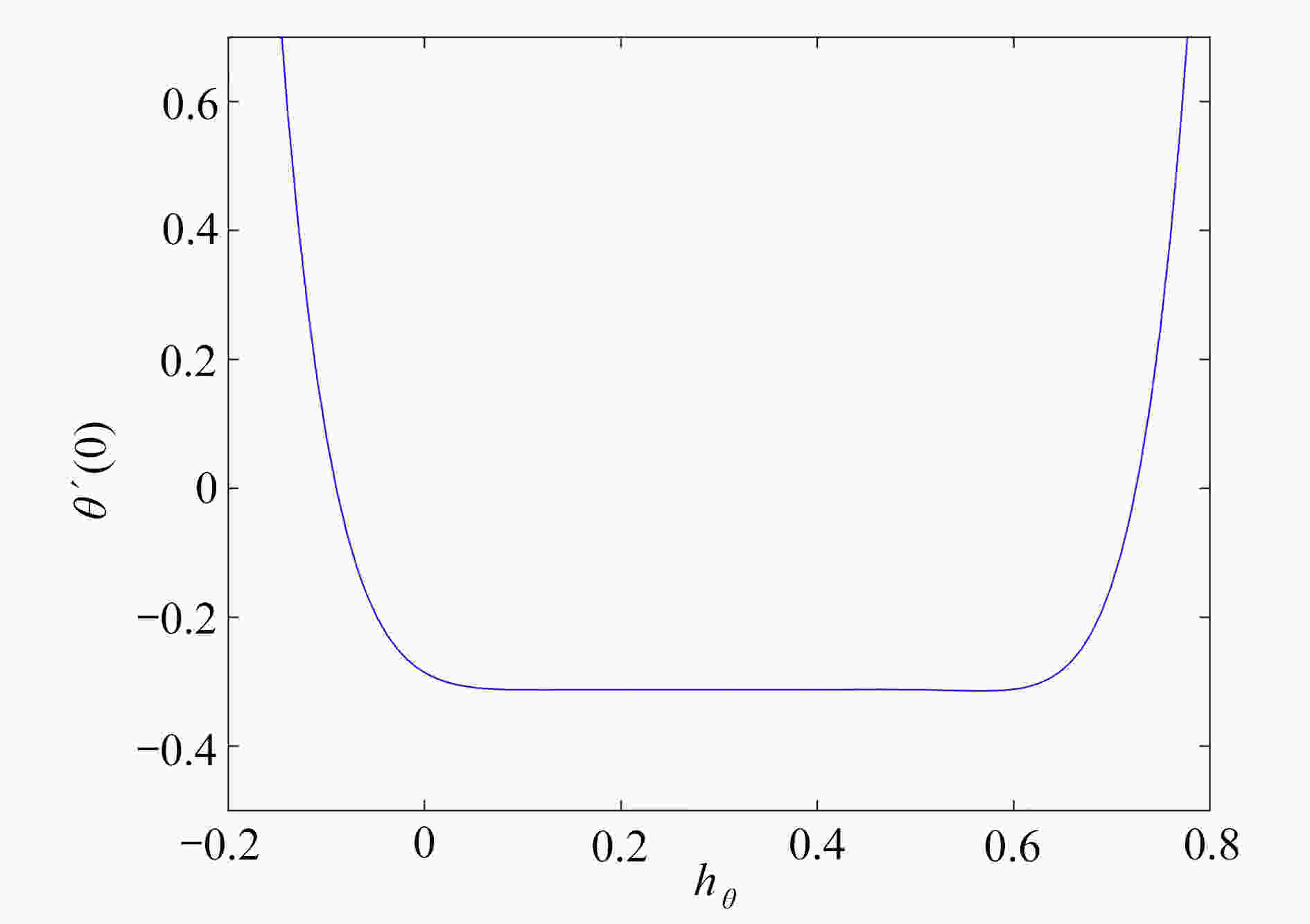
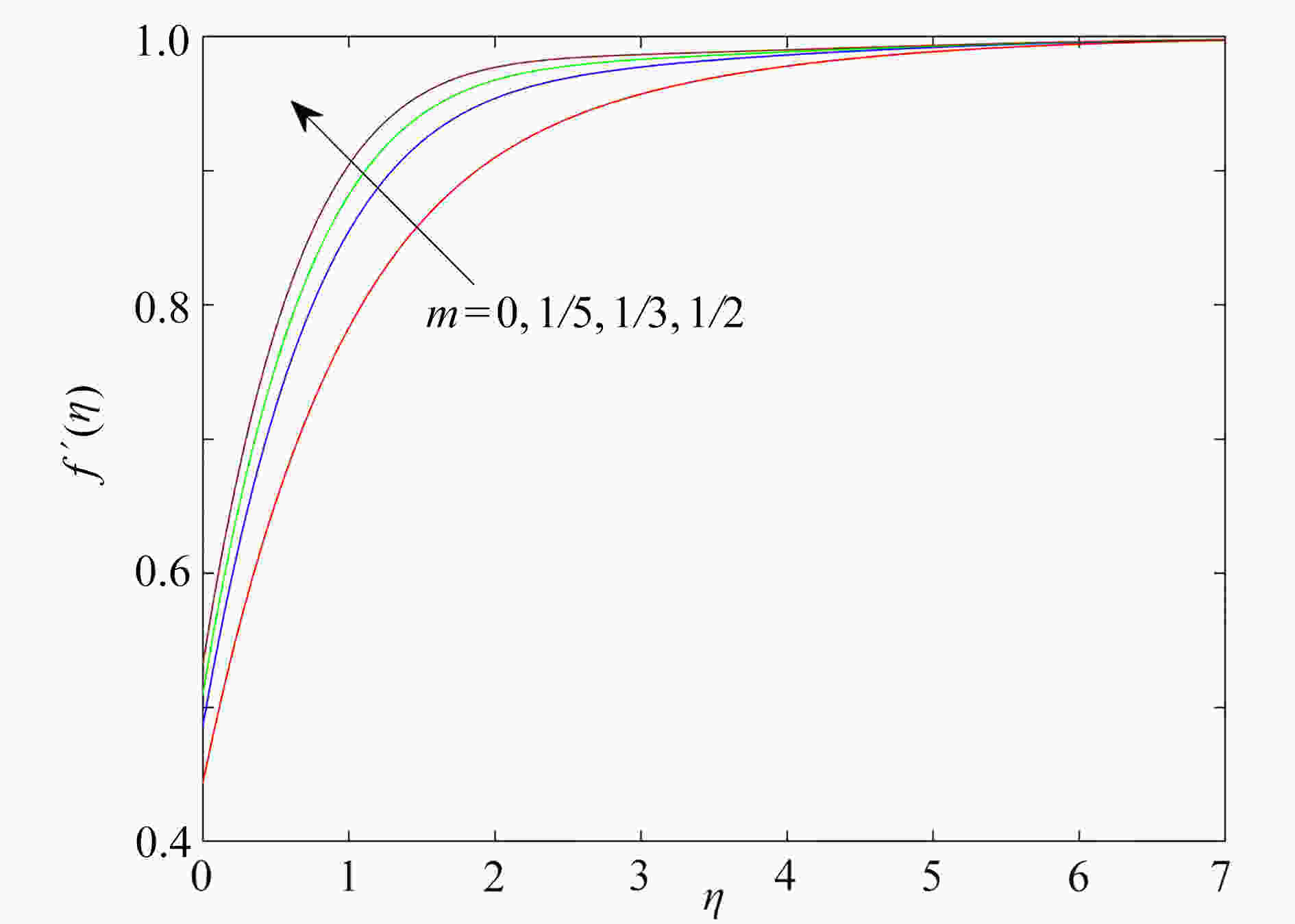
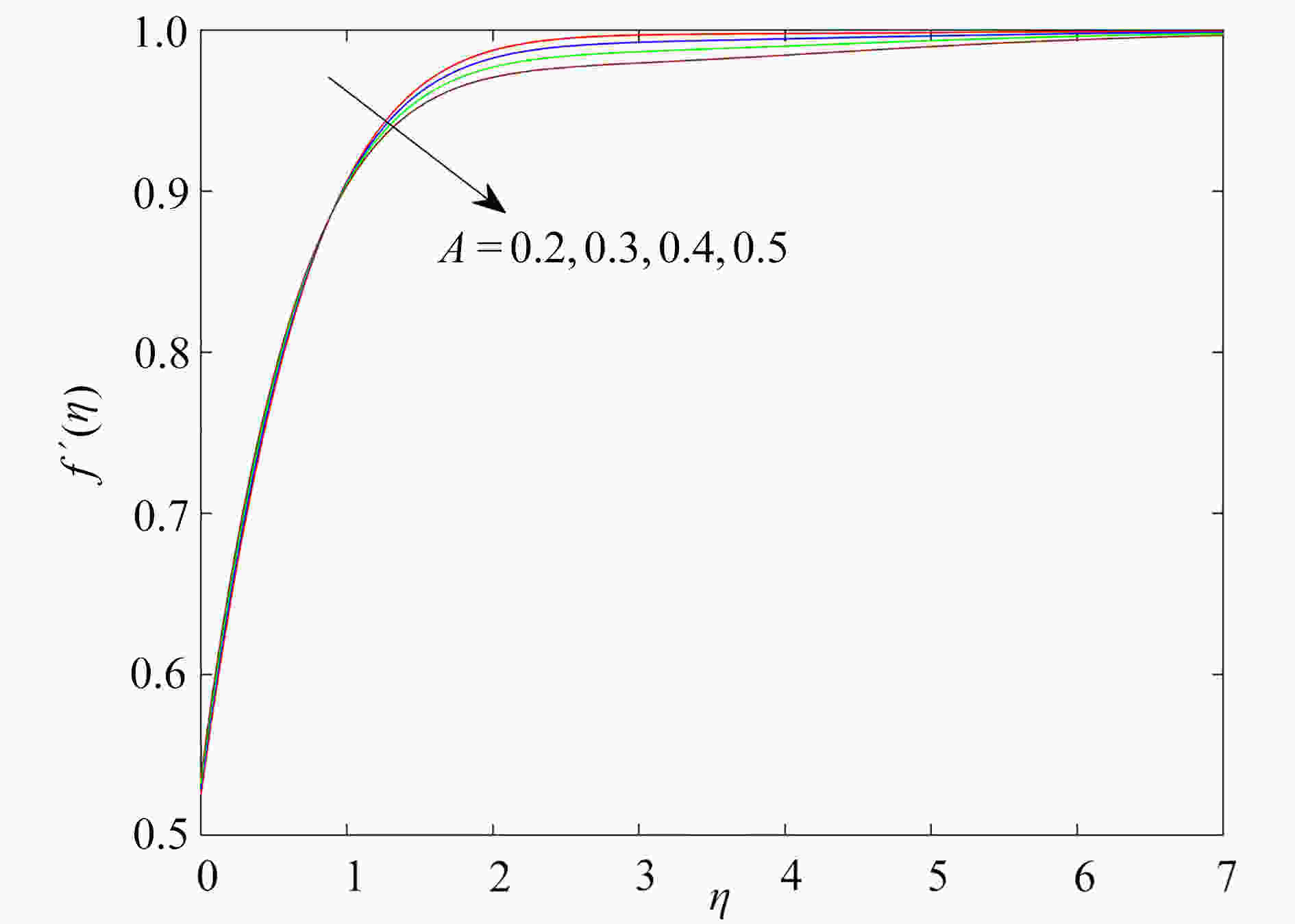
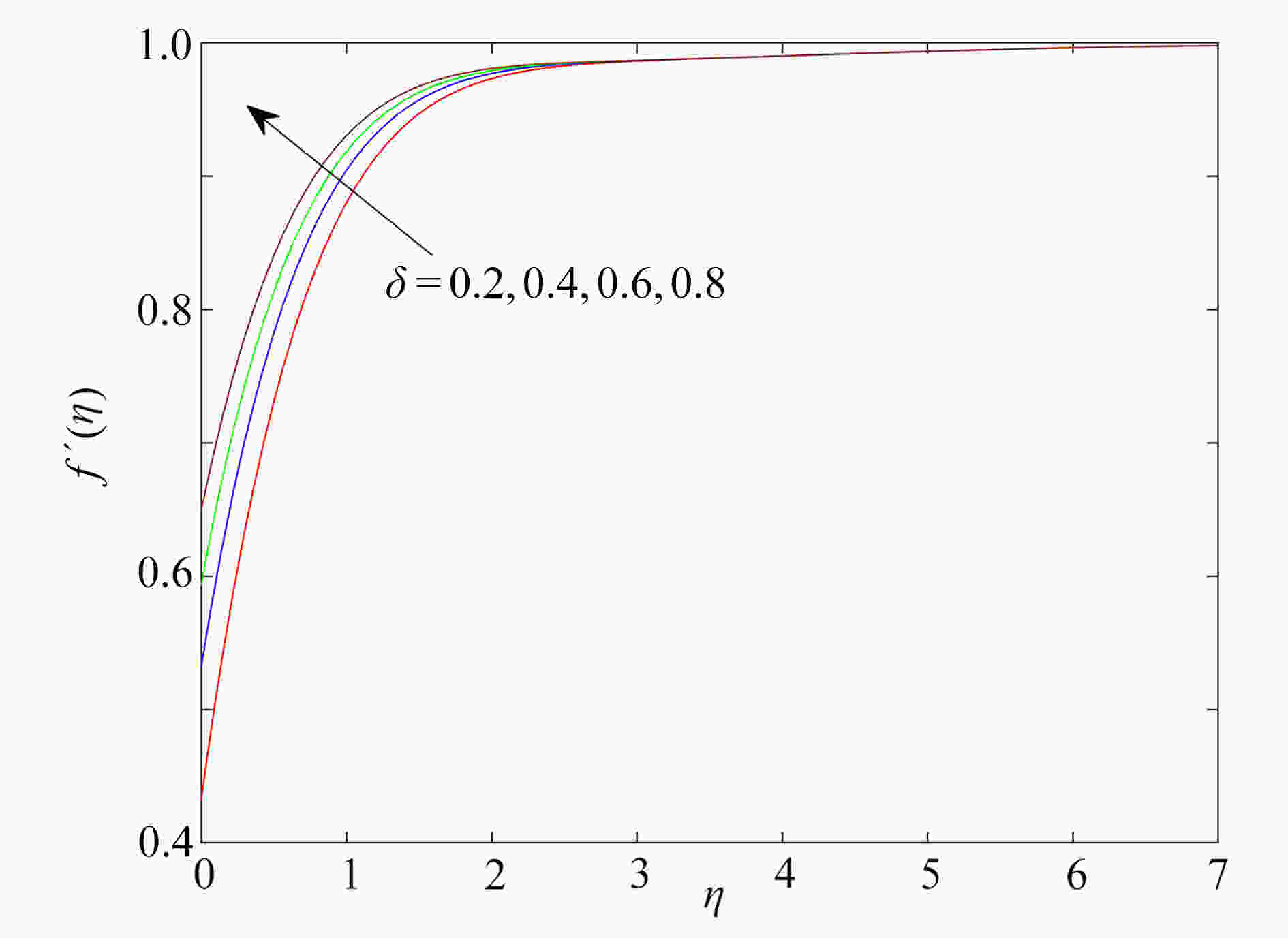
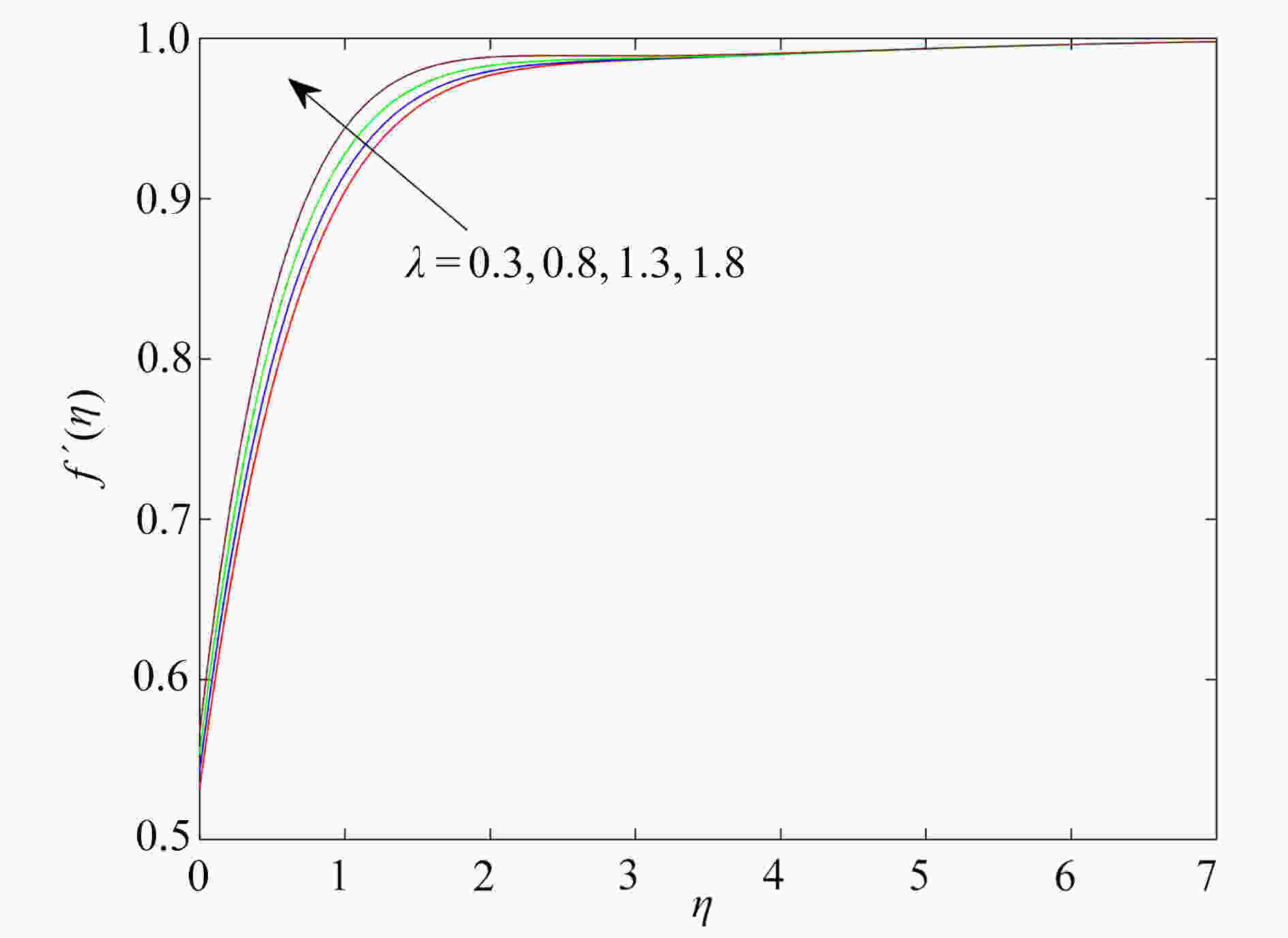
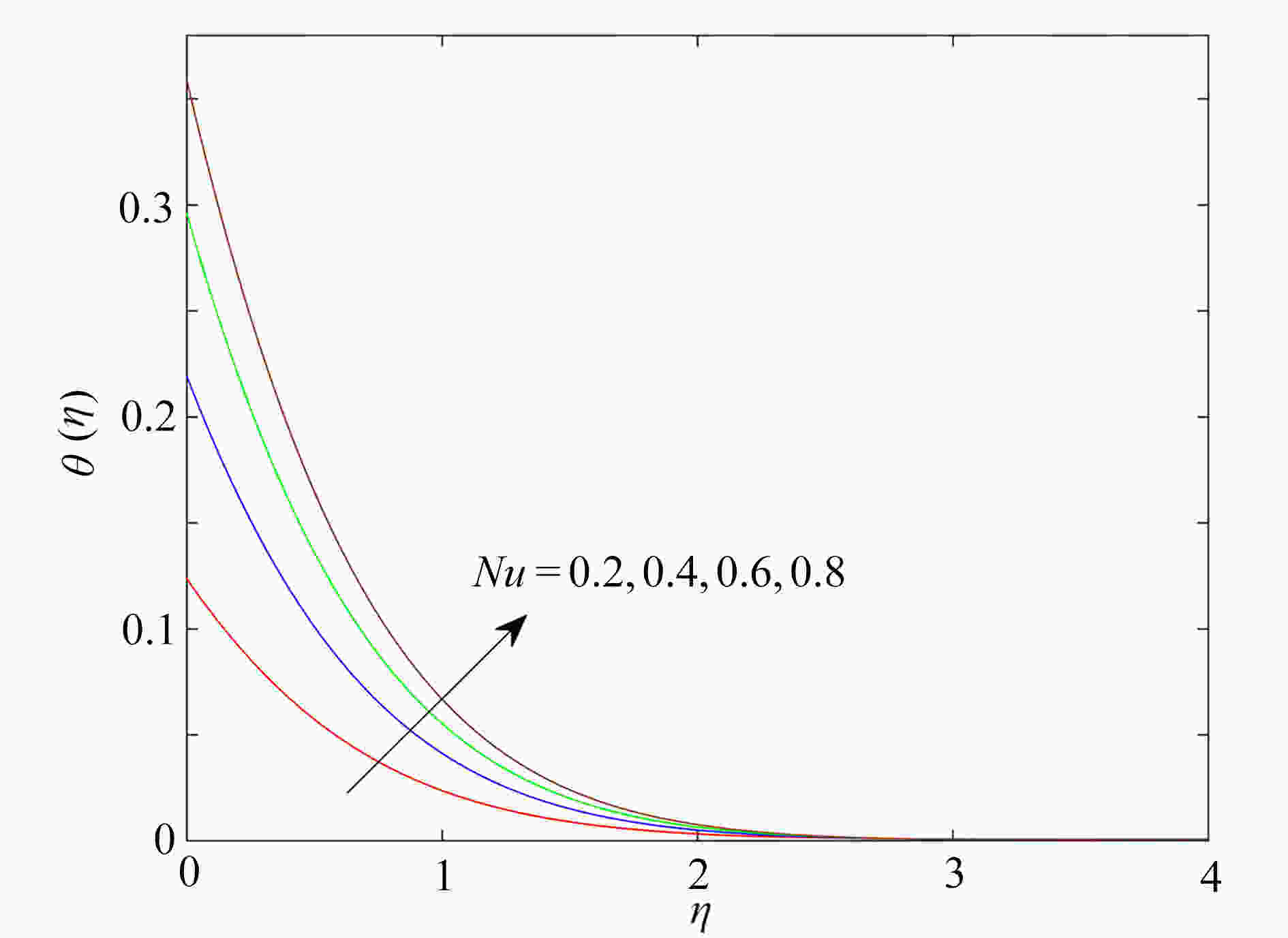
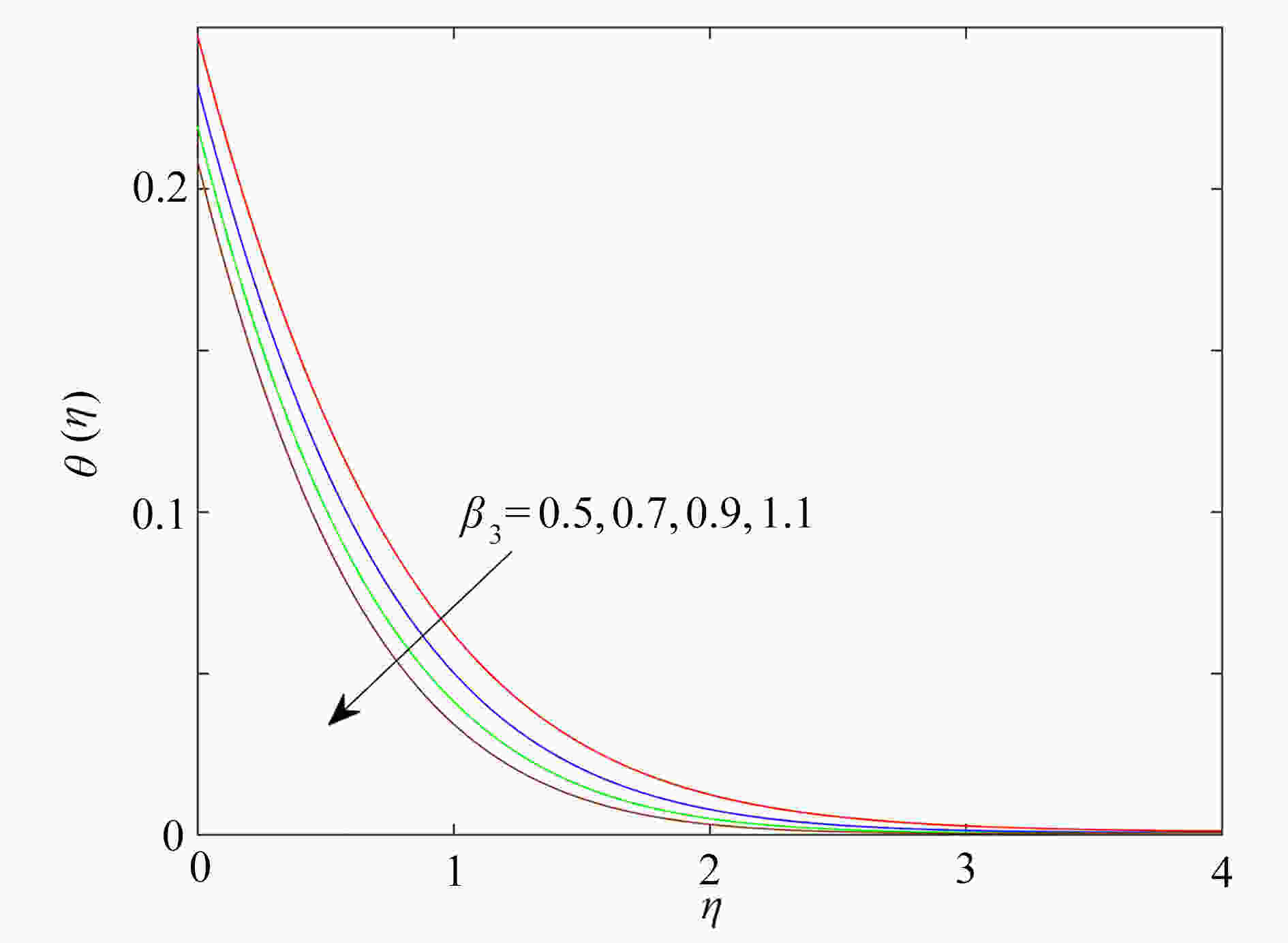
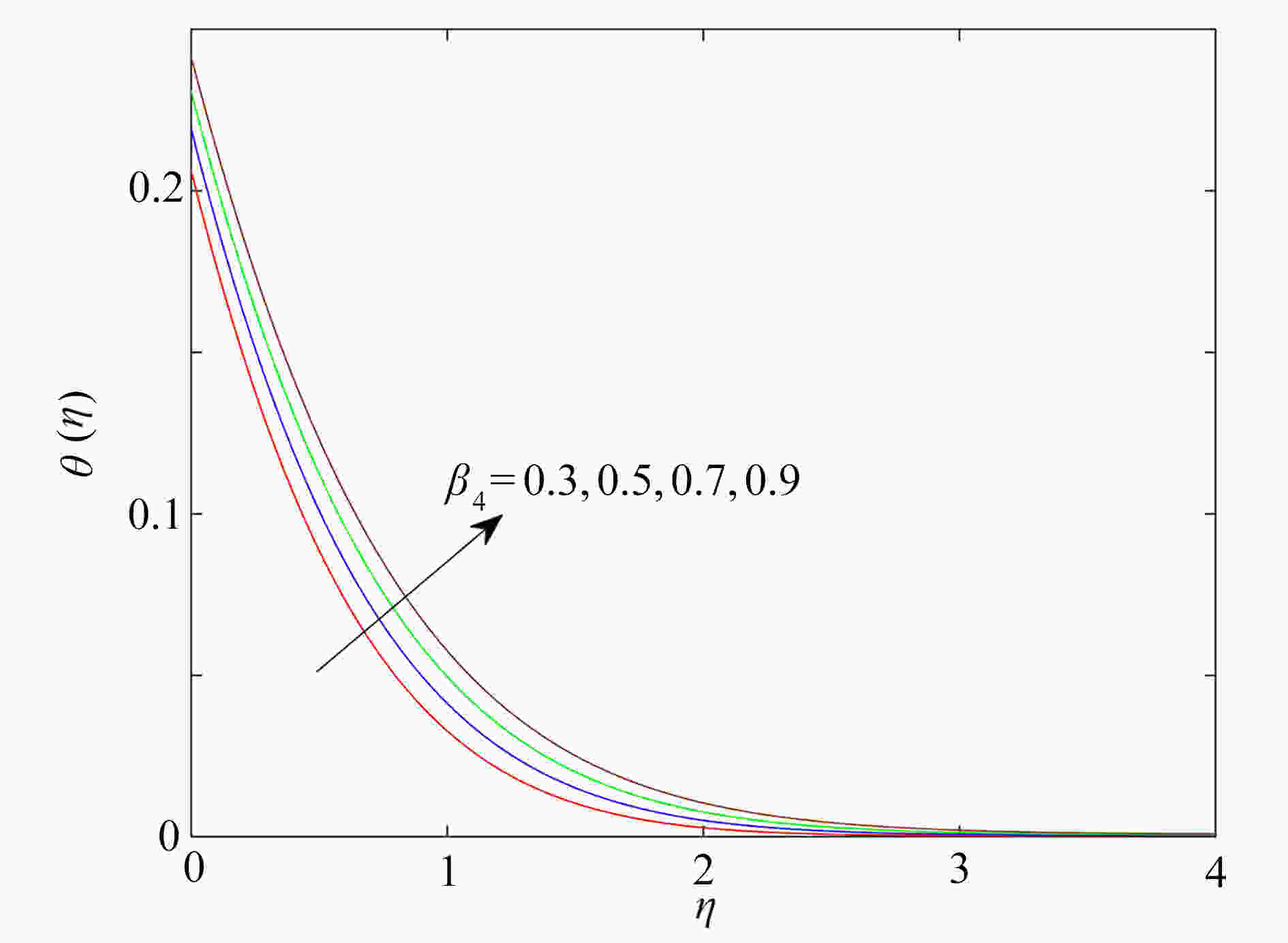
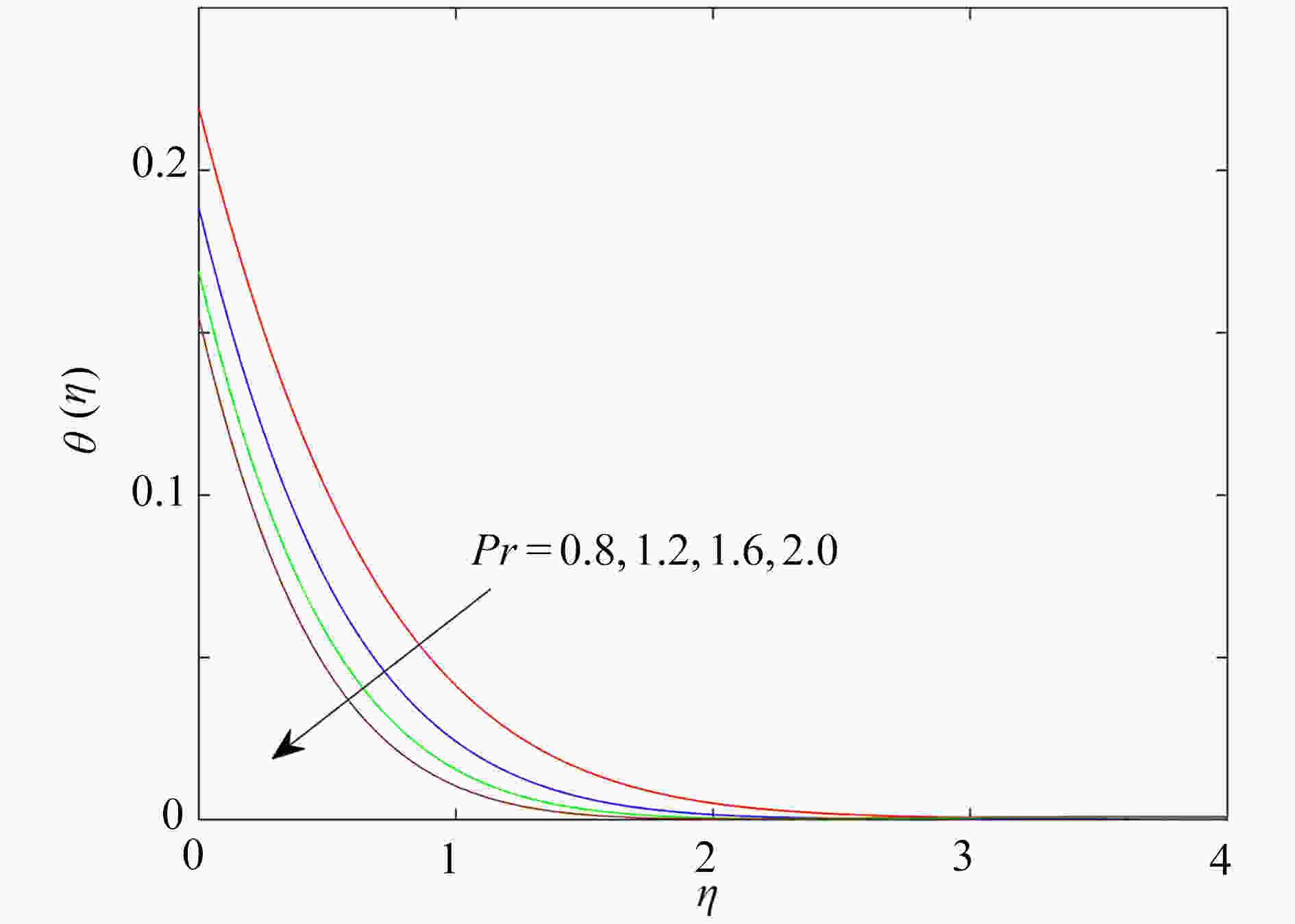
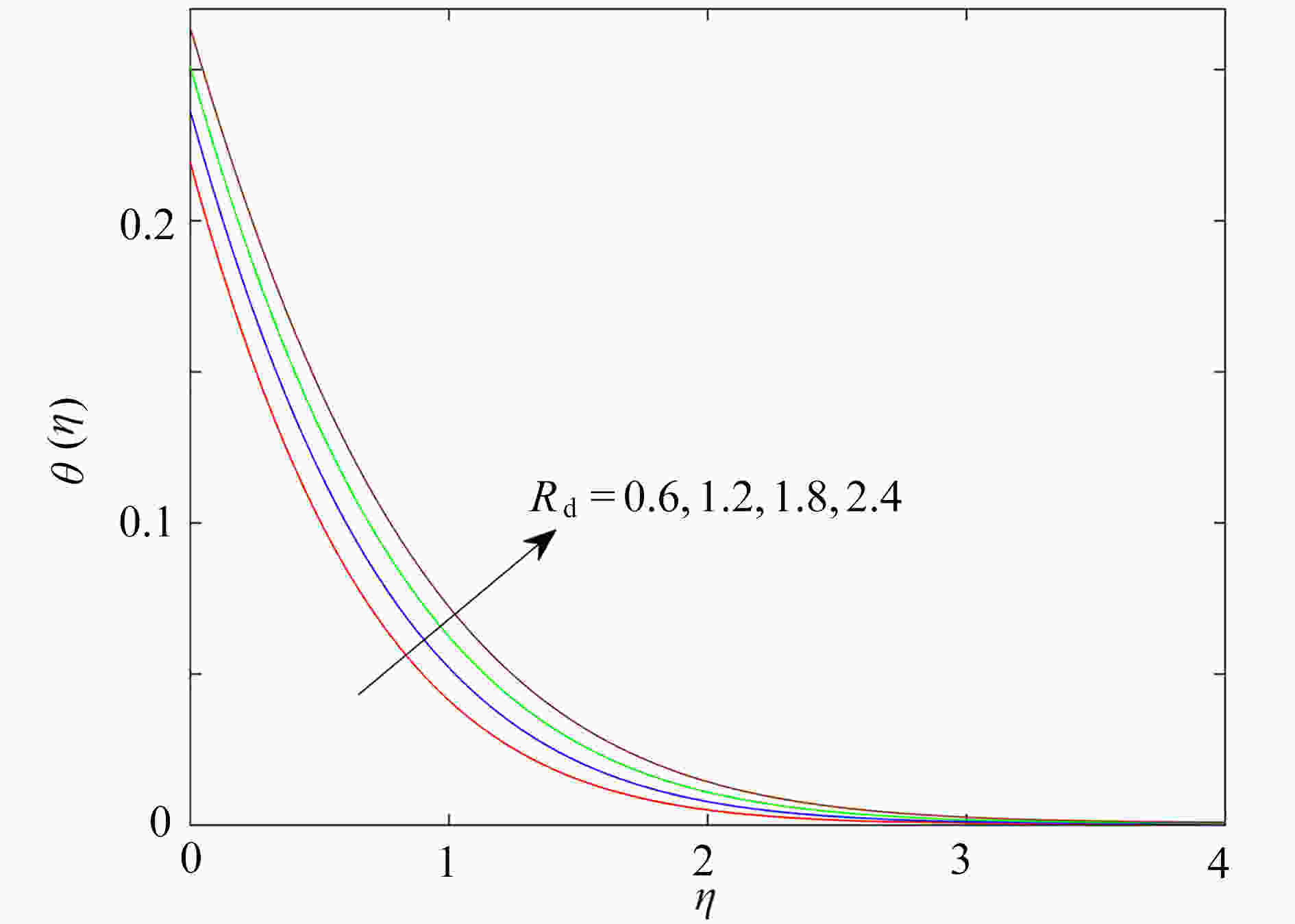
研究了在速度滑移现象存在下，上随体Oldroyd-B流体绕加热的楔形体的非稳态流动。采用松弛-延迟热通量模型，模拟了传热过程和热延迟时间对传热的影响，通过考虑浮升力、热辐射和对流换热边界条件，进一步研究了流动及传热特性。利用同伦分析方法获得常微分方程组的近似解析解，发现滑移参数的增大可以促进流体的流动，以及流体的温度随热辐射参数增大而升高。此外还发现，温度场在热松弛时间和热延迟时间中出现相反的变化趋势。
- Oldroyd-B流体 /
- 楔形体 /
- 非稳态流动 /
- 速度滑移 /
- 热辐射 /
- 松弛-延迟热通量模型
Abstract:
The unsteady flow of the upper-convected Oldroyd-B fluid over the heated wedge in the presence of velocity slip was discussed. The process of heat transfer and the effect of the thermal retardation time on heat transfer were simulated with the relaxation-retardation heat flux model. The buoyancy, the thermal radiation and the convective heat transfer boundary condition were considered to further elucidate the flow and heat transfer characteristics. The homotopy analysis method was used to obtain the approximate analytical solutions to ordinary differential equations. It is found that the magnification of the slip parameter can promote the flow of fluid, and the fluid temperature rises with the thermal radiation parameter. In addition, the temperature field shows opposite trends in the thermal relaxation time and the thermal retardation time.
- Oldroyd-B fluid /
- wedge /
- unsteady flow /
- velocity slip /
- thermal radiation /
- relaxation-retardation heat flux model

HTML全文

图 1 物理模型示意图

Figure 1. Schematic diagram of the physical model

下载: 全尺寸图片幻灯片

图 2 h_f-f"(0)曲线图

Figure 2. The h_f-f"(0) curve

下载: 全尺寸图片幻灯片

图 3 h_θ-θ'(0)曲线图

Figure 3. The h_θ-θ'(0) curve

下载: 全尺寸图片幻灯片

图 4 不同m下的速度分布

Figure 4. Velocity distributions for different m values

下载: 全尺寸图片幻灯片

图 5 不同A下的速度分布

Figure 5. Velocity distributions for different A values

下载: 全尺寸图片幻灯片

图 6 不同δ下的速度分布

Figure 6. Velocity distributions for different δ values

下载: 全尺寸图片幻灯片

图 7 不同β₂下的速度分布

Figure 7. Velocity distributions for different β₂values

下载: 全尺寸图片幻灯片

图 8 不同λ下的速度分布

Figure 8. Velocity distributions for different λ values

下载: 全尺寸图片幻灯片

图 9 不同Nu下的温度分布

Figure 9. Temperature distributions for different Nu values

下载: 全尺寸图片幻灯片

图 10 不同β₃下的温度分布

Figure 10. Temperature distributions for different β₃values

下载: 全尺寸图片幻灯片

图 11 不同β₄下的温度分布

Figure 11. Temperature distributions for different β₄values

下载: 全尺寸图片幻灯片

图 12 不同Pr下的温度分布

Figure 12. Temperature distributions for different Pr values

下载: 全尺寸图片幻灯片

图 13 不同R_d下的温度分布

Figure 13. Temperature distributions for different R_dvalues

下载: 全尺寸图片幻灯片

表 1 同伦解f"(0)与文献[4]结果的比较

Table 1. Comparison of the values of f"(0) with the results of ref. [4]

m 0 1/5 1/3

ref. [4] 0.469 6 0.802 1 0.927 7
present result 0.469 6 0.802 1 0.927 7

下载: 导出CSV

参考文献(18)

[1]	FALKNER V M, SKAN S W. Solutions of the boundary-layer equations[J]. Philosophical Magazine, 1931, 12(80): 865-896.
[2]	LIN H T, LIN L K. Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any Prandtl number[J]. International Journal of Heat and Mass Transfer, 1987, 30(6): 1111-1118. doi: 10.1016/0017-9310(87)90041-X
[3]	KUO B L. Heat transfer analysis for the Falkner-Skan wedge flow by the differential transformation method[J]. International Journal of Heat and Mass Transfer, 2005, 48(23/24): 5036-5046.
[4]	AFIFY A A, BAZID M A A. MHD Falkner-Skan flow and heat transfer characteristics of nanofluids over a wedge with heat source/sink effects[J]. Journal of Computational and Theoretical Nanoscience, 2014, 11(8): 1844-1852. doi: 10.1166/jctn.2014.3578
[5]	ASHRAF M B, HAYAT T, ALSULAMI H. Mixed convection Falkner-Skan wedge flow of an Oldroyd-B fluid in presence of thermal radiation[J]. Journal of Applied Fluid Mechanic, 2016, 9: 1753-1762. doi: 10.18869/acadpub.jafm.68.235.24323
[6]	MAHDY A, CHAMKHA A J. Unsteady MHD boundary layer flow of tangent hyperbolic two-phase nanofluid of moving stretched porous wedge[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2018, 28(11): 2567-2580.
[7]	KEBEDE T, HAILE E, AWGICHEW G, et al. Heat and mass transfer analysis in unsteady flow of tangent hyperbolic nanofluid over a moving wedge with buoyancy and dissipation effects[J]. Heliyon, 2020, 6(4): e03776. doi: 10.1016/j.heliyon.2020.e03776
[8]	朱婧, 郑连存, 张志刚. 幂律速度运动表面上磁流体在驻点附近的滑移流动[J]. 应用数学和力学, 2010, 31(4): 411-419. (ZHU Jing, ZHENG Liancun, ZAHNG Zhigang. Efect of the slip condition on the MHD stagnation-point flow over a power-law stretching sheet[J]. Applied Mathematics and Mechanics, 2010, 31(4): 411-419.(in Chinese) doi: 10.3879/j.issn.1000-0887.2010.04.004
[9]	ZHU J, YANG D, ZHENG L C, et al. Effects of second order velocity slip and nanoparticles migration on flow of Buongiorno nanofluid[J]. Applied Mathematics Letters, 2016, 52: 183-191. doi: 10.1016/j.aml.2015.09.003
[10]	许晓勤, 陈淑梅. 基于二阶滑移边界的MHD 在可渗透延伸壁面上的驻点流研究[J]. 应用数学和力学, 2016, 37(8): 880-888. (XU Xiaoqin, CHEN Shumei. Study on MHD stagnation-point flow over permeable stretching sheets with 2nd-order slip boundaries[J]. Applied Mathematics and Mechanics, 2016, 37(8): 880-888.(in Chinese)
[11]	MEGAHED A M. Improvement of heat transfer mechanism through a Maxwell fluid flow over a stretching sheet embedded in a porous medium and convectively heated[J]. Mathematics and Computers in Simulation, 2021, 187: 97-109. doi: 10.1016/j.matcom.2021.02.018
[12]	CATTANEO C. Sulla conduzione del calore[J]. Atti del Seminario Matematico e Fisico Dell’Universita di Modena e Reggio Emilia, 1948, 3: 83-101.
[13]	CHRISTOV C I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction[J]. Mechanics Research Communications, 2009, 36(4): 481-486. doi: 10.1016/j.mechrescom.2008.11.003
[14]	HAYAT T, AYUB T, MUHAMMAD T. Flow of variable thermal conductivity Oldroyd-B fluid with generalized Fourier’s and Fick’s laws[J]. Journal of Molecular Liquilds, 2017, 234: 9-17. doi: 10.1016/j.molliq.2017.03.053
[15]	SHEHZAD S A, ABBASI F M, HAYAT T, et al. Cattaneo-Christov heat flux model for Darcy-Forchheimer flow of an Oldroyd-B fluid with variable conductivity and non-linear convection[J]. Journal of Molecular Liquilds, 2016, 224: 274-278. doi: 10.1016/j.molliq.2016.09.109
[16]	ZHANG Y, BAI Y, YUAN B, et al. Flow and heat transfer analysis of a Maxwell-power-law fluid film with forced thermal Marangoni convective[J]. Internatinal Communications in Heat and Mass Transfer, 2021, 121: 105062. doi: 10.1016/j.icheatmasstransfer.2020.105062
[17]	BAI Y, WANG Q, ZHANG Y. Unsteady stagnation-point flow of upper-convected Oldroyd-B nanofluid with variable thermal conductivity and relaxation-retardation double-diffusion model[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2021, 31(11): 3373-3393.
[18]	LIAO S. Beyond perturbation: introduction to the homotopy analysis method[J]. Applied Mechanics Reviews, 2003, 57(5): B25-B26.

施引文献

资源附件(0)

访问统计

图(13) / 表(1)

计量

文章访问数: 738
HTML全文浏览量: 277
PDF下载量: 45
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

Oldroyd-B流体绕拉伸楔形体的非稳态滑移流动与传热分析

doi: 10.21656/1000-0887.420197

作者简介:
白羽（1979—），女，副教授，博士，硕士生导师（通讯作者. E-mail：baiyu@bucea.edu.cn）

方慧灵（1997—），女，硕士生（E-mail：Niki9731@163.com）

张艳（1972—），女，教授，博士，硕士生导师（E-mail：zhangyan1@bucea.edu.cn）

计量

Unsteady Slip Flow and Heat Transfer Analysis of Oldroyd-B Fluid Over the Stretching Wedge

计量

目录

m	0	1/5	1/3
ref. [4]	0.469 6	0.802 1	0.927 7
present result	0.469 6	0.802 1	0.927 7

留言板

Oldroyd-B流体绕拉伸楔形体的非稳态滑移流动与传热分析

doi: 10.21656/1000-0887.420197

作者简介: 白羽（1979—），女，副教授，博士，硕士生导师 （通讯作者. E-mail：baiyu@bucea.edu.cn） 方慧灵（1997—），女，硕士生（E-mail：Niki9731@163.com） 张艳（1972—），女，教授，博士，硕士生导师（E-mail：zhangyan1@bucea.edu.cn）

计量

出版历程

Unsteady Slip Flow and Heat Transfer Analysis of Oldroyd-B Fluid Over the Stretching Wedge

计量

出版历程

目录

作者简介:
白羽（1979—），女，副教授，博士，硕士生导师（通讯作者. E-mail：baiyu@bucea.edu.cn）

方慧灵（1997—），女，硕士生（E-mail：Niki9731@163.com）

张艳（1972—），女，教授，博士，硕士生导师（E-mail：zhangyan1@bucea.edu.cn）