Dynamic Changes of Influenza A/H1N1 Epidemic Evaluated Based on the Kolmogorov Forward Equation
-
摘要:
基于个体水平的传染病模型可以揭示随机性在传染病疫情防控中的重要作用。研究此类模型的普遍方法是通过事件驱动的、大量重复的随机模拟来确定预测变量的范围。而基于Kolmogorov前向方程(KFE)研究个体水平的传染病模型,不仅不需要大量的重复模拟来确定预测变量的范围,而且可以同时考虑每种状态发生的概率。因此,基于2009年西安市第八医院甲型H1N1流感数据,建立了基于社交网络的个体决策心理模型,以确定行为改变率;进一步地,为得到传染病传播过程中各状态的概率分布,基于改进的个体SIR模型,通过Markov过程推导出KFE。结果表明:通过数值求解KFE可以得到整个爆发过程中每种状态发生的概率分布、最严重的时间段及相应的概率,从而能更快、更准确地了解甲型H1N1疫情的传播过程,因此有助于高效地进行甲型H1N1疫情防控。
-
关键词:
- 甲型H1N1 /
- Markov过程 /
- Kolmogorov前向方程(KFE) /
- 隐式Euler (IE)法 /
- 最终规模
Abstract:The individual-based infectious disease models show the important role of stochasticity in infectious disease prevention and control. To study these models and then determine the ranges of predictive variables, an increasingly common approach needs event-driven massive repetitive stochastic simulations. The study of the individual-based infectious disease models based on the Kolmogorov forward equation (KFE), not only could overcome the difficulty of repeated simulations, but could consider the probability of each state simultaneously. Therefore, according to the data of 2009 influenza A/H1N1 in the Xi’an 8th Hospital, to determine the rate of behavior change, an individual decision-making psychological model was established based on social network. Further, in order to obtain the probability distribution of each state in the process of infectious disease transmission, based on the modified individual SIR model, the KFE was derived through the Markov processes. The results show that, the numerical solution of the KFE gives the probability distribution of each state, the most serious period and the corresponding probability in the outbreak process of epidemic infectious diseases, so as to help understand the transmission process of A/H1N1 epidemic more quickly and accurately, which is valuable for the efficient prevention and control of A/H1N1 epidemic.
-
Key words:
- A/H1N1 /
- Markov process /
- Kolmogorov forward equation (KFE) /
- implicit Euler (IE) method /
- final size
-
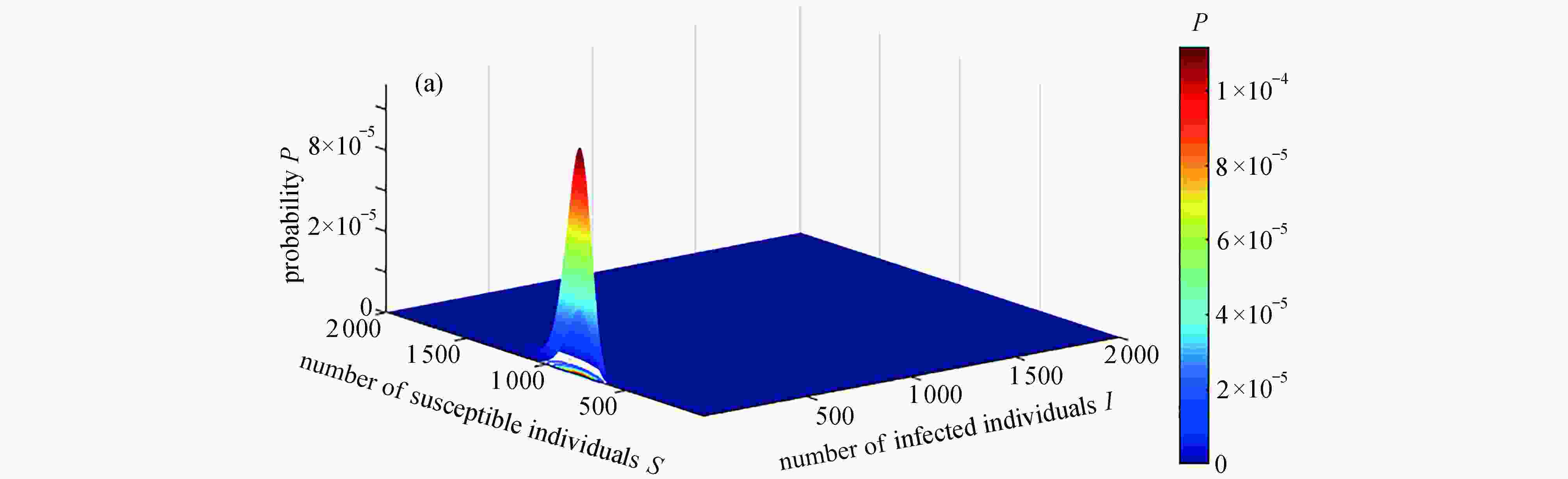
2 流感流行38天计算出的概率质量函数的快照: (a)到第38天时,感染人数与易感人数的联合条件概率质量函数
$ P(S(t),I(t)|I(t)>0) $ ;(b)概率质量函数的轮廓图;(c)第38天恢复人数的条件概率质量函数$ P(R(t)|I(t)>0) $ 2. A snapshot of the calculated probability mass function at the end of the 38 d influenza epidemic: (a)joint conditional probability mass function
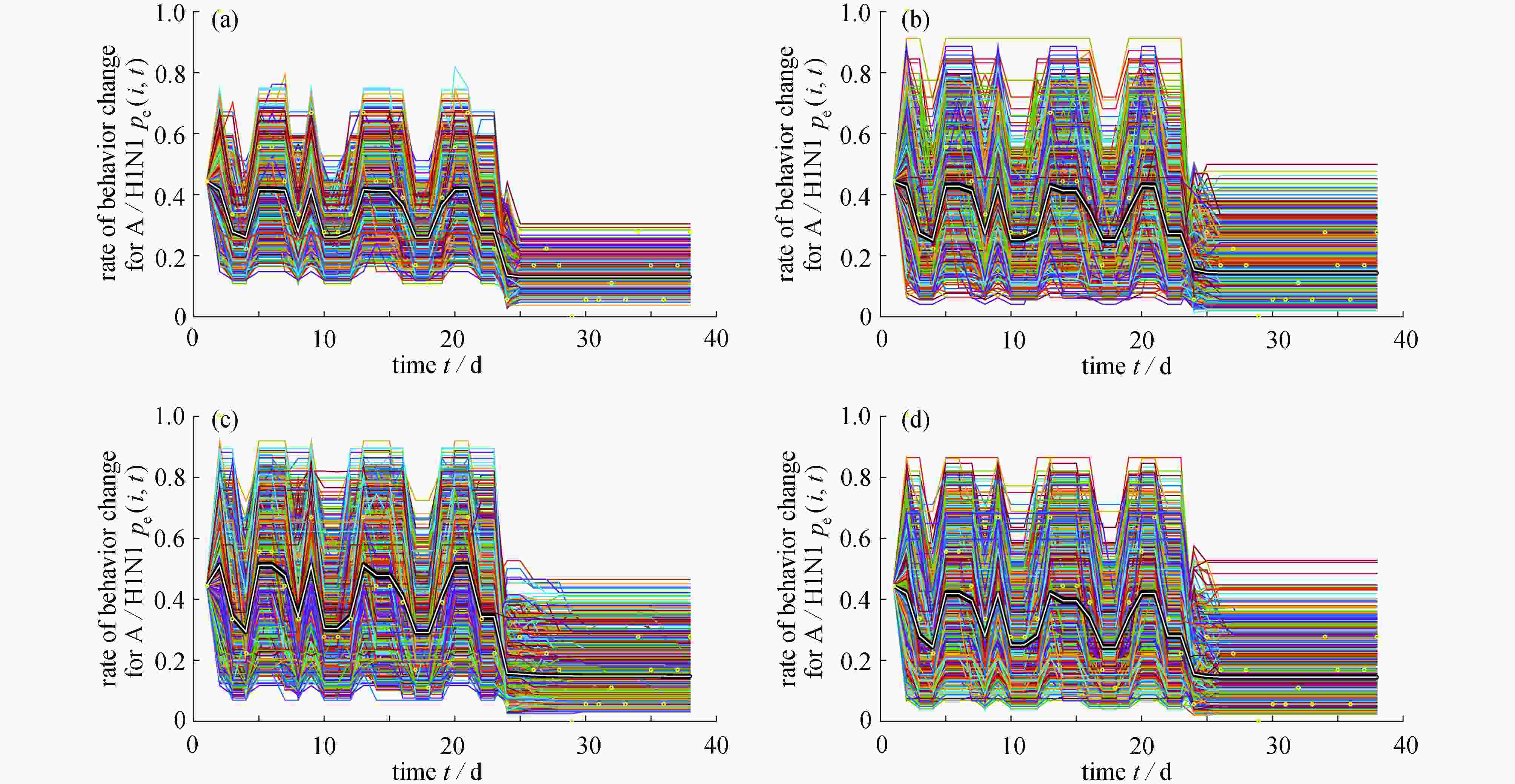
$ P(S(t),I(t)|I(t)>0) $ of infected and susceptible individuals; (b) the contour of the calculated probability mass function; (c) conditional probability mass function$ P(R(t)|I(t)>0) $ of recovered individualsA2 基于模型(A6),对2 004个个体的个体行为改变率
$ p_{{\rm{e}}}(i,t) $ 进行估计: (a)规则网络; (b) 小世界(WS) 网络; (c)NW 网络; (d) 随机网络A2. The estimation of individual behaviour change rate
$ p_{e}(i,t) $ for 2 004 persons based on model (A6): (a) the regular network; (b) the small-world (WS) network; (c) the Newman and Watts (NW) network; (d) the random networkA1 在四种经典的社交网络结构下, 模型(A6)所有参数均值和标准差的估计值及取值范围
A1. The estimated values and ranges of means and standard deviations for all parameters of model (A6) with 4 classical social networks
mean $ \mu $ min max best fit (regular) best fit (WS) best fit (NW) best fit (random) $ \delta $ 0.35 0.58 0.410 7 0.475 1 0.580 0 0.475 0 $ \lambda $ 170 195 175.116 8 175.402 1 174.625 0 173.485 0 $ \tau $ 6 8 6.761 4 6.898 6 6.895 5 6.510 9 $ \xi $ 10 50 18.781 0 21.449 0 20.966 4 10.047 5 $ \eta $ 0.3 0.6 0.599 5 0.482 2 0.513 3 0.414 5 $ O_0 $ −0.75 −0.6 −0.637 3 −0.710 2 −0.613 6 −0.631 7 $O_{ {1} }$ 0.001 0.1 0.009 3 0.060 8 0.059 0 0.048 4 $O_{2}$ 0.65 1 0.717 0 0.846 3 0.999 3 0.759 6 $O_3$ 0.01 0.15 0.065 4 0.092 3 0.149 8 0.084 0 $O_4$ −0.75 −0.45 −0.504 5 −0.579 9 −0.497 2 −0.520 9 standard deviation $ \sigma $ min max best fit (regular) best fit (WS) best fit (NW) best fit (random) $ \delta $ 0.01 0.1 0.038 1 0.058 3 0.094 0 0.046 7 $ \lambda $ 1 5 3.591 6 3.837 8 4.458 9 3.144 4 $ \tau $ 0 2 0.625 5 0.800 1 1.129 9 0.199 7 $ \xi $ 2 2 2.000 0 2.000 0 2.000 0 2.000 0 $ \eta $ 0.1 0.1 0.100 0 0.100 0 0.100 0 0.100 0 $ O_0 $ 0.2 0.6 0.293 9 0.388 3 0.210 9 0.396 7 $O_1$ 0.01 0.4 0.343 0 0.306 3 0.200 7 0.010 0 $O_2$ 0.3 0.5 0.316 3 0.409 3 0.427 8 0.342 1 $O_3$ 0.01 0.1 0.030 2 0.054 3 0.094 2 0.050 3 $O_4$ 0.1 0.5 0.100 4 0.406 1 0.499 0 0.141 7 -
[1] BARTLETT M S. Deterministic and stochastic models for recurrent epidemics[C]//Process Third Berkley Sympathetic Mathematical Statstics and Probalibity. 1956, 4(1956): 81-108. [2] RAND D A, WILSON H B. Chaotic stochasticity: a ubiquitous source of unpredictability in epidemics[J]. Proceedings of the Royal Society B, 1991, 246(1316): 179-184. [3] FOX G A. Life-history evolution and demographic stochasticity[J]. Ecology and Evolution, 1993, 7(1): 1-14. [4] GRENFELL B T, WILSON K, FINKENSTA B F, et al. Noise and determinism in synchronized sheep dynamics[J]. Nature, 1998, 394(6694): 674-677. [5] KEELING M J, WILSON H B, PACALA S W. Re-interpreting space time-lags and functional responses in ecological models[J]. Science, 2000, 290(5497): 1758-1761. [6] GILLESPIE D T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions[J]. Journal of Computational Physics, 1976, 22(4): 403-434. [7] RENSHAW E. Modelling Biological Populations in Space and Time[M]. Cambridge: Cambridge University Press, 1995. [8] VAN KAMPEN N G. Stochastic Processes in Physics and Chemistry[M]. Amsterdam: Noth-Holland, 1983. [9] JENKINSON G, GOUTSIAS J. Numerical integration of the master equation in some models of stochastic epidemiology[J]. PLoS ONE, 2012, 7(5): e36160. [10] KEELING M J, ROSS J V. On methods for studying stochastic disease dynamics[J]. Journal of Royal Society Interface, 2008, 5(19): 171-181. [11] DIECKMANN U, LAW R. The dynamical theory of coevolution: a derivation from stochastic ecological processes[J]. Journal of Mathematical Biology, 1996, 34(5/6): 579-612. [12] ALONSO D, MCKANE A. Extinction dynamics in mainland-island metapopulations: an N-patch stochastic model[J]. Bulletin of Mathematical Biology, 2002, 64(5): 913-958. [13] ALONSO D, MCKANE A J, PASCUAL M. Stochastic amplification in epidemics[J]. Journal of the Royal Society Interface, 2006, 4(14): 575-582. [14] VIET A, MEDLEY G F. Stochastic dynamics of immunity in small populations: a general framework[J]. Mathematical Biosciences, 2006, 200(1): 28-43. [15] POLETTI P, CAPRILE B, AJELLI M, et al. Spontaneous behavioural changes in response to epidemics[J]. Journal of Theoretical Biology 2009, 260(1): 31-40. [16] POLETTI P. Human behaviour in epidemic modelling[D]. PhD Thesis. Trento: University of Trento, 2010. [17] DURHAM D P, CASMAN E A. Incorporating individual health-protective decisions into disease transmission models: a mathematical framework[J]. Journal of Royal Society Interface, 2012, 9(68): 562-570. [18] YAN Q L, TANG S Y, XIAO Y N. Impact of individual behaviour change on the spread of emerging infectious diseases[J]. Statistics in Medicine, 2018, 37(6): 948-969. [19] VAN KAMPEN N G. Stochastic processes in physics and chemistry[J]. Physics Today, 1983, 36(2): 78-80. [20] GILLESPIE D T. The chemical Langevin equation[J]. Journal of Chemical Physics, 2000, 113(1): 297-306. [21] KERMACK W O, MCKENDRICK A G. A contribution to the mathematical theory of epidemics[J]. Bulletin of Mathematical Biology, 1991, 53(1/2): 57-87. [22] BECAR R, GONZALEZ P A, VASQUEZ Y. Fermionic greybody factors of two and five-dimensional dilatonic black holes[J]. European Physical Journal C, 2014, 74(8): 1-8. [23] WANG W D, ZHAO X Q. Threshold dynamics for compartmental epidemic models in periodic environments[J]. Journal of Dynamics and Differential Equations, 2008, 20(3): 699-717. [24] WANG X, XIAO Y N, WANG J R, et al. Stochastic disease dynamics of a hospital infection model[J]. Mathematical Biosciences, 2013, 241(1): 115-124. [25] KEELING M J, ROHANI P. Modeling Infectious Diseases in Humans and Animals[M]. Princeton: Princeton University Press, 2007. [26] CHAMPION V L, SKINNER C S. In Health Behaviour and Health Education: Theory, Research, and Practice [M]. 4th ed. San Francisco: John Wiley & Sons, 2008. [27] DURHAM D P, CASMAN E A. Incorporating individual health-protective decisions into disease transmission models: a mathematical framework[J]. Journal of Royal Society Interface, 2012, 9(2012): 562-570. [28] WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(1998): 440-442. [29] NEWMAN M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167-256. [30] HOLLAND M D, HASTINGS A. Strong effect of dispersal network structure on ecological dynamics[J]. Nature, 2012, 456(2012): 792-794. [31] NEWMAN M E J, WATTS D J. Renormalization group analysis of the small-world network model[J]. Physics Letters A, 1999, 263(1999): 341-346. -




 下载:
下载:









 渝公网安备50010802005915号
渝公网安备50010802005915号