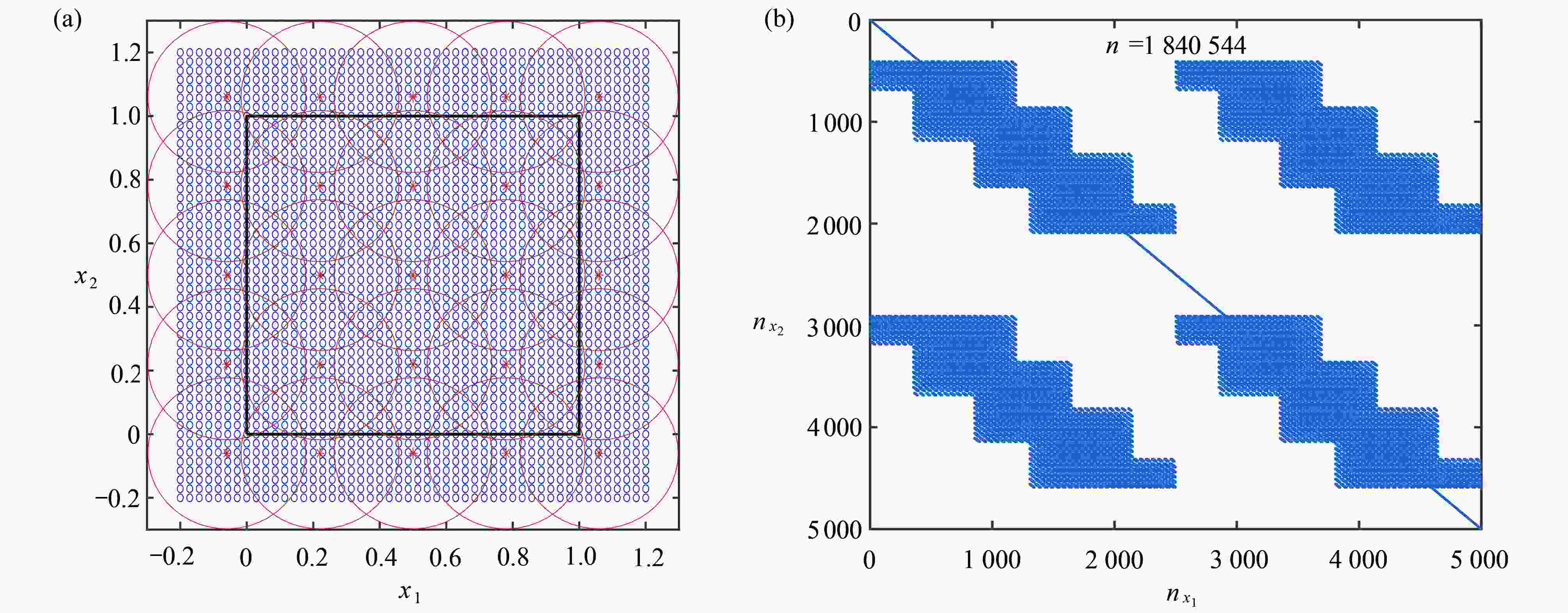
The RBF-PU Method for Solving 2D Nonlocal Diffusion and Peridynamic Equations
-
摘要:
采用单位分解径向基函数(radial basis function partition of unity,RBF-PU)方法,数值求解了二维非局部扩散问题和近场动力学问题。主要思想是对求解区域进行局部划分,在局部子区域上分别进行函数逼近,然后加权得到未知函数的全局逼近。这种基于方程强形式的径向基函数方法在求解非局部问题时,不需要处理网格与球形邻域求交的问题,避免了额外的一层积分计算,实施简便,计算量小。数值实验显示计算结果与解析解吻合较好,RBF-PU方法可以准确有效地求解非局部扩散方程和近场动力学方程。
Abstract:The radial basis function partition of unity (RBF-PU) method was applied to obtain the numerical solution of 2D nonlocal diffusion and peridynamic problems. The main idea is to partition the original domain into several patches, use the RBF approximation on each local domain, and then give weighting to obtain the global approximation of the unknown function. The radial basis function method based on the strong form of the equation has many advantages, such as avoiding an additional layer of integral calculation, no need to deal with intersections of neighborhoods with the mesh, and easiness of implementation. The numerical results show that, this method can solve nonlocal diffusion equations and peridynamic equations accurately and efficiently.
-
Key words:
- RBF interpolation /
- partition of unity /
- nonlocal diffusion /
- peridynamics
-
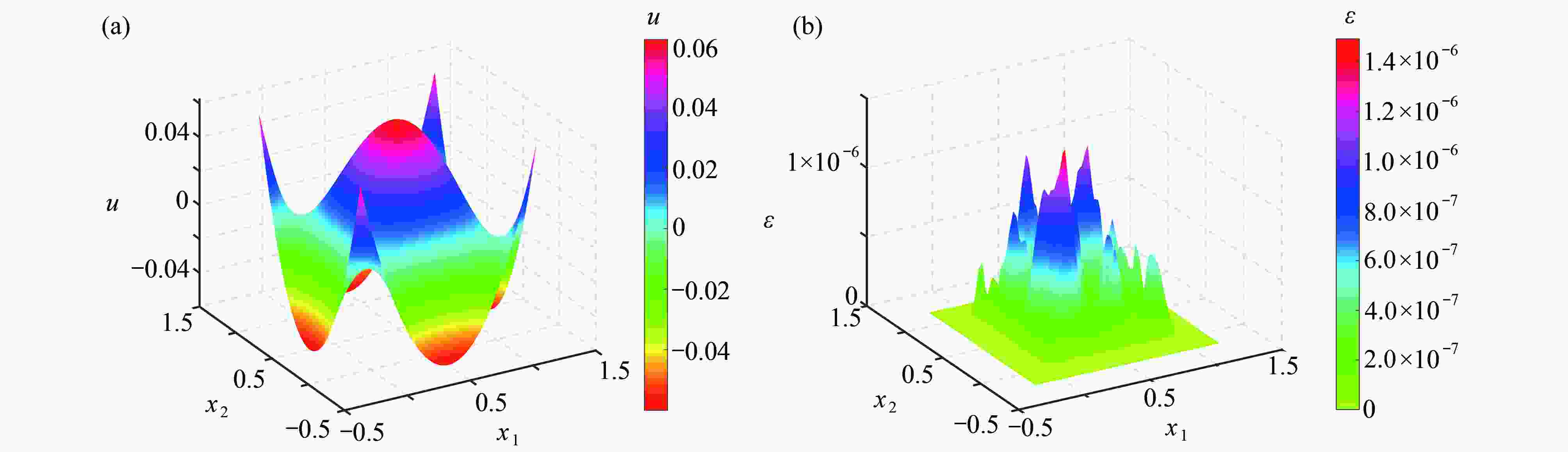
表 1 均匀离散非局部扩散方程数值结果(
$\delta = 0.2$ )Table 1. Numerical results of the nonlocal diffusion equation under uniform discretization (
$\delta = 0.2$ )h ${\varepsilon _{\max } }$ ${\varepsilon _{ {\rm{RMSE} } } }$ ${\varepsilon _{ {\rm{RE} } } }$ $N$ $t/{\rm{s}}$ $1/10$ $2.392\;362{\rm{E}}-2$ $5.340\;460{\rm{E}}-3$ $1.596\;423{\rm{E}}-1$ $5.103\;764{\rm{E}}+2$ $0.46$ $1/20$ $3.503\;622{\rm{E}}-4$ $1.012\;859{\rm{E}}-4$ $3.298\;962{\rm{E}}-3$ $2.028\;138{\rm{E}}+7$ $3.43$ $1/30$ $8.066\;769{\rm{E}}-6$ $2.375\;277{\rm{E}}-6$ $7.919\;804{\rm{E}}-5$ $8.778\;054{\rm{E}}+10$ $50.01$ $1/40$ $4.408\;203{\rm{E}}-6$ $9.530\;515{\rm{E}}-7$ $3.211\;906{\rm{E}}-5$ $5.302\;566{\rm{E}}+10$ $172.58$ $1/50$ $4.405\;356{\rm{E}}-6$ $1.227\;837{\rm{E}}-6$ $4.163\;255{\rm{E}}-5$ $2.130\;636{\rm{E}}+11$ $605.16$ $1/60$ $3.365\;385{\rm{E}}-5$ $6.696\;457{\rm{E}}-6$ $2.279\;511{\rm{E}}-4$ $4.492\;236{\rm{E}}+11$ $1\;481.48$ 表 2 离散非局部扩散方程的数值结果(
$\delta = 0.2$ )Table 2. Numerical results of the nonlocal diffusion equation under Halton discretization (
$\delta = 0.2$ )$h$ ${\varepsilon _{\max } }$ ${\varepsilon _{ {\rm{RMSE} } } }$ ${\varepsilon _{ {\rm{RE} } } }$ $N$ $t/{\rm{s}}$ $1/10$ $2.679\;438{\rm{E}}-2$ $6.772\;052{\rm{E}}-3$ $2.370\;566{\rm{E}}-1$ $3.206\;995{\rm{E}}+4$ $0.52$ $1/20$ $7.466\;535{\rm{E}}-4$ $1.795\;671{\rm{E}}-4$ $6.252\;326{\rm{E}}-3$ $1.842\;649{\rm{E}}+8$ $5.49$ $1/30$ $5.920\;469{\rm{E}}-6$ $1.175\;443{\rm{E}}-6$ $4.070\;005{\rm{E}}-5$ $1.805\;258{\rm{E}}+11$ $64.71$ $1/40$ $1.246\;481{\rm{E}}-5$ $2.040\;146{\rm{E}}-6$ $7.077\;887{\rm{E}}-5$ $8.713\;394{\rm{E}}+11$ $173.02$ $1/50$ $3.738\;273{\rm{E}}-6$ $1.029\;311{\rm{E}}-6$ $3.570\;744{\rm{E}}-5$ $2.862\;032{\rm{E}}+11$ $599.20$ $1/60$ $1.798\;596{\rm{E}}-6$ $4.251\;399{\rm{E}}-7$ $1.472\;884{\rm{E}}-5$ $7.453\;951{\rm{E}}+10$ $1\;511.76$ 表 3 模型的
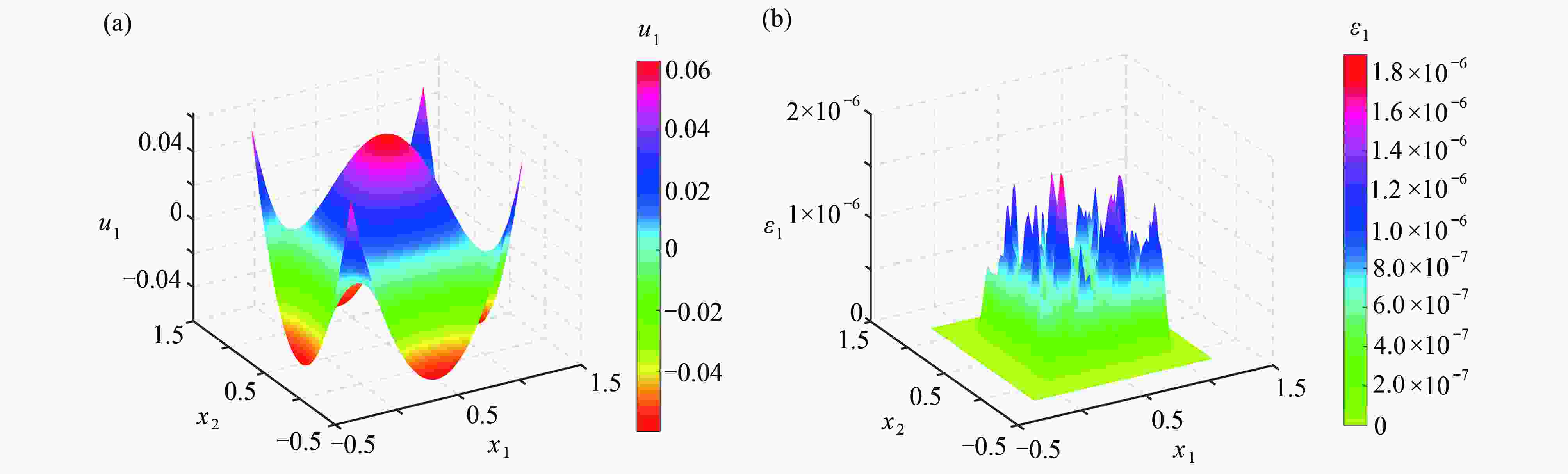
$x$ 方向位移的数值解$u_{1}$ ($\delta = 0.2$ )Table 3. Numerical results of displacement in the
$x$ direction for the peridynamic model$u_{1}$ ($\delta = 0.2$ )h ${\varepsilon _{\max } }$ ${\varepsilon _{ {\rm{RMSE} } } }$ ${\varepsilon _{ {\rm{RE} } } }$ $N$ $t/{\rm{s}}$ $1/10$ $9.242\;8{\rm{E}}-1$ $3.507\;7{\rm{E}}-1$ $1.048\;5{\rm{E}}+1$ $3.56{\rm{E}}+4$ $0.74$ $1/20$ $3.084\;2{\rm{E}}-2$ $6.767\;5{\rm{E}}-3$ $2.204\;2{\rm{E}}-1$ $1.00{\rm{E}}+6$ $3.79$ $1/30$ $4.183\;5{\rm{E}}-4$ $7.338\;0{\rm{E}}-5$ $2.446\;7{\rm{E}}-3$ $1.89{\rm{E}}+10$ $34.05$ $1/40$ $3.455\;7{\rm{E}}-4$ $5.556\;9{\rm{E}}-5$ $1.872\;7{\rm{E}}-3$ $5.38{\rm{E}}+11$ $75.71$ $1/50$ $3.072\;6{\rm{E}}-5$ $5.480\;6{\rm{E}}-6$ $1.858\;3{\rm{E}}-4$ $8.93{\rm{E}}+10$ $188.79$ 表 4 模型的
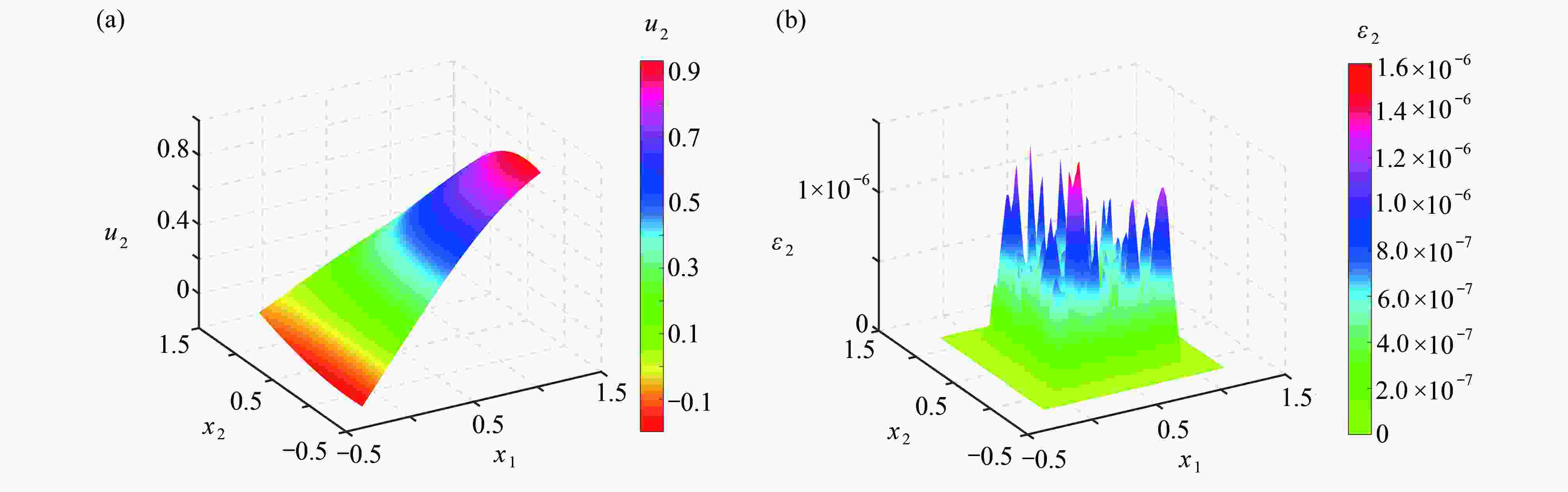
$y$ 方向位移数值解$u_{2}$ ($\delta = 0.2$ )Table 4. Numerical results of displacement in the
$y$ direction for the peridynamic model$u_{2}$ ($\delta = 0.2$ )h ${\xi _{\max } }$ ${\xi _{ {\rm{RMSE} } } }$ ${\xi _{ {\rm{RE} } } }$ $N$ $t/{\rm{s}}$ $1/10$ $2.674\;1{\rm{E}}-1$ $7.270\;6{\rm{E}}-2$ $1.551\;5{\rm{E}}-1$ $3.56{\rm{E}}+4$ $0.74$ $1/20$ $3.168\;0{\rm{E}}-2$ $7.372\;5{\rm{E}}-3$ $1.583\;9{\rm{E}}-2$ $1.00{\rm{E}}+6$ $3.79$ $1/30$ $3.069\;2{\rm{E}}-4$ $5.738\;3{\rm{E}}-5$ $1.235\;5{\rm{E}}-4$ $1.89{\rm{E}}+10$ $34.05$ $1/40$ $1.803\;9{\rm{E}}-4$ $3.851\;6{\rm{E}}-5$ $8.302\;3{\rm{E}}-5$ $5.38{\rm{E}}+11$ $75.71$ $1/50$ $3.037\;0{\rm{E}}-5$ $6.134\;8{\rm{E}}-6$ $1.323\;2{\rm{E}}-5$ $8.93{\rm{E}}+10$ $188.79$ -
[1] BOBARU F, MONCHAI D. The peridynamic formulation for transient heat conduction[J]. International Journal of Heat and Mass Transfer, 2010, 53(19/20): 4047-4059. [2] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. Analysis and approximation of nonlocal diffusion problems with volume constraints[J]. SIAM Review, 2012, 54(4): 667-696. doi: 10.1137/110833294 [3] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209. doi: 10.1016/S0022-5096(99)00029-0 [4] SILLING S A, EPTON M, WECKER O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2): 151-184. doi: 10.1007/s10659-007-9125-1 [5] 黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 61-70. (HUANG Dan, ZHANG Qin, QIAO Pizhong, et al. A review on peridynamics(PD) method and its application[J]. Advances in Mechanics, 2010, 40(4): 61-70.(in Chinese)HUANG Dan, ZHANG Qin, QIAO Pizhong, et al. A review on peridynamics(PD) method and its application[J]. Advances in Mechanics, 2010, 40(4): 61-70. (in Chinese)) [6] GU X, ZHANG Q, MADENCI E. Refined bond-based peridynamics for thermal diffusion[J]. Engineering Computations, 2019, 36(8): 2557-2587. doi: 10.1108/EC-09-2018-0433 [7] 李天一, 章青, 夏晓舟, 等. 考虑混凝土材料非均质特性的近场动力学模型[J]. 应用数学和力学, 2018, 39(8): 913-924. (LI Tianyi, ZHANG Qing, XIA Xiaozhou, et al. A peridynamic model for heterogeneous concrete materials[J]. Applied Mathematics and Mechanics, 2018, 39(8): 913-924.(in Chinese)LI Tianyi, ZHANG Qing, XIA Xiaozhou, et al. A peridynamic model for heterogeneous concrete materials[J]. Applied Mathematics and Mechanics, 2018, 39(8): 913-924. (in Chinese)) [8] SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers and Structures, 2005, 83(17/18): 1526-1535. [9] CHEN X, GUNZBURGER M. Continuous and discontinuous finite element methods for a peridynamics model of mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(9/12): 1237-1250. [10] WANG H, TIAN H. A fast Galerkin method with efficient matrix assembly and storage for a peridynamic model[J]. Journal of Computational Physics, 2012, 231(23): 7730-7738. doi: 10.1016/j.jcp.2012.06.009 [11] TIAN H, WANG H, WANG W. An efficient collocation method for a nonlocal diffusion model[J]. International Journal of Numerical Analysis and Modeling, 2013, 10(4): 815-825. [12] WANG C, WANG H. A fast collocation method for a variable-coefficient nonlocal diffusion model[J]. Journal of Computational Physics, 2017, 330: 114-126. doi: 10.1016/j.jcp.2016.11.003 [13] WANG H, TIAN H. A fast and faithful collocation method with efficient matrix assembly for a two-dimensional nonlocal diffusion model[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 273: 19-36. doi: 10.1016/j.cma.2014.01.026 [14] TIAN X C, DU Q. Analysis and comparison of different approximations to nonlocal diffusion and linear peridynamic equations[J]. SIAM Journal on Numerical Analysis, 2013, 51(6): 3458-3482. doi: 10.1137/13091631X [15] LEHOUCQ R B, ROWE S T. A radial basis function Galerkin method for inhomogeneous nonlocal diffusion[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 299: 366-380. doi: 10.1016/j.cma.2015.10.021 [16] ZHAO W, HON Y C, STOLL M. Localized radial basis functions-based pseudo-spectral method (LRBF-PSM) for nonlocal diffusion problems[J]. Computers and Mathematics With Applications, 2017, 75(5): 1685-1704. [17] ZHAO W, HON Y C. An accurate and efficient numerical method for solving linear peridynamic models[J]. Applied Mathematical Modelling, 2019, 74: 113-131. doi: 10.1016/j.apm.2019.04.039 [18] PASETTO M, LENG Y, CHEN J, et al. A reproducing kernel enhanced approach for peridynamic solutions[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 340: 1044-1078. doi: 10.1016/j.cma.2018.05.010 [19] DU Q, YIN X B. A conforming DG method for linear nonlocal models with integrable kernels[J]. Journal of Scientific Computing, 2019, 80(3): 1913-1935. doi: 10.1007/s10915-019-01006-0 [20] ZHANG S Y, NIE Y F. A POD-based fast algorithm for the nonlocal unsteady problems[J]. International Journal of Numerical Analysis and Modeling, 2020, 17(6): 858-871. [21] LIANG X, WANG L J, XU J F, et al. The boundary element method of peridynamics[R/OL]. 2021(2021-06-16) [2021-10-29].https://arxiv.org/abs/2009.08008. [22] LU J X, NIE Y F. A collocation method based on localized radial basis functions with reproducibility for nonlocal diffusion models[J]. Computational and Applied Mathematics, 2021, 40(8): 271-294. doi: 10.1007/s40314-021-01665-6 [23] 洪文强, 徐绩青, 许锡宾, 等. 求解Bratu型方程的径向基函数逼近法[J]. 应用数学和力学, 2016, 37(6): 617-625. (HONG Wenqiang, XU Jiqing, XU Xibin, et al. The radial basis function approximation method for solving Bratu-type equations[J]. Applied Mathematics and Mechanics, 2016, 37(6): 617-625.(in Chinese) doi: 10.3879/j.issn.1000-0887.2016.06.007HONG Wenqiang, XU Jiqing, XU Xibin, et al. The radial basis function approximation method for solving Bratu-type equations[J]. Applied Mathematics and Mechanics, 2016, 37(6): 617-625. (in Chinese)) doi: 10.3879/j.issn.1000-0887.2016.06.007 [24] 李怡, 吴林键, 舒丹, 等. 基于Gauss全局径向基函数的近岸浅水变形波高数值计算新方法[J]. 应用数学和力学, 2014, 35(8): 903-912. (LI Yi, WU Linjian, SHU Dan, et al. A new method to calculate the wave height of deformed shallow water based on the gauss global radial basis function[J]. Applied Mathematics and Mechanics, 2014, 35(8): 903-912.(in Chinese) doi: 10.3879/j.issn.1000-0887.2014.08.008LI Yi, WU Linjian, SHU Dan, et al. A new method to calculate the wave height of deformed shallow water based on the gauss global radial basis function[J]. Applied Mathematics and Mechanics, 2014, 35(8): 903-912. (in Chinese)) doi: 10.3879/j.issn.1000-0887.2014.08.008 [25] WENDLAND H. Scattered Data Approximation[M]. Cambridge: Cambridge University Press, 2005. [26] SHEPARD D. A two-dimensional interpolation function for irregularly-spaced data[C]//Proceedings of the 1968 23rd ACM National Conference (ACM 68). New York: Association for Computing Machinery, 1968: 517-524. -




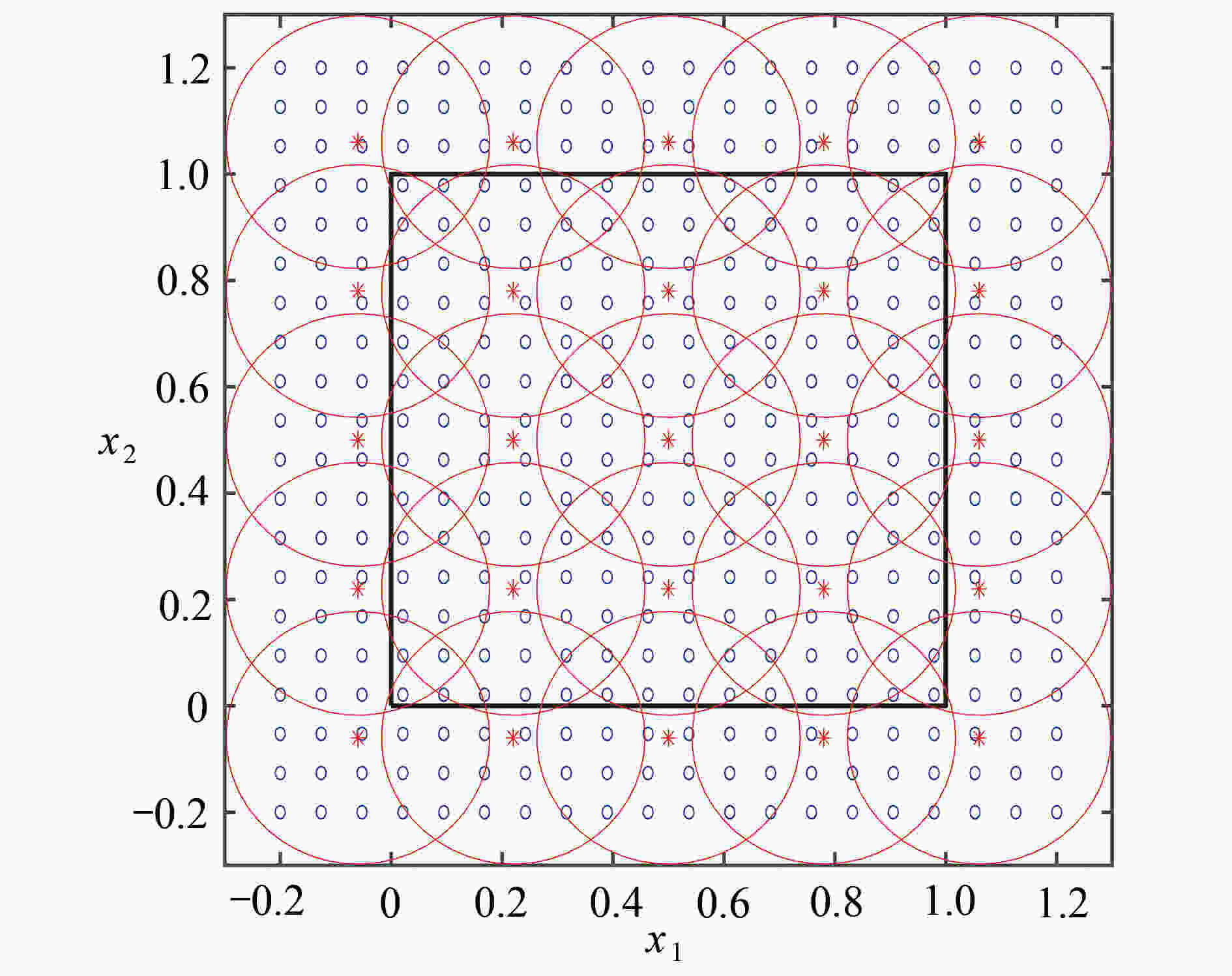
 下载:
下载:
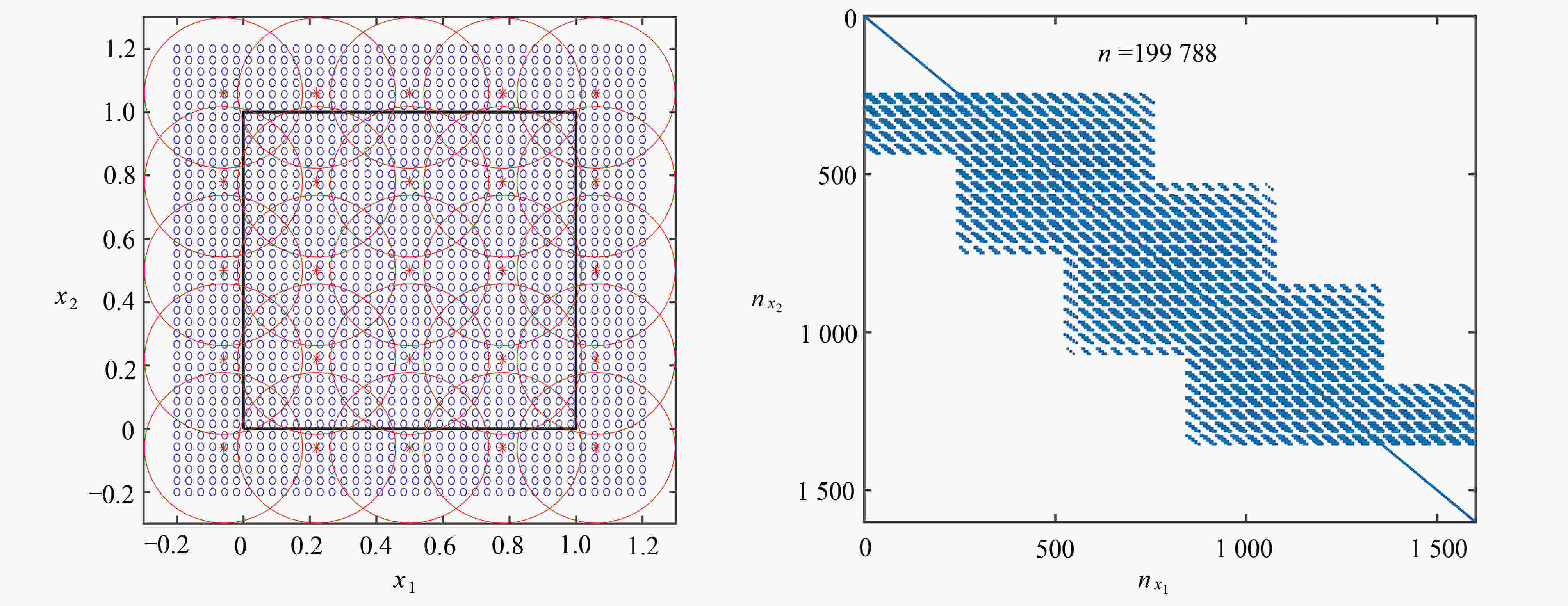
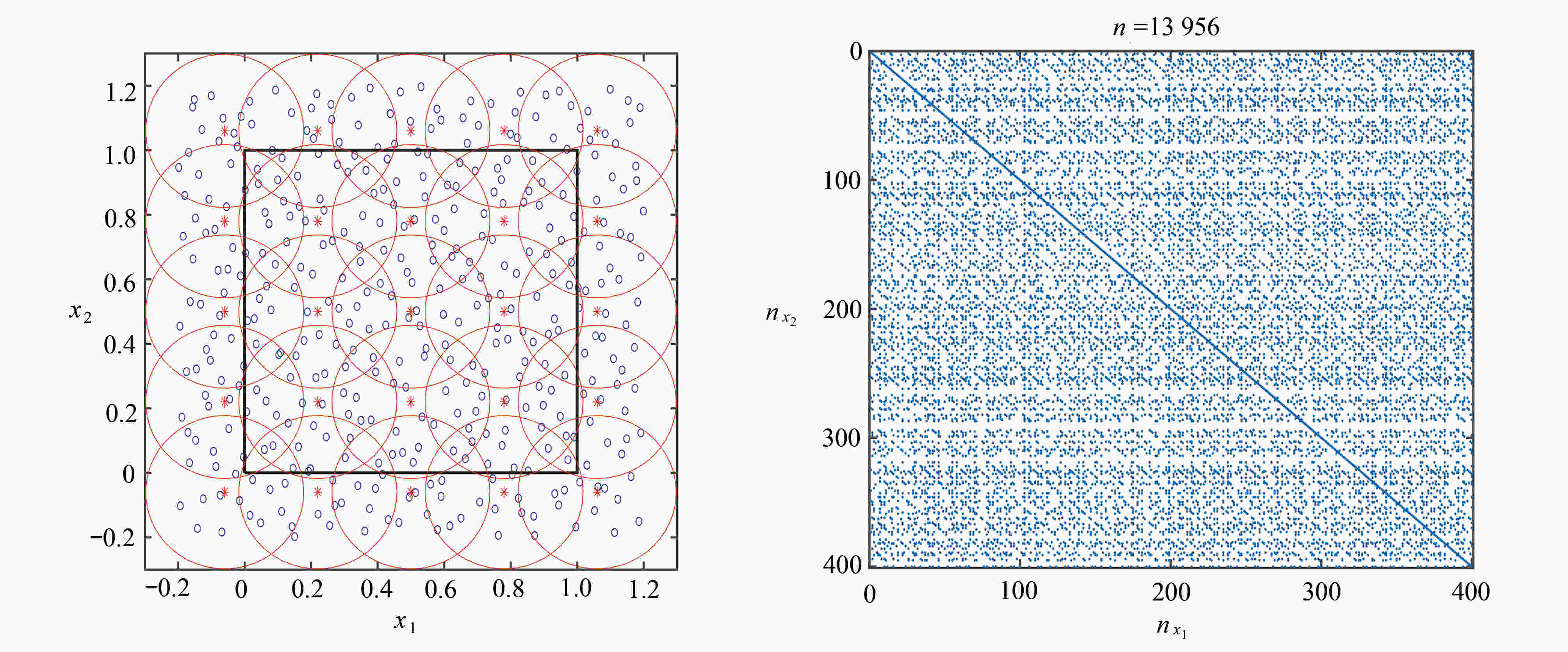






















 渝公网安备50010802005915号
渝公网安备50010802005915号