Research Progresses of Wavelet Methods and Their Applications in Mechanics
-
摘要:
小波理论在进行信号处理与函数逼近时体现出非常独特的时频局部性与多分辨分析能力,小波基函数则可兼具正交性、紧支性、低通滤波与插值性等优良的数学性质,这均使得小波分析理论在计算数学与计算力学领域具有很大的应用潜力,也进一步为这些领域的突破性发展带来了新的契机。自20世纪90年代以来,大量的研究已经证明,基于小波理论的数值方法在微分方程求解中具有非常明显的优势,但与此同时也暴露出了一些由小波基函数本身与其特有逼近方式所造成的数值计算应用局限。为了促进小波理论在计算数学与力学领域的创新性应用,给研究人员提供新的研究视角,该文简要梳理了小波分析的发展背景以及基于小波理论的数值方法的研究历史,并着重讨论分析了后者所面临的问题,以及近年来针对这些问题中的基础性难题所取得的研究进展。这些总结与评述有望为后续进一步发展并完善基于小波理论的定量数学求解方法,以及拓展其在力学乃至广泛工程问题求解中的应用提供有意义的参考。
Abstract:The wavelet theory shows very unique time-frequency localization and multi-resolution analysis ability in signal processing and function approximation. The wavelet basis function has excellent mathematical properties such as orthogonality, compactness, low-pass filtering and interpolation, which endows the wavelet analysis theory with great application potential in the fields of computational mathematics and computational mechanics, and creates new opportunities for breakthrough development in these fields. Since the 1990s, a large number of studies have proved that the numerical method based on the wavelet theory has very obvious advantages in solving differential equations, but at the same time, have exposed some limitations of numerical calculation application caused by the wavelet basis function itself and its unique approximation method. In order to promote the innovative application of the wavelet theory in the fields of computational mathematics and mechanics and provide researchers with a new research perspective, the development background of the wavelet analysis and the research history of methods based on the wavelet theory were reviewed, and the numerical method problems were emphasized and the research progresses made in recent years discussed. The conclusions and comments may provide a meaningful reference for the further development and improvement of quantitative mathematical solution methods based on the wavelet theory and applications in mechanics as well as solutions of a wide range of engineering problems.
-
-
[1] CHAMPENEY D C. A handbook of Fourier Theorems[M]. Cambridge: Cambridge University Press, 1987. [2] GABOR D. Theory of communication, part 1: the analysis of information[J]. Journal of the Institution of Electrical Engineers, Part Ⅲ: Radio and Communication Engineering, 1946, 93(26): 429-441. doi: 10.1049/ji-3-2.1946.0074 [3] CRANDALL R E. Projects in Scientific Computation[M]. Springer, 1995. [4] 刘小靖, 王加群, 周又和, 等. 小波方法及其非线性力学问题应用分析[J]. 固体力学学报, 2017, 38(4): 287-311. (LIU Xiaojing, WANG Jiaqun, ZHOU Youhe, et al. Wavelet methods and applications in nonlinear mechanics problems[J]. Acta Mechanica Solida Sinica, 2017, 38(4): 287-311.(in Chinese) [5] JAMESON L, ADACHI T, UKAI O, et al. Wavelet-based numerical methods[J]. International Journal of Computational Fluid Dynamics, 1998, 10(4): 267-280. doi: 10.1080/10618569808961690 [6] LATTO A, RESNIKOFF H, TENENBAUM E. The evaluation of connection coefficients of compactly supported wavelets[C]//French-USA Workshop on Wavelets and Turbulence. Springer, 1991. [7] XU J C, SHANN W C. Galerkin-wavelet methods for two-point boundary value problem[J]. Numerische Mathematik, 1992, 63(1): 123-142. doi: 10.1007/BF01385851 [8] TANAKA S, OKADAD H, OKAZAWA S. A wavelet Galerkin method employing B-spline bases for solid mechanics problems without the use of a fictitious domain[J]. Computational Mechanics, 2012, 50(1): 35-48. doi: 10.1007/s00466-011-0671-9 [9] 王记增. 正交小波统一理论与方法及其在压电智能结构等力学研究中的应用[D]. 博士学位论文. 兰州: 兰州大学, 2001.WANG Jizeng. Generalized theory and arithmetic of orthogonal wavelets and applications to researches of mechanics including piezoelectric smart structures[D]. PhD Thesis. Lanzhou: Lanzhou University, 2001. (in Chinese) [10] ZHANG L, WANG J Z, ZHOU Y H. Wavelet solution for large deflection bending problems of thin rectangular plates[J]. Archive of Applied Mechanics, 2015, 85(3): 355-365. doi: 10.1007/s00419-014-0960-9 [11] ZHANG L, WANG J Z, ZHOU Y H. Large deflection and post-buckling analysis of non-linearly elastic rods by wavelet method[J]. International Journal of Non-Linear Mechanics, 2016, 78: 45-52. doi: 10.1016/j.ijnonlinmec.2015.10.002 [12] NAKAGOSHI S, NOGUCHI H. A modified wavelet Galerkin method for analysis of Mindlin plates[J]. JSME International Journal Series A: Solid Mechanics and Material Engineering, 2001, 44(4): 610-615. doi: 10.1299/jsmea.44.610 [13] ALQASSAB M, NAIR S. Wavelet-Galerkin method for free vibrations of elastic cable[J]. Journal of Engineering Mechanics, 2003, 129(3): 350-357. doi: 10.1061/(ASCE)0733-9399(2003)129:3(350) [14] LI B, CHEN X F, MA J X. Detection of crack location and size in structures using wavelet finite element methods[J]. Journal of Sound and Vibration, 2005, 285(4/5): 767-782. [15] LI B, CHEN X F, HE Z. A wavelet-based error estimator and adaptive scheme for plate bending problems[J]. International Journal of Computational Methods, 2010, 7(2): 241-259. doi: 10.1142/S0219876210002155 [16] LI B, CHEN X F. Wavelet-based numerical analysis: a review and classification[J]. Finite Elements in Analysis and Design, 2014, 81: 14-31. doi: 10.1016/j.finel.2013.11.001 [17] 王记增, 周又和. 广义小波高斯积分法的误差估计[J]. 兰州大学学报(自然科学版), 1998, 34(2): 26-30. (WANG Jizeng, ZHOU Youhe. An error estimation of generalized Gaussian integral method in wavelet theory[J]. Journal of Lanzhou University(Natural Sciences) , 1998, 34(2): 26-30.(in Chinese) [18] 周又和, 王记增. 小波尺度函数计算的广义高斯积分法及其应用[J]. 数学物理学报, 1999, 19(3): 293-300. (ZHOU Youhe, WANG Jizeng. Generalized Gaussian integral method for calculations of scaling function transform of wavelets and its applications[J]. Acta Mathematica Scientia, 1999, 19(3): 293-300.(in Chinese) doi: 10.3321/j.issn:1003-3998.1999.03.008 [19] BERTOLUZZA S, NALDI G, RAVEL J C. Wavelet methods for the numerical solution of boundary value problems on the interval[J]. Wavelet Analysis and Its Applications, 1994, 5: 425-448. [20] BELYTSCHKO T, LU Y Y, GU L. Element−free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994, 37(2): 229-256. doi: 10.1002/nme.1620370205 [21] LIU G R. Meshfree Methods: Moving Beyond the Finite Element Method[M]. CRC Press, 2009. [22] MOUKALLED F, MANGANI L, DARWISH M. The Finite Volume Method in Computational Fluid Dynamics[M]. Springer, 2016. [23] DAUBECHIES I. Ten Lectures on Wavelets[M]. Society for Industrial and Applied Mathematics, 1992. [24] BROWN I J. A wavelet tour of signal processing: the sparse way[J]. Investigation Operacional, 2008, 29(3): 277-278. [25] DONOHO D L. Interpolating wavelet transforms[R]. Technical Report. Department of Statistics, Stanford University, 1992. [26] AMARATUNGA K, WILLIAMS J R. Wavelet based Green’s function approach to 2D PDEs[J]. Engineering Computations, 1993, 10(4): 349-367. doi: 10.1108/eb023913 [27] COHEN A, DAUBECHIES I, VIAL P. Wavelets on the interval and fast wavelet transforms[J]. Applied and Computational Harmonic Analysis, 1993, 1(1): 54-81. doi: 10.1006/acha.1993.1005 [28] XU C, WANG J Z, LIU X J, et al. Coiflet solution of strongly nonlinear p-Laplacian equations[J]. Applied Mathematics and Mechanics, 2017, 38(7): 1031-1042. doi: 10.1007/s10483-017-2212-6 [29] LIU X J, LIU G R, WANG J Z, et al. A wavelet multiresolution interpolation Galerkin method for targeted local solution enrichment[J]. Computational Mechanics, 2019, 64(4): 989-1016. doi: 10.1007/s00466-019-01691-6 [30] LIU X J, LIU G R, WANG J Z, et al. A wavelet multiresolution interpolation Galerkin method with effective treatments for discontinuity for crack growth analyses[J]. Engineering Fracture Mechanics, 2020, 225: 106836. doi: 10.1016/j.engfracmech.2019.106836 [31] LIU X J, LIU G R, WANG J Z, et al. A wavelet multi-resolution enabled interpolation Galerkin method for two-dimensional solids[J]. Engineering Analysis With Boundary Elements, 2020, 117: 251-268. doi: 10.1016/j.enganabound.2020.04.007 [32] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.WANG Xucheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003. (in Chinese) [33] TORO E F. Riemann Solvers and Numerical Methods for Fluid Dynamics: a Practical Introduction[M]. Springer, 2013. [34] ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1997, 43(2): 357-372. [35] ARORA S, JAIN R, KUKREJA V K. Solution of Benjamin-Bona-Mahony-Burgers equation using collocation method with quintic Hermite splines[J]. Applied Numerical Mathematics, 2020, 154: 1-16. doi: 10.1016/j.apnum.2020.03.015 [36] KARAKOÇ S B G, ZEYBEK H. Solitary-wave solutions of the GRLW equation using septic B-spline collocation method[J]. Applied Mathematics and Computation, 2016, 289: 159-171. doi: 10.1016/j.amc.2016.05.021 [37] PERIC D, OWEN D R J. Finite-element applications to the nonlinear mechanics of solids[J]. Reports on Progress in Physics, 1998, 61(11): 1495-1574. doi: 10.1088/0034-4885/61/11/002 [38] BLAISDELL G A, SPYROPOULOS E T, QIN J H. The effect of the formulation of nonlinear terms on aliasing errors in spectral methods[J]. Applied Numerical Mathematics, 1996, 21(3): 207-219. doi: 10.1016/0168-9274(96)00005-0 [39] 张德良. 计算流体力学教程[M]. 北京: 高等教育出版社, 2010.ZHANG Deliang. A Course in Computational Fluid Dynamics[M]. Beijing: Higher Education Press, 2010. (in Chinese) [40] ZHOU Y H. Wavelet Numerical Method and Its Applications in Nonlinear Problems[M]. Singapore: Springer, 2021. [41] 张磊. 高精度小波数值方法及其在结构非线性分析中的应用[D]. 博士学位论文. 兰州: 兰州大学, 2016.ZHANG Lei. High-precision wavelet numerical methods and applications to nonlinear structure analysis[D]. PhD Thesis. Lanzhou: Lanzhou University, 2016. (in Chinese) [42] 王记增, 王晓敏, 周又和. 基于正交小波尺度函数展开的强非线性微分方程求解[J]. 兰州大学学报(自然科学版), 2010, 46(5): 96-101. (WANG Jizeng, WANG Xiaoming, ZHOU Youhe. Numerical solutions to differential equations with strong nonlinearities based on series expansion of orthogonal scaling functions[J]. Journal of Lanzhou University (Natural Sciences) , 2010, 46(5): 96-101.(in Chinese) [43] 刘小靖, 王记增, 周又和. 一种适用于强非线性结构力学问题数值求解的修正小波伽辽金方法[J]. 固体力学学报, 2011, 32(3): 249-257. (LIU Xiaojing, WANG Jizeng, ZHOU Youhe. A modified wavelet-Galerkin method for computations in structural mechanics with strong nonlinearity[J]. Chinese Journal of Solid Mechanics, 2011, 32(3): 249-257.(in Chinese) [44] 刘小靖, 王记增, 周又和. 一种分析柔性梁超大挠度问题的小波算法[J]. 固体力学学报, 2013, 33(S1): 159-165. (LIU Xiaojing, WANG Jizeng, ZHOU Youhe. ZHOU Youhe. A wavelet method for studying large deflection bending problems of flexible beams[J]. Chinese Journal of Solid Mechanics, 2013, 33(S1): 159-165.(in Chinese) [45] WANG J Z, WANG X M, ZHOU Y H. A wavelet approach for active-passive vibration control of laminated plates[J]. Acta Mechanica Sinica, 2012, 28(2): 520-531. doi: 10.1007/s10409-012-0045-3 [46] LIU X J, ZHOU Y H, WANG X M, et al. A wavelet method for solving a class of nonlinear boundary value problems[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(8): 1939-1948. doi: 10.1016/j.cnsns.2012.12.010 [47] LIU X J, ZHOU Y H, ZHANG L, et al. Wavelet solutions of Burgers’ equation with high Reynolds numbers[J]. Science China Technological Sciences, 2014, 57(7): 1285-1292. doi: 10.1007/s11431-014-5588-z [48] WANG X M, LIU X J, WANG J Z, et al. A wavelet method for bending of circular plate with large deflection[J]. Acta Mechanica Solida Sinica, 2015, 28(1): 83-90. doi: 10.1016/S0894-9166(15)60018-0 [49] LIU X J, WANG J Z, ZHOU Y H. A space-time fully decoupled wavelet Galerkin method for solving two-dimensional Burgers’ equations[J]. Computers and Mathematics With Applications, 2016, 72(12): 2908-2919. doi: 10.1016/j.camwa.2016.10.016 [50] LIU X J, WANG J Z, ZHOU Y H. A space-time fully decoupled wavelet Galerkin method for solving a class of nonlinear wave problems[J]. Nonlinear Dynamics, 2017, 90(1): 599-616. doi: 10.1007/s11071-017-3684-x [51] WANG J Q, ZHOU Y H, LIU X J. A space-time fully decoupled wavelet Galerkin method for solving multidimensional nonlinear Schrödinger equations with damping[J]. Mathematical Problems in Engineering, 2017, 2017: 1-10. [52] WANG J Q, LIU X J, ZHOU Y H. A high-order accurate wavelet method for solving Schrödinger equations with general nonlinearity[J]. Applied Mathematics and Mechanics (English Edition) , 2018, 39(2): 275-290. doi: 10.1007/s10483-018-2299-6 [53] MA X, WU B, ZHANG J, et al. A new numerical scheme with wavelet-Galerkin followed by spectral deferred correction for solving string vibration problems[J]. Mechanism and Machine Theory, 2019, 142: 103623. doi: 10.1016/j.mechmachtheory.2019.103623 [54] TEMIMI H, BEN-ROMDHANE M, BACCOUCH M, et al. A two-branched numerical solution of the two-dimensional Bratu’s problem[J]. Applied Numerical Mathematics, 2020, 153: 202-216. doi: 10.1016/j.apnum.2020.02.010 [55] YU Q, XU H, LIAO S J. Coiflets solutions for Föppl-von Kármán equations governing large deflection of a thin flat plate by a novel wavelet-homotopy approach[J]. Numerical Algorithms, 2018, 79(4): 993-1020. doi: 10.1007/s11075-018-0470-x [56] YU Q, XU H, LIAO S J, et al. A novel homotopy-wavelet approach for solving stream function-vorticity formulation of Navier-Stokes equations[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 67: 124-151. doi: 10.1016/j.cnsns.2018.07.001 [57] WANG A, XU H, YU Q. Homotopy Coiflets wavelet solution of electrohydrodynamic flows in a circular cylindrical conduit[J]. Applied Mathematics and Mechanics (English Edition) , 2020, 41(5): 681-698. doi: 10.1007/s10483-020-2607-8 [58] CHEN Q B, XU H. Coiflet wavelet-homotopy solution of channel flow due to orthogonally moving porous walls governed by the Navier-Stokes equations[J]. Journal of Mathematics, 2020, 2020: 5739648. [59] YU Q. A hierarchical wavelet method for nonlinear bending of materially and geometrically anisotropic thin plate[J]. Communications in Nonlinear Science and Numerical Simulation, 2021, 92: 105498. doi: 10.1016/j.cnsns.2020.105498 [60] YU Q. Wavelet-based homotopy method for analysis of nonlinear bending of variable-thickness plate on elastic foundations[J]. Thin-Walled Structures, 2020, 157: 107105. doi: 10.1016/j.tws.2020.107105 [61] PALIWAL D N, PANDE A. Orthotropic cylindrical pressure vessels under line load[J]. International Journal of Pressure Vessels and Piping, 1999, 76: 455-459. doi: 10.1016/S0308-0161(99)00010-1 [62] BISHOP R E D, CANNON S M, MIAO S. On coupled bending and torsional vibration of uniform beams[J]. Journal of Sound and Vibration, 1989, 131: 457-464. doi: 10.1016/0022-460X(89)91005-5 [63] CHANDRASEKHAR S. Hydrodynamic and Hydromagnetic Stability[M]. Oxford: Oxford University Press, 1961. [64] NOOR M A, MOHYUD-DIN S T. Homotopy perturbation method for solving sixth-order boundary value problems[J]. Computers and Mathematics With Applications, 2008, 55(12): 2953-2972. doi: 10.1016/j.camwa.2007.11.026 [65] GOLBABAI A, JAVIDI M. Application of homotopy perturbation method for solving eighth-order boundary value problems[J]. Applied Mathematics and Computation, 2007, 191(2): 334-346. doi: 10.1016/j.amc.2007.02.091 [66] NOOR M A, MOHYUD-DIN S T. Variational iteration method for solving higher-order nonlinear boundary value problems using He’s polynomials[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2008, 9(2): 141-156. [67] LIU G R, WU T Y. Differential quadrature solutions of eighth-order boundary-value differential equations[J]. Journal of Computational and Applied Mathematics, 2002, 145(1): 223-235. doi: 10.1016/S0377-0427(01)00577-5 [68] WU T Y, LIU G R. The generalized differential quadrature rule for fourth-order differential equations[J]. International Journal for Numerical Methods in Engineering, 2001, 50(8): 1907-1929. doi: 10.1002/nme.102 [69] WU T Y, LIU G R. Application of generalized differential quadrature rule to sixth-order differential equations[J]. Communications in Numerical Methods in Engineering, 2000, 16(11): 777-784. doi: 10.1002/1099-0887(200011)16:11<777::AID-CNM375>3.0.CO;2-6 [70] BOUTAYEB A, TWIZELL E H. Finite-difference methods for the solution of special eighth-order boundary-value problems[J]. International Journal of Computer Mathematics, 1993, 48(1/2): 63-75. [71] BALLEM S, VISWANADHAM K N S K. Numerical solution of eighth order boundary value problems by Galerkin method with septic B-splines[J]. Procedia Engineering, 2015, 127: 1370-1377. doi: 10.1016/j.proeng.2015.11.496 [72] LANG F G, XU X P. Quartic B-spline collocation method for fifth order boundary value problems[J]. Computing, 2011, 92(4): 365. doi: 10.1007/s00607-011-0149-9 [73] SIDDIQI S S, TWIZELL E H. Spline solutions of linear eighth-order boundary-value problems[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 131: 309-325. doi: 10.1016/0045-7825(96)88162-X [74] SIDDIQI S S, TWIZELL E H. Spline solutions of linear twelfth-order boundary-value problems[J]. Journal of Computational and Applied Mathematics, 1997, 78(2): 371-390. doi: 10.1016/S0377-0427(96)00164-1 [75] JOHNSTON H, LEAKE C, MORTARI D. Least-squares solutions of eighth-order boundary value problems using the theory of functional connections[J]. Mathematics, 2020, 8(3): 397. doi: 10.3390/math8030397 [76] ZHANG L, WANG J Z, LIU X J, et al. A wavelet integral collocation method for nonlinear boundary value problems in physics[J]. Computer Physics Communications, 2017, 215: 91-102. doi: 10.1016/j.cpc.2017.02.017 [77] WENG J, LIU X J, ZHOU Y H, et al. A space-time fully decoupled wavelet integral collocation method with high-order accuracy for a class of nonlinear wave equations[J]. Mathematics, 2021, 9(22): 2957. doi: 10.3390/math9222957 [78] AMIN R, SHAH K, AL-MDALLAL Q M, et al. Efficient numerical algorithm for the solution of eight order boundary value problems by Haar wavelet method[J]. International Journal of Applied and Computational Mathematics, 2021, 7(2): 1-18. [79] AMIN R, SHAH K, KHAN I, et al. Efficient numerical scheme for the solution of tenth order boundary value problems by the Haar wavelet method[J]. Mathematics, 2020, 8(11): 1874. doi: 10.3390/math8111874 -




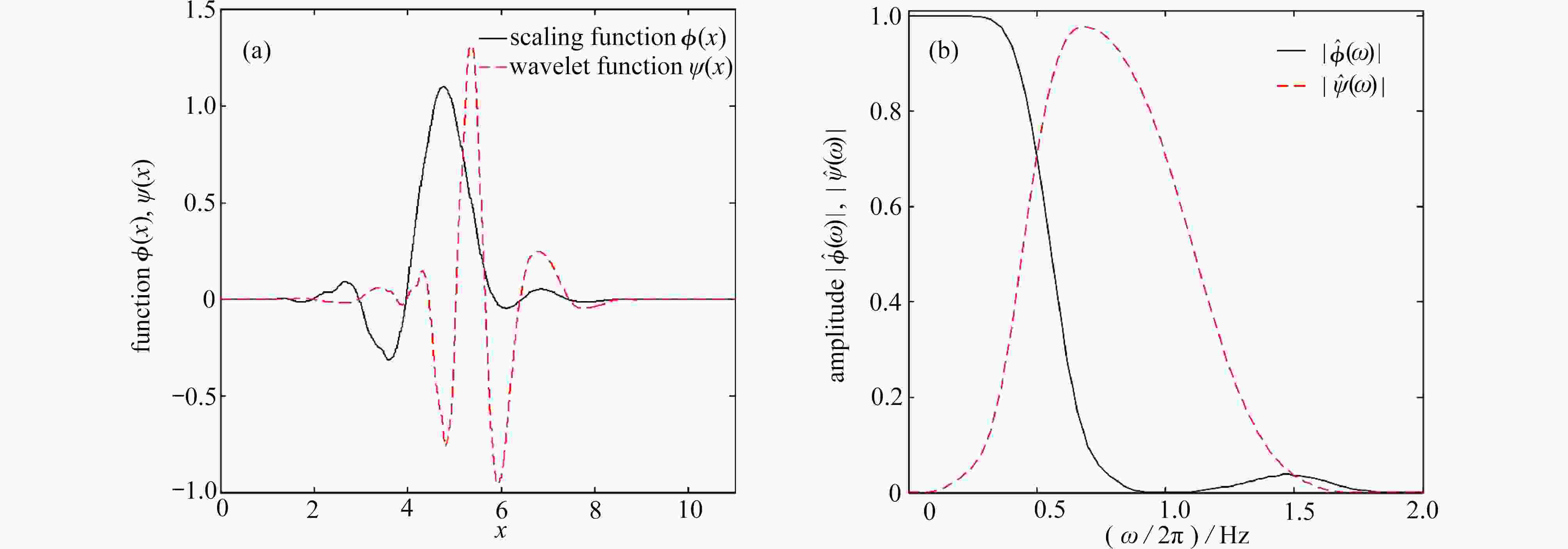




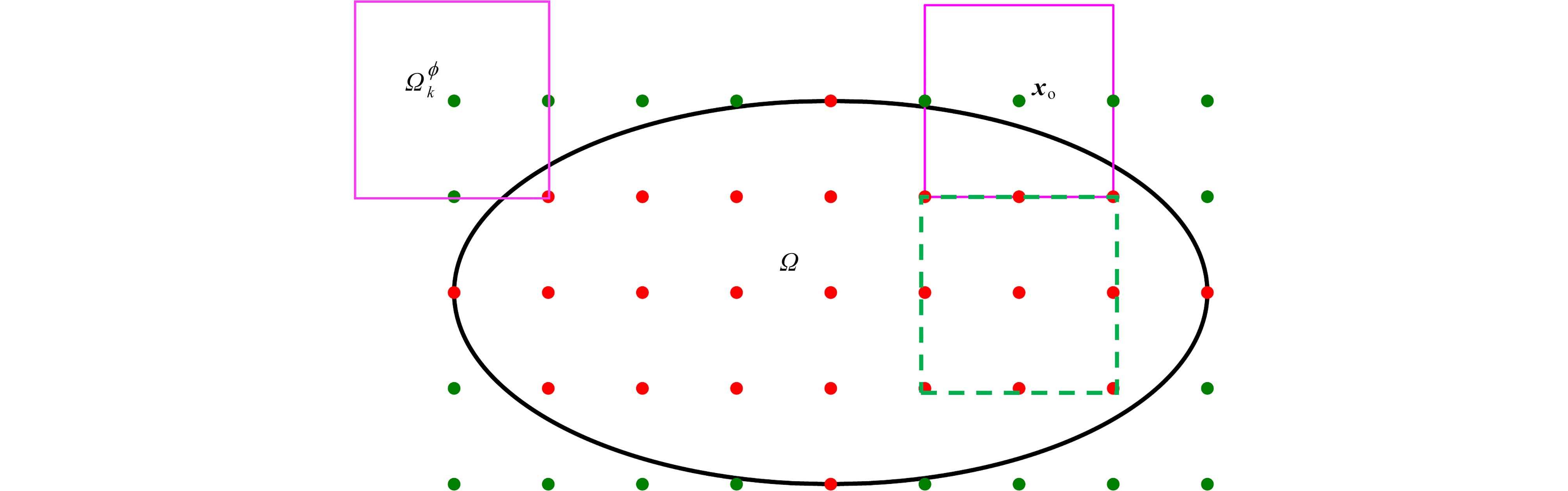
 下载:
下载:
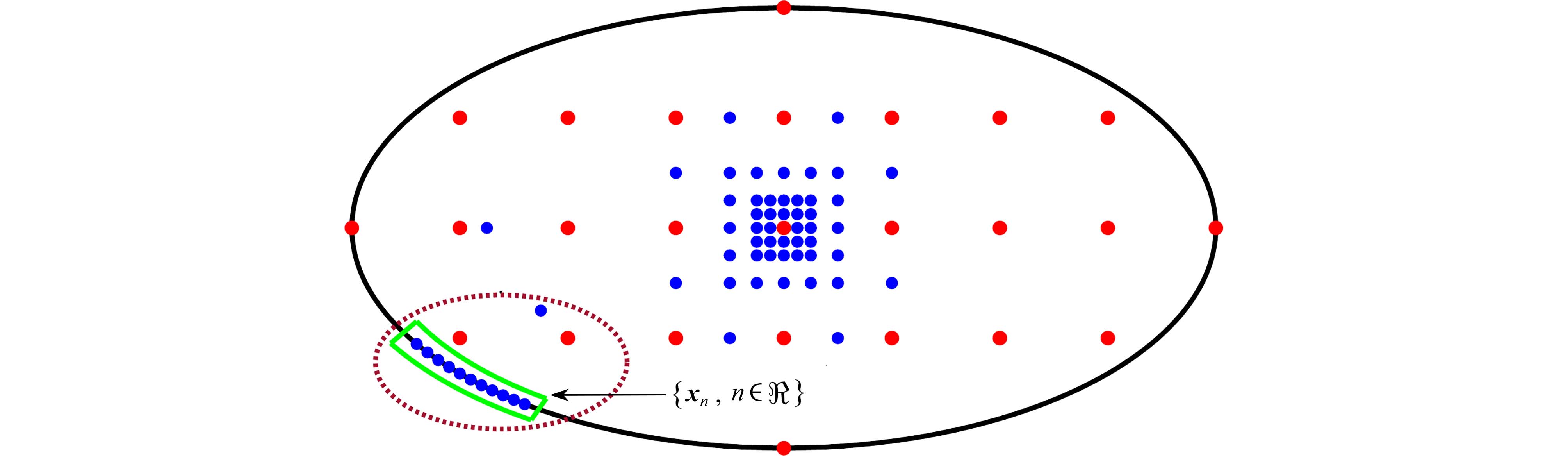


 渝公网安备50010802005915号
渝公网安备50010802005915号