A Calculation Model for Temperature Responses of Active Cooling Lattice Sandwich Structures for Thermal Protection
-
摘要:
针对点阵夹层结构主动热防护问题，建立了夹层结构面板和芯体导热与冷却剂对流耦合的非稳态传热理论模型，利用有限体积法离散控制方程并在MATLAB中进行了迭代求解。模型首次考虑了面板与夹芯杆之间的收缩热阻，并利用分离变量法得到了收缩热阻的近似解析解。基于单胞模型和周期性边界条件，模拟得到了模型所需的表面对流传热系数hb和hfin。最后，选取多单胞计算工况进行数值模拟和理论模型对比，并讨论了收缩热阻对模型预测精度的影响。结果表明：理论模型能够准确预测夹层结构及内部流体的温度变化，理论与仿真之间的最大误差不超过1%；随着外加热流密度不断增大，忽略收缩热阻使得计算结果造成的误差不断增大；与数值模拟相比，理论模型可显著地减少计算时间并节省计算资源，尤其适用于非均匀、非稳态复杂热载荷下点阵夹层结构的温度响应计算。
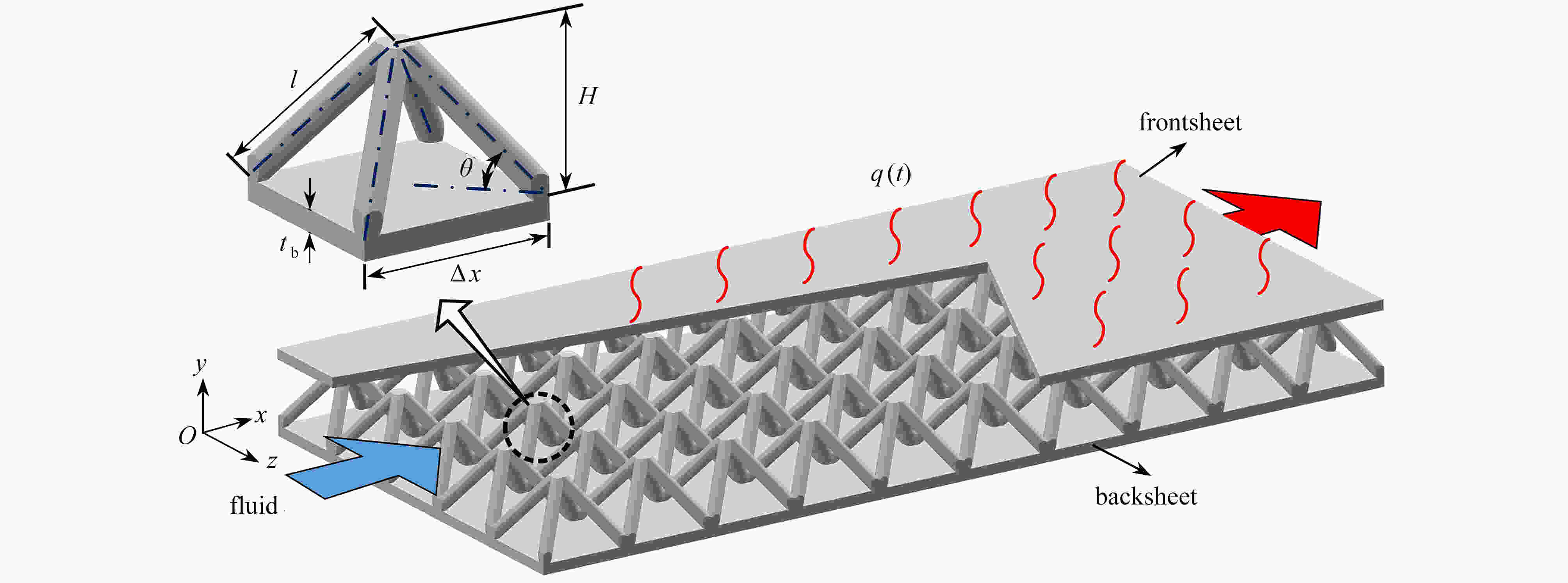
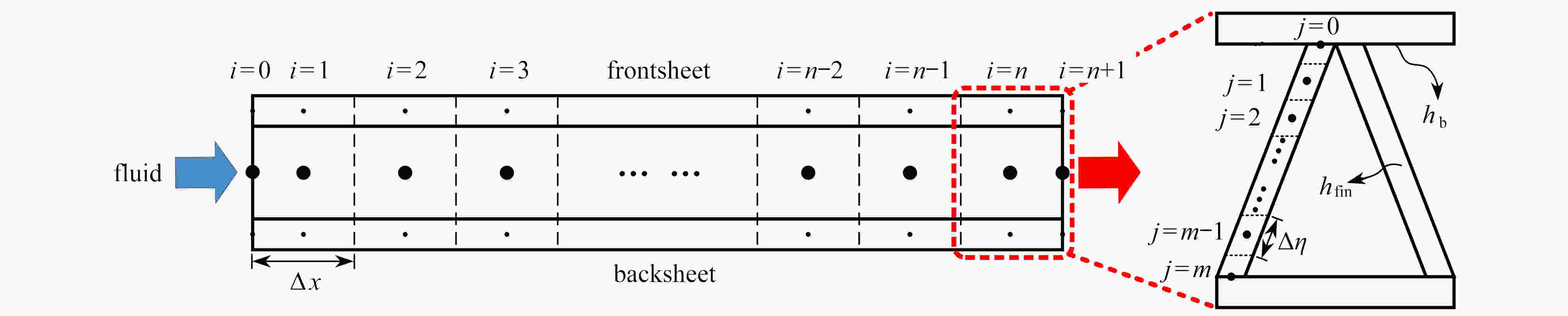
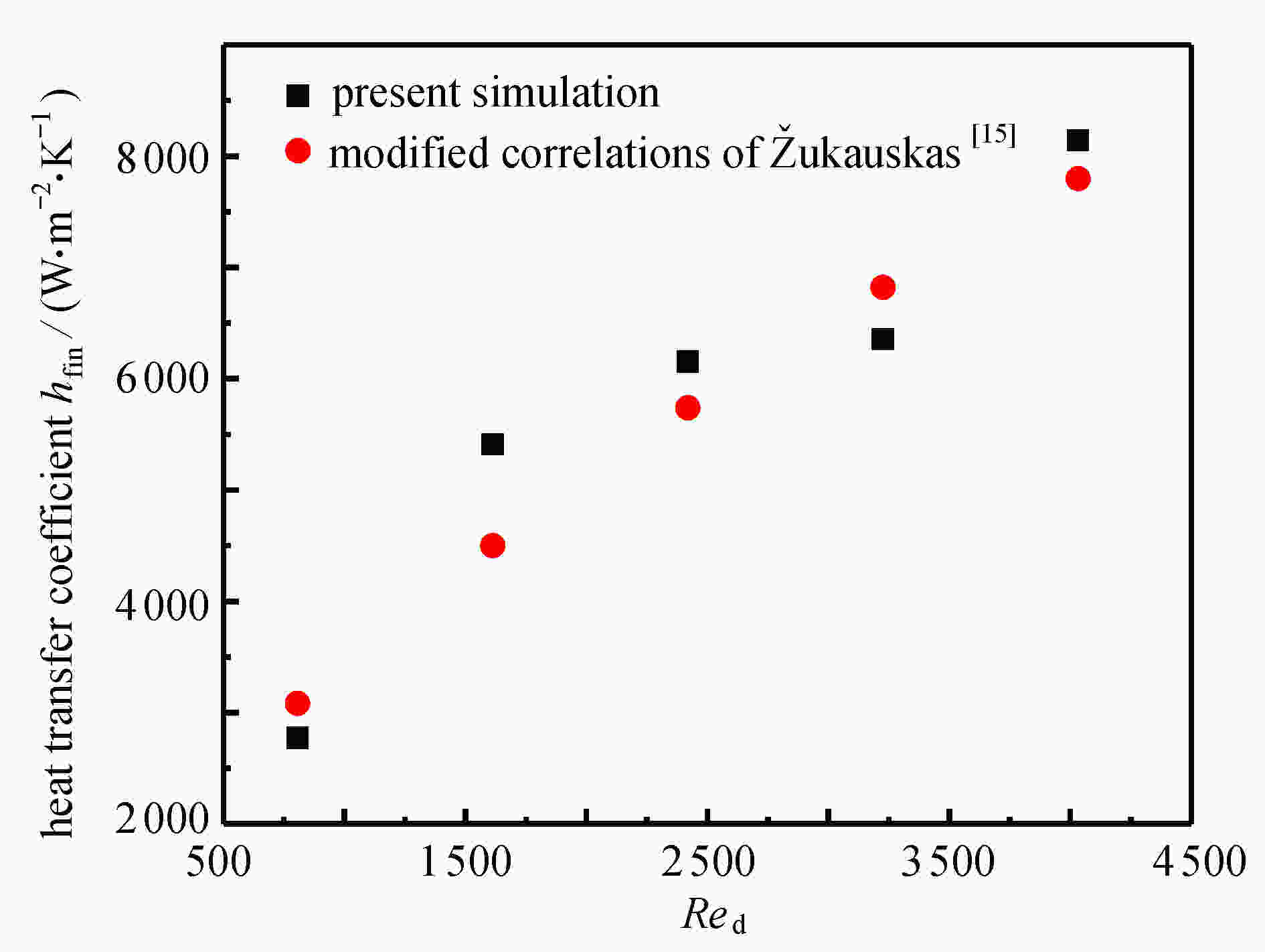
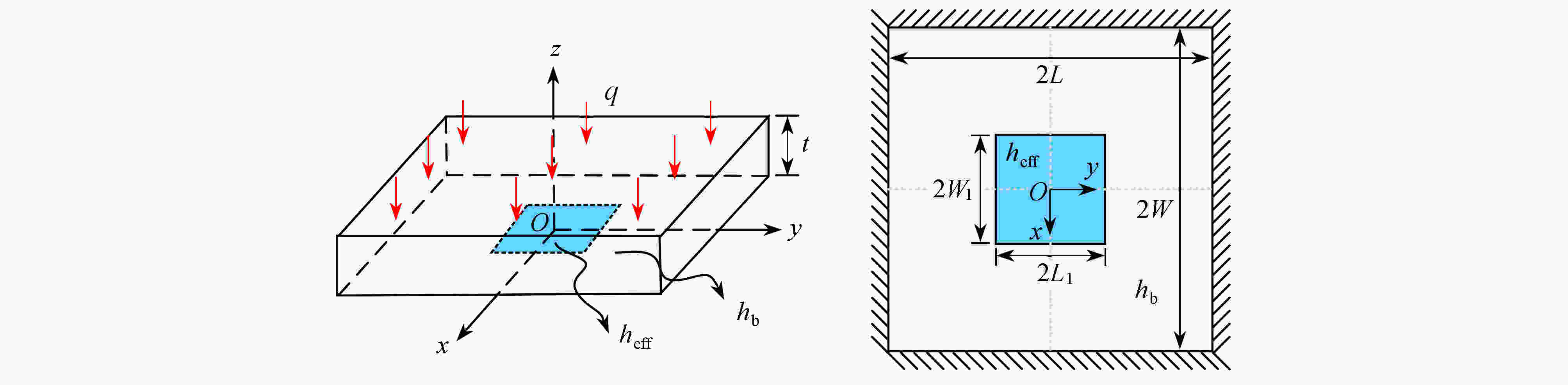
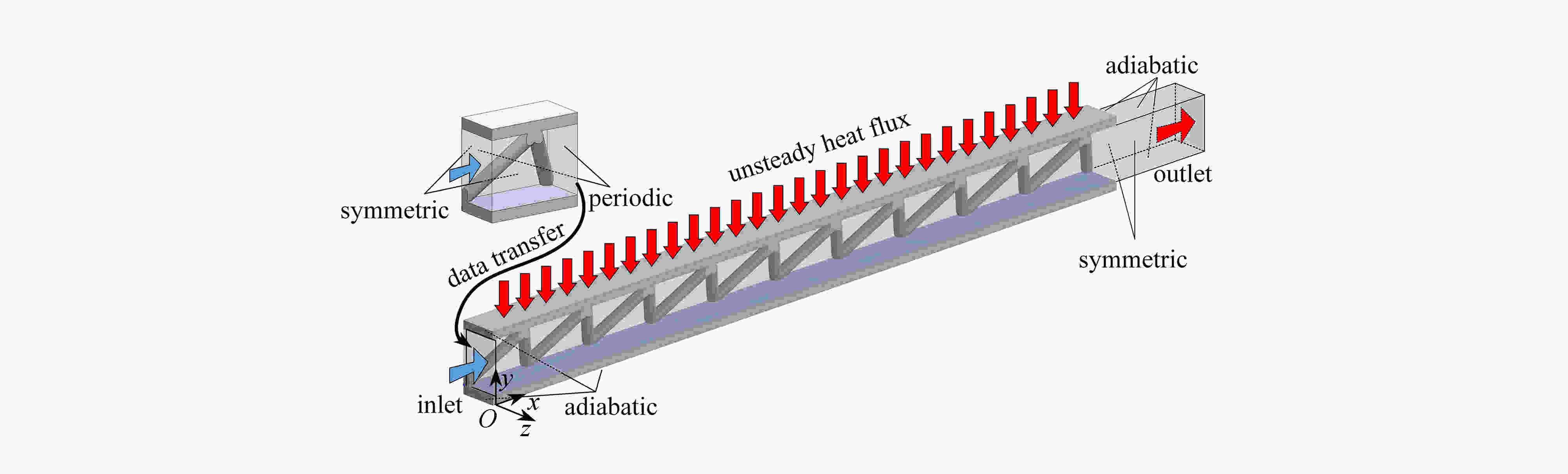
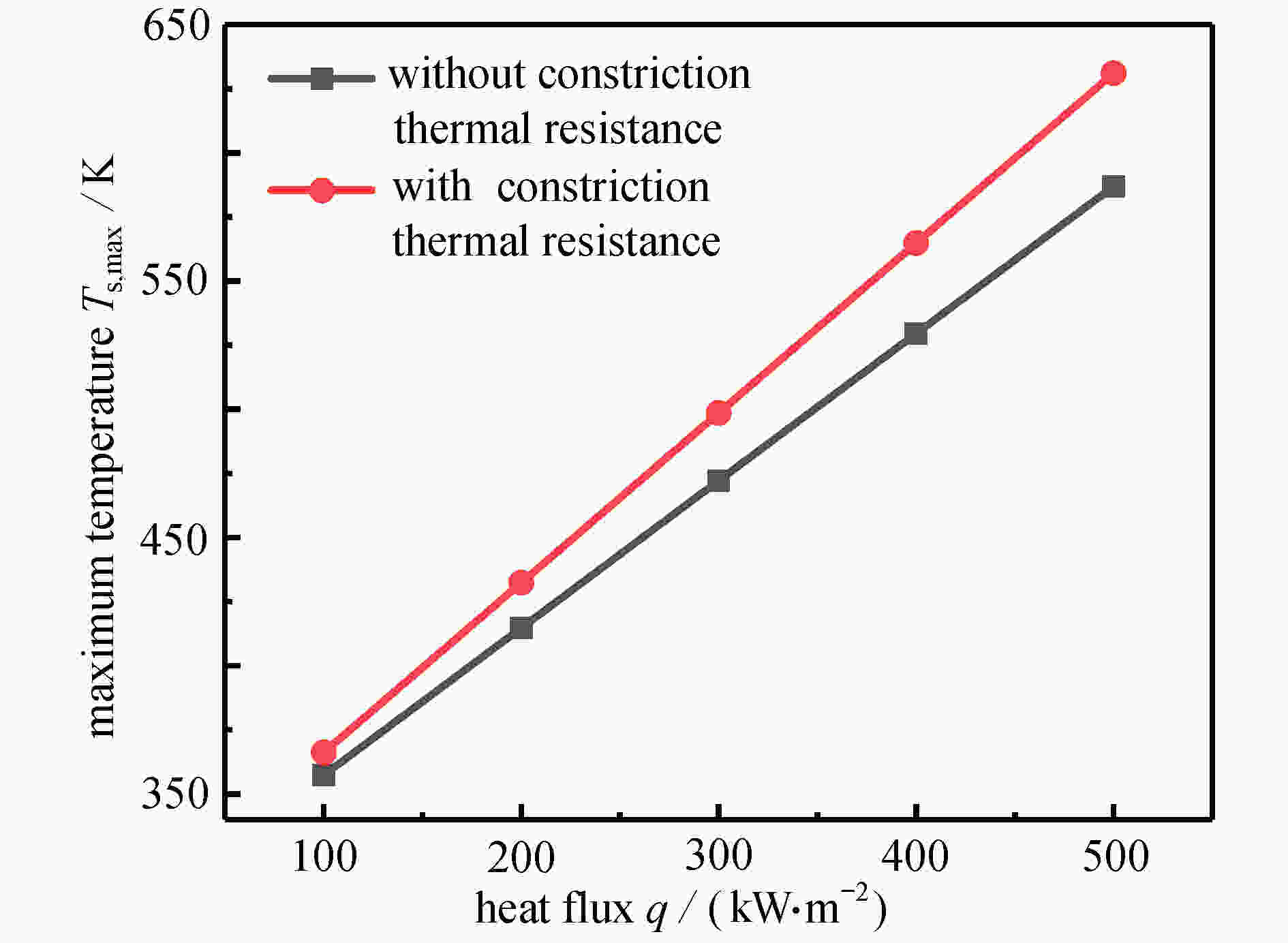
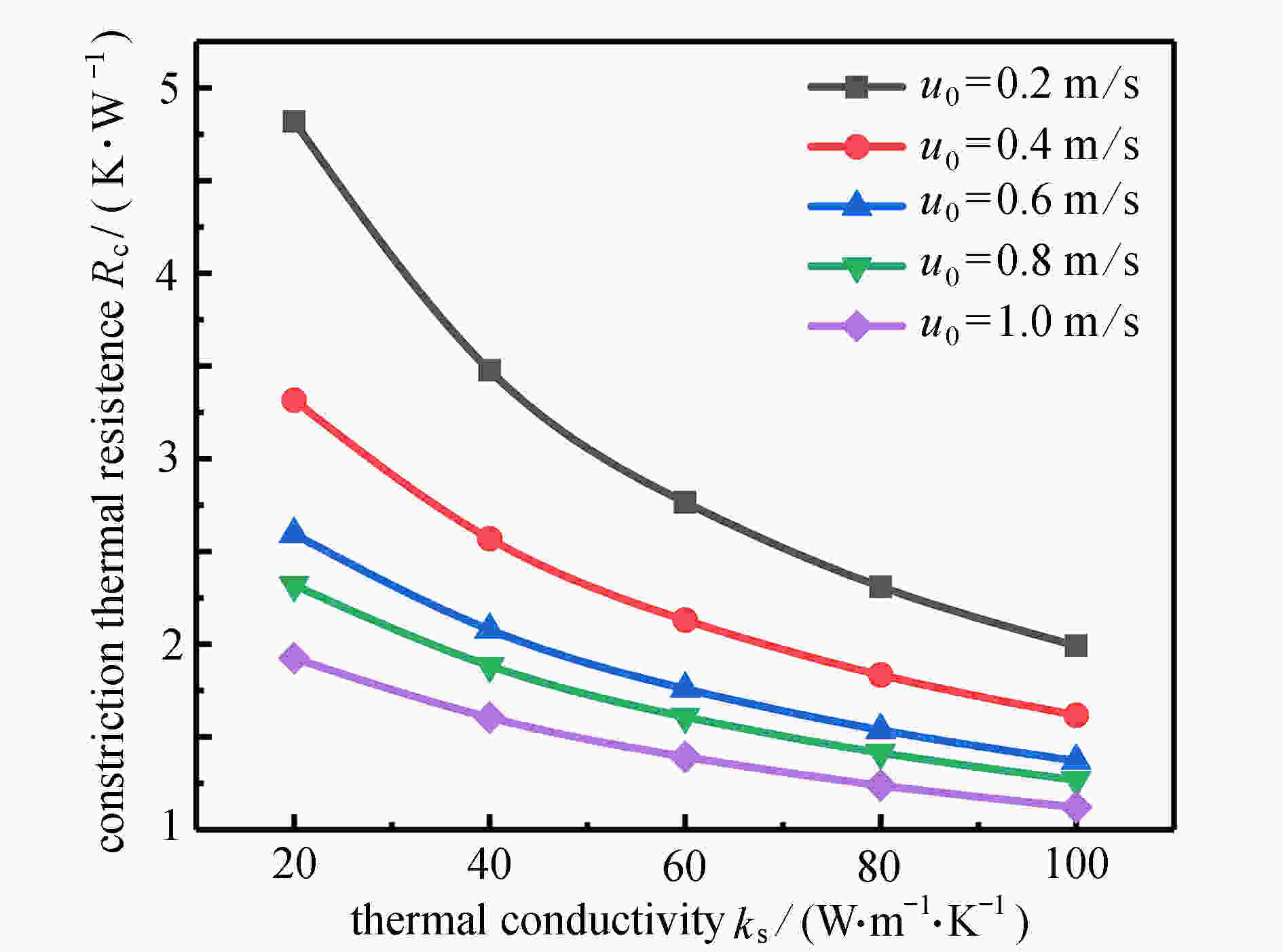
Abstract:Aimed at the active thermal protection with lattice sandwich structures, an unsteady heat transfer theoretical model coupling facesheet and core heat conduction with coolant convection in the sandwich structure, was established. The model equations were discretized with the finite volume method and solved iteratively in MATLAB; the constriction thermal resistance between the facesheet and the lattice struts was considered for the first time in the model, and the approximate analytical solution of the constriction thermal resistance was obtained with the variable separation method; based on the unit-cell model and periodic boundary conditions, heat transfer coefficients hb and hfin required by the model were first obtained through numerical simulation. Finally, a case study with a multi-cell structure was carried out to compare the numerical and theoretical results, and the influence of the constriction thermal resistance on the prediction accuracy was discussed. The results show that, the theoretical model can accurately predict the temperature variations of the sandwich structure and the internal fluid, and the maximum deviation between theory and simulation is less than 1%. As the external heat flux increases, the error of theoretical prediction rises with the constriction thermal resistance ignored. Compared with the numerical simulation, the theoretical model can significantly reduce the calculation time and save calculation resources, thus it is especially suitable for active cooling lattice sandwich structures subjected to complex, non-uniform and unsteady thermal loads.
-
图 1 金字塔型点阵金属夹芯结构的强制对流换热示意图
Figure 1. Schematic of forced convection heat transfer through the pyramidal lattice metal sandwich structure
图 2 点阵夹层结构及内部流体的离散示意图
Figure 2. Discretization of the lattice sandwich structure with internal fluid
图 3 周期性流动传热数值模拟：(a) 计算域及边界条件；(b) 网格
Figure 3. Numerical simulation of periodic flow and heat transfer: (a) the computational domain and boundary conditions; (b) the mesh
图 4 不同Red下，夹芯杆表面的对流换热系数
Figure 4. Heat transfer coefficients on the surface of lattice struts under different Red values
图 5 求解收缩热阻的等效模型
Figure 5. The equivalent model for solving the constriction thermal resistance
图 6 含多个单胞点阵夹层结构数值模拟计算域及边界条件
Figure 6. The numerical simulation domain and boundary conditions for the multi-cell lattice sandwich structure
图 7 加热面平均温度随网格数量的变化曲线
Figure 7. The variation of the average temperature of heating surface with the number of meshes
图 8 RLV再入过程中表面的入射热通量随时间的变化曲线
Figure 8. The incident heat flux profile vs. the re-entry time on the RLV surface
图 9 结构最大温度与流体出口温度的变化曲线：(a) 结构最大温度；(b) 流体出口温度
Figure 9. Variations of the maximum temperature of the sandwich structure and the outlet fluid temperature with time: (a) the maximum temperature of the sandwich structure; (b) the outlet fluid temperature
图 10 不同热流密度下结构的最大温度
Figure 10. The maximum temperature of the structure under different heat flux densities
图 11 不同流体进口速度下收缩热阻随导热率的变化曲线
Figure 11. Variations of the constriction thermal resistance with the thermal conductivity under different inlet fluid velocities
-
[1] 卢天健, 何德坪, 陈常青, 等. 超轻多孔金属材料的多功能特性及应用[J]. 力学进展, 2006, 36(4): 517-535. (LU Tianjian, HE Deping, CHEN Changqing, et al. The multi-functionality of ultra-light porous metals and their applications[J]. Advances in Mechanics, 2006, 36(4): 517-535.(in Chinese) doi: 10.3321/j.issn:1000-0992.2006.04.004 [2] 陈东, 吴永鹏, 李忠盛, 等. 轻质高强多功能点阵夹层结构研究进展[J]. 装备环境工程, 2020, 17(4): 77-84. (CHEN Dong, WU Yongpeng, LI Zhongsheg, et al. Research progress of light weight, high strength and multi-function lattice sandwich structure[J]. Equipment Environmental Engineering, 2020, 17(4): 77-84.(in Chinese) [3] PAN C, HAN Y, LU J. Design and optimization of lattice structures: a review[J]. Applied Sciences, 2020, 10(18): 6374. doi: 10.3390/app10186374 [4] FERRARI L, BARBATO M, ESSER B, et al. Sandwich structured ceramic matrix composites with periodic cellular ceramic cores: an active cooled thermal protection for space vehicles[J]. Composite Structures, 2016, 154: 61-68. doi: 10.1016/j.compstruct.2016.07.043 [5] SONG J, SUN B. Coupled numerical simulation of combustion and regenerative cooling in LOX/methane rocket engines[J]. Applied Thermal Engineering, 2016, 106: 762-773. doi: 10.1016/j.applthermaleng.2016.05.130 [6] FENG S S, LI M Z, JOO J H, et al. Thermomechanical properties of brazed wire-woven bulk Kagome cellular metals for multifunctional applications[J]. Journal of Thermophysics and Heat Transfer, 2012, 26(1): 66-74. doi: 10.2514/1.49434 [7] WADLEY H N G. Multifunctional periodic cellular metals[J]. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2006, 364(1838): 31-68. doi: 10.1098/rsta.2005.1697 [8] KIM T, ZHAO C Y, LU T J, et al. Convective heat dissipation with lattice-frame materials[J]. Mechanics of Materials, 2004, 36(8): 767-780. doi: 10.1016/j.mechmat.2003.07.001 [9] LU T J, VALDEVIT L, EVANS A G. Active cooling by metallic sandwich structures with periodic cores[J]. Progress in Materials Science, 2005, 50(7): 789-815. doi: 10.1016/j.pmatsci.2005.03.001 [10] YAN H, ZHANG Q, CHEN W, et al. An X-lattice cored rectangular honeycomb with enhanced convective heat transfer performance[J]. Applied Thermal Engineering, 2020, 166: 114687. doi: 10.1016/j.applthermaleng.2019.114687 [11] YAN H B, ZHANG Q C, LU T J, et al. A lightweight X-type metallic lattice in single-phase forced convection[J]. International Journal of Heat and Mass Transfer, 2015, 83: 273-283. doi: 10.1016/j.ijheatmasstransfer.2014.11.061 [12] TAKARAZAWA S, USHIJIMA K, FLEISCHHAUER R, et al. Heat-transfer and pressure drop characteristics of micro-lattice materials fabricated by selective laser metal melting technology[J]. Heat and Mass Transfer, 2022, 58: 125-141. doi: 10.1007/s00231-021-03083-0 [13] 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001.TAO Wenquan. Numerical Heat Transfer[M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2001.(in Chinese) [14] MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, Heat and Mass Transfer, 2003, 4(1): 625-632. [15] ŽUKAUSKAS A. Heat transfer from tubes in crossflow[J]. Advances in Heat Transfer, 1972, 8: 93-160. [16] MUZYCHKA Y S, SRIDHAR M R, YOVANOVICH M M, et al. Thermal spreading resistance in multilayered contacts: applications in thermal contact resistance[J]. Journal of Thermophysics and Heat Transfer, 1999, 13(4): 489-494. doi: 10.2514/2.6466 [17] HUANG M J, SHAW Y R, CHIEN H C. Thermal spreading resistance of heat sources on rectangular flux channel under non-uniform convective cooling[J]. International Journal of Thermal Sciences, 2019, 145: 105979. doi: 10.1016/j.ijthermalsci.2019.105979 [18] HE Y R, WANG X Z, HAN J C, et al. Numerical investigation on actively cooled thermal protection systems with Ni-based alloys[J]. Journal of Propulsion and Power, 2014, 30(3): 604-616. doi: 10.2514/1.B34676 [19] KUMAR S, MAHULIKAR S P. Reconstruction of aero-thermal heating and thermal protection material response of a reusable launch vehicle using inverse method[J]. Applied Thermal Engineering, 2016, 103: 344-355. doi: 10.1016/j.applthermaleng.2016.04.100 -
下载:
计量
- 文章访问数: 1129
- HTML全文浏览量: 369
- PDF下载量: 121
- 被引次数: 0
渝公网安备50010802005915号