Dynamic Analysis of the Network Epidemic Model Based on White Noise
-
摘要:
该文基于确定性网络传染病模型, 建立了白噪声影响下的随机网络传染病模型, 证明了模型全局解的存在唯一性, 利用随机微分方程理论得到了传染病随机灭绝和随机持久的充分条件。结果表明, 白噪声对网络传染病传播动力学有很大的影响, 白噪声能有效抑制传染病的传播, 大的白噪声甚至能让原本持久的传染病变得灭绝。最后, 通过数值模拟验证了理论结果。
Abstract:Based on the deterministic network infectious disease model, a stochastic network infectious disease model under the influence of white noise was established, and the existence and uniqueness of the global solution to the model were proved. With the theory of stochastic differential equations, sufficient conditions for stochastic extinction and persistence of infectious diseases were obtained. The results show that, white noise has a great impact on the transmission dynamics of network infectious diseases. White noise can effectively suppress the spread of infectious diseases, and large white noise can even make the original persistent infectious diseases become extinct. Finally, the theoretical results were verified through numerical simulations.
-
Key words:
- epidemic model /
- network /
- white noise
-
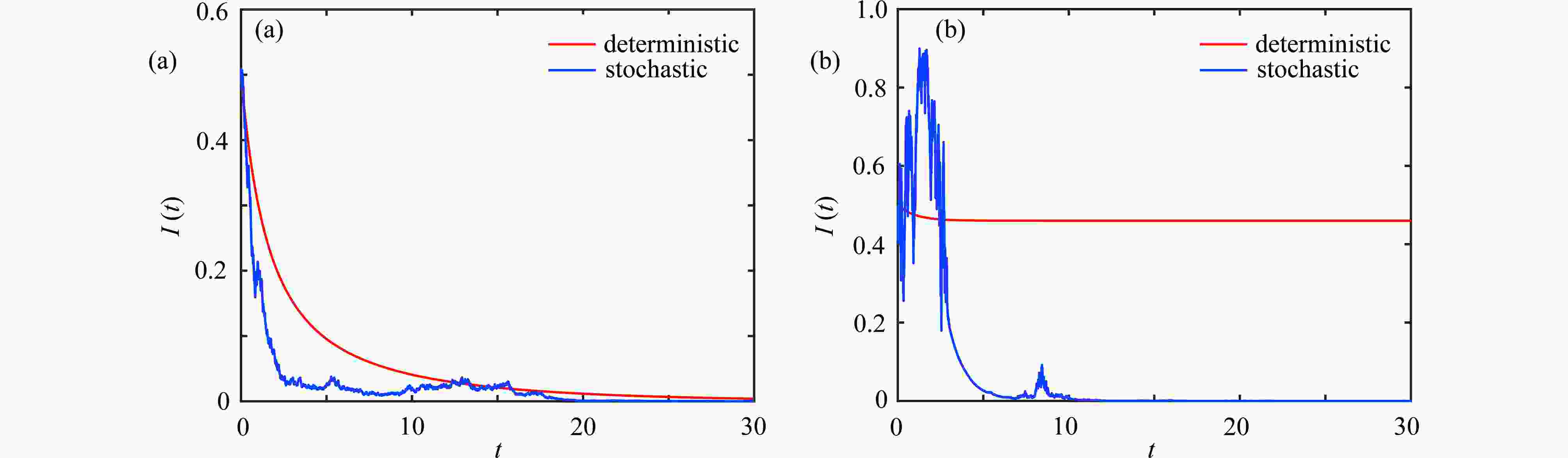
图 2 确定性模型(1)灭绝(持久)情形与随机性模型(2)灭绝情形的I(t)路径模拟:(a) 确定性模型(1)灭绝情形与随机性模型(2)灭绝情形;(b) 确定性模型(1)持久情形与随机性模型(2)灭绝情形
Figure 2. I(t) path simulations of the extinction (persistence) case of deterministic model (1) and the extinction case of stochastic model (2): (a) the extinction case of deterministic model (1) and the extinction case of stochastic model (2); (b) the persistence case of deterministic model (1) and the extinction case of stochastic model (2)
-
[1] 靳祯, 孙桂全, 刘茂省. 网络传染病动力学建模与分析[M]. 北京: 科学出版社, 2014: 1-393.JIN Zhen, SUN Guiquan, LIU Maoxing. Dynamic Modeling and Analysis of Network Infectious Diseases[M]. Beijing: Science Press, 2014: 1-393. (in Chinese) [2] PASTOR-SATORRAS R, VESPIGNANI A. Epidemic spreading in scale-free networks[J]. Physical Review Letters, 2001, 86(14): 3200-3203. [3] WANG L, DAI G Z. Global stability of virus spreading in complex heterogeneous networks[J]. SIAM Journal on Applied Mathematics, 2008, 68(5): 1495-1502. [4] CAO X C, JIN Z. N-intertwined SIS epidemic model with Markovian switching[J]. Stochastics and Dynamics, 2018, 19(4): 1950031. [5] CAO X C, JIN Z. Epidemic threshold and ergodicity of an SIS model in switched networks[J]. Journal of Mathematical Analysis and Applications, 2019, 479(1): 1182-1194. [6] CAO X C, JIN Z, LIU G R, et al. On the basic reproduction number in semi-Markov switching networks[J]. Journal of Biological Dynamics, 2021, 15(1): 73-85. [7] 曹娟, 任凤丽. Markov切换时滞基因调控网络的均方同步和随机无源同步[J]. 应用数学和力学, 2022, 43(2): 198-206. (CAO Juan, REN Fengli. Mean-square synchronization and stochastically passive synchronization of delayed gene regulatory networks with Markovian switching[J]. Applied Mathematics and Mechanics, 2022, 43(2): 198-206.(in Chinese)CAO Juan, REN Fengli. Mean-square synchronization and stochastically passive synchronization of delayed gene regulatory networks with Markovian switching[J]. Applied Mathematics and Mechanics, 2022, 43(2): 198-206. (in Chinese) [8] 何雪晴, 韦煜明. 同时具有logistic 出生和Markov切换的随机SIRS传染病模型的动力学[J]. 应用数学和力学, 2021, 42(12): 1327-1337. (HE Xueqing, WEI Yuming. Dynamics of a class of stochastic SIRS infectious disease models with both logistic birth and Markov switching[J]. Applied Mathematics and Mechanics, 2021, 42(12): 1327-1337.(in Chinese)HE Xueqing, WEI Yuming. Dynamics of a class of stochastic SIRS infectious disease models with both logistic birth and Markov switching[J]. Applied Mathematics and Mechanics, 2021, 42(12): 1327-1337. (in Chinese) [9] 张丽娟, 王福昌, 万永革, 等. 一类潜伏期有传染性的传染病模型动力学分析[J]. 应用数学和力学, 2021, 42(8): 866-873. (ZHANG Lijuan, WANG Fuchang, WAN Yongge, et al. Dynamic analysis of an epidemic model with infectivity in the incubation period[J]. Applied Mathematics and Mechanics, 2021, 42(8): 866-873.(in Chinese)ZHANG Lijuan, WANG Fuchang, WAN Yongge, et al. Dynamic analysis of an epidemic model with infectivity in the incubation period[J]. Applied Mathematics and Mechanics, 2021, 42(8): 866-873. (in Chinese) [10] GRAY A, GREENHALGH D, HU L, et al. A stochastic differential equation SIS epidemic model[J]. SIAM Journal on Applied Mathematics, 2011, 71(3): 876-902. [11] LIN Y G, JIANG D Q, WANG S A. Stationary distribution of a stochastic SIS epidemic model with vaccination[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 394: 187-197. [12] MIAO A Q, ZHANG J, ZHANG T Q, et al. Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination[J]. Computational and Mathematical Methods in Medicine, 2017, 2017(2): 1-10. [13] CHANG Z B, MENG X Z, LU X. Analysis of a novel stochastic SIRS epidemic model with two different saturated incidence rates[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 472: 103-116. [14] ØKSENDAL B. Stochastic Differential Equations and Applications[M]. New York: Springer-Verlag Heidelberg Press, 2000: 1-332. [15] MAO X R. Stochastic Differential Equations and Applications[M]. Cambridge: Woodhead Publishing Limited Press, 2011: 1-422. [16] LI X Y, GRAY A, JIANG D Q, et al. Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching[J]. Journal of Mathematical Analysis and Applications, 2011, 376(1): 11-28. -





 下载:
下载:


 渝公网安备50010802005915号
渝公网安备50010802005915号