Multimaterial Lattice Structures With Thermally Programmable Mechanical Behaviors
-
摘要:
传统的点阵结构一旦制备完成,其力学性能通常在使用寿命内保持不变。设计和制造具有环境适应特性的智能点阵结构,可编程地感知和响应外界变化(例如光强、压强、溶液、温度、电磁场、电化学激励),并在时间和空间上进行形状重构、模式转换和性能调控,仍然是人造材料研究领域重要的科学挑战。该文采用具有不同玻璃化转变温度和温度依赖性的多种聚合物材料,通过合理设计材料空间分布,提出了一类具有热可编程力学响应能力的多材料点阵结构。结合理论分析和有限元模拟,研究了组分材料相对刚度对多材料点阵结构的Poisson比、变形模式以及结构稳定性的影响。通过温度变化实现了对多材料点阵结构弹性常数、压溃响应和结构稳定性的调控,使多材料点阵结构表现出极大的热变形、超弹性和形状记忆效应。为设计和制造自适应保护装备、生物医学设备、航空航天领域的变形结构、柔性电子设备、自组装结构和可变形软体机器人等开辟了新途径。
Abstract:Traditional lattice structures usually maintain their mechanical properties throughout their lifetime. Designing and manufacturing intelligent materials with environmental adaptability, programmable sense and responses to external changes (such as light, pressure, solution, temperature, electromagnetic field and electrochemical reaction), shape transformation, mode conversion and performance regulation in space and time, are still important scientific challenges in the field of artificial materials. In this paper, multimaterial lattice structures with thermally programmable mechanical responses were proposed by means of polymer materials with disparate glass transition temperatures and temperature dependencies, and through reasonable design of the spatial distribution of the materials. By theoretical analysis combined with finite element simulation, the effects of the relative stiffnesses of constitute materials on Poisson’s ratios, deformation modes and structural stability of the multimaterial lattice structures, were studied. The elastic constants, crushing responses and structural stability of multimaterial lattice structures were regulated by temperature control, consequently the multimaterial lattice structures were endowed with giant thermal deformation, hyperelasticity and shape memory effects. This paper opens up new avenues for the design and manufacture of adaptive protection equipment, biomedical devices, aerospace morphing structures, flexible electronic devices, self-assembly structures and reconfigurable soft robots.
-
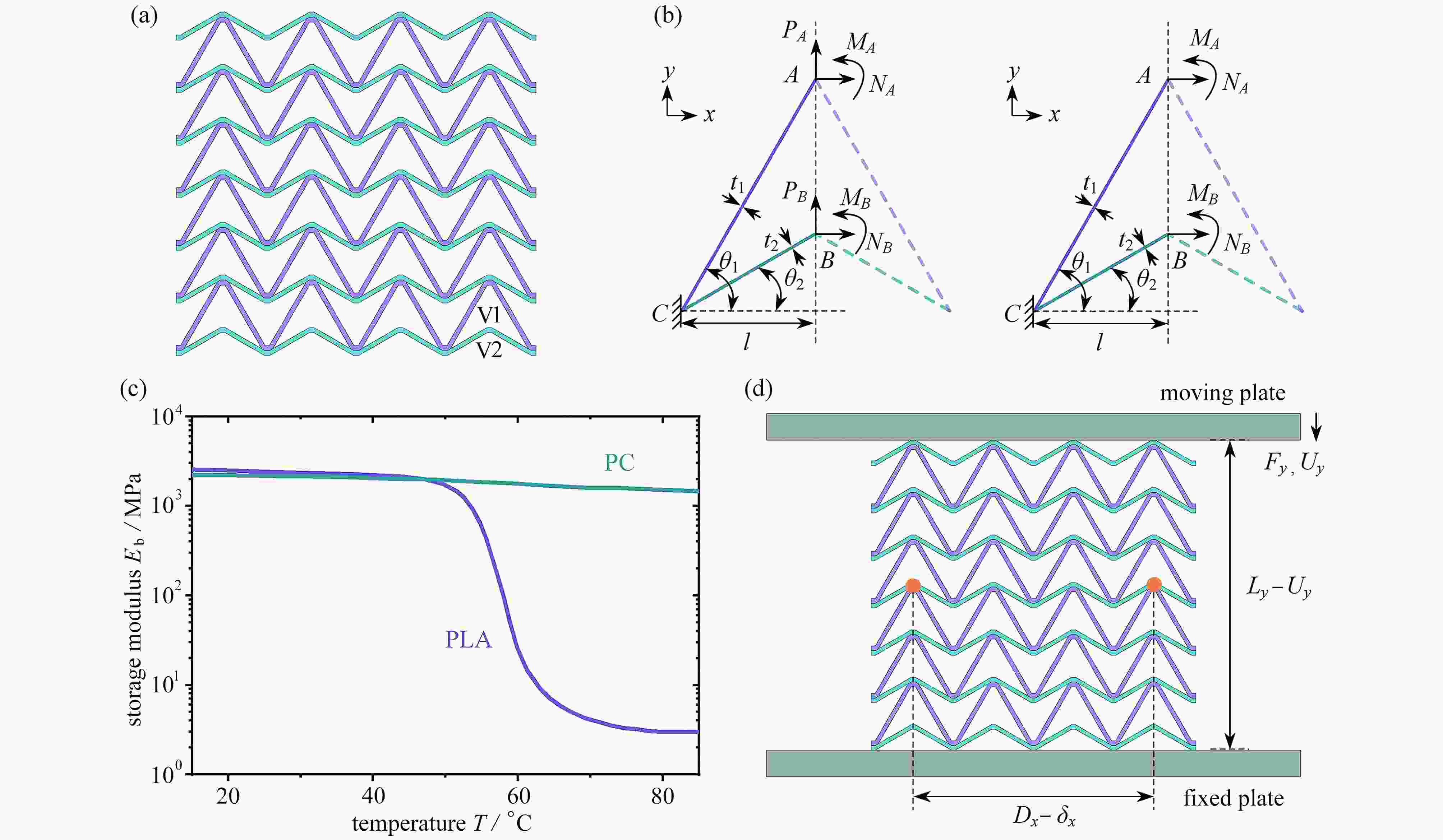
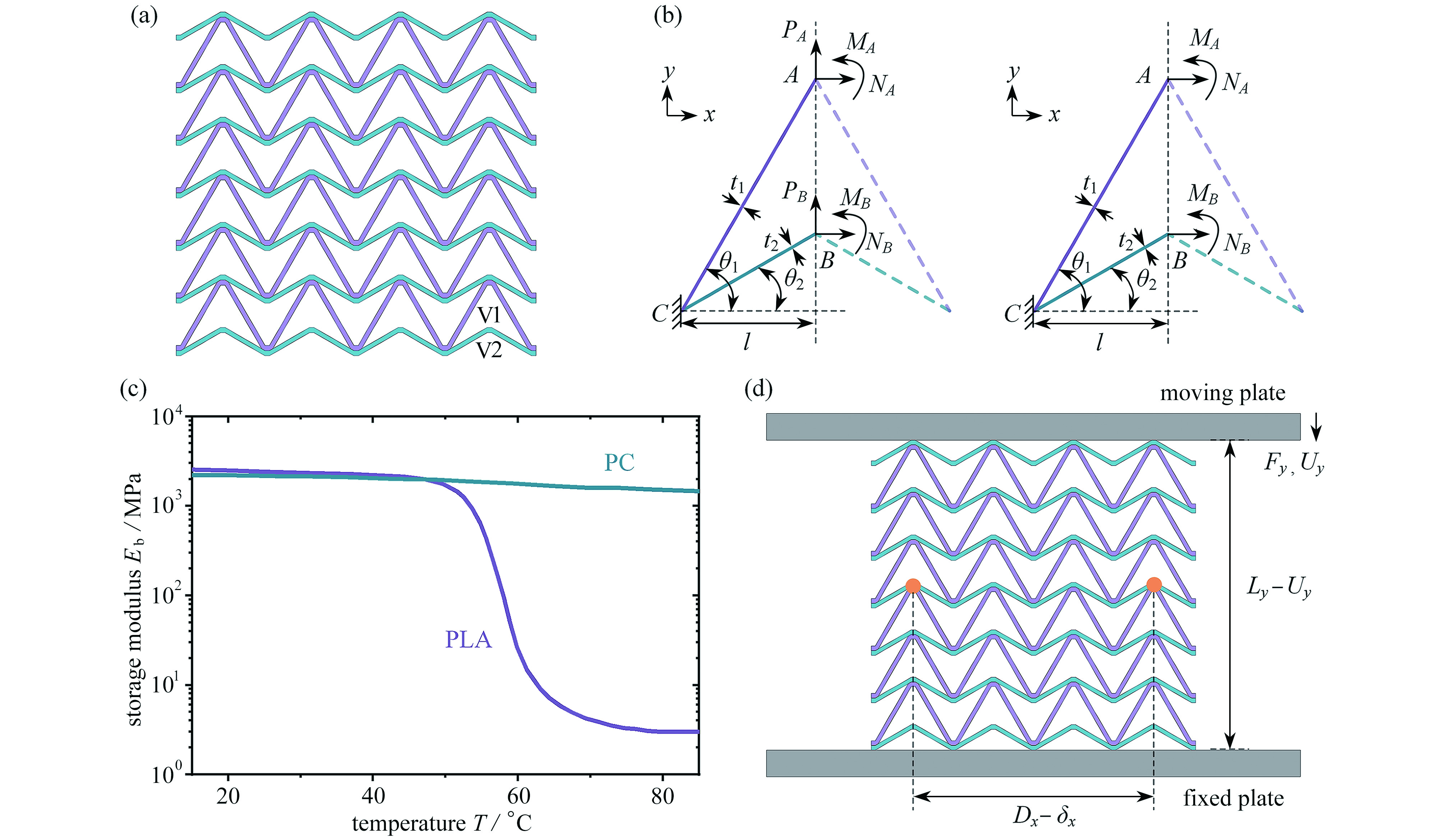
图 1 双材料双V内凹结构:(a) 双材料双V内凹结构示意图;(b) 沿y和x方向分别加载时的边界条件;(c) PLA和PC材料的储能模量与温度的关系;(d) 准静态单轴压缩示意图
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同。
Figure 1. Bimaterial concave double-V structures: (a) schematic diagram of bimaterial concave double-V structures; (b) boundary conditions for loads along y and x directions; (c) storage modulus Eb vs. temperature T for PLA and PC; (d) schematic diagram of quasi-static uniaxial compression
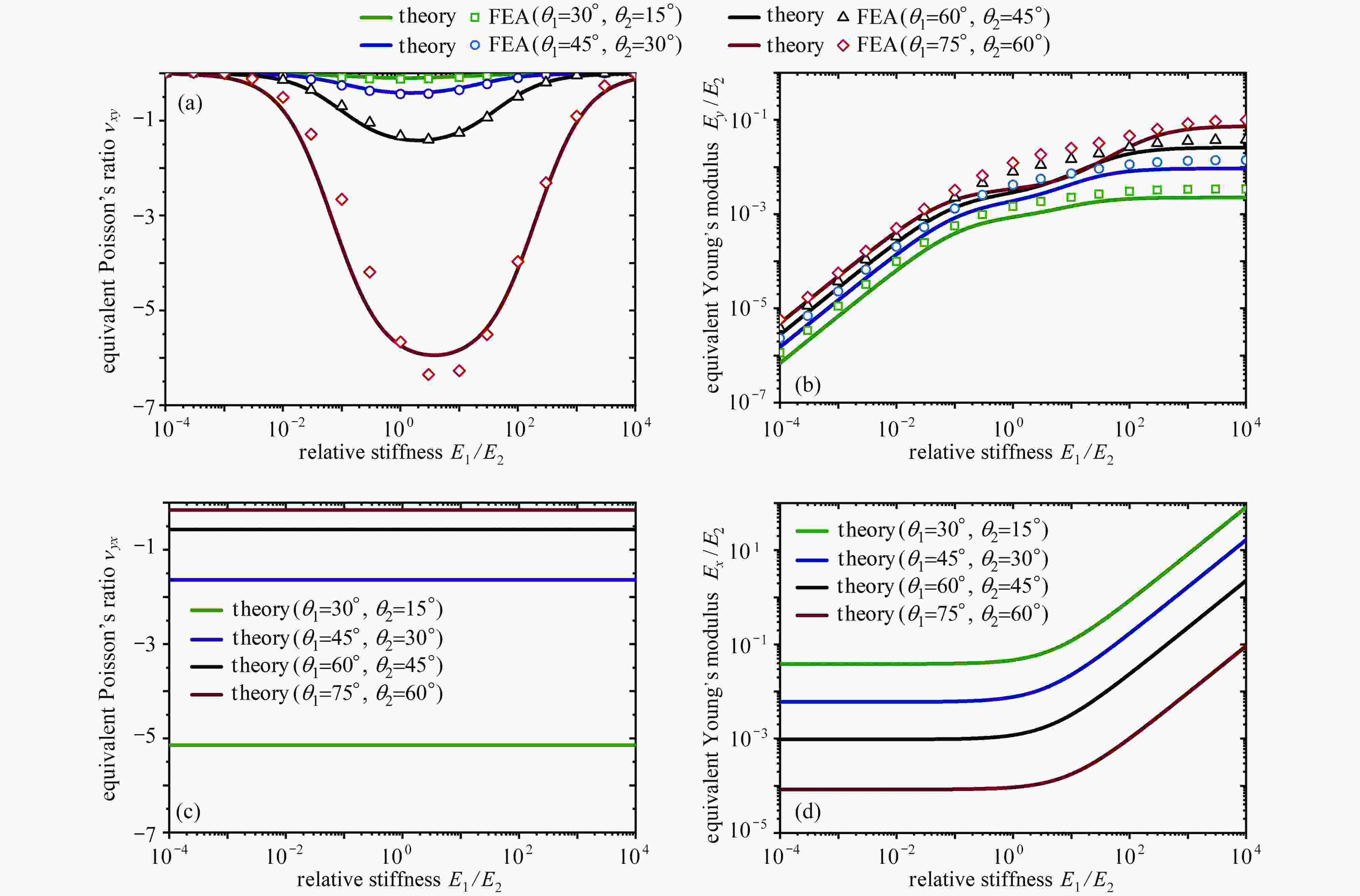
图 2 组分材料相对刚度
${E_1}/{E_2}$ 对双材料双V内凹结构弹性常数的影响:(a) Poisson比${\nu _{xy}}$ 与相对刚度${E_1}/{E_2}$ 的函数关系;(b) 弹性模量${E_y}/{E_2}$ 与相对刚度${E_1}/{E_2}$ 的函数关系;(c) Poisson比${\nu _{yx}}$ 与相对刚度${E_1}/{E_2}$ 的函数关系;(d) 弹性模量${E_x}/{E_2}$ 与相对刚度${E_1}/{E_2}$ 的函数关系Figure 2. The influence of relative stiffness
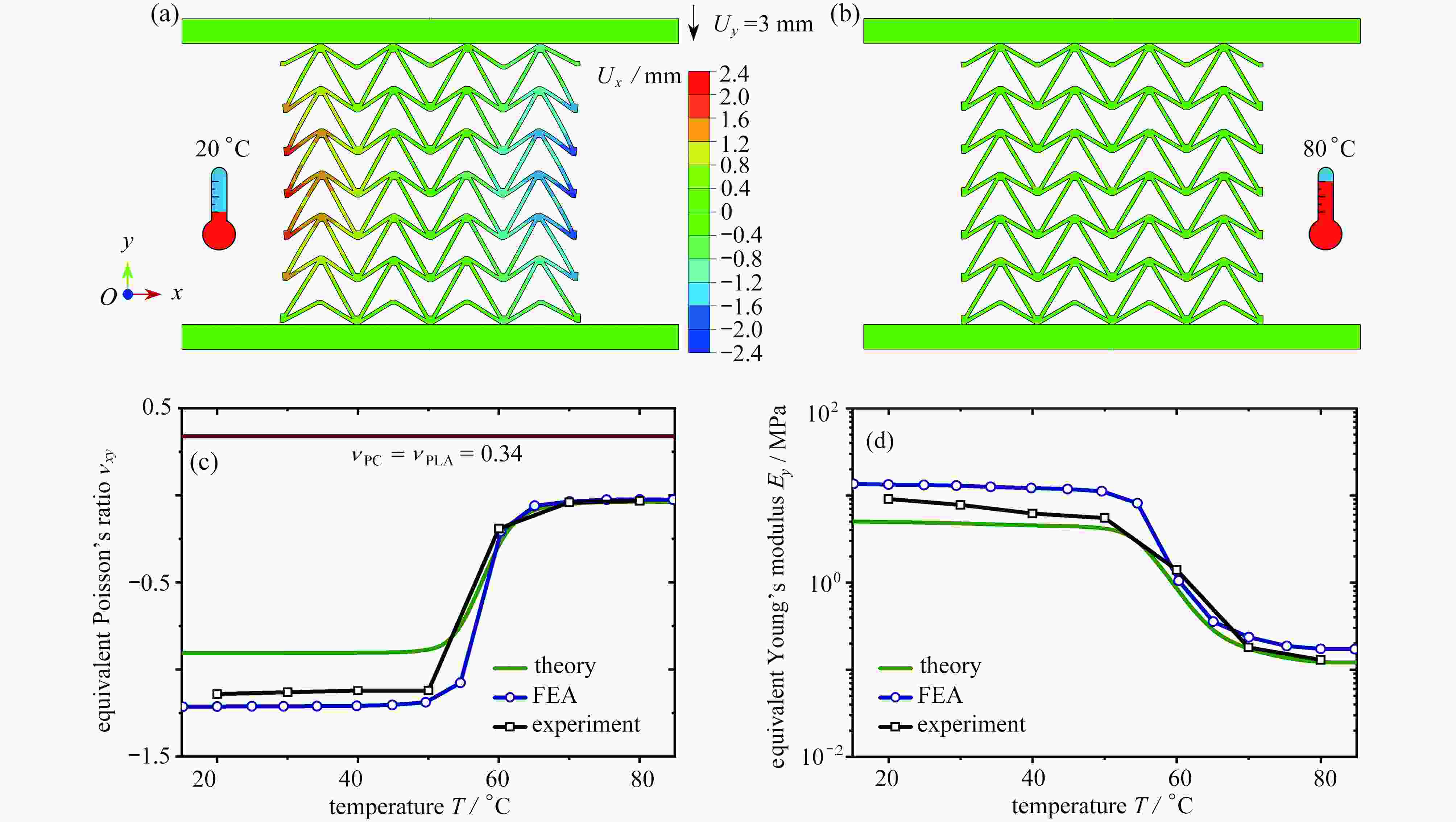
${E_1}/{E_2}$ of the constituent materials on elastic constants of bimaterial double-V structures: (a) equivalent Poisson’s ratio${\nu _{xy}}$ as functions of relative stiffness${E_1}/{E_2}$ ; (b) relative Young’s modulus${E_y}/{E_2}$ as functions of relative stiffness${E_1}/{E_2}$ ; (c) equivalent Poisson’s ratio${\nu _{yx}}$ as functions of relative stiffness${E_1}/{E_2}$ ; (d) relative Young’s modulus${E_x}/{E_2}$ as functions of relative stiffness${E_1}/{E_2}$ 图 3 温度变化对双材料双V内凹结构弹性常数的影响:(a) 低温时双V结构在y方向受压时的横向变形;(b) 高温时双V结构在y方向受压时的横向变形;(c) 不同温度下
${\nu _{xy}}$ 的理论、模拟和实验结果对比;(d) 不同温度下${E_y}$ 的理论、模拟和实验结果对比Figure 3. The influences of temperatures on elastic constants of bimaterial double-V structures: (a) simulated lateral deformation for y-direction load at low temperatures; (b) simulated lateral deformation for y-direction load at high temperatures; (c) theoretical, numerical and experimental results of Poisson’s ratio
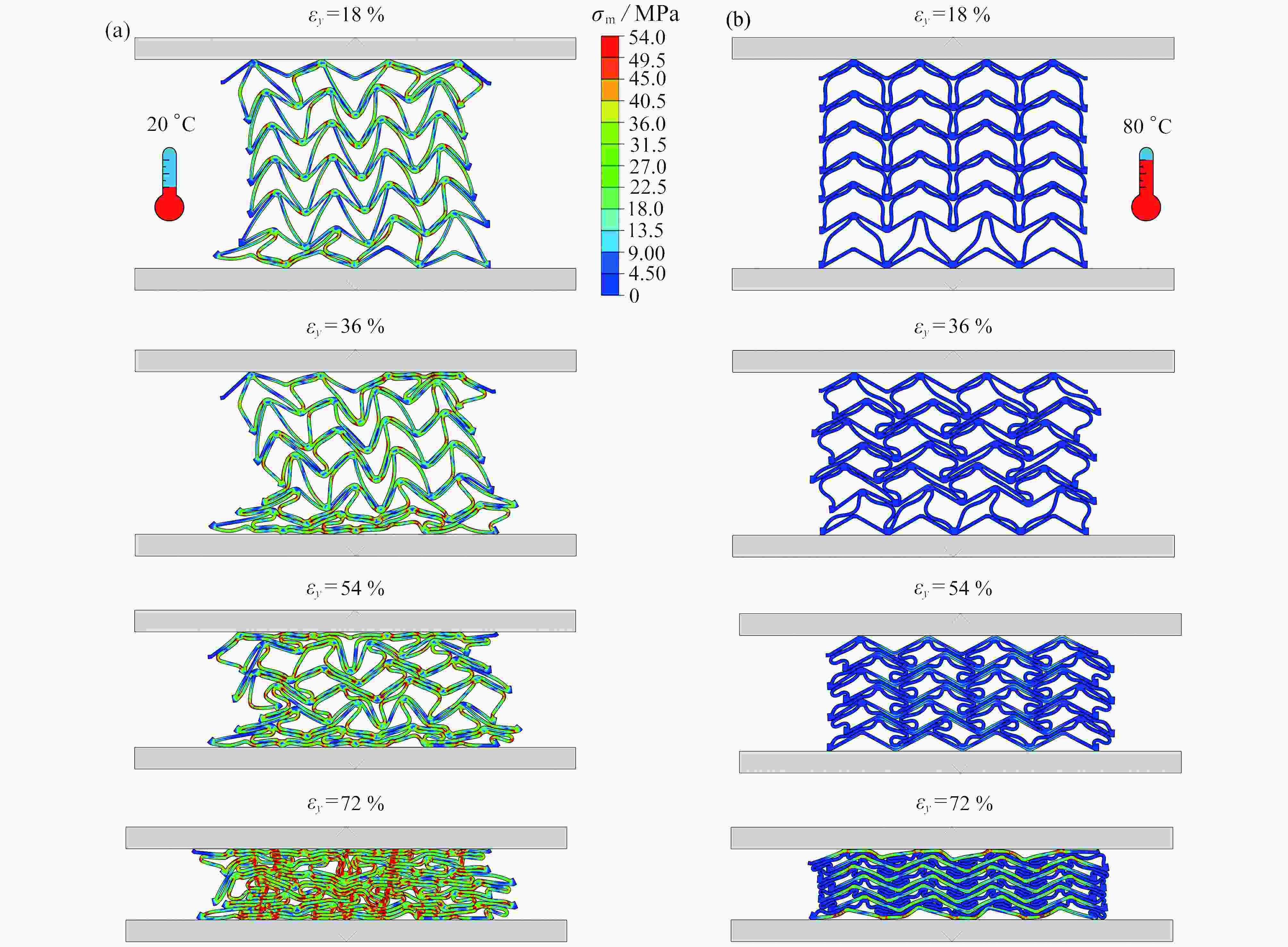
${\nu _{xy}}$ as functions of temperature T; (d) theoretical, numerical and experimental results of Young’s modulus${E_y}$ as functions of temperature T图 4 温度变化对双材料双V结构变形模式的影响:(a) 低温时双V结构在y方向的压溃过程;(b) 高温时双V结构在y方向的压溃过程
Figure 4. The influences of temperatures on deformation modes of bimaterial double-V structures: (a) simulated crushing process for y-direction load at a low temperature; (b) simulated crushing process for y-direction load at a high temperature
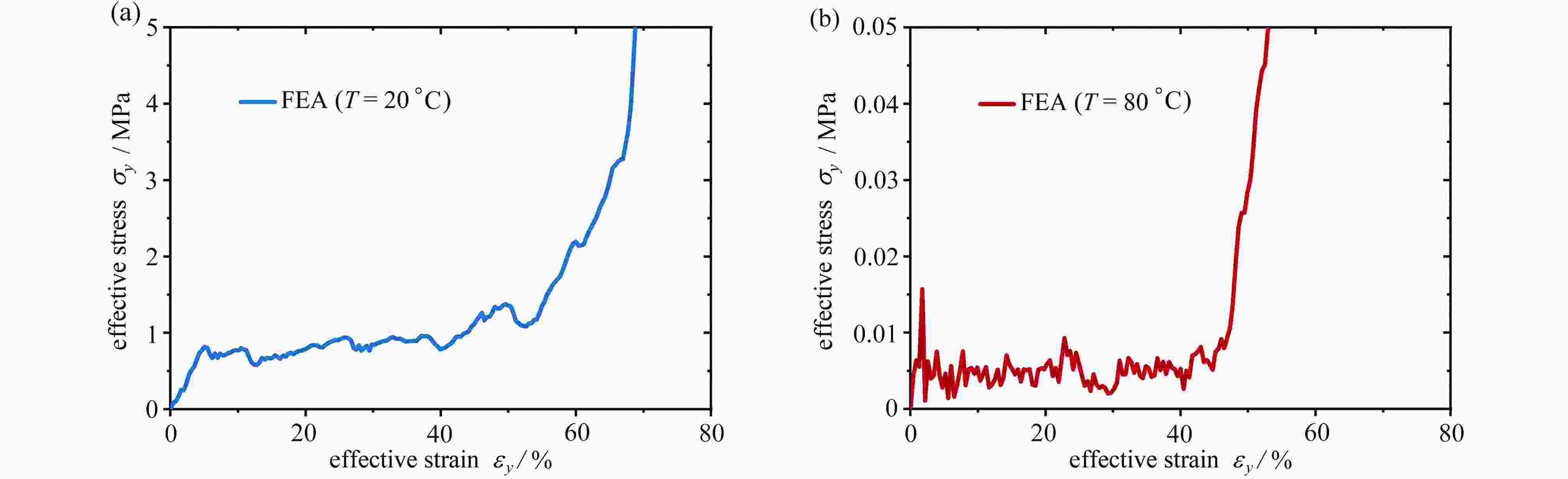
图 5 温度变化对双材料双V结构应力-应变响应的影响:(a) 低温时双V结构在y方向压溃时的应力-应变曲线;(b) 高温时双V结构在y方向压溃时的应力-应变曲线
Figure 5. The influence of temperature on stress-strain response of bimaterial double-V structures: (a) numerical results of stress-strain curve for y-direction load at low temperature; (b) numerical results of stress-strain curve for y-direction load at high temperature
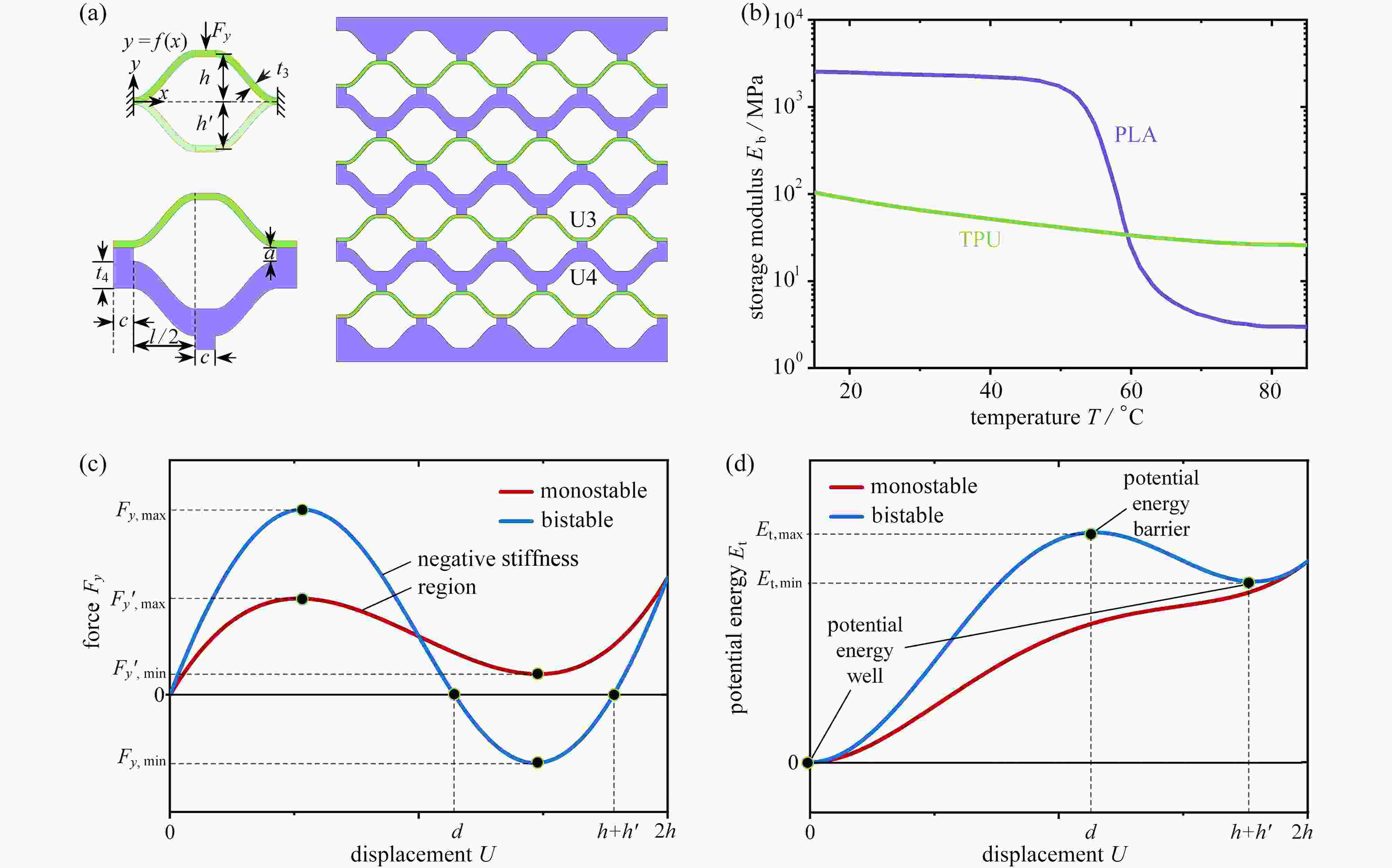
图 6 双材料双U跳变结构:(a) 双材料双U结构及单元几何参数示意图;(b) PLA和TPU材料的储能模量与温度的关系;(c) 单稳态和双稳态单元的力-位移曲线示意图;(d) 单稳态和双稳态单元的势能-位移曲线示意图
Figure 6. Bimaterial double-U snapping structures: (a) schematic diagram of bimaterial double-U structures and geometric parameters of the unit cell; (b) storage modulus Eb vs. temperature T for PLA and TPU; (c) force-displacement curves of the monostable and bistable unit cells; (d) potential energy-displacement curves of the monostable and bistable unit cells
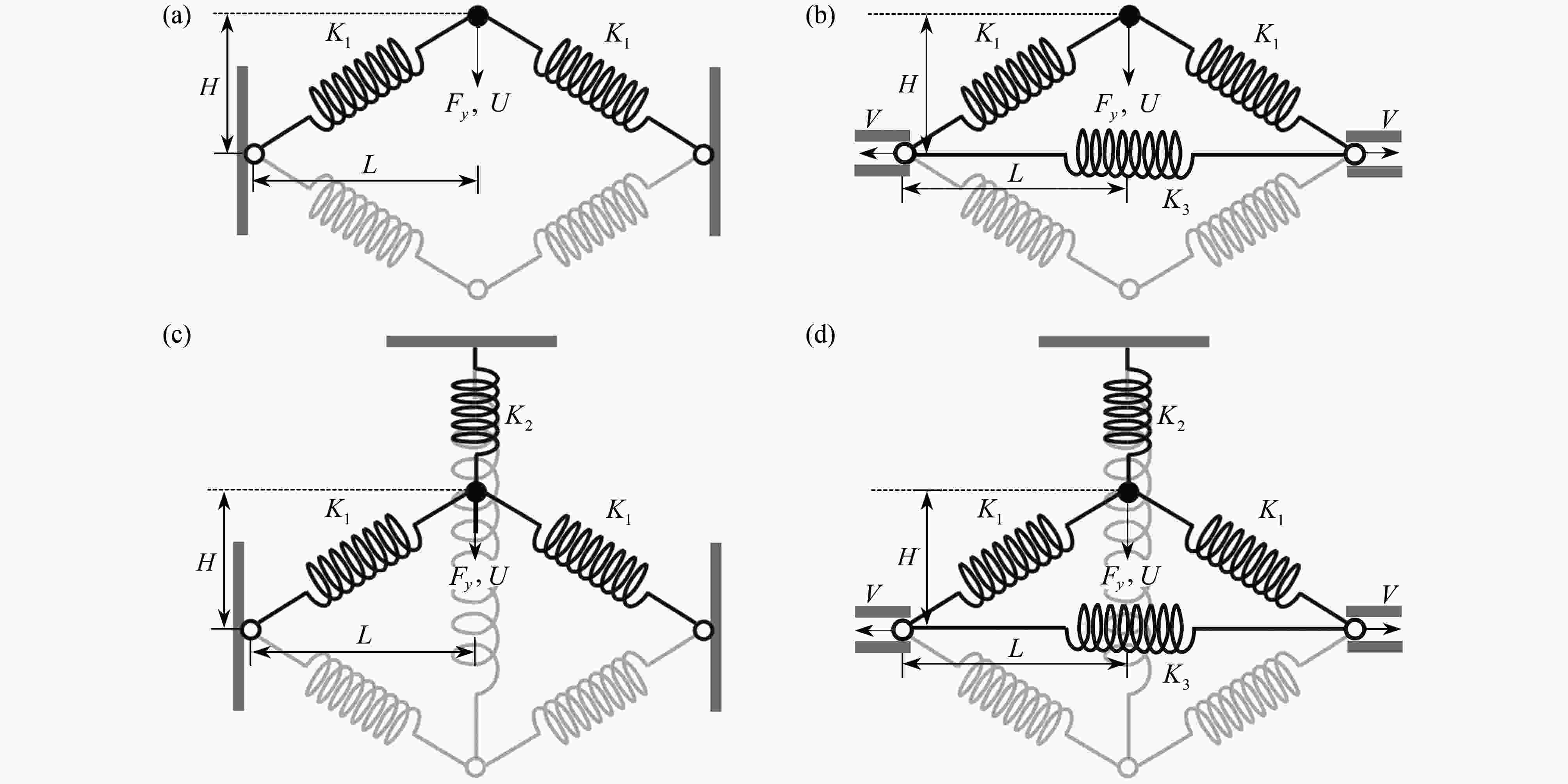
图 7 Von Mises桁架模型的系统稳定性分析:(a) 两端完全约束的对称双稳态系统;(b) 两端不完全约束的对称双稳态系统;(c) 两端完全约束并加上竖直弹簧的非对称双稳态或单稳态系统;(d) 两端不完全约束并加上竖直弹簧的非对称双稳态或单稳态系统
Figure 7. System stability analysis of von Mises truss models: (a) the symmetric bistable system with complete constraints at both ends; (b) the symmetric bistable system with incomplete constraints at both ends; (c) the asymmetric bistable or monostable system with a vertical spring and complete constraints at both ends; (d) the asymmetric bistable or monostable system with a vertical spring and incomplete constraints at both ends
图 8 Von Mises桁架模型的力-位移响应:(a)
${K_3}/{K_1} \to \infty $ 且$H/L = 1$ 时,${K_2}/{K_1}$ 对系统力-位移曲线的影响;(b)${K_2}/{K_1} = 0$ 且$H/L = 1$ 时,${K_3}/{K_1}$ 对系统力-位移曲线的影响;(c)${K_2}/{K_1} = 0.1$ 且$H/L = 1$ 时,${K_3}/{K_1}$ 对系统力-位移曲线的影响;(d)${K_2}/{K_1} = 0.1$ 且${K_3}/{K_1} = 1$ 时,$H/L$ 对系统力-位移曲线的影响Figure 8. The force-displacement responses of von Mises truss models: (a) the influence of
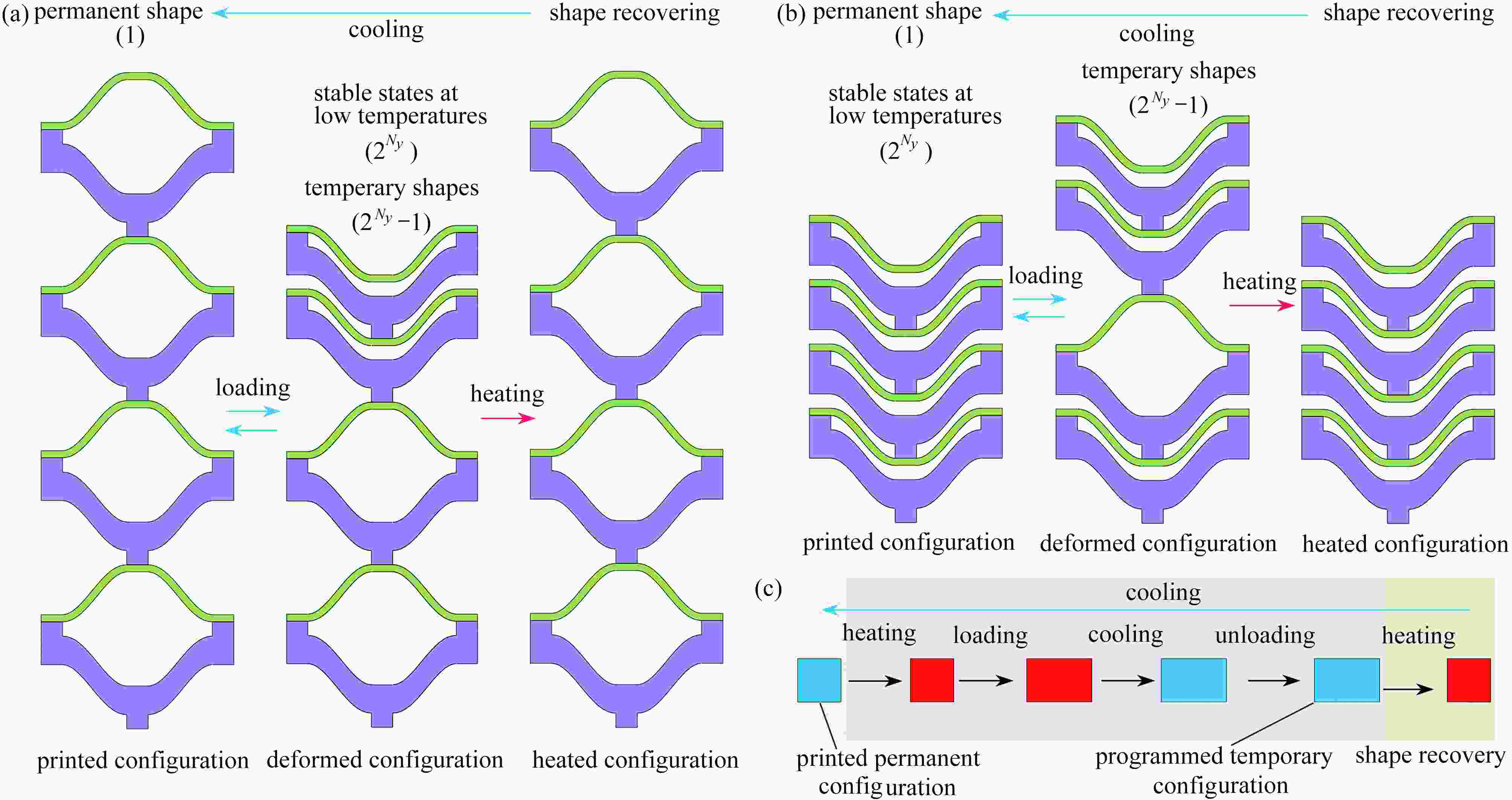
${K_2}/{K_1}$ on the force-displacement curves of the system for${K_3}/{K_1} \to \infty $ and$H/L = 1$ ; (b) the influence of${K_3}/{K_1}$ on the force-displacement curves of the system for${K_2}/{K_1} = 0$ and$H/L = 1$ ; (c) the influence of${K_3}/{K_1}$ on the force-displacement curves of the system for${K_2}/{K_1} = 0.1$ and$H/L = 1$ ; (d) the influence of$H/L$ on the force-displacement curves of the system for${K_2}/{K_1} = 0.1$ and${K_3}/{K_1} = 1$ 图 9 双U结构的形状重构和恢复的实验过程:(a) 初始完全展开的双U结构的形状重构和恢复过程;(b) 初始完全闭合的双U结构的形状重构和恢复过程
Figure 9. Experimental processes of shape reconfiguration and recovery of double-U structures: (a) shape reconfiguration and recovery of initial double-U structure with fully expanded configuration; (b) shape reconfiguration and recovery of initial double-U structure with fully contracted configuration
图 10 双材料双U结构在加热恢复过程中的热变形及热膨胀系数:(a)初始外凸单元加热恢复过程中的正热膨胀变形;(b) 初始内凹单元加热恢复过程中的负热膨胀变形;(c) 双U结构在加热恢复过程中的热膨胀系数与已知文献中的材料和结构的实验结果对比
Figure 10. Thermal deformations and thermal expansion coefficients of bimaterial double-U structures during heating recovery: (a) the positive thermal expansion of an initial convex unit cell during heating recovery; (b) the negative thermal expansion of an initial concave unit cell during heating recovery; (c) the thermal expansion coefficients of bimaterial double-U structures during heating recovery compared with the experimental results of materials and structures reported previously
图 11 不同材料和结构的热力循环
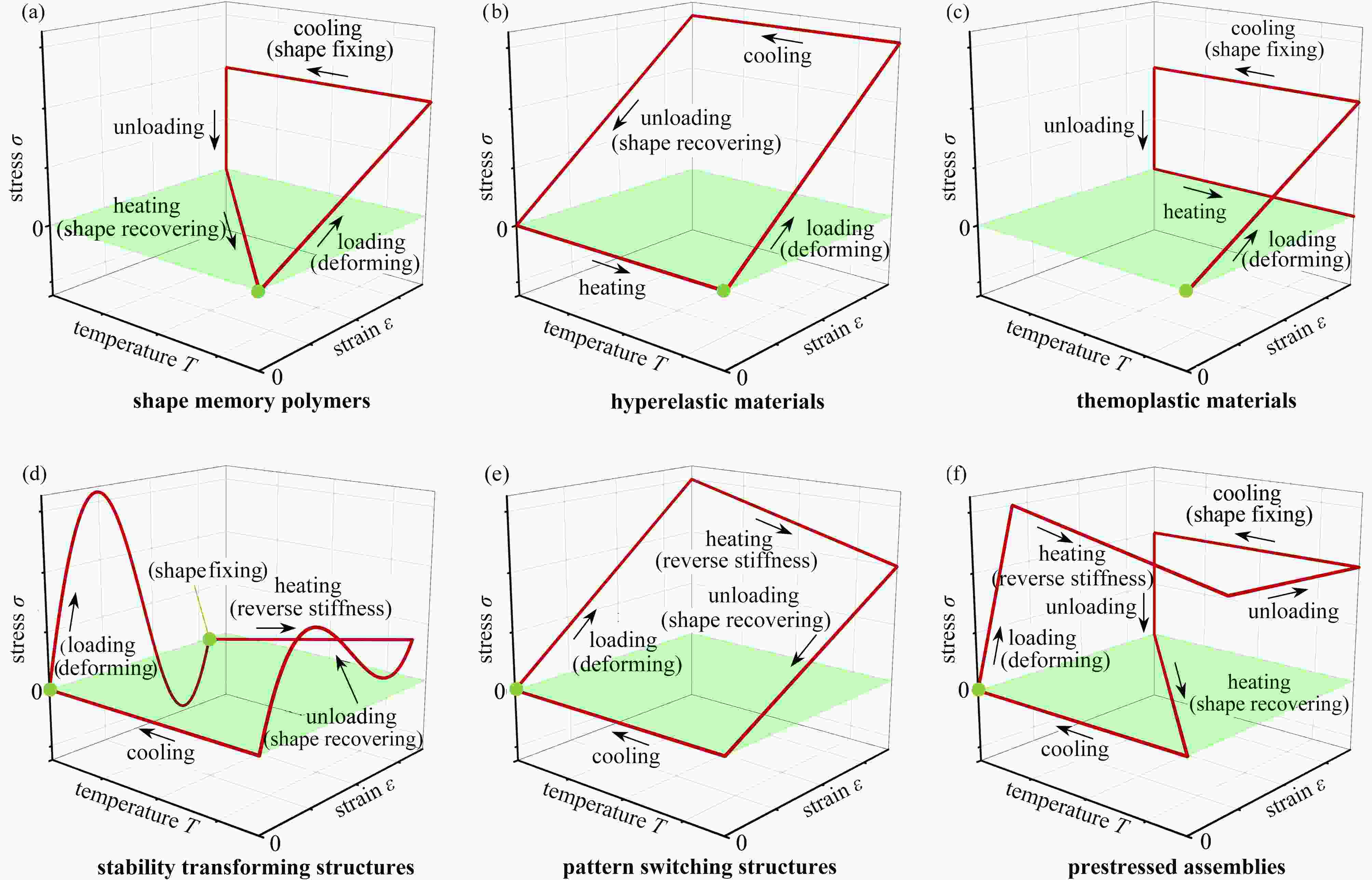
$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图:(a) 形状记忆聚合物$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图[90-94];(b) 超弹性材料$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图;(c) 热塑性材料$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图;(d) 稳定性转换双U结构单元$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图;(e) 模式切换结构$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图[48];(f) 预应力装配体$\varepsilon {\text{-}} T {\text{-}} \sigma$ 示意图[49]Figure 11. The
$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagrams of the thermomechanical cycle for different materials and structures: (a) the$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagram of shape memory polymers[90-94]; (b) the$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagram of hyperelastic materials; (c) the$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagram of themoplastic materials; (d) the$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagram of the unit cell of stability transforming double-U structures; (e) the$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagram of the pattern switching structures[48]; (f) the$\varepsilon {\text{-}} T {\text{-}} \sigma$ diagram of the prestressed assemblies[49]图 12 稳定性转换双U结构的形状重构和变形恢复机制:(a) 初始完全展开的双U结构的形状重构和恢复机制;(b) 初始完全闭合的双U结构的形状重构和恢复机制;(c) 形状记忆聚合物的形状重构和变形恢复机制
Figure 12. The shape reconfiguration and recovery mechanism of the stability transforming double-U structures: (a) the shape reconfiguration and recovery mechanism of initial structures with fully expanded configurations; (b) the shape reconfiguration and recovery mechanism of initial structures with fully contracted configurations; (c) the shape reconfiguration and recovery mechanism of shape memory polymers
表 1 有限元分析中组分材料的性能参数
Table 1. Mechanical properties of constituent materials used in the finite element analysis
material parameter PC PLA temperature T/℃ 20 80 20 80 density ρb/(kg/m3) 1 220 1 220 1 220 1 220 Poisson’s ratio $ {\nu _{\text{b}}} $ 0.34 0.34 0.34 0.34 elastic modulus Eb/MPa 2 207 1 490 2 517 3 yield strength σb/MPa 54 22 50 2 yield strain εb/% 4.3 2.5 3.3 5.2 -
[1] SCHAEDLER T A, JACOBSEN A J, TORRENTS A, et al. Ultralight metallic microlattices[J]. Science, 2011, 334(6058): 962-965. doi: 10.1126/science.1211649 [2] ZHENG X, LEE H, WEISGRABER T H, et al. Ultralight, ultrastiff mechanical metamaterials[J]. Science, 2011, 334(6190): 1373-1377. [3] MEZA L R, DAS S, GREER J R. Strong, lightweight, and recoverable three-dimensional ceramic nanolattices[J]. Science, 2014, 345(6202): 1322-1326. doi: 10.1126/science.1255908 [4] MEZA L R, ZELHOFER A J, CLARKE N, et al. Resilient 3D hierarchical architected metamaterials[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(37): 11502-11507. doi: 10.1073/pnas.1509120112 [5] ZHENG X, SMITH W, JACKSON J, et al. Multiscale metallic metamaterials[J]. Nature Materials, 2016, 15: 1100-1106. doi: 10.1038/nmat4694 [6] TANCOGNE-DEJEAN T, DIAMANTOPOULOU M, GORJI M B, et al. 3D plate-lattices: an emerging class of low-density metamaterial exhibiting optimal isotropic stiffness[J]. Advanced Materials, 2018, 30(45): 1803334. doi: 10.1002/adma.201803334 [7] BERGER J B, WADLEY H N G, MCMEEKING R M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness[J]. Nature, 2017, 543: 533-537. doi: 10.1038/nature21075 [8] HAN S C, LEE J W, KANG K. A new type of low density material: shellular[J]. Advanced Materials, 2015, 27(37): 5506-5511. doi: 10.1002/adma.201501546 [9] KASHANI H, ITO Y, HAN J, et al. Extraordinary tensile strength and ductility of scalable nanoporous graphene[J]. Science Advances, 2019, 5(2): eaat6951. doi: 10.1126/sciadv.aat6951 [10] QI J, CHEN Z, JIANG P, et al. Recent progress in active mechanical metamaterials and construction principles[J]. Advanced Materials, 2022, 9(1): 2102662. [11] YANG C, BOORUGU M, DOPP A, et al. 4D printing reconfigurable, deployable and mechanically tunable metamaterials[J]. Materials Horizons, 2019, 6: 1244-1250. doi: 10.1039/C9MH00302A [12] WAGNER M A, LUMPE T S, CHEN T, et al. Programmable, active lattice structures: unifying stretch-dominated and bending-dominated topologies[J]. Extreme Mechanics Letters, 2019, 29: 100461. doi: 10.1016/j.eml.2019.100461 [13] LEI M, HONG W, ZHAO Z, et al. 3D printing of auxetic metamaterials with digitally reprogrammable shape[J]. ACS Applied Materials and Interfaces, 2019, 11(25): 22768-22776. doi: 10.1021/acsami.9b06081 [14] NIMMAGADDA C, MATLACK K H. Thermally tunable band gaps in architected metamaterial structures[J]. Journal of Sound and Vibration, 2019, 439: 29-42. doi: 10.1016/j.jsv.2018.09.053 [15] DENG F, NGUYEN Q, ZHANG P. Multifunctional liquid metal lattice materials through hybrid design and manufacturing[J]. Additive Manufacturing, 2020, 33: 101117. doi: 10.1016/j.addma.2020.101117 [16] KOTIKIAN A, MCMAHAN C, DAVIDSON E C, et al. Untethered soft robotic matter with passive control of shape morphing and propulsion[J]. Science Robotics, 2019, 4(33): eaax7044. doi: 10.1126/scirobotics.aax7044 [17] WHITE T J, BROER D J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers[J]. Nature Materials, 2015, 14: 1087-1098. doi: 10.1038/nmat4433 [18] JACKSON J A, MESSNER M C, DUDUKOVIC N A, et al. Field responsive mechanical metamaterials[J]. Science Advances, 2018, 4(12): eaau6419. doi: 10.1126/sciadv.aau6419 [19] KIM Y, YUK H, ZHAO R, et al. Printing ferromagnetic domains for untethered fast-transforming soft materials[J]. Nature, 2018, 558: 274-279. doi: 10.1038/s41586-018-0185-0 [20] XU T, ZHANG J, SALEHIZADEH M, et al. Millimeter-scale flexible robots with programmable three-dimensional magnetization and motions[J]. Science Robotics, 2019, 4(29): eaav4494. doi: 10.1126/scirobotics.aav4494 [21] CUI J, HUANG T, LUO Z, et al. Nanomagnetic encoding of shape-morphing micromachines[J]. Nature, 2019, 575: 164-168. doi: 10.1038/s41586-019-1713-2 [22] ZE Q, KUANG X, WU S, et al. Magnetic shape memory polymers with integrated multifunctional shape manipulation[J]. Advanced Materials, 2020, 32(4): e1906657. doi: 10.1002/adma.201906657 [23] LI C, LAU G C, YUAN H, et al. Fast and programmable locomotion of hydrogel-metal hybrids under light and magnetic fields[J]. Science Robotics, 2020, 5(49): eabb9822. doi: 10.1126/scirobotics.abb9822 [24] WANG S, GAO Y, WEI A, et al. Asymmetric elastoplasticity of stacked graphene assembly actualizes programmable untethered soft robotics[J]. Nature Communications, 2020, 11: 4359. doi: 10.1038/s41467-020-18214-0 [25] CUI H, HENSLEIGH R, YAO D, et al. Three-dimensional printing of piezoelectric materials with designed anisotropy and directional response[J]. Nature Materials, 2019, 18(3): 234-241. doi: 10.1038/s41563-018-0268-1 [26] ZHANG Q, KUANG X, WENG S, et al. Shape-memory balloon structures by pneumatic multi-material 4D printing[J]. Advanced Functional Materials, 2021, 31(21): 2010872. doi: 10.1002/adfm.202010872 [27] HAWKES E W, BLUMENSCHEIN L H, GREER J D, et al. A soft robot that navigates its environment through growth[J]. Science Robotics, 2017, 2(8): eaan3028. doi: 10.1126/scirobotics.aan3028 [28] RAFSANJANI A, ZHANG Y, LIU B, et al. Kirigami skins make a simple soft actuator crawl[J]. Science Robotics, 2018, 3(15): eaar7555. doi: 10.1126/scirobotics.aar7555 [29] XIA X, AFSHAR A, PORTELA C M, et al. Electrochemically reconfigurable architected materials[J]. Nature, 2019, 573: 205-213. doi: 10.1038/s41586-019-1538-z [30] DEHGHANY M, ZHANG H, NAGHDABADI R, et al. A thermodynamically-consistent large deformation theory coupling photochemical reaction and electrochemistry for light-responsive gels[J]. Journal of the Mechanics and Physics of Solids, 2018, 116: 239-266. doi: 10.1016/j.jmps.2018.03.018 [31] LI S, DENG B, GRINTHAL A, et al. Liquid-induced topological transformations of cellular microstructures[J]. Science Robotics, 2021, 592: 386-391. [32] LIU J, GU T, SHAN S, et al. Harnessing buckling to design architected materials that exhibit effective negative swelling[J]. Advanced Materials, 2016, 28(31): 6619-6624. doi: 10.1002/adma.201600812 [33] ZHANG H, GUO X, WU J, et al. Soft mechanical metamaterials with unusual swelling behavior and tunable stress-strain curves[J]. Science Advances, 2018, 4(6): eaar8535. doi: 10.1126/sciadv.aar8535 [34] TUMBLESTON J R, SHIRVANYANTS D, ERMOSHKIN N, et al. Continuous liquid interface production of 3D objects[J]. Science, 2015, 347(6228): 1349-1352. doi: 10.1126/science.aaa2397 [35] ROBERTSON I D, YOURDKHANI M, CENTELLAS P J, et al. Rapid energy-efficient manufacturing of polymers and composites via frontal polymerization[J]. Nature, 2018, 557: 223-227. doi: 10.1038/s41586-018-0054-x [36] BOLEY J W, REES W M, LISSANDRELLO C, et al. Shape-shifting structured lattices via multimaterial 4D printing[J]. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(42): 20856-20862. doi: 10.1073/pnas.1908806116 [37] SKYLAR-SCOTT M A, MUELLER J, VISSER C W, et al. Voxelated soft matter via multimaterial multinozzle 3D printing[J]. Nature, 2019, 575(7782): 330-335. doi: 10.1038/s41586-019-1736-8 [38] KELLY B E, BHATTACHARYA I, HEIDARI H, et al. Volumetric additive manufacturing via tomographic reconstruction[J]. Nature, 2019, 363(6431): 1075-1079. [39] WEI K, CHEN H, PEI Y, et al. Planar lattices with tailorable coefficient of thermal expansion and high stiffness based on dual-material triangle unit[J]. Journal of the Mechanics and Physics of Solids, 2016, 86: 173-191. doi: 10.1016/j.jmps.2015.10.004 [40] XU H, FARAG A, PASINI D. Multilevel hierarchy in bi-material lattices with high specific stiffness and unbounded thermal expansion[J]. Acta Materialia, 2017, 134: 155-166. doi: 10.1016/j.actamat.2017.05.059 [41] TANIKER S, CELLI P, PASINI D, et al. Temperature-induced shape morphing of bi-metallic structures[J]. International Journal of Solids and Structures, 2020, 190: 22-32. doi: 10.1016/j.ijsolstr.2019.10.024 [42] GUO X, NI X, LI J, et al. Designing mechanical metamaterials with kirigami-inspired, hierarchical constructions for giant positive and negative thermal expansion[J]. Advanced Materials, 2020, 33(3): 2004919. [43] LIU L, QIAO C, AN H, et al. Encoding kirigami bi-materials to morph on target in response to temperature[J]. Scientific Reports, 2019, 9: 19499. doi: 10.1038/s41598-019-56118-2 [44] BOATTI E, VASIOS N, BERTOLDI K. Origami metamaterials for tunable thermal expansion[J]. Advanced Materials, 2017, 29(26): 1700360. doi: 10.1002/adma.201700360 [45] NI X, GUO X, LI J, et al. 2D mechanical metamaterials with widely tunable unusual modes of thermal expansion[J]. Advanced Materials, 2019, 31(48): 1905405. doi: 10.1002/adma.201905405 [46] JANBAZ S, NAROOEI K, VAN MANEN T, et al. Strain rate-dependent mechanical metamaterials[J]. Science Advances, 2020, 6(25): eaba0616. doi: 10.1126/sciadv.aba0616 [47] CHE K, YUAN C, QI H J, et al. Viscoelastic multistable architected materials with temperature-dependent snapping sequence[J]. Soft Matter, 2018, 14(13): 2492-2499. doi: 10.1039/C8SM00217G [48] YUAN C, MU X, DUNN C K, et al. Thermomechanically triggered two-stage pattern switching of 2D lattices for adaptive structures[J]. Advanced Functional Materials, 2018, 28(18): 1705727. doi: 10.1002/adfm.201705727 [49] SONG C, JU J. Reconfigurable mesostructures with prestressing, reverse stiffness and shape memory effects[J]. Extreme Mechanics Letters, 2020, 35: 100625. doi: 10.1016/j.eml.2019.100625 [50] SONG C, ZOU B, CUI Z, et al. Thermomechanically triggered reversible multi-transformability of a single material system by energy swapping and shape memory effects[J]. Advanced Functional Materials, 2021, 31(32): 2101395. doi: 10.1002/adfm.202101395 [51] JEONG H Y, LEE E, HA S, et al. Multistable thermal actuators via multimaterial 4D printing[J]. Advanced Materials Technologies, 2018, 4(3): 1800495. [52] ZHAO Z, YUAN C, LEI M, et al. Three-dimensionally printed mechanical metamaterials with thermally tunable auxetic behavior[J]. Physical Review Applied, 2019, 11: 044074. doi: 10.1103/PhysRevApplied.11.044074 [53] MUELLER J, LEWIS J A, BERTOLDI K. Architected multimaterial lattices with thermally programmable mechanical response[J]. Advanced Functional Materials, 2022, 32(1): 2105128. doi: 10.1002/adfm.202105128 [54] 王信涛. 三维有序负泊松比结构的设计、制备与力学性能表征[D]. 博士学位论文. 哈尔滨: 哈尔滨工业大学, 2018.WANG Xintao. The design, fabrication and mechanical characterization of three-dimensional periodic auxetic cellular structures[D]. PhD Thesis. Harbin: Harbin Institute of Technology, 2018. (in Chinese) [55] YANG H, WANG B, MA L. Designing hierarchical metamaterials by topology analysis with tailored Poisson’s ratio and Young’s modulus[J]. Composite Structures, 2019, 214: 359-378. doi: 10.1016/j.compstruct.2019.01.076 [56] YANG H, MA L. Design and characterization of axisymmetric auxetic metamaterials[J]. Composite Structures, 2020, 249: 112560. doi: 10.1016/j.compstruct.2020.112560 [57] YANG H, WANG B, MA L. Mechanical properties of 3D double-U auxetic structures[J]. International Journal of Solids and Structures, 2019, 180/181: 13-29. doi: 10.1016/j.ijsolstr.2019.07.007 [58] YANG H, MA L. Impact resistance of additively manufactured 3D double-U auxetic structures[J]. Thin-Walled Structures, 2021, 169: 108373. doi: 10.1016/j.tws.2021.108373 [59] YANG H, MA L. Multi-material 3D double-V metastructures with tailorable Poisson’s ratio and thermal expansion[J]. International Journal of Mechanical Sciences, 2021, 210: 106733. doi: 10.1016/j.ijmecsci.2021.106733 [60] 李明. 可调泊松比和热膨胀系数的双V结构设计和性能表征[D]. 硕士学位论文. 哈尔滨: 哈尔滨工业大学, 2021LI Ming. Composite double-V honeycombs with tailorable Poisson’s ratio and thermal expansion[D]. Master Thesis. Harbin: Harbin Institute of Technology, 2021. (in Chinese) [61] HAGHPANAH B, SALARI-SHARIF L, POURRAJAB P, et al. Multistable shape-reconfigurable architected materials[J]. Advanced Materials, 2016, 28(36): 7915-7920. doi: 10.1002/adma.201601650 [62] FRENZEL T, FINDEISEN C, KADIC M, et al. Tailored buckling microlattices as reusable light-weight shock absorbers[J]. Advanced Materials, 2016, 28(28): 5865-5870. doi: 10.1002/adma.201600610 [63] YANG H, MA L. Multi-stable mechanical metamaterials with shape-reconfiguration and zero Poisson’s ratio[J]. Materials and Design, 2018, 152: 181-190. doi: 10.1016/j.matdes.2018.04.064 [64] YANG H, MA L. Multi-stable mechanical metamaterials by elastic buckling instability[J]. Journal of Materials Science, 2019, 54: 3509-3526. doi: 10.1007/s10853-018-3065-y [65] YANG H, MA L. 1D and 2D snapping mechanical metamaterials with cylindrical topology[J]. International Journal of Solids and Structures, 2020, 204/205: 220-232. doi: 10.1016/j.ijsolstr.2020.08.023 [66] YANG H, MA L. 1D to 3D multi-stable architected materials with zero Poisson’s ratio and controllable thermal expansion[J]. Materials and Design, 2020, 188: 108430. doi: 10.1016/j.matdes.2019.108430 [67] YANG H, MA L. Angle-dependent transitions between structural bistability and multistability[J]. Advanced Engineering Materials, 2020, 22(5): 1900871. doi: 10.1002/adem.201900871 [68] 周益民. 基于双稳态机制的可调控热膨胀结构设计及其性能表征[D]. 硕士学位论文. 哈尔滨: 哈尔滨工业大学, 2021.ZHOU Yimin. Design and performance characterization of adjustable thermal expansion structure based on bistable mechanism[D]. Master Thesis. Harbin: Harbin Institute of Technology, 2021. (in Chinese) [69] FINDEISEN C, HOHE J, KADIC M, et al. Characteristics of mechanical metamaterials based on buckling elements[J]. Journal of the Mechanics and Physics of Solids, 2017, 102: 151-164. doi: 10.1016/j.jmps.2017.02.011 [70] RAFSANJANI A, AKBARAZADEH A, PASINI D. Snapping mechanical metamaterials under tension[J]. Advanced Materials, 2015, 27(39): 5931-5935. doi: 10.1002/adma.201502809 [71] LI C W, TANG X, MUÑOZ J A, et al. Structural relationship between negative thermal expansion and quartic anharmonicity of cubic ScF3[J]. Physical Review Letters, 2011, 107: 195504. doi: 10.1103/PhysRevLett.107.195504 [72] TAKENAKA K, SHINODA T, INOUE N, et al. Giant negative thermal expansion in Fe-doped layered ruthenate ceramics[J]. Applied Physics Express, 2017, 10: 115501. doi: 10.7567/APEX.10.115501 [73] EVANS J S O, MARY T A, Sleight A W. Negative thermal expansion in Sc2(WO4)3[J]. Journal of Solid State Chemistry, 1998, 137(1): 148-160. doi: 10.1006/jssc.1998.7744 [74] EVANS J S O, MARY T A, VOGT T, et al. Negative thermal expansion in ZrW2O8 and HfW2O8[J]. Chemistry of Materials, 1996, 8(12): 2809-2823. doi: 10.1021/cm9602959 [75] TAKENAKA K, TAKAGI H. Giant negative thermal expansion in Ge-doped anti-perovskite manganese nitrides[J]. Applied Physics Letters, 2005, 87(26): 261902. doi: 10.1063/1.2147726 [76] KWON Y K, BERBER S, TOMÁNEK D. Thermal contraction of carbon fullerenes and nanotubes[J]. Physical Review Letters, 2004, 92(1): 015901. doi: 10.1103/PhysRevLett.92.015901 [77] JIANG H, LIU B, HUANG Y, et al. Thermal expansion of single wall carbon nanotubes[J]. Journal of Engineering Materials and Technology, 2004, 126(3): 265-270. doi: 10.1115/1.1752925 [78] GOODWIN A L, KEPERT C J. Negative thermal expansion and low-frequency modes in cyanide-bridged framework materials[J]. Physical Review B, 2005, 71: 140301. doi: 10.1103/PhysRevB.71.140301 [79] WEI K, PENG Y, WEN W, et al. Tailorable thermal expansion of lightweight and robust dual-constituent triangular lattice material[J]. Journal of Applied Mechanics, 2017, 84(10): 101006. [80] AI L, GAO X L. Three-dimensional metamaterials with a negative Poisson’s ratio and a non-positive coefficient of thermal expansion[J]. International Journal of Mechanical Sciences, 2018, 135: 101-113. doi: 10.1016/j.ijmecsci.2017.10.042 [81] GDOUTOS E, SHAPIRO A A, DARAIO C. Thin and thermally stable periodic metastructures[J]. Experimental Mechanics, 2013, 53: 1735-1742. doi: 10.1007/s11340-013-9748-z [82] LI Y, CHEN Y, LI T, et al. Hoberman-sphere-inspired lattice metamaterials with tunable negative thermal expansion[J]. Composite Structures, 2018, 189: 586-597. doi: 10.1016/j.compstruct.2018.01.108 [83] XIE Y, PEI X, YU J. Double-layer sandwich annulus with ultra-low thermal expansion[J]. Composite Structures, 2018, 203: 709-717. doi: 10.1016/j.compstruct.2018.07.075 [84] YAMAMOTO N, GDOUTOS E, TODA R, et al. Thin films with ultra-low thermal expansion[J]. Advanced Materials, 2014, 26(19): 3076-3080. doi: 10.1002/adma.201304997 [85] LI X, GAO L, ZHOU W, et al. Novel 2D metamaterials with negative Poisson’s ratio and negative thermal expansion[J]. Extreme Mechanics Letters, 2019, 30: 100498. doi: 10.1016/j.eml.2019.100498 [86] HA C S, HESTEKIN E, LI J H, et al. Controllable thermal expansion of large magnitude in chiral negative Poisson’s ratio lattices[J]. Physica Status B: Basic Solid State Physics, 2015, 252(7): 1431-1434. doi: 10.1002/pssb.201552158 [87] WU L, LI B, ZHOU J. Isotropic negative thermal expansion metamaterials[J]. ACS Applied Materials and Interfaces, 2016, 8(27): 17721-17727. doi: 10.1021/acsami.6b05717 [88] TAKEZAWA A, KOBASHI M. Design methodology for porous composites with tunable thermal expansion produced by multi-material topology optimization and additive manufacturing[J]. Composites Part B, 2017, 131: 21-29. doi: 10.1016/j.compositesb.2017.07.054 [89] TAKEZAWA A, KOBASHI M, KITAMURA M. Porous composite with negative thermal expansion obtained by photopolymer additive manufacturing[J]. APL Materials, 2015, 3(7): 076103. doi: 10.1063/1.4926759 [90] LENDLEIN A, KELCH S. Shape-memory polymers[J]. Angewandte Chemie International Edition, 2002, 41: 2034-2057. doi: 10.1002/1521-3773(20020617)41:12<2034::AID-ANIE2034>3.0.CO;2-M [91] LIU C, QIN H, MATHER P T. Review of progress in shape-memory polymers[J]. Journal of Materials Chemistry, 2007, 16: 1543-1558. [92] ZHAO Q, QI H J, XIE T. Recent progress in shape memory polymer: new behavior, enabling materials, and mechanistic understanding[J]. Progress in Polymer Science, 2015, 49/50: 79-120. doi: 10.1016/j.progpolymsci.2015.04.001 [93] DING Z, YUAN C, PENG X, et al. Direct 4D printing via active composite materials[J]. Science Advances, 2017, 3(4): e1602890. doi: 10.1126/sciadv.1602890 [94] DELAEY J, DUBRUEL P, VLIERBERGHE S V. Shape-memory polymers for biomedical applications[J]. Advanced Functional Materials, 2020, 30(44): 1909047. doi: 10.1002/adfm.201909047 -




 下载:
下载:
































































 渝公网安备50010802005915号
渝公网安备50010802005915号