Thermal Shock Crack Propagation of Alumina Simulated With the Phase-Field Method Under Temperature-Dependent Damage Criteria
-
摘要:
氧化铝陶瓷材料的力学性能受温度影响显著，因此使用相场法模拟热冲击裂纹的扩展时有必要考虑损伤判据的温度相关性。在现有热力学相场模型的基础上通过引入温度相关性损伤判据，修正了相场模型的控制方程。利用该模型对氧化铝陶瓷热冲击实验进行有限元模拟，并将模拟结果与氧化铝热冲击实验结果和不考虑温度相关性损伤判据的有限元模拟结果进行对比。结果表明，通过引入温度相关性损伤判据，可实现对热冲击裂纹的萌生和扩展过程更合理的模拟。
Abstract:The mechanical properties of alumina ceramic materials are significantly affected by temperature, so it is necessary to consider the temperature dependence of the damage criteria during the simulation of thermal shock crack propagation with the phase-field method. Based on the existing thermodynamic phase-field model, the governing equations for the phase-field model were modified through introduction of the temperature-dependent damage criterion. Then the revised phase-field model was used to simulate the thermal shock experiment of alumina ceramics, and the simulation results were compared with the experimental results and the finite element simulation results without temperature-dependent damage criteria. The results show that, introduction of the temperature-dependent damage criterion helps more reasonably simulate the initiation and propagation process of thermal shock crack.
-
Key words:
- alumina ceramic /
- thermal shock /
- phase-field method /
- finite element simulation
-
图 1 x=0处尖锐和弥散裂纹拓扑：(a)尖锐裂纹；(b) 弥散裂纹，用长度尺度l表示裂纹相场
$ \bar{d} $ Figure 1. Topologies of sharp and diffuse cracks at x=0: (a) the sharp crack; (b) phase field
$ \bar{d} $ of the diffuse crack denoted by length scale l
图 4 裂纹相场和温度场随时间的演化
Figure 4. Evolution of the crack phase field and the temperature field with time
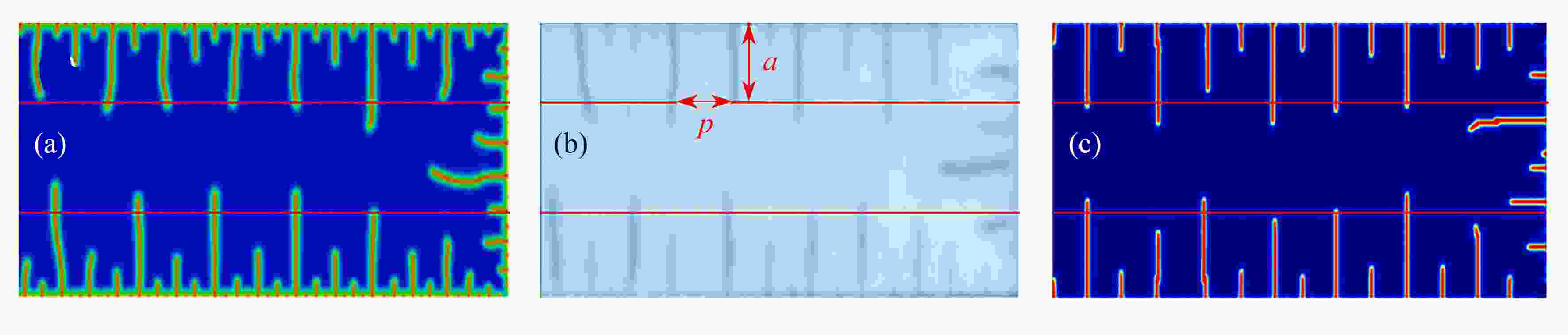
图 5 水淬实验结果与有无考虑温度相关性损伤判据模拟结果的对比：(a) Chu等[13]的模拟结果；(b)实验结果[6]；(c) 本文模拟结果
Figure 5. Comparison between water quenching experimental results and simulation results with or without temperature-dependent damage criteria: (a) simulation results of Chu et al [13]; (b) the experimental results [6]; (c) simulation results of this paper
图 6 圆盘热冲击问题的几何模型和热边界条件（红色区域表示外加热流）
Figure 6. The geometric model and thermal boundary conditions for thermal shock problems of disks (the red area represents applied heat flow)
图 7 圆盘辐射加热实验结果和模拟结果
Figure 7. Experimental results of radiation heating and simulation results of the phase field method
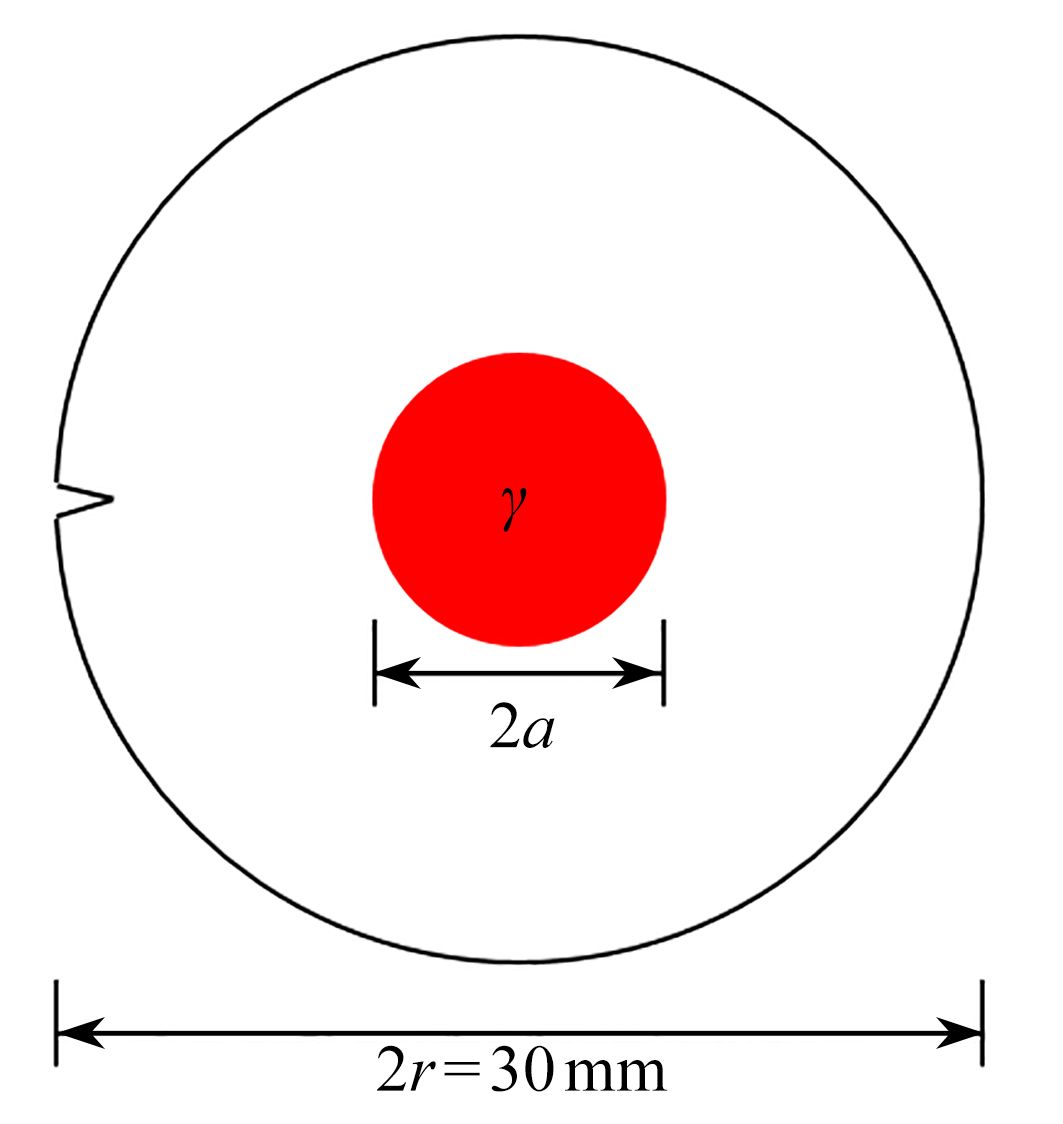
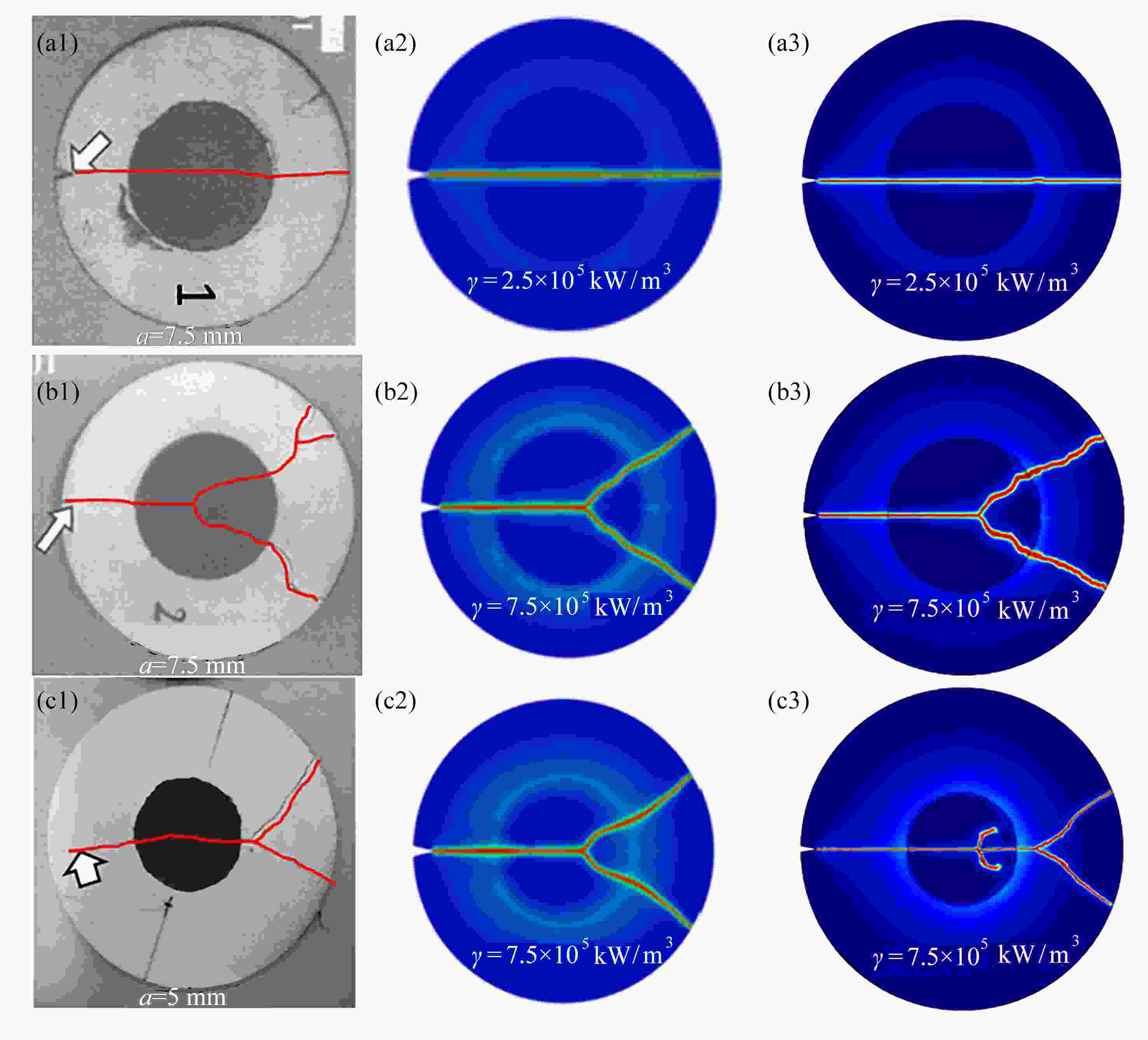
图 8 圆盘辐射加热实验结果和模拟结果： (a)实验结果；(b) 考虑温度相关性临界能量释放率Gc(T)的模拟结果；(c) 不考虑温度相关性临界能量释放率Gc的模拟结果
Figure 8. Experimental and simulation results of disk radiation heating: (a) the experimental results; (b) the simulation results with temperature-dependent critical energy release rate Gc(T); (c) the simulation results without temperature-dependent critical energy release rate Gc
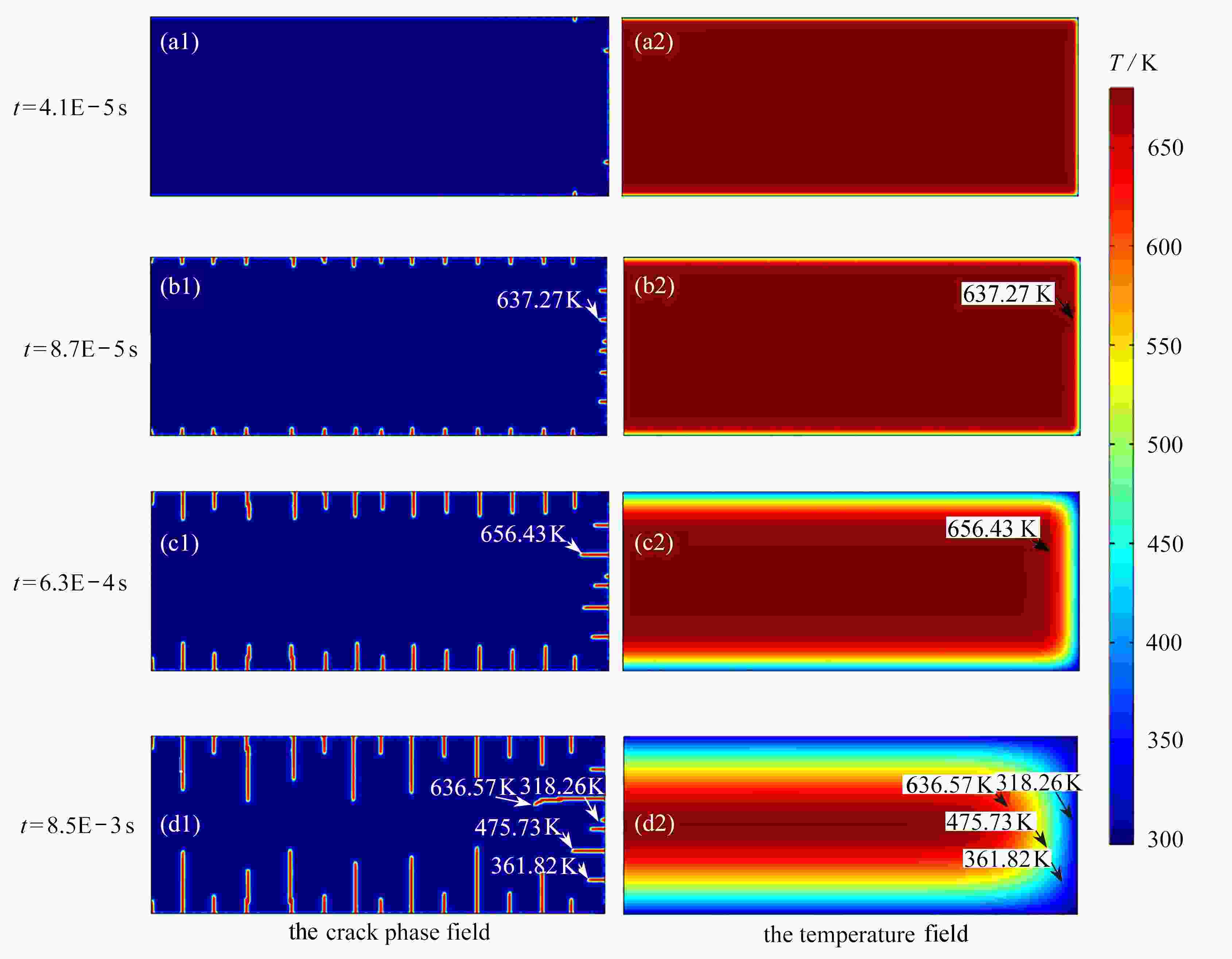
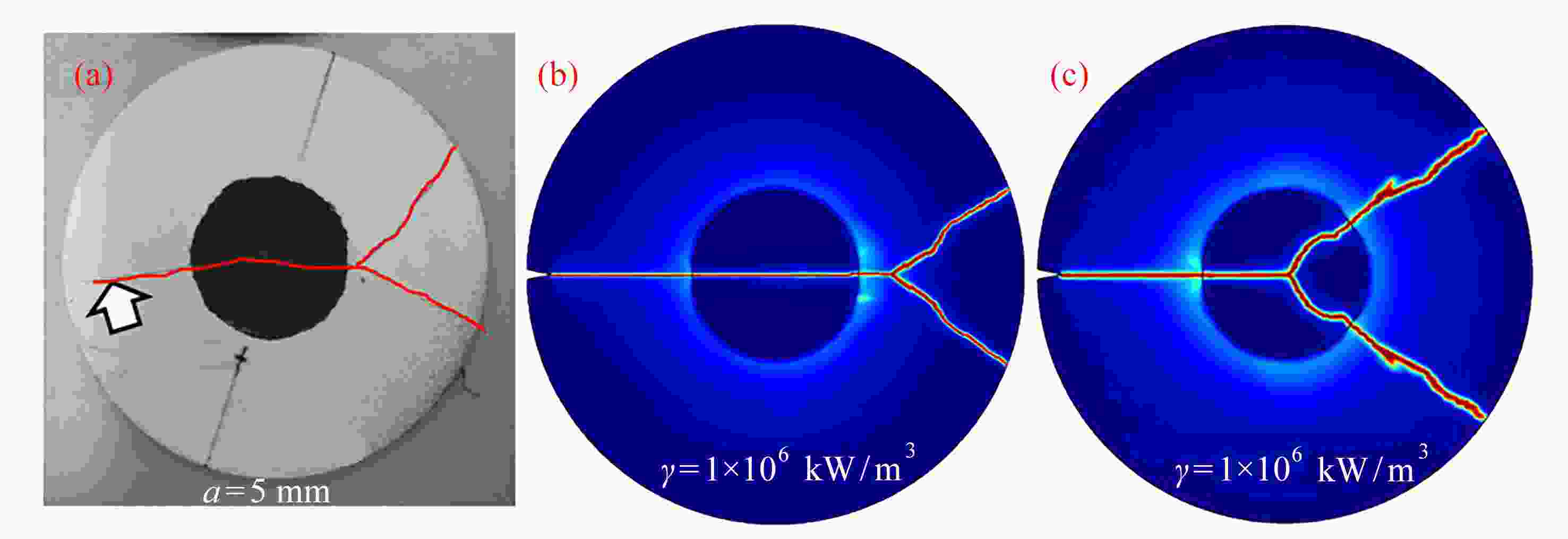
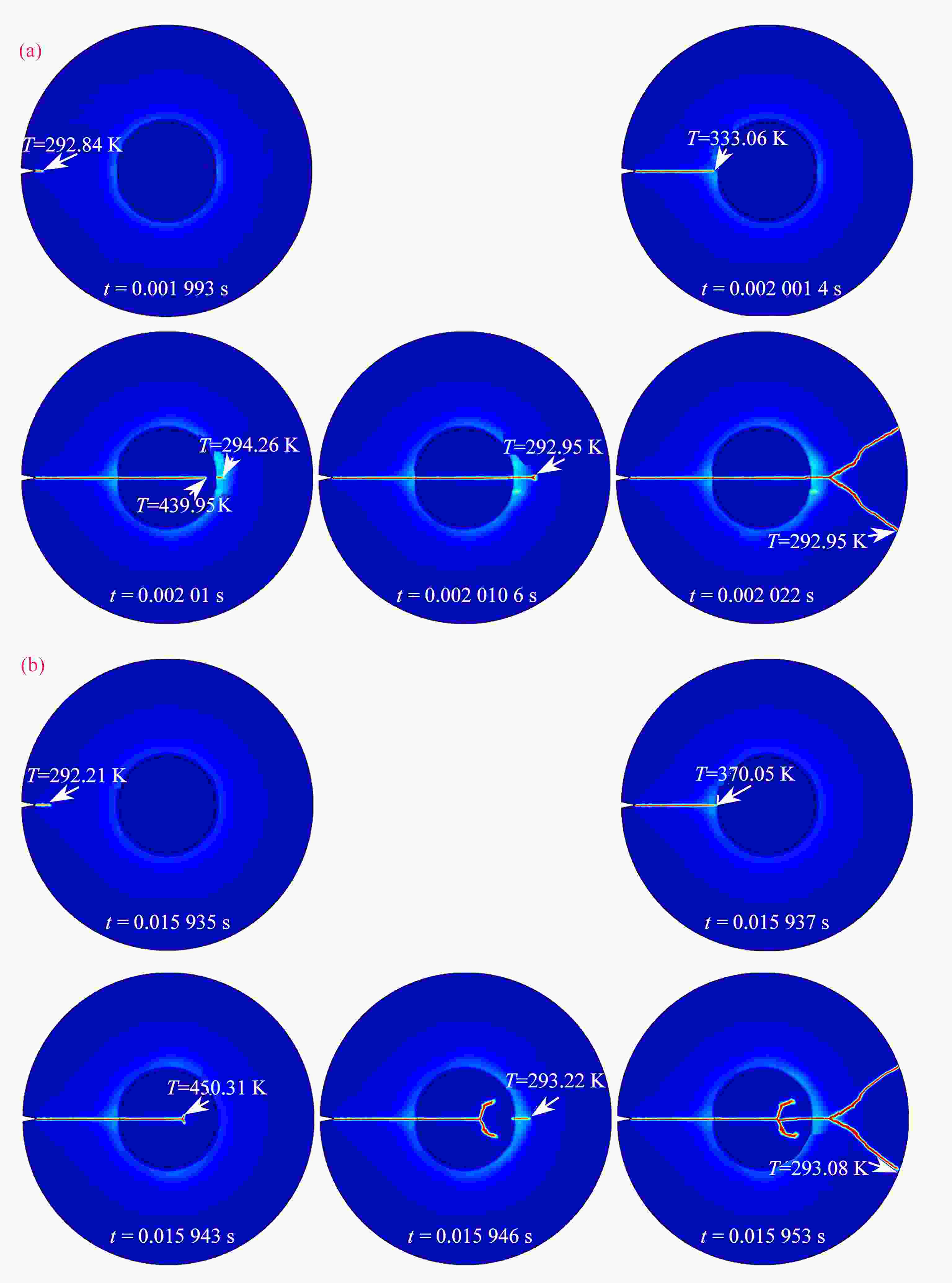
图 9 不同热流密度下的裂纹和裂纹尖端温度随时间的演化：(a)
$ \gamma =7.5\times {10}^{5}\;\mathrm{k}\mathrm{W}/{\mathrm{m}}^{3} $ ；(b)$\gamma =1\times {10}^{6}\;\mathrm{k}\mathrm{W}/{\mathrm{m}}^{3}$ Figure 9. Evolution of crack and crack tip temperatures with time under different heat fluxes: (a)
$ \gamma =7.5\times {10}^{5}\;\mathrm{k}\mathrm{W}/{\mathrm{m}}^{3} $ ; (b)$\gamma =1\times {10}^{6}\;\mathrm{k}\mathrm{W}/{\mathrm{m}}^{3}$ material parameter value or expression elastic modulus $ E/{\text{GPa}} $ $340 - 2.54T{\exp({ - {T_{\rm{m} } } }/T}) + 1.9( {T - 0.363{T_{\rm{m} } } + | {T - 0.363{T_{\rm{m} } } } |} ){\exp ({ { { - {T_{\rm{m} } } } / T} } )}$ density $ \rho /( {{{\text{g}} / {{\text{c}}{{\text{m}}^{\text{3}}}}}} ) $ 6.119 Poisson’s ratio $ \upsilon $ 0.22 melting point $ {T_{\rm{m}}}/{\text{K}} $ 2327.15 thermal conductivity $ k/( {{{\text{W}} / {( {{\text{m}} \cdot {\text{K}}} )}}} ) $ $ 210.75\ln ( T ) - 746.28 $ heat capacity $ C_p/( {{{\text{J}} / {( {{\text{kg}} \cdot {\text{K}}} )}}} ) $ $60.225 - 0.011\;28T + 1.244\;56 \times {10^{ - 6} }\times{T^2}$ thermal expansion $ \alpha /( {{{\text{1}} / {\text{K}}}} ) $ $( {6.52 + 6.811\;4 \times { {10}^{ - 4} }\times T} ){\text{ } } \times {10^{ - 6} }$ 
下载: 导出CSV
material parameter value or expression elastic modulus $ E{\text{/GPa}} $ $380 - 2.54T{\exp ({ { { - {T_{\rm{m} } } } / T} } }) + 1.9( {T - 0.363{T_{\rm{m} } } + | {T - 0.363{T_{\rm{m} } } } |} ){\exp( { { { - {T_{\rm{m} } } } / T} } )}$ density $ \rho /( {{{\text{g}} / {{\text{c}}{{\text{m}}^{\text{3}}}}}} ) $ 3.90 Poisson’s ratio $ \upsilon $ 0.25 melting point $ {T_{\rm{m}}}/{\text{K}} $ 2327.15 thermal conductivity $k/( { { {\text{W} } / ({ {\text{m} } \cdot {\text{K} } } }} ) )$ $31.06 - 0.113\;8 T + 2.95 \times {10^{ - 4} } \times {T^2} - 4.43 \times {10^{ - 7} } \times {T^3}$ heat capacity $ C_p/( {{{\text{J}} / {( {{\text{kg}} \cdot {\text{K}}} )}}} ) $ $60.225 - 0.011\;28T + 1.244\;56 \times {10^{ - 6} }\times {T^2}$ thermal expansion $ \alpha /( {{1 / {\text{K}}}} ) $ $60.225 - 0.011\;28T + 1.244\;56 \times {10^{ - 6} }\times {T^2}$
下载: 导出CSV
-
[1] KINGERY W D. Factors affecting thermal stress resistance of ceramic materials[J]. Journal of the American Ceramic Society, 2010, 38(1): 3-15. [2] MENOUILLARD T, BELYTSCHKO T. Analysis and computations of oscillating crack propagation in a heated strip[J]. International Journal of Fracture, 2011, 167: 57-70. doi: 10.1007/s10704-010-9519-0 [3] 吴大方, 王怀涛, 朱芳卉. 1 200 ℃高温环境下部件受热前表面应变的光学测量[J]. 应用数学和力学, 2018, 39(6): 631-644WU Dafang, WANG Huaitao, ZHU Fanghui. Optical measurement of heated-front-surface strains for components in high temperature environments up to 1 200 ℃[J]. Applied Mathematics and Mechanics, 2018, 39(6): 631-644.(in Chinese) [4] LI D, WANG R, WANG X, et al. Simulation of the thermal shock cracking behaviors of ceramics under water quenching for 3-dimension conditions[J]. European Journal of Mechanics A: Solids, 2020, 84: 104080. doi: 10.1016/j.euromechsol.2020.104080 [5] WU J Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure[J]. Journal of the Mechanics and Physics of Solids, 2017, 103: 72-99. doi: 10.1016/j.jmps.2017.03.015 [6] SHAO Y, ZHANG Y, XU X. Effect of crack pattern on the residual strength of ceramics after quenching[J]. Journal of the American Ceramic Society, 2011, 94: 72-99. [7] HONDA S, OGIHARA Y, KISHI T, et al. Estimation of thermal shock resistance of fine porous alumina by infrared radiation heating method[J]. Nippon Seramikkusu Kyokai Gakujutsu Ronbunshi, 2009, 117(1371): 1208-1215. doi: 10.2109/jcersj2.117.1208 [8] HONDA S, SUZUKI T, NISHIKAWA T, et al. Estimation of thermal shock properties for silicon nitride having high thermal conductivity[J]. Journal of the Ceramic Society of Japan, 2010, 110(1277): 38-43. [9] KARMA A, KESSLER D A, LEVINE H. Phase-field model of mode Ⅲ dynamic fracture[J]. Physical Review Letters, 2001, 87: 045501. doi: 10.1103/PhysRevLett.87.045501 [10] 李家宇, 曾忠, 乔龙. 相场方法模拟液滴的动态润湿行为[J]. 应用数学和力学, 2019, 40(9): 957-967LI Jiayu, ZENG Zhong, QIAO Long. Numerical simulation of droplets’ dynamic wetting process with the phase field method[J]. Applied Mathematics and Mechanics, 2019, 40(9): 957-967.(in Chinese) [11] MICHE C, SCHÄNZEL LM, ULMER H. Phase field modeling of fracture in multi-physics problems, part Ⅰ: balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 294: 449-485. doi: 10.1016/j.cma.2014.11.016 [12] 柳占立, 初东阳, 王涛, 等. 爆炸和冲击载荷下金属材料及结构的动态失效仿真[J]. 应用数学和力学, 2021, 42(1): 1-14 doi: 10.1007/s10483-021-2692-5LIU Zhanli, CHU Dongyang, WANG Tao, et al. Dynamic failure simulation of metal materials and structures under blast and impact loading[J]. Applied Mathematics and Mechanics, 2021, 42(1): 1-14.(in Chinese) doi: 10.1007/s10483-021-2692-5 [13] CHU D, LI X, LIU Z. Study the dynamic crack path in brittle material under thermal shock loading by phase field modeling[J]. International Journal of Fracture, 2017, 208: 115-130. doi: 10.1007/s10704-017-0220-4 [14] LI D, LI W, WANG R, et al. Simulation of the thermal shock behavior of ultra-high temperature ceramics with the consideration of temperature-dependent crack propagation criterion and interaction between thermal shock cracks evolution and thermal conduction[J]. European Journal of Mechanics A: Solids, 2018, 72: 268-274. doi: 10.1016/j.euromechsol.2018.05.016 [15] MIEHE C, HOFACKER M, WELSCHINGER F. A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(45/48): 2765-2778. [16] 李定玉. 计及使役环境的高温陶瓷材料抗热震性能及表征方法研究[D]. 博士学位论文. 重庆: 重庆大学, 2015.LI Dingyu. Research of thermal shock resistance of high temperature ceramics and its characterization methods with the consideration of different operating environments[D]. PhD Thesis. Chongqing: Chongqing University, 2015. (in Chinese) -
计量
- 文章访问数: 642
- HTML全文浏览量: 351
- PDF下载量: 97
- 被引次数: 0
渝公网安备50010802005915号