基于人工神经网络的共振吸声超材料声学性能快速预测及结构优化设计
doi: 10.21656/1000-0887.450170
Acoustic Performance Rapid Prediction and Structural Optimization for Resonant Sound-Absorbing Metamaterials Based on Artificial Neural Networks
-
摘要: 针对共振吸声超材料声学性能快速预测及结构优化设计需求,提出了一种基于人工神经网络的共振吸声超材料性能预测方法. 首先, 建立了由微穿孔板和Helmholtz共振腔组成的多层穿孔型共振吸声超材料的理论模型,并通过仿真与实验验证其正确性;随后,通过理论模型生成数据集,并以此为基础,采用BP(back propagation)神经网络原理,搭建了结构特征参量与声学性能的人工神经网络模型;之后,将训练后的人工神经网络模型与遗传算法相结合,对共振吸声超材料进行声学性能最优化设计. 结果表明:训练后的人工神经网络模型可以对目标结构的吸声性能进行准确预测,并且预测效率相较理论模型提高50%以上;人工神经网络模型与优化算法的结合不仅能提高优化效率,优化后的结构也具有良好的低频宽带吸声性能. 人工神经网络为大规模结构性能预测计算提供了便利,在超材料等结构设计及优化领域具有广阔的应用前景.Abstract: A sound performance prediction method based on the artificial neural network (ANN) was proposed to meet the requirements of rapid prediction and optimization design of resonant sound-absorbing metamaterials. Firstly, a theoretical model was established for multilayer perforated resonant sound-absorbing metamaterials (MPRSMs) composed of microperforated panels and Helmholtz resonators, which was then verified through simulation and experiments; subsequently, a dataset was generated with the theoretical model, and in turn an ANN model was constructed by means of the back propagation (BP) neural network to build the mapping relationship between structural parameters and acoustic performances; afterwards, the trained ANN model was combined with the genetic algorithm to optimize the acoustic performance of the MPRSMs. The results show that, the trained ANN model can accurately predict the sound absorption performance of the MPRSMs, and the prediction efficiency improves by more than 50% compared to the theoretical model; the combination of the ANN model and the optimization algorithm can not only improve the optimization efficiency, but bring good low-frequency broadband sound absorption performance of the optimized structure. The ANN provides convenience for large-scale structural performance prediction calculations and has broad application prospects in structural design and optimization of metamaterials.
-
Key words:
- resonant sound-absorbing metamaterial /
- artificial neural network /
- sound absorption coefficient /
- BP neural network /
- genetic algorithm
edited-byedited-by1) (我刊青年编委孟晗来稿) -
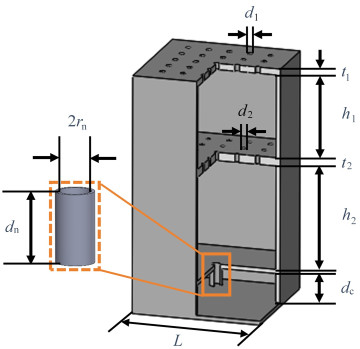
表 1 MPRSM结构模型几何参数
Table 1. Geometric parameters of the MPRSM structural model
geometric parameter value the 1st perforated plate thickness t1/mm 1.1 the 1st perforated plate hole diameter d1/mm 1.2 the 1st perforated plate back cavity thickness h1/mm 35 Helmholtz resonator back cavity thickness dc/mm 8 Helmholtz resonance cavity neck length dn/mm 2 Helmholtz resonant cavity neck radius rn/mm 1 the 2nd perforated plate thickness t2/mm 2.9 the 2nd perforated plate hole diameter d2/mm 1 the 2nd perforated plate back cavity thickness h2/mm 25 the 1st perforated plate perforation rate p1 0.024 7 the 2nd perforated plate perforation rate p2 0.020 4 structural unit cell length L/mm 31 表 2 用于人工神经网络模型训练的MPRSM结构参数取值范围
Table 2. MPRSM structural parameter values for the artificial neural network (ANN) model training
geometric parameter value range the 1st perforated plate thickness t1/mm 0.5~2 the 1st perforated plate hole diameter d1/mm 0.3~1 the 1st perforated plate back cavity thickness h1/mm 5~30 Helmholtz resonator back cavity thickness dc/mm 5~30 Helmholtz resonance cavity neck length dn/mm 1~5 Helmholtz resonant cavity neck radius rn/mm 0.5~2 the 2nd perforated plate thickness t2/mm 0.5~2 the 2nd perforated plate hole diameter d2/mm 0.3~1 the 2nd perforated plate back cavity thickness h2/mm 5~30 表 3 验证人工神经网络模型预测能力的四组结构参数
Table 3. Four sets of structural parameters for verifying the predictive ability of the ANN model
optimization parameter set 1 set 2 set 3 set 4 the 1st perforated plate thickness t1/mm 0.51 1.60 1.41 0.70 the 1st perforated plate hole diameter d1/mm 0.50 0.81 0.90 0.71 the 1st perforated plate back cavity thickness h1/mm 13.89 16.80 25.11 13.20 Helmholtz resonator back cavity thickness dc/mm 28.20 8.21 17.90 25.10 Helmholtz resonance cavity neck length dn/mm 4.10 3.10 3.50 3.70 Helmholtz resonant cavity neck radius rn/mm 0.50 1.21 0.80 0.90 the 2nd perforated plate thickness t2/mm 0.80 1.01 1.50 1.50 the 2nd perforated plate hole diameter d2/mm 0.40 0.80 0.70 0.60 the 2nd perforated plate back cavity thickness h2/mm 24.80 14.19 10.30 28.10 表 4 MPRSM结构优化参数取值范围以及优化结果
Table 4. Range of MPRSM structural optimization parameters and optimization results
optimization parameter value range optimization result the 1st perforated plate thickness t1/mm 0.5~2 0.51 the 1st perforated plate hole diameter d1/mm 0.3~1 0.89 the 1st perforated plate back cavity thickness h1/mm 5~30 27.90 Helmholtz resonator back cavity thickness dc/mm 5~30 29.90 Helmholtz resonance cavity neck length dn/mm 1~5 4.81 Helmholtz resonant cavity neck radius rn/mm 0.5~2 0.50 the 2nd perforated plate thickness t2/mm 0.5~2 0.50 the 2nd perforated plate hole diameter d2/mm 0.3~1 0.41 the 2nd perforated plate back cavity thickness h2/mm 5~30 15.88 -
[1] 郭梦媛, 刘崇锐, 苏文斌, 等. 高阶微穿孔型超材料低频宽带吸声机理[J]. 西安交通大学学报, 2024, 58(4): 192-199, 220. doi: 10.7652/xjtuxb202404018GUO Mengyuan, LIU Chongrui, SU Wengbin, et al. Low-frequency broadband absorption mechanism of high-order micro-perforated meta-materials[J]. Journal of Xi'an Jiaotong University, 2024, 58(4): 192-199, 220. (in Chinese) doi: 10.7652/xjtuxb202404018 [2] MAA D Y. Theory of microslit absorbers[J]. Acta Acustica, 2000, 25(6): 481-485. doi: 10.3321/j.issn:0371-0025.2000.06.001 [3] MAA D Y, LIU K. Sound absorption characteristics of microperforated absorber for random incidence[J]. Acta Acustica, 2000, 25(4): 289-296. [4] LALY Z, ATALLA N, MESLIOUI S A. Acoustical modeling of micro-perforated panel at high sound pressure levels using equivalent fluid approach[J]. Journal of Sound and Vibration, 2018, 427: 134-158. doi: 10.1016/j.jsv.2017.09.011 [5] GAI X L, XING T, LI X H, et al. Sound absorption of microperforated panel with L shape division cavity structure[J]. Applied Acoustics, 2017, 122: 41-50. doi: 10.1016/j.apacoust.2017.02.004 [6] LEE D H, KWON Y P. Estimation of the absorption performance of multiple layer perforated panel systems by transfer matrix method[J]. Journal of Sound and Vibration, 2004, 278(4): 847-860. [7] GAI X L, XING T, LI X H, et al. Sound absorption properties of microperforated panel with membrane cell and mass blocks composite structure[J]. Applied Acoustics, 2018, 137: 98-107. doi: 10.1016/j.apacoust.2018.03.013 [8] LIU X W, YU C L, XIN F X. Gradually perforated porous materials backed with Helmholtz resonant cavity for broadband low-frequency sound absorption[J]. Composite Structures, 2021, 263: 113647. doi: 10.1016/j.compstruct.2021.113647 [9] ZHANG H J, WANG Y, LU K Y, et al. SAP-net: deep learning to predict sound absorption performance of metaporous materials[J]. Materials & Design, 2021, 212: 110156. [10] YANG H T, ZHANG H J, WANG Y, et al. Prediction of sound absorption coefficient for metaporous materials with convolutional neural networks[J]. Applied Acoustics, 2022, 200: 109052. doi: 10.1016/j.apacoust.2022.109052 [11] PAN B R, SONG X, XU J J, et al. Accelerated inverse design of customizable acoustic metaporous structures using a CNN-GA-based hybrid optimization framework[J]. Applied Acoustics, 2023, 210: 109445. [12] IANNACE G, CIABURRO G, TREMATERRA A. Modelling sound absorption properties of broom fibers using artificial neural networks[J]. Applied Acoustics, 2020, 163: 107239. [13] SHEN X M, BAI P F, YANG X C, et al. Low frequency sound absorption by optimal combination structure of porous metal and microperforated panel[J]. Applied Sciences-Basel, 2019, 9(7): 1507. [14] TANG Y F, LI F H, XIN F X, et al. Heterogeneously perforated honeycomb-corrugation hybrid sandwich panel as sound absorber[J]. Materials & Design, 2017, 134: 502-512. [15] TANG Y F, XIN F X, HUANG L X, et al. Deep subwavelength acoustic metamaterial for low-frequency sound absorption[J]. Europhysics Letters, 2017, 118(4): 44002. [16] WANG S B, WANG B, FAN J, et al. Inversion of equivalent parameters of acoustic coating based on genetic algorithm[J]. Journal of Ship Mechanics, 2023, 27(3): 456-469. [17] JIANG Y F, SHEN C, MENG H, et al. Design and optimization of micro-perforated ultralight sandwich structure with N-type hybrid core for broadband sound absorption[J]. Applied Acoustics, 2023, 202: 109184. [18] 王飞萌, 王良模, 王陶, 等. 微穿孔板-三聚氰胺吸音海绵-空腔复合结构声学性能优化设计[J]. 北京化工大学学报(自然科学版), 2022, 49(1): 113-121.WANG Feimeng, WANG Liangmo, WANG Tao, et al. Optimization of the acoustic performance of micro-perforated panel-melamine sound-absorbing sponge-cavity composite structures[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2022, 49(1): 113-121. (in Chinese) [19] LI H X. Fuzzy logic systems are equivalent to feedforward neural networks[J]. Science in China (Series E): Technological Sciences, 2000, 43(1): 42-54. [20] LING S H, LAM H K, LEUNG F H F, et al. A genetic algorithm based neural-tuned neural network[C]//Proceedings of the 29 th Annual Conference of the IEEE Industrial Electronics Society. Roanoke, America, 2003: 2423-2428. [21] WANG X Y, ZHANG Y. Chaotic diagonal recurrent neural network[J]. Chinese Physics B, 2012, 21(3): 038703. [22] WEN L, QIU Z W, QI R N. Passenger capacity prediction based on genetic neural network[C]//Proceedings of the 1 st International Symposium on Information Engineering and Electronic Commerce. Ternopil, Ukraine, 2009: 696-700. [23] 姚浩, 夏桂然, 刘泽佳, 等. 基于机器学习的黏钢构件黏接层缺陷识别方法研究[J]. 应用数学和力学, 2024, 45(4): 429-442.YAO Hao, XIA Guiran, LIU Zejia, et al. A defect identification method for bonding layers of adhesive steel members based on machine learning[J]. Applied Mathematics and Mechanics, 2024, 45(4): 429-442. (in Chinese) [24] CIABURRO G, IANNACE G. Modeling acoustic metamaterials based on reused buttons using data fitting with neural network[J]. Journal of the Acoustical Society of America, 2021, 150(1): 51-63. [25] CIABURRO G, IANNACE G. Membrane-type acoustic metamaterial using cork sheets and attached masses based on reused materials[J]. Applied Acoustics, 2022, 189: 108605. [26] LUO Z H, LI T, YAN Y W, et al. Prediction of sound insulation performance of aramid honeycomb sandwich panel based on artificial neural network[J]. Applied Acoustics, 2022, 190: 108656. [27] DOUTRES O, ATALLA N, OSMAN H. Transfer matrix modeling and experimental validation of cellular porous material with resonant inclusions[J]. Journal of the Acoustical Society of America, 2015, 137(6): 3502-3513. -





 下载:
下载:










 渝公网安备50010802005915号
渝公网安备50010802005915号