低阻抗试样动态加载试验相关问题研究

殷建平; 张晨旭; 孙若恒; 陈希曦; 苗应刚

doi:10.21656/1000-0887.450279

低阻抗试样动态加载试验相关问题研究

doi: 10.21656/1000-0887.450279

殷建平^{1, 2, 3,},
张晨旭^{1, 3, 4},
孙若恒^{1, 3, 4},
陈希曦²,
苗应刚^{1, 3, 4, ,}

1.
陕西省冲击动力学及工程应用重点实验室, 西安 710072
2.
西北工业大学民航学院, 西安 710072
3.
强度与结构完整性全国重点实验室, 西安 710072
4.
西北工业大学航空学院, 西安 710072

基金项目:

国家自然科学基金 12472392

陕西省国际科技合作基金重点项目 2023-GHZD-12

中国航空科学基金 2023-GHZD-12

详细信息

作者简介:
殷建平(1996—)，男，博士生(E-mail: jpyin@mail.nwpu.edu.cn)

通讯作者:
苗应刚(1983—)，男，副教授，博士，硕士生导师(通讯作者. E-mail: ygmiao@nwpu.edu.cn)

中图分类号: O348
计量
- 文章访问数: 100
- HTML全文浏览量: 39
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-21
- 修回日期: 2025-04-10
- 刊出日期: 2025-05-01

Study of Dynamic Loading Tests on Low-Impedance Specimens

YIN Jianping^{1, 2, 3
,},
ZHANG Chenxu^{1, 3, 4},
SUN Ruoheng^{1, 3, 4},
CHEN Xixi²,
MIAO Yinggang^{1, 3, 4
, ,}

1.
Shaanxi Key Laboratory of Impact Dynamics and Engineering Application, Xi'an 710072, P.R.China
2.
School of Civil Aviation, Northwestern Polytechnical University, Xi'an 710072, P.R.China
3.
National Key Laboratory of Strength and Structural Integrity, Xi'an 710072, P.R.China
4.
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, P.R.China

摘要

摘要: 研究了Hopkinson杆开展低阻抗试样高应变率加载测试的关键问题：低阻抗透射信号有效采集和应力平衡问题. 综合前期研究基础，选用异质低阻抗透射杆并辅以原位标定半导体应变片技术，实现低阻抗试样高精度测试；结合应力波加载试样的过程重构计算和分析，获得了低阻抗试样的应力平衡历程和影响因素敏感性特征，并提出了类梯形入射波，可使低阻抗试样尽早实现应力平衡和恒定应变率加载. 研究结果表明：低阻抗有机玻璃杆/管作为透射杆并辅以半导体应变片可实现载荷低至数Newton的透射信号采集；低阻抗试样应力平衡历程依赖于其弹性波速，在类梯形入射波加载下，2倍特征时间上升沿时可实现应力平衡以及其后的恒定应变率加载；其可基于试样厚度设计实现不同应变率加载下的临界有效应变一致性.
- Hopkinson杆 /
- 低阻抗试样 /
- 动态加载 /
- 应力平衡 /
- 透射信号 /
- 高应变率
Abstract: The key problems of the effective acquisition of low-impedance transmitted signals and the stress equilibrium in the Hopkinson bar loading tests on low-impedance specimens with high strain rates, were investigated. Based on the previous research fundaments, low-impedance elastic transmitted bars were introduced to replace the traditional metal transmitted bar, the in-situ calibrated semiconductor strain gauge technology was used to amplify weak transmitted signals, and the low-impedance specimens were tested with high precision. Reconstruction and calculation of the stress wave loading process were conducted to get the stress equilibrium history and the influential factors' sensitivity. The trapezoidal incident wave was proposed to realize stress equilibrium and achieve constant strain rate loading on specimens as early as possible. The results show that, low impedance polymethyl methacrylate bars/tubes as transmitted bars along with semiconductor strain gauges can acquire weak signals as low as several Newtons. The stress equilibrium history of the low-impedance specimen depends on the elastic wave velocity. Under the trapezoidal incident wave loading, the stress equilibrium and constant strain rate loading can be achieved at 2 characteristic periods. Based on the design of specimen thicknesses, the critical effective strain consistency can be achieved under different stress rate loadings.
- Hopkinson bar /
- low-impedance specimen /
- dynamic loading /
- stress equilibrium /
- transmitted signal /
- high strain rate

HTML全文

0. 引言

航空航天等交通运输领域的结构设计过程中，在结构安全及完整性要求下，要考虑材料在动态载荷下力学响应和失效特征等的率效应行为^[1-2]. 而作为缓冲吸能的低阻抗材料，如橡胶缓冲器件、蜂窝或泡沫吸能材料，在现代交通设备中广泛应用^[3-7]. 冲击载荷作用下的吸能特征和作用机理往往不同于准静态下，在设计前需要知悉其动态载荷下的力学响应. 为此，开展低阻抗材料的动态力学性能测试具有重要的工程应用意义，相应作用机理的探究也对相应结构材料设计具有指导意义^[8]. 如橡胶类弹性体材料，具有显著的应变率响应特征，亦即随着加载应变率的提升，其流动应力等力学性能也显著增加，其增量远大于传统工程用金属和复合材料等^[9-11]，且此类材料也表现出韧脆转变特征^[10-11]. 因此，开展低阻抗材料的高精度动态力学性能测试，对认知材料率敏感性、本构响应以及高效安全的工程应用设计具有重要意义^[12-13].

1914年，Hopkinson^[14]设计了细长杆装置，对雷管爆炸所产生的应力波特征进行了测量，成为有文献记载的首次成功采用应力波进行测量的试验. 此后应力波加载技术逐步被改进与创新，现已成为材料动态力学测试的有力手段^[15-19]. 随着抗冲击防护结构的设计需求增加，低阻抗材料的动态力学性能测试和研究方兴未艾. 由于此类材料在动态测试中产生的透射信号微弱，基于透射杆弹性应变信息的高精度采集较为困难，Zhao等^[20]提出了用黏弹性Hopkinson杆测量低阻抗材料的加载技术，重点介绍了弥散修正技术. Chen等^[21]采用铝管作为透射杆输出透射信号，使得透射信号的幅值增强9倍左右. 其后，石英压电晶体的应用^[22-24]更进一步拓展了SHPB可测材料的范围. 此外，为进一步提升低阻抗试样的透射信号强度，具有高灵敏度的半导体应变片也应用于Hopkinson杆技术中，顺利开展了多孔介质、生物组织试样、EPS泡沫、剪切增稠液、明胶等软材料的动态测试^[24-31]. 为确保测试精度，Miao等^[32]提出了原位实时标定技术，实现了半导体应变片不受环境温度影响的高精度解析试样应力信息，先后用于水凝胶和生物肺脏组织材料的动态测试^[33-34].

针对低阻抗试样的动态测试，另一重要问题是如何尽早实现应力平衡加载，这一要求出于Hopkinson杆测试技术的重要假设. 周风华等^[35]采用特征线法详细分析了SHPB测试高聚物时，试样内部早期应力不均匀的产生过程以及其对获得应力-应变曲线的影响，并提出了修正方法. Ravichandran等^[36]在分析高强度陶瓷材料动态试验强度的突变原因中，推导了在应力波加载初期的应力平衡进程，给出了5%的应力平衡评价指标，并提出了极限应变率的概念. 结果显示应力波在试样内来回传播3次之后，试样基本实现了应力平衡. Yang等^[37]详细分析了试样在矩形波、梯形波加载下的应力平衡情况，对比发现，具有一定上升沿的梯形波可以更早实现应力平衡，并预测存在更早实现试样变形均匀的最优加载波. 王礼立等^[38]分析了Hopkinson杆加载试样初期应力平衡的实现过程、试样横向惯性效应的影响，认为用梯形加载波加载试样较为理想. Zhu等^[39]在分析混凝土试样的应力均匀性问题时，发现当梯形波上升沿时间等于应力波在试样内来回传播时间时，试样实现应力平衡，低于或高于来回传播时间时，应力平衡状况都会更糟. 为实现特定波形的应力波加载，Frew等^[40]开展了岩石材料的Hopkinson杆实验，为改善试样内的应力平衡进程，采用了波形整形技术，使试样较早实现了动态应力平衡和恒定应变率加载. 该技术被广泛应用于聚合物动态加载实验、小应变精确测量、低阻抗和软材料的动态力学性能测试和弹塑性材料性能测试^{[13, 17-19, 23-27, 30-34, 40-44]}.

为实现低阻抗试样的动态高应变率有效加载和测试，获得高精度的材料本构响应参数，结合前期研究基础，针对低阻抗试样动态加载的透射信号高精度采集和试样应力平衡历程开展分析和数值重构讨论，相关结果有利于指导该类实验设计和试验结果有效性分析.

1. Hopkinson杆动态加载技术

在材料的高应变率加载技术中，Hopkinson杆技术因其高精度和易操作性被广泛采用. 图 1展示了传统Hopkinson压杆示意图，该系统主要由撞击杆、入射杆和透射杆组成，再配以气炮驱动装置和数据采集设备. 通常情况下，撞击杆、入射杆和透射杆由同种材质的高强度金属材料制成，具有相同的直径.

图 1 传统Hopkinson压杆组成

Figure 1. An illustration for the traditional split Hopkinson pressure bar

下载: 全尺寸图片幻灯片

基于一维应力波理论，根据应变片上采集到的入射波、反射波和透射波，可以推导获得试样的加载工程应变率、工程应变和工程应力，表达式如下：

$\left\{\begin{array}{l} \dot{\varepsilon}_{\text {engi }}(t)=-\frac{2 c_{\mathrm{B}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{r}}, \\ \varepsilon_{\text {engi }}(t)=-\frac{2 c_{\mathrm{B}}}{l_{\mathrm{S}}} \int_{0}^{t} \varepsilon_{\mathrm{r}} \mathrm{~d} t, \\ \sigma_{\text {engi }}(t)=\frac{A_{\mathrm{B}}}{A_{\mathrm{S}}} E_{\mathrm{B}} \varepsilon_{\mathrm{t}}, \end{array}\right.$

(1)

式中，角标r、t分别指代反射、透射；角标B、S分别指代杆、试样；c为波速；ε_r和ε_t分别为反射波和透射波；A，l和E分别为横截面积、长度和弹性模量. 一维弹性波速由材料弹性模量和密度计算获得，如弹性杆的波速由公式 $c_{\mathrm{B}}=\sqrt{E / \rho}$ 计算, 其中r为杆材密度. 基于试样材料的体积不变假设，可以推导获得由工程应变和应力计算得到的真实应变和应力，如下：

$\left\{\begin{array}{l} \varepsilon_{\text {true }}=-\ln \left(1-\varepsilon_{\text {engi }}\right) , \\ \sigma_{\text {true }}=\sigma_{\text {engi }}\left(1-\varepsilon_{\text {engi }}\right). \end{array}\right.$

(2)

对于橡胶类弹性体试样、生物组织试样、纤维束试样以及受制备技术限制获得的小截面尺寸的金属试样，基于此类试样开展动态加载时，试样所产生的载荷较小，在数百Newton(N)量级，甚至低至数Newton量级，在本文中统称为低阻抗试样. 在基于传统Hopkinson杆开展动态压缩或拉伸加载时，变形过程中所产生的动态载荷经由透射杆上的应变片采集. 对于传统的金属材质Hopkinson杆，上述的低阻抗材料产生的透射应变信号十分微弱，甚至被测试系统的干扰信号湮灭，这是低阻抗试样动态测试面临的首要问题^[45-47]. 其次，对于诸多低阻抗试样，如橡胶弹性体、生物组织试样，由于其波速低，导致加载过程中的应力平衡较难实现，最终动态测试的结果可靠性存疑.

2. 低幅值透射信号的采集

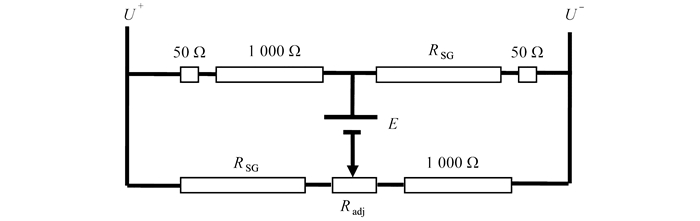
Hopkinson杆加载设备中，弹性杆表面的应变信号幅值高至数千微应变，低至数百微应变量级，导致测量电路的电压变化极小，因此基于Wheatstone电桥的应变信号测量系统发展演化后被广泛采用^[32].

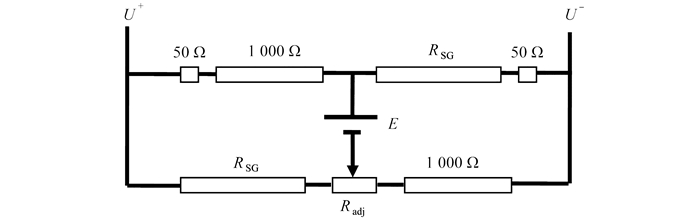
图 2中R_SG指代应变片电阻，R_adj指代平衡调节电阻. 在本文研究中，相应数值分别为1 000 Ω和100 Ω. 针对图 2中Wheatstone电桥，可以推导获得杆上应变片的应变ε与输出电压ΔU、直流电压E、回路电阻R_C和应变片放大系数K的关系，如下：

$\varepsilon=\frac{\Delta U}{E-\Delta U} \cdot \frac{R_{\mathrm{C}}}{K \cdot R_{\mathrm{SG}}} .$

(3)

图 2 用于Hopkinson杆系统应变信号测量的Wheatstone电桥电路图

Figure 2. The Wheatstone bridge circuit for detecting strain signals of the split Hopkinson pressure bar

下载: 全尺寸图片幻灯片

2.1 高灵敏度半导体应用

目前，广泛使用的金属栅丝应变片灵敏度系数K范围在1.92~2.10之间，而更为敏感的半导体应变片系数可以高达150. 表 1列出了应用于图 2中电桥的应变片参数，以及基于同一应变下计算获得的电压输出信号. 其中半导体应变片电阻选用的阻值也为1 000 Ω. 可以发现，针对同一采集应变100 με，金属栅丝和半导体应变片信号输出分别为2.74 mV和213 mV. 若用于电压信号的数据采集设备最低探测精度为2 mV，则金属栅丝应变片采集的最低应变在100 με左右，然而鉴于半导体应变片的高灵敏度优势，对应的应变信号在1 με左右.

表 1 金属栅丝应变片和半导体应变片输出电压信号对比

Table 1. Output signal comparison of the metal grid strain gauge and the semiconductor strain gauge

strain gauge	input voltage /V	resistance /Ω	gain factor	strain /με	output signal /mV
metal grid	30	1 000	150	100	2.74
semiconductor	30	1 000	2.10	100	213

下载: 导出CSV

| 显示表格

基于表 1计算结果对比可知，高灵敏度的半导体应变片在采集和记录透射波信号时具有优势. 但是由于半导体应变片对工作温度的敏感性，其在信号采集过程中，电阻和灵敏度系数会有较大的偏差. 基于式(3)可以发现，获得的应变信号也会随之产生显著的误差，影响了Hopkinson杆动态测试的精度. 为此，Miao等^[32]提出了原位同步标定方案：基于入射杆上粘贴的金属栅丝应变片和半导体应变片同时采集高强度的入射波信号，通过金属栅丝应变片的高精度测试结果标定半导体应变片电阻和灵敏度系数，获得半导体应变片在动态加载过程中的电阻值和灵敏度系数，由于入射杆和透射杆上的半导体应变片工作环境一致，标定获得的参数用于透射波信号的应变信息计算，最后获得高精度的透射信号采集和计算.

2.2 异质透射杆应用

针对低阻抗试样的动态测试，Hopkinson杆多选用同种聚合物材质的入射杆和透射杆^[20]. 为进一步放大透射信号并考虑加载的方便性，可以采用高强度金属质入射杆和聚合物质透射杆的异质Hopkinson杆系统^[27]，该系统不仅可以实现低阻抗透射杆的进一步放大，并且由于入射杆的高强度可以继续开展足够高应变率的加载，另外透射杆应变片靠近试样处粘贴，还可以减弱透射波在聚合物质杆中传播的弥散效应，进而避免了波形弥散修正的繁琐工作.

由于透射杆和入射杆波阻抗的不匹配，在利用入射波、反射波和透射波计算试样应变率、应变和应力过程中，需要重新基于应力波理论推导计算公式，如下：

$\left\{\begin{array} { l } { \dot { \varepsilon } _ { \text { engi } } = \frac { c _ { \mathrm { I } } } { l _ { \mathrm { S } } } \varepsilon _ { \mathrm { i } } - \frac { c _ { \mathrm { I } } } { l _ { \mathrm { S } } } \varepsilon _ { \mathrm { r } } - \frac { c _ { \mathrm { T } } } { l _ { \mathrm { S } } } \varepsilon _ { \mathrm { t } } , } \\ { \varepsilon _ { \text { engi } } = \int _ { 0 } ^ { t } ( \frac { c _ { \mathrm { T } } } { l _ { \mathrm { S } } } \varepsilon _ { \mathrm { i } } - \frac { c _ { \mathrm { T } } } { l _ { \mathrm { S } } } \varepsilon _ { \mathrm { r } } - \frac { c _ { \mathrm { T } } } { l _ { \mathrm { S } } } \varepsilon _ { \mathrm { t } } ) \mathrm { d } t } , \\ { \sigma _ { \text { engi } } = \frac { A _ { \mathrm { T } } E _ { \mathrm { I } } } { 2 A _ { \mathrm { S } } } ( \varepsilon _ { \mathrm { i } } + \varepsilon _ { \mathrm { r } } ) + \frac { A _ { \mathrm { T } } E _ { \mathrm { T } } } { 2 A _ { \mathrm { S } } } \varepsilon _ { \mathrm { t } } , } \end{array} \Rightarrow \left\{\begin{array}{l} \dot{\varepsilon}_{\text {engi }}=\frac{c_{\mathrm{T}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{i}}-\frac{c_{\mathrm{T}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{r}}-\frac{c_{\mathrm{T}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{t}}, \\ \varepsilon_{\text {engi }}=\int_{0}^{t}\left(\frac{c_{\mathrm{T}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{i}}-\frac{c_{\mathrm{T}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{r}}-\frac{c_{\mathrm{T}}}{l_{\mathrm{S}}} \varepsilon_{\mathrm{t}}\right) \mathrm{d} t, \\ \sigma_{\text {engi }}=\frac{A_{\mathrm{T}}}{A_{\mathrm{S}}} E_{\mathrm{T}} \varepsilon_{\mathrm{t}} . \end{array}\right.\right.$

(4)

相应的推导细节以及假设等可参考文献[27].

通过对比式(1)和(4)可以发现，应力正比于透射杆弹性模量. 因此，选用异质的有机玻璃杆作为透射杆，相较于钛合金透射杆，透射应力可探测精度将提高23倍左右(钛合金和有机玻璃弹性模量分别以113 GPa和5 GPa计). 对于更低阻抗试样的动态测试，由于有机玻璃管截面积更小，作为透射输出杆可以进一步放大透射信号，该方案在水凝胶和生物组织试样的动态测试中成功应用^[33-34].

3. 应力平衡分析与优化

Hopkinson杆加载试样过程的应力平衡分析，是基于Ravichandran等^[36]提出的评测方法开展的. 通过计算入射波和反射波获得试样和入射杆界面处的应力σ₁，再基于透射波信号计算获得透射杆和试样界面处的应力σ₂. 结合式(5)定义了应力平衡系数R(t)来定量评价应力平衡历程，并定义了特征时间τ=l_S/c_S, 亦即试样的长度除以试样的波速获得的具有时间量纲的归一化参量. 结合针对脆性陶瓷材料动态测试的分析，提出了R(t)不大于5%来定义试样已经进入应力平衡变形的评价建议，后被广泛采用. 在分析低阻抗试样动态加载时，基于微弱透射信号计算出的σ₂较小，而入射波或反射波应力较大，甚至高出1~2个数量级. 因此通过入射波和反射波相加获得的应力σ₁，其信号采集误差基本和σ₂在一个数量级，难以实现足够精确的应力平衡比较和分析：

$R(t)=\frac{\left|\sigma_{1}-\sigma_{2}\right|}{\left(\sigma_{1}+\sigma_{2}\right) / 2}.$

(5)

3.1 应力平衡历程分析

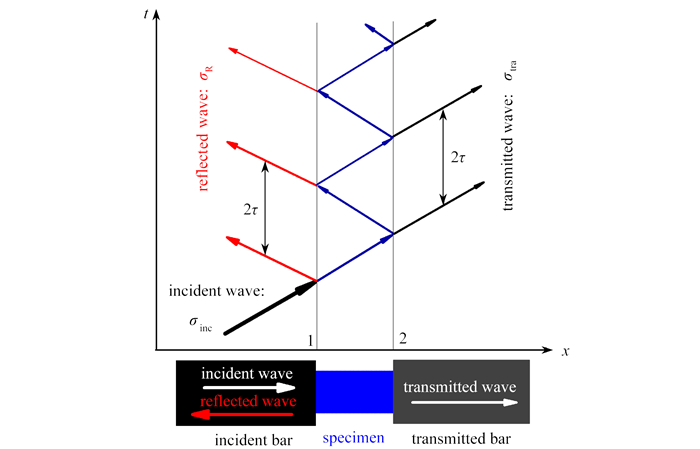
通过对应力波加载试样过程的重构，并开展具有针对性的分析，可以从机理上探究应力平衡历程以及相关因素影响敏感性特征. 该重构过程基于一维应力波传播原理，在试样夹持段开展一列入射波加载下的系列反射和透射波过程重构^{[43, 45-47]}，具体示意图如图 3所示. 在入射杆和试样界面处反射形成的系列反射波叠加后即为反射波，透射波同理.

图 3 应力波加载试样时反射和透射波形

Figure 3. The series of reflected and transmitted waves for a stress wave loading on the specimen

下载: 全尺寸图片幻灯片

应力波在不同波阻抗界面处产生反射和透射，基于一维应力波理论发现，反射和透射系数依赖于两界面的阻抗和面积特征. 用F和T分别表示反射和透射系数，下角标表示应力波进入不同界面的顺序，如T_BS表示应力波从杆进入试样的透射系数. 结合图 3中多界面反射和透射需要，列出了如下系数和定义参数:

$\left\{\begin{array}{l} T_{\mathrm{BS}}=\frac{2 \alpha_{\mathrm{BS}}}{1+n_{\mathrm{BS}}}, F_{\mathrm{BS}}=\frac{1-n_{\mathrm{BS}}}{1+n_{\mathrm{BS}}}, \\ T_{\mathrm{SB}}=\frac{2 n_{\mathrm{BS}}}{n_{\mathrm{BS}} \alpha_{\mathrm{BS}}+\alpha_{\mathrm{BS}}}, F_{\mathrm{SB}}=\frac{n_{\mathrm{BS}}-1}{n_{\mathrm{BS}}+1}, \\ n_{\mathrm{BS}}=\frac{(\rho c A)_{\mathrm{B}}}{(\rho c A)_{\mathrm{S}}}, \alpha_{\mathrm{BS}}=\frac{A_{\mathrm{B}}}{A_{\mathrm{S}}}, \\ \end{array}\right.$

(6a)

$\left\{\begin{array}{l} T_{\mathrm{TS}}=\frac{2 \alpha_{\mathrm{TS}}}{1+n_{\mathrm{TS}}}, F_{\mathrm{TS}}=\frac{1-n_{\mathrm{TS}}}{1+n_{\mathrm{TS}}}, \\ T_{\mathrm{ST}}=\frac{2 n_{\mathrm{TS}}}{n_{\mathrm{TS}} \alpha_{\mathrm{TS}}+\alpha_{\mathrm{TS}}}, F_{\mathrm{ST}}=\frac{n_{\mathrm{TS}}-1}{n_{\mathrm{TS}}+1}, \\ n_{\mathrm{TS}}=\frac{(\rho c A)_{\mathrm{T}}}{(\rho c A)_{\mathrm{S}}}, \alpha_{\mathrm{TS}}=\frac{A_{\mathrm{T}}}{A_{\mathrm{S}}} . \end{array}\right.$

(6b)

结合重构过程分别计算获得反射波和透射波，进而获得σ₁和σ₂. 代入式(7)获得应力波加载试样的历程特征：

$\left\{\begin{array}{l} \sigma_{\mathrm{ref}}(t)=\sigma_{\mathrm{inc}}(t) \cdot F_{\mathrm{BS}}+\sigma_{\mathrm{inc}}(t-2 \tau) \cdot T_{\mathrm{BS}} \cdot F_{\mathrm{ST}} \cdot T_{\mathrm{SB}}+ \\ \quad \sigma_{\mathrm{inc}}(t-4 \tau) \cdot T_{\mathrm{BS}} \cdot F_{\mathrm{ST}}^{2} \cdot F_{\mathrm{SB}}^{1} \cdot T_{\mathrm{SB}}+\cdots, \\ \sigma_{1}(t)=\sigma_{\mathrm{inc}}(t)+\sigma_{\mathrm{ref}}(t)= \\ \quad \sigma_{\mathrm{inc}}(t)+\sigma_{\mathrm{inc}}(t) \cdot F_{\mathrm{BS}}+\sigma_{\mathrm{inc}}(t-2 \tau) \cdot T_{\mathrm{BS}} \cdot F_{\mathrm{ST}} \cdot T_{\mathrm{SB}}+ \\ \quad \sigma_{\mathrm{inc}}(t-4 \tau) \cdot T_{\mathrm{BS}} \cdot F_{\mathrm{ST}}^{2} \cdot F_{\mathrm{SB}}^{1} \cdot T_{\mathrm{SB}}+\cdots, \\ \sigma_{2}(t)=\sigma_{\mathrm{tra}}(t)=\sigma_{\mathrm{inc}}(t-\tau) \cdot T_{\mathrm{BS}} \cdot T_{\mathrm{ST}}+\sigma_{\mathrm{inc}}(t-3 \tau) \cdot T_{\mathrm{BS}} \cdot F_{\mathrm{SB}} \cdot F_{\mathrm{ST}} \cdot T_{\mathrm{SB}}+ \\ \quad \sigma_{\mathrm{inc}}(t-5 \tau) \cdot T_{\mathrm{BS}} \cdot F_{\mathrm{SB}}^{2} \cdot F_{\mathrm{ST}}^{2} \cdot T_{\mathrm{SB}}+\cdots . \end{array}\right.$

(7)

针对低阻抗试样的改进型Hopkinson压杆测试系统，采用低阻抗有机玻璃杆PMMA杆作为透射杆，入射杆选用高强度钢，相应的尺寸和力学参数见表 2. 为研究应力平衡历程对波阻抗比的依赖性，针对同质透射杆和橡胶、钛合金试样进行了应力波加载初期的应力平衡历程分析，相关参数见表 2.

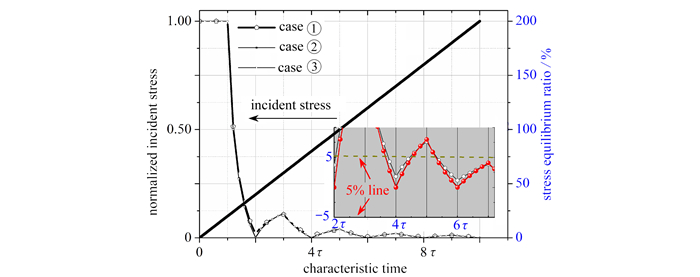
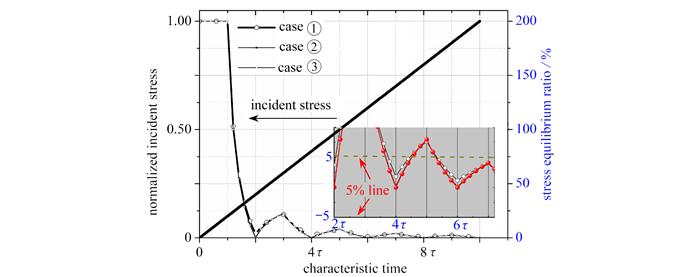
表 2 改进型Hopkinson杆和试样尺寸与力学参数

Table 2. Dimensions and mechanic parameters of the modified SHPBs and specimens

	incident bar(steel)	specimen(rubber)	specimen(TC4)	transmitted bar(steel)	transmitted bar(PMMA)
diameter /mm	19	5	5	19	8
length or thickness /mm	3 100	5	5	3 100	1 000
elastic modulus /MPa	210 000	1	113 000	210 000	5 000
density /(kg/m³)	8 060	900	4 560	8 060	1 200
wave speed /(m/s)	5 104	33.33	4 978	5 104	2 041
specific impedance ratio	19 803	1	757	19 803	209

下载: 导出CSV

| 显示表格

本文分别开展了三种典型工况下的应力平衡历程重构计算和分析：①钢质入射杆、透射杆加载钛合金试样；②钢质入射杆、PMMA透射杆加载橡胶试样；③钢质入射杆、透射杆加载橡胶试样. 在同一列斜坡应力波加载下的应力平衡曲线如图 4所示，其中横轴为归一化后的特征时间，局部放大图展示了在2~7倍特征时间内应力平衡历程的对比. 在线性斜坡加载下，在2倍特征时间后，应力平衡曲线随加载时间振荡性地衰减，在6τ后进入±5%区域范围内，完全进入了应力平衡变形过程. 其趋势和Ravichandran等的研究结果一致^{[36, 43, 45-47]}.

图 4 SHPB中斜坡加载下试样应力平衡变化

Figure 4. The stress equilibrium variations of the specimens under the ramp loading in SHPBs

下载: 全尺寸图片幻灯片

上述三种工况的应力平衡历程曲线几乎一致，在数值上稍有差别，这主要缘于试样和透射杆的波阻抗比. 由表 2可以发现，工况①、②和③的透射杆和试样波阻抗比依次增加，其应力平衡参数也降至最低. 因此，实现应力平衡的加载历程，在线性斜坡加载下的6倍特征时间，试样进入完全的应力平衡变形阶段. 在研究的低阻抗测试系统中，试样与透射杆阻抗比对应力平衡历程影响可以忽略. 因此，应力平衡历程依赖于加载时间或特征时间τ，与波阻抗比几乎无关.

3.2 入射波优化

应力平衡的实现历程依赖于加载时间，在线性斜坡加载下6倍特征时间后方能完全进入应力平衡变形. 对于典型的金属试样加载，由于其波速较高，特征时间在1~2 μs左右，应力平衡在10 μs之内基本能顺利实现. 基于传统的撞击杆撞击产生的梯形入射波，其上升沿时间也在10 μs量级，即在上升沿阶段基本上实现了试样的应力平衡加载. 而对于低波速试样，尤其是橡胶试样甚至生物组织试样，其波速较低，如表 2中的橡胶试样其波速低至33.3 m/s，相应的特征时间为150 μs，按照斜坡加载下的6倍特征时间计算，橡胶试样需要900 μs的上升沿时间方能实现应力平衡加载，如此长的加载脉宽远超出了Hopkinson杆加载脉宽. 因此如何更早实现应力平衡加载，对低波速试样的有效动态高应变率加载至关重要.

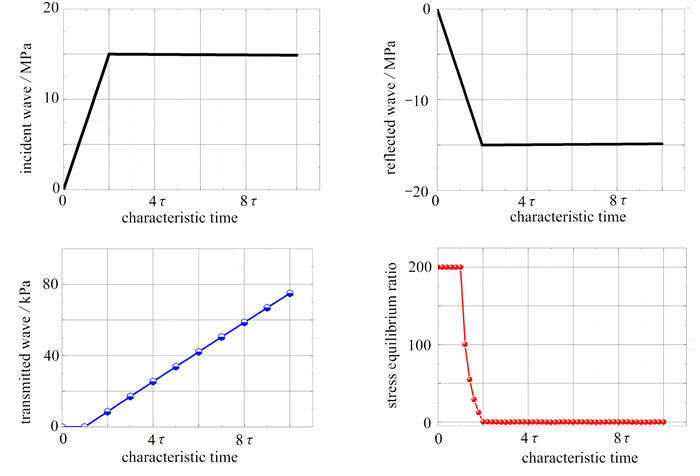
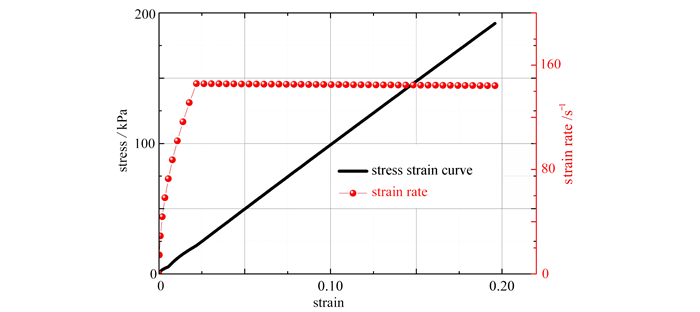
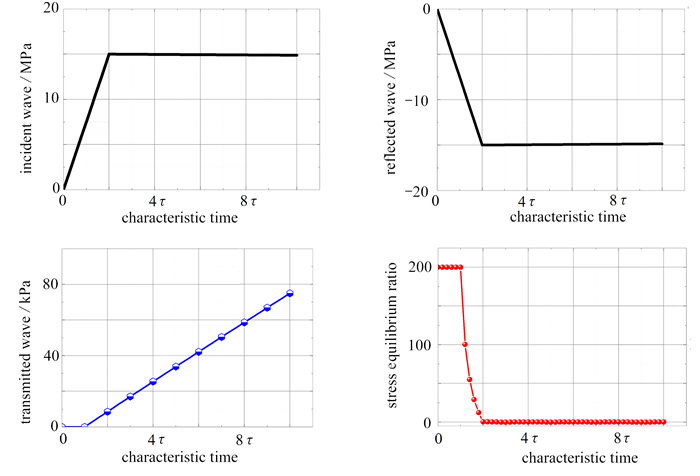
前期针对高强度脆性陶瓷材料开展了加载入射波的优化研究^[43]，提出了在2倍特征时间之后实现恒定应变率加载和进入应力平衡的入射波理论解析解，通过降低在2τ之后的入射波斜率，由线性斜坡加载转变为双线性应力波加载. 并通过脆性砂岩材料的动态压缩加载实验验证了该双线性波的优势. 结合低阻抗试样动态加载Hopkinson杆系统的加载特点，提出了类梯形入射波加载构型：上升沿时间为2倍特征时间，其后加载波保持近乎恒定幅值. 该波形可实现等同于类陶瓷材料的双线性波加载的优势. 结合表 2中工况②的参数开展应力波加载重构计算，计算结果如图 5所示，其分别展示了类梯形加载入射波、所产生的反射波和透射波以及计算获得的应力平衡系数随加载特征时间的变化趋势. 可以发现在2τ之后，应力平衡系数进入5%之内，之后随加载时间持续增大，该系数不再明显衰减振荡变化，而是持续地维持在5%之内. 而线性斜坡加载需要6τ时长的应力平衡. 相对于上述估算的橡胶试样，其应力平衡时间缩短为300 μs，这在实验室条件下是可行的. 图 6展示了重构计算获得的应力-应变曲线以及对应的应变率曲线. 在2τ时刻时，试样的变形积累应变为0.021 9，并进入恒定应变率变形阶段. 这展示了类梯形加载波的另一优势：可以更早地在2τ后实现恒定应变率加载. 在实际实验过程中，很难精确地在2τ时刻实现应力波斜率转折的类梯形加载波，经过类似的应力波重构计算发现：只要上升沿时间不低于2τ时间，该类梯形波的优势仍然存在，亦即在应力波斜率转折时实现应力平衡，之后进入恒定应变率加载阶段.

图 5 类梯形入射波及其反射波、透射波和应力平衡系数随加载时间变化

Figure 5. The trapezoidal incident wave and its reflected wave, transmitted wave and stress equilibrium ratio varying with the loading time

下载: 全尺寸图片幻灯片

图 6 基于波形重构得到的应力-应变曲线与应变率-应变曲线

Figure 6. The stress-strain curve and strain rate-strain curve obtained based on waveform reconstruction

下载: 全尺寸图片幻灯片

3.3 有效应变分析

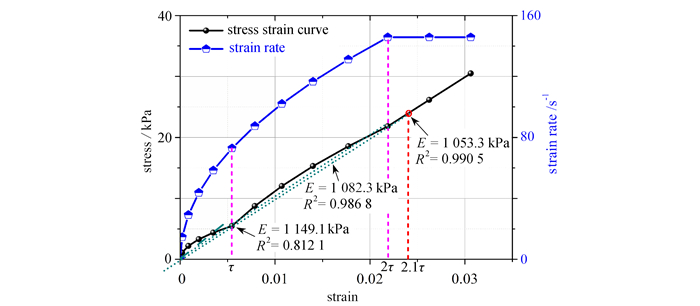
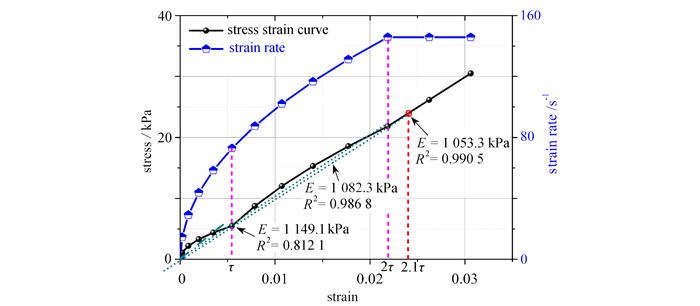
在应力波加载试样的初始阶段，加载应变率从0逐渐增加至设计的应变率. 这一过程的应变率并不恒定. 图 7展示了图 6中重构的应变率曲线和应力-应变曲线的初始阶段(0~2.4τ)，并分别拟合获得了0~1τ，0~2τ和0~2.1τ加载时段内的重构应力-应变曲线的弹性模量. 对比发现，相对于输入的弹性模量1 000 MPa，基于重构结果获得的弹性模量误差分别为14.91%，8.23%和5.33%，随着加载时长的增加误差越来越小，更加趋近于输入值，而且拟合的曲线线性度也逐渐趋近于R²=1.000.因此可以得出结论：在2τ的加载时间内，获得应力-应变曲线存在误差，这主要源于加载期间的应力或应变不均匀变形. 因此，建议以2τ时刻所产生的应变为临界有效应变.

图 7 双线性波加载下试样临界有效应变的确定

Figure 7. The determination of the critical effective strain of the specimen under biaxial wave loading

下载: 全尺寸图片幻灯片

临界有效应变的估算，可以基于式(8)计算获得：

$\varepsilon_{\text {eff }}=\int_{0}^{2 \tau} \dot{\varepsilon}(t) \mathrm{d} t .$

(8)

为获得更多有效的实验数据，针对低阻抗试样开展动态加载时，上述提出的类梯形加载波具有两重优势：可以在2τ时刻内实现应力平衡加载；其后进入恒定应变率加载. 关于有效应变分析将基于上述加载入射波的前提进行. 基于式(8)可以发现，应变率历程均是从0快速增加至设计的加载应变率，而这一过程对有效应变的影响最大. 因此，如何降低2τ时间长度，对降低临界有效应变具有重要作用. 数值上其由试样长度决定，因此在开展动态实验设计中，在更高应变率加载时降低试样厚度，可以实现在相应更高动态应变率加载的同时，还能保证临界有效应变不至于随之增高. 对比类似研究结果^{[13, 43, 45-47]}，在2τ加载时间内，试样变形的应变率历程特征几乎一致，因此临界有效应变正比于特征时间. 当试样厚度按比例降低时，在同样的加载波作用下，应变率也将按比例增高，进而实现更高应变率加载同时保证一致的有效应变. 这有利于后续的材料力学响应对比分析.

4. 结论

本文研究了Hopkinson杆开展低阻抗试样高应变率加载测试的两个关键问题，分析讨论了微弱透射信号采集策略，并结合应力波加载重构定量分析和讨论了低阻抗试样动态加载的应力平衡历程及其影响因素，提出了优化的类梯形加载波，也验证了其优势. 相关结论如下：

1) 选用异质低阻抗透射杆并辅以原位标定半导体应变片技术，实现低阻抗试样高精度测试，最低探测载荷可达数Newton量级；

2) 低阻抗试样的应力平衡历程依赖于试样材料波速或特征时间，与波阻抗比值无关；

3) 上升沿时长为2τ的类梯形入射波可使低阻抗试样在2τ内实现应力平衡，以及恒定应变率加载；

4) 提出了临界有效应变概念，通过设计不同厚度试样实现不同应变率加载下一致的临界有效应变.

图 1 传统Hopkinson压杆组成

Figure 1. An illustration for the traditional split Hopkinson pressure bar

下载: 全尺寸图片幻灯片

图 2 用于Hopkinson杆系统应变信号测量的Wheatstone电桥电路图

Figure 2. The Wheatstone bridge circuit for detecting strain signals of the split Hopkinson pressure bar

下载: 全尺寸图片幻灯片

图 3 应力波加载试样时反射和透射波形

Figure 3. The series of reflected and transmitted waves for a stress wave loading on the specimen

下载: 全尺寸图片幻灯片

图 4 SHPB中斜坡加载下试样应力平衡变化

Figure 4. The stress equilibrium variations of the specimens under the ramp loading in SHPBs

下载: 全尺寸图片幻灯片

图 5 类梯形入射波及其反射波、透射波和应力平衡系数随加载时间变化

Figure 5. The trapezoidal incident wave and its reflected wave, transmitted wave and stress equilibrium ratio varying with the loading time

下载: 全尺寸图片幻灯片

图 6 基于波形重构得到的应力-应变曲线与应变率-应变曲线

Figure 6. The stress-strain curve and strain rate-strain curve obtained based on waveform reconstruction

下载: 全尺寸图片幻灯片

图 7 双线性波加载下试样临界有效应变的确定

Figure 7. The determination of the critical effective strain of the specimen under biaxial wave loading

下载: 全尺寸图片幻灯片

表 1 金属栅丝应变片和半导体应变片输出电压信号对比

Table 1. Output signal comparison of the metal grid strain gauge and the semiconductor strain gauge

strain gauge	input voltage /V	resistance /Ω	gain factor	strain /με	output signal /mV
metal grid	30	1 000	150	100	2.74
semiconductor	30	1 000	2.10	100	213

下载: 导出CSV

表 2 改进型Hopkinson杆和试样尺寸与力学参数

Table 2. Dimensions and mechanic parameters of the modified SHPBs and specimens

	incident bar(steel)	specimen(rubber)	specimen(TC4)	transmitted bar(steel)	transmitted bar(PMMA)
diameter /mm	19	5	5	19	8
length or thickness /mm	3 100	5	5	3 100	1 000
elastic modulus /MPa	210 000	1	113 000	210 000	5 000
density /(kg/m³)	8 060	900	4 560	8 060	1 200
wave speed /(m/s)	5 104	33.33	4 978	5 104	2 041
specific impedance ratio	19 803	1	757	19 803	209

下载: 导出CSV

参考文献(47)

[1]	张龙辉, 张晓晴, 姚小虎, 等. 高应变率下航空透明聚氨酯的动态本构模型[J]. 爆炸与冲击, 2015, 35 (1): 51-56. ZHANG Longhui, ZHANG Xiaoqing, YAO Xiaohu, et al. Constitutive model of transparent aviation polyurethane at high strain rates[J]. Explosion and Shock Waves, 2015, 35 (1): 51-56. (in Chinese)
[2]	许泽建, 丁晓燕, 张炜琪, 等. 一种用于材料高应变率剪切性能测试的新型加载技术[J]. 力学学报, 2016, 48 (3): 654-659. XU Zejian, DING Xiaoyan, ZHANG Weiqi, et al. A new loading technique for measuring shearing properties of materials under high strain rates[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48 (3): 654-659. (in Chinese)
[3]	张方举, 何鹏, 胡文军, 等. 软材料的低阻抗SHPB实验技术与应用[J]. 中国测试, 2012, 38 (2): 17-20. ZHANG Fangju, HE Peng, HU Wenjun, et al. Application and experimental technique of low impedance SHPB for soft materials[J]. China Measurement & Test, 2012, 38 (2): 17-20. (in Chinese)
[4]	章超, 徐松林, 王鹏飞. 基于数字图像相关方法对冲击载荷下泡沫铝全场变形过程的测试[J]. 实验力学, 2013, 28 (5): 629-634. ZHANG Chao, XU Songlin, WANG Pengfei. Test of aluminum foam deforming process under impact load based on digital image correlation method[J]. Journal of Experimental Mechanics, 2013, 28 (5): 629-634. (in Chinese)
[5]	HOU B, WANG Y, TANG Z B, et al. The mechanical behaviors of corrugated sandwich panel under quasi-static and dynamic shear-compressive loadings[J]. International Journal of Impact Engineering, 2021, 156 : 103956. doi: 10.1016/j.ijimpeng.2021.103956
[6]	周睿, 张志家, 张旺, 等. 多壁管增强泡沫铝结构动态响应及吸能性能研究[J]. 应用数学和力学, 2024, 45 (1): 12-24. doi: 10.21656/1000-0887.440186 ZHOU Rui, ZHANG Zhijia, ZHANG Wang, et al. Dynamic response and energy absorption performances of multi-walled tube reinforced aluminum foam structure[J]. Applied Mathematics and Mechanics, 2024, 45 (1): 12-24. (in Chinese) doi: 10.21656/1000-0887.440186
[7]	范志庚, 万强, 牛红攀, 等. 计及时变演化特征的硅泡沫垫层非线性黏弹性模型研究[J]. 应用数学和力学, 2024, 45 (2): 167-174. doi: 10.21656/1000-0887.440249 FAN Zhigeng, WAN Qiang, NIU Hongpan, et al. A nonlinear viscoelastic model for silicon rubber foam cushion considering time-varying evolution characteristics[J]. Applied Mathematics and Mechanics, 2024, 45 (2): 167-174. (in Chinese) doi: 10.21656/1000-0887.440249
[8]	MIAO Y G, ZHANG H N, HE H, et al. Mechanical behaviors and equivalent configuration of a polyurea under wide strain rate range[J]. Composite Structures, 2019, 222 : 110923. doi: 10.1016/j.compstruct.2019.110923
[9]	高宁, 朱志武. 铝合金应变率效应综述及其机理研究[J]. 应用数学和力学, 2014, 35 (S1): 208-212. GAO Ning, ZHU Zhiwu. Study on the strain rate effects and mechanisms for aluminum alloys[J]. Applied Mathematics and Mechanics, 2014, 35 (S1): 208-212. (in Chinese)
[10]	CHEN C Y, ZHANG C, LIU C L, et al. Rate-dependent tensile failure behavior of short fiber reinforced PEEK[J]. Composites (Part B): Engineering, 2018, 136 : 187-196. doi: 10.1016/j.compositesb.2017.10.031
[11]	QIN D Y, MIAO Y G, LI Y L. Formation of adiabatic shearing band for high-strength Ti-5553 alloy: a dramatic thermoplastic microstructural evolution[J]. Defence Technology, 2022, 18 (11): 2045-2051. doi: 10.1016/j.dt.2022.06.010
[12]	MIAO Y G, DU W X, YIN J P, et al. Characterizing multi mechanical behaviors for epoxy-like materials under wide strain rate range[J]. Polymer Testing, 2022, 116 : 107804. doi: 10.1016/j.polymertesting.2022.107804
[13]	WU Z B, YIN J P, LI M, et al. Rate-dependent constitutive behavior and mechanism of CMDB under tension loading[J]. Polymer Testing, 2024, 140 : 108584. doi: 10.1016/j.polymertesting.2024.108584
[14]	HOPKINSON B. A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets[J]. Proceedings of the Royal Society of London (Series A), 1914, 89 (612): 411-413.
[15]	MIYAMBO M E, VON KALLON D V, PANDELANI T, et al. Review of the development of the split Hopkinson pressure bar[J]. Procedia CIRP, 2023, 119 : 800-808. doi: 10.1016/j.procir.2023.04.010
[16]	WANG L L. Foundations of Stress Waves[M]. Amsterdam: Elsevier, 2007: 43-49, 65-70.
[17]	CHEN W, SONG B. Split Hopkinson (Kolsky) Bar Design, Testing and Applications[M]. New York: Springer, 2010: 37-51.
[18]	卢芳云, 陈荣, 林玉亮, 等. 霍普金森杆实验技术[M]. 北京: 科学出版社, 2013: 23-52. LU Fangyun, CHEN Rong, LIN Yuliang, et al. Hopkinson Bar Techniques[M]. Beijing: Science Press, 2013: 23-52. (in Chinese)
[19]	胡时胜. Hopkinson压杆实验技术的应用进展[J]. 实验力学, 2005, 20 (4): 589-594. doi: 10.3969/j.issn.1001-4888.2005.04.016 HU Shisheng. The application development of experimental technique of Hopkinson pressure bar[J]. Journal of Experimental Mechanics, 2005, 20 (4): 589-594. (in Chinese) doi: 10.3969/j.issn.1001-4888.2005.04.016
[20]	ZHAO H, GARY G, KLEPACZKO J R. On the use of a viscoelastic split Hopkinson pressure bar[J]. International Journal of Impact Engineering, 1997, 19 (4): 319-330. doi: 10.1016/S0734-743X(96)00038-3
[21]	CHEN W, ZHANG B, FORRESTAL M J. A split Hopkinson bar technique for low-impedance materials[J]. Experimental Mechanics, 1999, 39 : 81-85. doi: 10.1007/BF02331109
[22]	CHEN W, LU F, ZHOU B. A quartz-crystal-embedded split Hopkinson pressure bar for soft materials[J]. Experimental Mechanics, 2000, 40 (1): 1-6. doi: 10.1007/BF02327540
[23]	SONG B, CHEN W, JIANG X. Split Hopkinson pressure bar experiments on polymeric foams[J]. International Journal of Vehicle Design, 2005, 37 (2/3): 185-198. doi: 10.1504/IJVD.2005.006656
[24]	YIN J P, MIAO Y G, WU Z B, et al. A novel Hopkinson tension bar system for testing polymers under intermediate strain rate and large deformation[J]. International Journal of Impact Engineering, 2025, 198 : 105197. doi: 10.1016/j.ijimpeng.2024.105197
[25]	王宝珍, 郑宇轩, 胡时胜. 猪后腿肌肉的动态拉伸性能[J]. 爆炸与冲击, 2010, 30 (5): 449-455. WANG Baozhen, ZHENG Yuxuan, HU Shisheng. Dynamic tensile properties of porcine ham muscle[J]. Explosion and Shock Waves, 2010, 30 (5): 449-455. (in Chinese)
[26]	徐沛保, 巫绪涛, 李和平. 中高应变率下EPS泡沫的冲击压缩实验[J]. 实验力学, 2012, 27 (4): 480-485. XU Peibao, WU Xutao, LI Heping. Impact compression experiment for EPS foam under mid-high strain rate[J]. Journal of Experimental Mechanics, 2012, 27 (4): 480-485. (in Chinese)
[27]	MIAO Y G, LI Y L, DENG Q, et al. Investigation on experimental method of low-impedance materials using modified Hopkinson pressure bar[J]. Journal of Beijing Institute of Technology, 2015, 24 (2): 269-276.
[28]	周永康, 陈力, 崔世堂. 一种新型软材料动态直接拉伸实验技术[J]. 振动与冲击, 2017, 36 (22): 144-148. ZHOU Yongkang, CHEN Li, CUI Shitang. An improved SHTB experimental facility for soft material[J]. Journal of Vibration and Shock, 2017, 36 (22): 144-148. (in Chinese)
[29]	鲍振宇, 温垚珂, 韩瑞国, 等. 弹道明胶的动态力学测试方法研究[J]. 中国测试, 2019, 45 (9): 33-37. BAO Zhenyu, WEN Yaoke, HAN Ruiguo, et al. Study on dynamic mechanical testing method of ballistic gelatin[J]. China Measurement & Test, 2019, 45 (9): 33-37. (in Chinese)
[30]	XU P D, TANG L Q, ZHANG Y R, et al. SHPB experimental method for ultra-soft materials in solution environment[J]. International Journal of Impact Engineering, 2022, 159 : 104051. doi: 10.1016/j.ijimpeng.2021.104051
[31]	WEN Y K, XU L, CHEN A J, et al. Dynamic compressive response of porcine muscle measured using a split Hopkinson bar system with a pair of PVDF force transducers[J]. Defence Technology, 2023, 28 : 298-305. doi: 10.1016/j.dt.2022.08.011
[32]	MIAO Y, GOU X, SHEIKH M Z. A technique for in situ calibration of semiconductor strain gauges used in Hopkinson bar tests[J]. Experimental Techniques, 2018, 42 : 623-629. doi: 10.1007/s40799-018-0283-9
[33]	ZHANG J X, MIAO Y G, QIN Q H, et al. Static and dynamic experiments on hydrogels: effects of the chemical composition of the fluid[J]. Mechanics of Materials, 2021, 154 : 103717. doi: 10.1016/j.mechmat.2020.103717
[34]	LIU Y, DENG Q, WANG Y S, et al. Dynamic mechanical response and functional mechanisms in rabbit pulmonary tissue[J]. Mechanics of Time-Dependent Materials, 2024, 28 (4): 2921-2936. doi: 10.1007/s11043-024-09697-1
[35]	周风华, 王礼立, 胡时胜. 高聚物SHPB试验中试件早期应力不均匀性的影响[J]. 实验力学, 1992, 7 (1): 23-29. ZHOU Fenghua, WANG Lili, HU Shisheng. On the effect of stress nonuniformness in polymer specimen of SHPB tests[J]. Journal of Experimental Mechanics, 1992, 7 (1): 23-29. (in Chinese)
[36]	RAVICHANDRAN G, SUBHASH G. Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar[J]. Journal of the American Ceramic Society, 1994, 77 (1): 263-267. doi: 10.1111/j.1151-2916.1994.tb06987.x
[37]	YANG L M, SHIM V P W. An analysis of stress uniformity in split Hopkinson bar test specimens[J]. International Journal of Impact Engineering, 2005, 31 (2): 129-150. doi: 10.1016/j.ijimpeng.2003.09.002
[38]	王礼立, 王永刚. 应力波在用SHPB研究材料动态本构特性中的重要作用[J]. 爆炸与冲击, 2005, 25 (1): 17-25. WANG Lili, WANG Yonggang. The important role of stress waves in the study on dynamic constitutive behavior of materials by SHPB[J]. Explosion and Shock Waves, 2005, 25 (1): 17-25. (in Chinese)
[39]	ZHU J, HU S, WANG L. An analysis of stress uniformity for concrete-like specimens during SHPB tests[J]. International Journal of Impact Engineering, 2009, 36 (1): 61-72. doi: 10.1016/j.ijimpeng.2008.04.007
[40]	FREW D J, FORRESTAL M J, CHEN W. A split Hopkinson pressure bar technique to determine compressive stress-strain data for rock materials[J]. Experimental Mechanics, 2001, 41 (1): 40-46. doi: 10.1007/BF02323102
[41]	徐明利, 张若棋, 王悟, 等. 波形整形器在酚醛树脂的霍普金森压杆实验中的应用[J]. 爆炸与冲击, 2002, 22 (4): 377-380. doi: 10.3321/j.issn:1001-1455.2002.04.017 XU Mingli, ZHANG Ruoqi, WANG Wu, et al. Application of wave shaper in SHPB experimental study of phenolic resin[J]. Explosion and Shock Waves, 2002, 22 (4): 377-380. (in Chinese) doi: 10.3321/j.issn:1001-1455.2002.04.017
[42]	SONG B, CHEN W. Dynamic stress equilibration in split Hopkinson pressure bar tests on soft materials[J]. Experimental Mechanics, 2004, 44 (3): 300-312. doi: 10.1007/BF02427897
[43]	MIAO Y G. On loading ceramic-like materials using split Hopkinson pressure bar[J]. Acta Mechanica, 2018, 229 (8): 3437-3452. doi: 10.1007/s00707-018-2166-7
[44]	LIU L T, DENG Q, WANG R F, et al. Dynamic enhancement induced by interface for additively manufactured continuous carbon fiber reinforced composites[J]. Polymer Testing, 2024, 132 : 108382. doi: 10.1016/j.polymertesting.2024.108382
[45]	YIN J P, ZHANG C X, SUN R H, et al. Controllable kilohertz impact fatigue loading functioned by cyclic stress wave of Hopkinson tension bar and its application for TC4 titanium alloy[J]. International Journal of Fatigue, 2025, 194 : 108828. doi: 10.1016/j.ijfatigue.2025.108828
[46]	ZHANG C X, SUN R H, YIN J P, et al. Failure behaviours of steel/aluminium threaded connections under impact fatigue[J]. Engineering Failure Analysis, 2025, 174 : 109473. doi: 10.1016/j.engfailanal.2025.109473
[47]	MIAO Y G, LI Y L, LIU H Y, et al. Determination of dynamic elastic modulus of polymeric materials using vertical split Hopkinson pressure bar[J]. International Journal of Mechanical Sciences, 2016, 108/109 : 188-196. doi: 10.1016/j.ijmecsci.2016.02.005

施引文献

资源附件(0)

访问统计

图(7) / 表(2)

计量

文章访问数: 100
HTML全文浏览量: 39
PDF下载量: 17
被引次数: 0

0. 引言
1. Hopkinson杆动态加载技术
2. 低幅值透射信号的采集
2.1 高灵敏度半导体应用
2.2 异质透射杆应用
3. 应力平衡分析与优化
3.1 应力平衡历程分析
3.2 入射波优化
3.3 有效应变分析
4. 结论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

低阻抗试样动态加载试验相关问题研究

doi: 10.21656/1000-0887.450279

作者简介:
殷建平(1996—)，男，博士生(E-mail: jpyin@mail.nwpu.edu.cn)

通讯作者:
苗应刚(1983—)，男，副教授，博士，硕士生导师(通讯作者. E-mail: ygmiao@nwpu.edu.cn)

计量

Study of Dynamic Loading Tests on Low-Impedance Specimens

0. 引言

1. Hopkinson杆动态加载技术

2. 低幅值透射信号的采集

2.1 高灵敏度半导体应用

2.2 异质透射杆应用

3. 应力平衡分析与优化

3.1 应力平衡历程分析

3.2 入射波优化

3.3 有效应变分析

4. 结论

计量

目录

0. 引言

1. Hopkinson杆动态加载技术

2. 低幅值透射信号的采集

2.1 高灵敏度半导体应用

2.2 异质透射杆应用

3. 应力平衡分析与优化

3.1 应力平衡历程分析

3.2 入射波优化

3.3 有效应变分析

4. 结论

留言板

低阻抗试样动态加载试验相关问题研究

doi: 10.21656/1000-0887.450279

作者简介: 殷建平(1996—)，男，博士生(E-mail: jpyin@mail.nwpu.edu.cn)

通讯作者: 苗应刚(1983—)，男，副教授，博士，硕士生导师(通讯作者. E-mail: ygmiao@nwpu.edu.cn)

计量

出版历程

Study of Dynamic Loading Tests on Low-Impedance Specimens

0. 引言

1. Hopkinson杆动态加载技术

2. 低幅值透射信号的采集

2.1 高灵敏度半导体应用

2.2 异质透射杆应用

3. 应力平衡分析与优化

3.1 应力平衡历程分析

3.2 入射波优化

3.3 有效应变分析

4. 结论

计量

出版历程

目录

0. 引言

1. Hopkinson杆动态加载技术

2. 低幅值透射信号的采集

2.1 高灵敏度半导体应用

2.2 异质透射杆应用

3. 应力平衡分析与优化

3.1 应力平衡历程分析

3.2 入射波优化

3.3 有效应变分析

4. 结论

作者简介:
殷建平(1996—)，男，博士生(E-mail: jpyin@mail.nwpu.edu.cn)

通讯作者:
苗应刚(1983—)，男，副教授，博士，硕士生导师(通讯作者. E-mail: ygmiao@nwpu.edu.cn)