钢纤维混凝土冲击破坏特性GDEM软件模拟

张金; 戚志刚; 张磊

doi:10.21656/1000-0887.450311

钢纤维混凝土冲击破坏特性GDEM软件模拟

doi: 10.21656/1000-0887.450311

张金^{1, 2,},
戚志刚^{1, 2, 3},
张磊^{1, 2, ,}

1.
目标易损性评估全国重点实验室, 河南洛阳 471023
2.
军事科学院国防工程研究院, 河南洛阳 471000
3.
哈尔滨工程大学航天与建筑工程学院, 哈尔滨 150001

基金项目:

国家自然科学基金 12172381

中原领军人才项目 234200510016

详细信息

作者简介:
张金(1996—)，男，博士生(E-mail: 2743008270@qq.com)

通讯作者:
张磊(1974—)，男，研究员，博士(通讯作者. E-mail: ustczhanglei@163.com)

中图分类号: O331
计量
- 文章访问数: 98
- HTML全文浏览量: 37
- PDF下载量: 21
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-18
- 修回日期: 2025-01-31
- 刊出日期: 2025-05-01

Impact Damage Characteristics Simulation of Steel Fiber Reinforced Concrete With the GDEM Software

ZHANG Jin^{1, 2
,},
QI Zhigang^{1, 2, 3},
ZHANG Lei^{1, 2
, ,}

1.
State Key Laboratory of Target Vulnerability Assessment, Luoyang, Henan 471023, P.R.China
2.
Institute of Defense Engineering, AMS, Luoyang, Henan 471000, P.R.China
3.
College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, P.R.China

摘要

摘要: 钢纤维混凝土(steel fiber reinforced concrete，SFRC)是防护工程中最常用的结构材料，在爆炸、侵彻等强动载作用下，其往往处于高应变率的复杂应力状态. 目前，关于SFRC的动态力学性能的研究大多局限于一维应力和一维应变加载条件下，而关于三向应力状态下的冲击压缩特性研究较少. 该文采用基于连续-非连续介质力学的数值仿真软件GDEM-BlockDyna，模拟了围压对SFRC动态力学性能和破坏模式的影响. 结果表明：围压下SFRC的峰值应力和峰值应变均随着应变率的提高有不同程度的增大，但围压会抑制SFRC冲击压缩强度的率效应. GDEM能较逼真地模拟应变率和围压对材料动态力学的影响，与有限元方法相比，GDEM能够更好地模拟SFRC从完整到破坏的过程及特征，且对SFRC峰值应力后的破坏阶段的描述模拟更加准确.
- 钢纤维混凝土 /
- 主动围压 /
- GDEM /
- 有限元方法 /
- HJC模型
Abstract: Steel fiber-reinforced concrete (SFRC) is the most utilized structural material for protective engineering. It is frequently subjected to complex stress states with high strain rates under strong dynamic loads, such as explosions and penetrations. Most current studies on the dynamic mechanical properties of SFRC are limited to 1D stress and 1D strain loading conditions. However, the impact-compression characteristics under 3D stress states are still scarce. Herein the GDEM-BlockDyna numerical simulation software was employed to simulate the damage modes of SFRC under confining pressures and investigate the concrete dynamic mechanical properties. The results indicate that, the peak stress and peak strain of SFRC both increase to different extents with the strain rates. The confining pressure reduces the rate effect on the impact compression strength of SFRC. The GDEM can realistically simulate the effects of strain rate and confining pressure on the dynamic mechanics of materials. In comparison to the finite element method, the GDEM is more effective in simulating the behaviors of steel fiber reinforced concrete, from its intact state to destruction. Furthermore, the GDEM can accurately describe the destruction stage characteristics of SFRC after the peak stress.
- steel fiber reinforced concrete /
- active confining pressure /
- GDEM /
- finite-element method /
- HJC model

HTML全文

0. 引言

钢纤维混凝土(SFRC)是由细骨料、粗骨料、水泥以及乱向分布的钢纤维组成的一种多相非均质复合材料^[1]，其比普通混凝土具有更高的强度、抗冲击韧性和耐久性^[2]，因而被广泛应用于防护工程中^[3]. SFRC是防护结构最常用的结构材料，在爆炸、侵彻等强动载作用下，其往往处于高应变率的复杂应力状态^[4]. 因此，对SFRC在复杂应力状态下的动态力学性能及失效模式研究，具有重要的工程应用价值.

目前，对复杂应力状态下混凝土类材料在冲击载荷作用下的动态力学性能的研究主要采用带有主动围压装置的Hopkinson压杆，其通过主动围压装置对试件施加侧向等围压状态，即σ₂=σ₃，然后利用Hopkinson压杆对试件进行σ₁方向的冲击加载. 李世超^[5]建立了不同纤维含量(0%，0.75%，1.5%)的SFRC在给定围压和高应变率(59~238 s^-1)下的本构模型. 张磊等^[6]基于Φ100 mm SHPB设计了一套同步对试件预加围压和轴压的装置，并对SFRC围压下率效应等问题进行实验研究. 徐松林等^[7-8]研制了一种真三轴静载作用下混凝土类材料动态实验系统，真正意义上实现了σ₁≠σ₂≠σ₃，并且揭示了混凝土动态破坏强度受到应变率和加载路径的影响规律. Liu等^[9]也采用类似的实验装置研究了砂岩在双轴和三轴压缩下的破坏模式，并采用CT扫描获取了试样的3D损伤图像.

由于混凝土复杂应力状态下冲击实验存在实验成本高、周期长且离散性大等缺点，数值模拟成为重要的技术途径. 目前混凝土材料与结构分析的数值计算方法主要包括三大类^[10]：一类是以连续介质力学为基础，主要包括有限元法(FEM)、有限差分法和边界单元法等；另一类是以非连续介质力学为基础，主要包括块体离散单元法、非连续变形分析(DDA)法、流形元法和颗粒体离散元法等；第三类为连续介质与离散介质相耦合，包括有限元-离散元耦合法、有限差分-离散元耦合法和边界元-离散元耦合法.

Cai等^[11]使用有限元模型模拟了冲击载荷下钢纤维增强混凝土梁的破坏过程，结果表明，通过加入单元的失效准则形成裂纹来模拟破坏的方法受网格影响很大. 对此，许多学者将扩展有限元(XFEM)用于混凝土裂缝开裂模拟中，即在裂纹附近单元上引入不连续位移模式能较好克服分离裂纹模型的网格依赖性^[12]. 但该方法对于裂缝存在分岔、交汇以及三维问题中混凝土裂缝面不光滑情况尚且没有较好的处理方法，且不适用于处理大变形及失稳问题^[13]. 对此，夏才初等^[14]采用DDA算法成功模拟了裂纹的扩展和贯通过程，但DDA算法不能完全反映断续节理破坏前的变形特征，且裂纹扩展路径依赖于离散块体大小^[15]. 基于此，Ning等^[16]用数值流形法(NMM)，将DDA算法与有限元法相结合来模拟岩石的剪切裂纹、拉伸裂纹以及预制裂纹的边坡裂纹扩展滑移等问题. 但是在NMM计算过程中，裂纹尖端受到单元边界的约束，导致裂纹尖端止步于单元内部，从而降低计算精度^[17]. 此外，光滑粒子(SPH)法作为一种无网格方法，其摆脱了对网格的依赖，因此适合处理冲击大变形、断裂、动态裂纹扩展等传统网格难以解决的问题^[18]，但其存在边界处理算法不成熟、计算效率低和收敛速度慢等问题^[19]. 为克服以上问题，发展出了连续与非连续耦合的方法. 学者们采用SPH与有限元法耦合的方法模拟了冲击荷载作用下混凝土结构的动态响应，既可以避免因采用Lagrange网格出现的大变形无法求解的问题，又发挥了网格计算效率高的优势^[20-21]. 马春驰等^[22]采用GDEM软件(基于有限元与离散元相耦合的方法)研究了含节理围岩在不同类型岩爆下的破坏过程.

综上可知，有限元法等能够较好地模拟材料在连续状态下的力学响应，但模拟材料从连续到非连续的破坏过程会存在一定不足，若引入单元删除技术又会导致系统质量和能量不守恒，以及物体几何边界的改变等问题^{[19, 23]}. 块体离散元及颗粒离散元在模拟非连续的运动特性方面具有一定的优势，但难以模拟材料的连续变形过程. 而连续介质与离散介质相耦合的方法结合了上述两种方法的优势，不仅可以模拟材料在连续及非连续状态下的变形、运动特性，更可以模拟材料由连续体到非连续体的渐近破坏过程^[20].

因此，本文采用基于连续介质的离散元方法的数值仿真软件GDEM，探讨了冲击荷载作用下SFRC破裂扩展-贯通的连续-非连续破坏的演化过程，以及围压对SFRC裂纹发育过程的抑制效应.

1. 基于连续-非连续数值模拟方法与模型

1.1 GDEM概述

GDEM-BlockDyna动力学软件以CDEM(continuum discontinuous element method)为计算核心，基于多核CPU进行并行计算. CDEM是一种耦合了FEM/DEM的显式数值模拟方法，其高度融合了连续-非连续显式数值分析方法的特点，并在能量层面实现了有限元、离散元及无网格算法的统一，在模拟弹塑性变形的同时可以模拟显示裂纹在材料中的萌生、扩展及贯通过程.

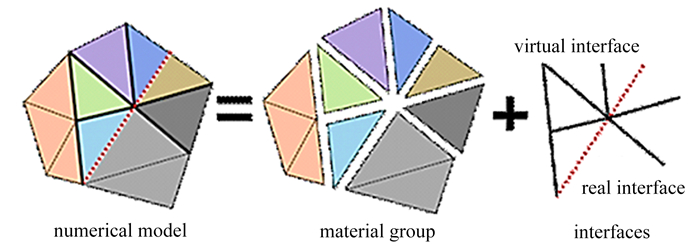
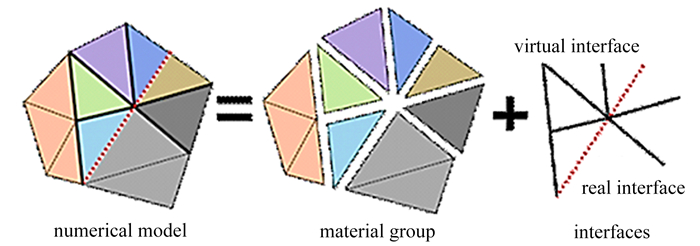
CDEM数值模型由块体和界面两部分组成，其中块体由一个或者多个有限单元组成，用于表征材料的弹性、塑性、损伤等连续特征，如图 1所示. 两个块体公共界面用于表征材料的断裂、滑移、碰撞等非连续特征. 此外，CDEM中界面分为真实界面和虚拟界面，真实界面用于表征材料的交界面、断层、节理等真实的不连续面，其强度参数与正式界面参数一致. 虚拟界面主要有两个作用：①连接两个块体，用于传递力学信息；②为显示裂纹的扩展提供潜在的通道(即裂纹可以沿着任意一个虚拟界面进行扩展). 虚拟界面通过6个弹簧单元与块体接触来传递力学信息，且可以为裂纹的显示扩展和贯通提供通道^[22].

图 1 CDEM中数值模型的构成^[22]

Figure 1. Composition of numerical models in the CDEM^[22]

下载: 全尺寸图片幻灯片

1.2 模型建立

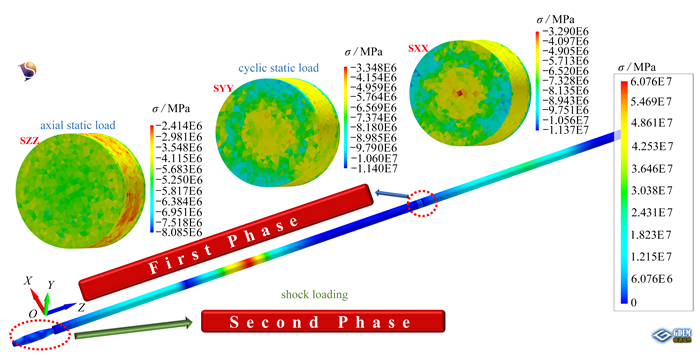
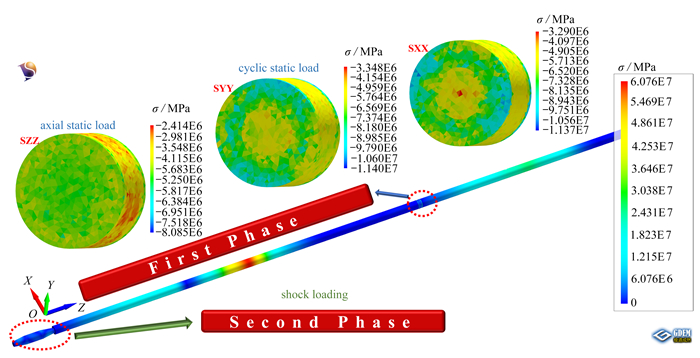
几何模型采用真实模型建立^[6]，结构图如图 2所示：模型主要由纺锤形子弹、入射杆(Φ100 mm×4 500 mm)、试样(Φ100 mm×50 mm)和透射杆(Φ100 mm×2 500 mm)四部分组成；试样网格尺寸为5 mm，其余网格尺寸均为10 mm；透射杆自由端采用无反射边界，分别在入射杆和透射杆中间位置取观测点，提取应变信号.

图 2 模拟计算两阶段

注为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.

Figure 2. Two phases of simulation

下载: 全尺寸图片幻灯片

子弹及杆件单元本构选用线弹性本构，试件选择HJC本构模型. 杆件与试件间接触为Mohr-Coulomb脆性断裂模型，而试件单元间的接触本构选择考虑应变率效应的Mohr-Coulomb脆性断裂模型以模拟试件裂纹萌生、扩展并导致试件破坏的过程. 试件基本力学参数设置见表 1.

表 1 SFRC基本力学参数

Table 1. Basic mechanical parameters of specimens

serial number	density/(g·cm^-3)	elastic modulus/GPa	Poisson’s ratio	cohesion/MPa	tensile strength/MPa	internal friction angle/(°)	swelling angle/(°)
C15	2 480	21.8	0.23	10	1.57	36.5	0
C30	2 500	38	0.21	27	4.19	37.4	0
C60	2 636	44	0.20	32	5.49	37.9	0
C80	2 645	48	0.19	45	8.34	38.9	0

下载: 导出CSV

| 显示表格

为模拟围压冲击加载过程，模型计算过程分为两个阶段：第一阶段0~2 000步时为轴向静载和环向静载加载阶段；第二阶段2 000~16 000步时为动态加载阶段.

第一阶段施加应力边界条件，计算到收敛稳定，构造初始SFRC应力环境.

第二阶段动态加载阶段计算. 构建几何模型时，对子弹部分的块体单元进行组号设定，当进入动态加载阶段时，脚本命令给代表子弹的单元组号施加速度，从而实现对围压下SFRC的动态加载，如图 2所示.

1.3 模拟方案

试件为含1%钢纤维的C15、C30、C60、C80的SFRC. 单轴SHPB冲击实验利用100 mm SHPB进行，子弹撞击速度分别为5 m/s，10 m/s，15 m/s和20 m/s. 主动围压实验的围压大小分别为5 MPa，15 MPa和20 MPa，撞击速度与单轴SHPB实验相同.

1.3.1 模拟参数

材料参数如表 2所示.

表 2 SFRC-HJC参数

Table 2. Steel fiber reinforced concrete HJC parameters

serial number	ρ	G/Pa	A	B	C	N	f_c/Pa	T/Pa	EFMIN	S_max
C15	2 480	8.9E9	0.79	1.6	0.007	0.61	1.9E7	1.5E6	0.01	7
C30	2 500	1.5E10	0.79	1.6	0.007	0.61	5.0E7	4.2E6	0.01	7
C60	2 636	1.8E10	0.79	1.6	0.007	0.61	6.6E7	5.5E6	0.01	7
C80	2 645	2.0E10	0.79	1.6	0.007	0.61	1.0E8	8.3E6	0.01	7

serial number	P_crush/Pa	μ_crush	P_lock/Pa	μ_lock	D₁	D₂	K₁/Pa	K₂/Pa	K₃/Pa
C15	6.3E6	0.001	6.0E8	0.1	0.04	1	8.5E10	-1.71E11	2.08E11
C30	1.6E7	0.001	1.0E9	0.1	0.04	1	8.5E10	-1.71E11	2.08E11
C60	2.2E7	0.001	1.2E9	0.1	0.04	1	8.5E10	-1.71E11	2.08E11
C80	3.3E7	0.001	1.3E9	0.1	0.04	1	8.5E10	-1.71E11	2.08E11

下载: 导出CSV

| 显示表格

2. 模拟结果与分析

2.1 破坏形态模拟效果

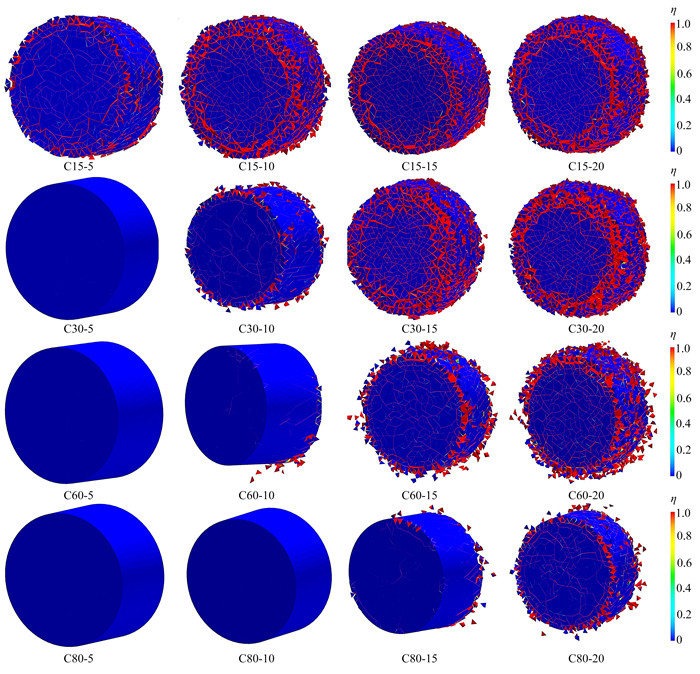
图 3为SFRC在四种速度(5 m/s，10 m/s，15 m/s和20 m/s)下单轴冲击破坏形态的损伤云图，其损伤情况取决于试件的强度和撞击速度. 在撞击速度较低或者试件强度较高时，损伤表现为在试件周边出现细小的裂纹而试件中部尚未出现裂纹；随撞击速度提高，作用在试件上的冲击载随之增加，试件外缘的裂纹扩展汇聚贯通，周边出现剥离，试件中部出现较为密集的裂纹，但试件中部没有散裂. 可见，在冲击载荷作用下，试件截面方向的损伤分布并不均匀，靠近外侧部位的损伤比试件中部更为严重.

图 3 SFRC动态单轴压缩损伤云图

Figure 3. Dynamic uniaxial compression damage contours for SFRC

下载: 全尺寸图片幻灯片

根据SFRC受到冲击压缩荷载后的破坏形态，可将SFRC在动载下的受压损伤程度分为三种：①试件外侧出现少数宏观裂缝并保持完整；②试件外侧出现大量宏观裂缝但未完全粉碎，且靠近中心位置完整，即存在“留芯”现象；③随着冲击压缩荷载的增大，“留芯”区逐渐减小，宏观裂缝数量急剧增大并沿径向和轴向相互贯通，试样碎裂并伴有大量碎片飞溅，这种沿圆柱体试件径向不同位置损伤分布存在差异的现象是由于材料的Poisson效应而引起的横向惯性效应，对试件形成径向的侧限应力，不同位置的径向约束不同，从而使得试件横截面的不同位置上出现的损伤积累情况不同，并由此导致不同的宏观破坏情况. 在冲击压缩载荷作用下，SFRC内部受到侧向变形的限制，内部类似处于三向应力状态并且越靠近内侧所受惯性效应的影响越明显，因此在损伤云图中SFRC外部损伤程度远大于内部.

图 4为C60-SFRC在不同速度下冲击破坏的模拟结果与文献[24]中的实验结果. 由图可知，模拟结果能较好地反映SFRC在动载下受压损伤的三种情况，且与文献结果相近.

图 4 C60-SFRC单轴冲击破坏模拟损伤结果云图与文献结果^[24]

Figure 4. SFRC uniaxial impact damage simulation damage result contours and experimental results^[24]

下载: 全尺寸图片幻灯片

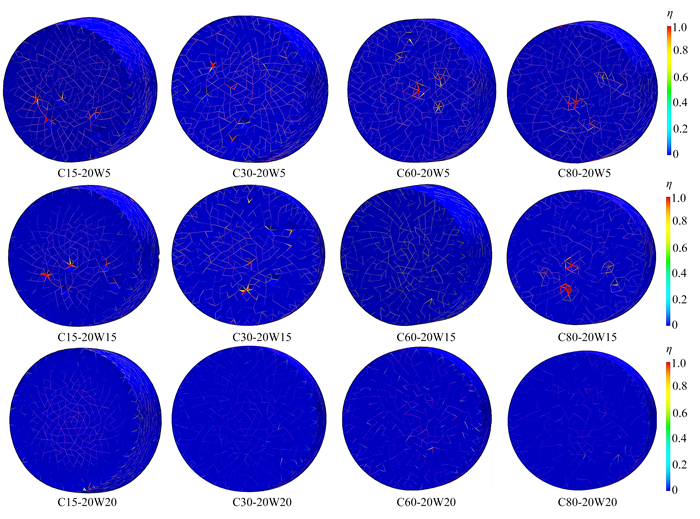
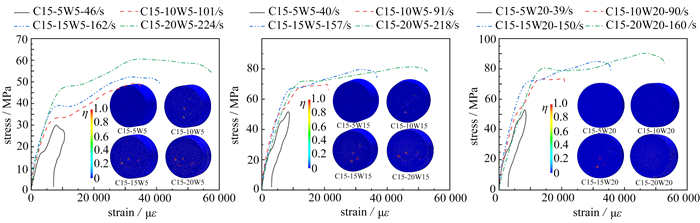
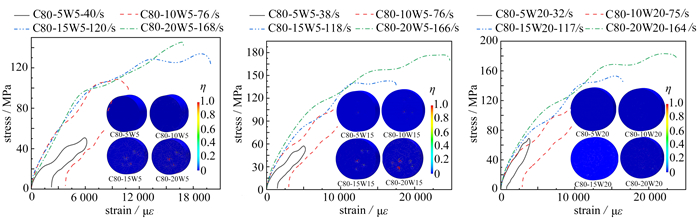
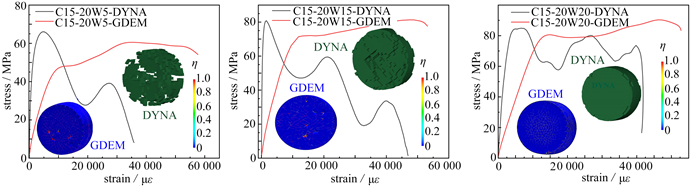
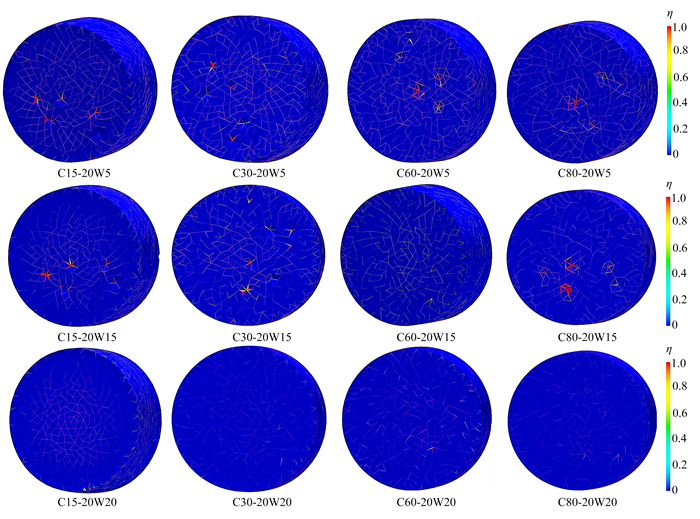
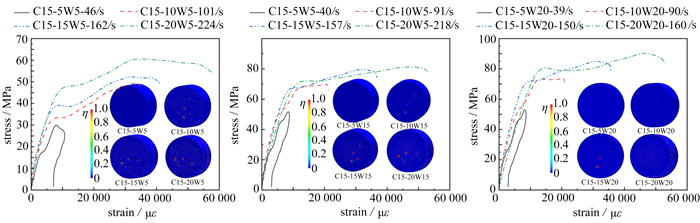
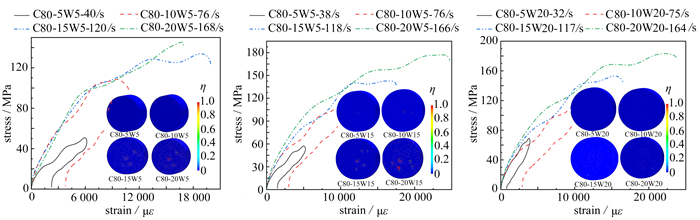
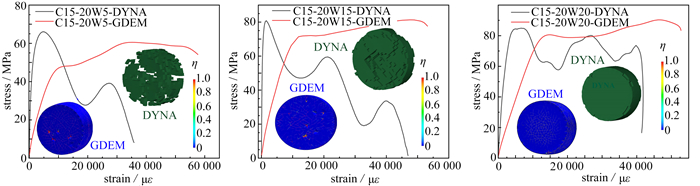
主动围压SHPB实验结果表明，存在围压时SFRC损伤云图与单轴情况下的破坏有明显不同. 图 5为四种强度SFRC在三种围压下的动态冲击破坏结果图. 图中编号C15-20W5，其中C15表示SFRC强度，第二位数字20代表冲击速度为20 m/s，W5代表围压(环向-轴向)为5 MPa，其他类似.

图 5 围压下SFRC损伤云图

Figure 5. SFRC damage contours under circumferential pressure

下载: 全尺寸图片幻灯片

图 5为SFRC在围压下动态加载后的损伤云图，与单轴加载SFRC沿四周拉伸剥落破坏明显不同，SFRC受围压影响侧向没有飞散的碎块，整体性较好. 围压下SFRC损伤云图结果表明：随着围压的增大四种强度SFRC在相同冲击速度下均表现为裂纹数量的减少，即围压能有效限制裂纹的扩展. 此外，围压弱化了SFRC内部的薄弱区，使得内部裂纹的发展比单轴加载下更均匀.

2.2 围压和应变率对SFRC应力-应变曲线的影响

2.2.1 典型的波形

根据一维应力波理论，我们利用实验测得应变信号，得到多孔混凝土试件变形过程中随时间变化的应力、应变和应变率，二波法公式如下：

$\left\{\begin{array}{l} \sigma_{\mathrm{s}}(t)=\frac{E A_{0}}{A_{\mathrm{s}}} \varepsilon_{\mathrm{t}}(t) , \\ \varepsilon_{\mathrm{s}}(t)=\frac{2 C_{0}}{l_{\mathrm{s}}} \int_{0}^{t}\left[\varepsilon_{i}(t)-\varepsilon_{\mathrm{t}}(t)\right] \mathrm{d} t ,\\ \dot{\varepsilon}_{\mathrm{s}}(t)=\frac{2 C_{0}}{l_{\mathrm{s}}}\left[\varepsilon_{i}(t)-\varepsilon_{\mathrm{t}}(t)\right], \end{array}\righ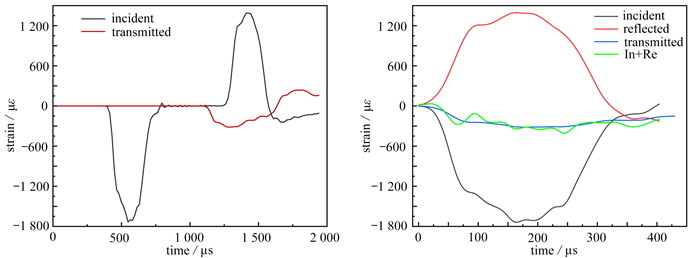t.$

(1)

式中，E为压杆弹性模量，C₀为压杆的弹性波速，A₀为压杆截面积，A_s为试样截面积，l_s为试样长度，σ_s(t)为平均应力，ε_s(t)为平均应变， $\dot{\varepsilon}_{\mathrm{s}}(t)$ 为平均应变率.

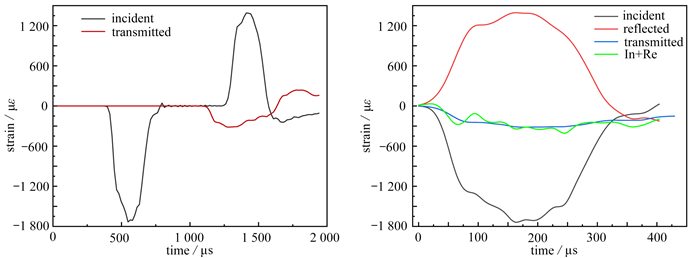
图 6为典型的入射波-透射波波形以及应力平衡图. 由图可知，入射波+反射波能与透射波较好吻合，表明试验过程中能较好地满足应力均匀性假定.

图 6 入射波-透射波波形和应力平衡

Figure 6. Incident-transmitted waveforms and stress balance diagrams

下载: 全尺寸图片幻灯片

2.2.2 SFRC应力-应变曲线

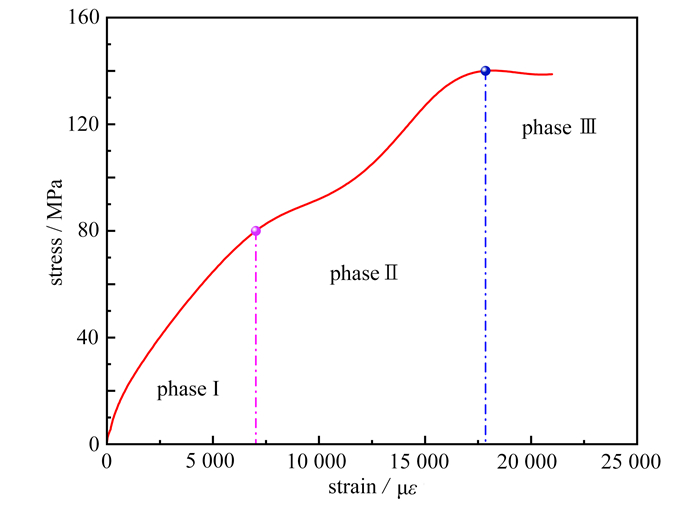
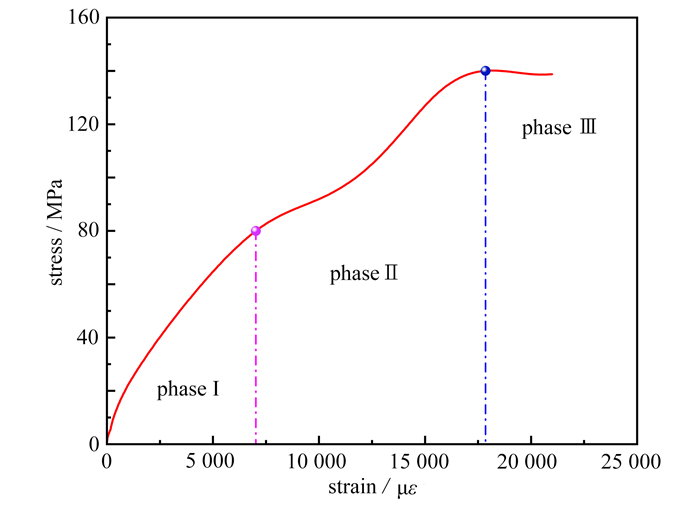
图 7为典型的围压下SFRC应力-应变曲线. 采用CDEM模型计算出的应力-应变结果可以分为三个阶段，即弹性阶段、流动阶段、失效阶段. 加载初期，围压阻碍和延缓了SFRC内部裂缝、缺陷的形成和扩展，因此线弹性阶段，SFRC处于初始压密和弹性增长的过程，应力-应变曲线表现为有大幅增长，此阶段围压促进了SFRC的致密化，但未出现明显的结构性损伤. 而随着载荷的增大，SFRC进入第二阶段，此时试样处于非线性变形阶段，SFRC内部裂纹萌生、扩展，此阶段损伤稳定积累. 第三阶段，SFRC内部损伤区加速增长，微裂纹扩展贯通后形成宏观裂纹，试样到达峰值应力，但受围压影响，峰值应力后，SFRC应力-应变曲线表现为平稳的下降曲线，表现出较高的残余强度.

图 7 围压下典型的SFRC应力-应变曲线

Figure 7. Typical SFRC stress-strain curves under circumferential pressure

下载: 全尺寸图片幻灯片

图 8、图 9为试样在三种围压和冲击速度分别为5 m/s，10 m/s，15 m/s和20 m/s时的轴向应力-应变曲线. 5 m/s时SFRC局部有微裂纹，峰值应力后卸载，应力-应变曲线具有明显的应变滞后现象，表明混凝土的黏弹塑性特征. 在较高的两个速度下，SFRC发生破坏，峰值应力后出现不明显的应变软化现象，其残余强度较高. 在三轴压缩的试验中，随着围压的增大，三轴曲线峰后段下降缓慢，破坏后仍具有较高的峰后残余强度，表现出很强的整体特征.

图 8 不同围压下应变率对C15-SFRC应力-应变曲线影响规律

Figure 8. Influences of strain rates on stress-strain curves of C15-SFRC under different confining pressures

下载: 全尺寸图片幻灯片

图 9 不同围压下应变率对C80-SFRC应力-应变曲线影响规律

Figure 9. Influences of strain rates on stress-strain curves of C80-SFRC under different confining pressures

下载: 全尺寸图片幻灯片

横向对比强度为C15和C80的SFRC试件在冲击速度相同而围压不同时的轴向应力-应变曲线，随着围压的增大，围压对材料裂纹发育的抑制效果显著，峰值应力和峰值应变都有明显提高，即围压具有明显的增强和增韧效果.

2.3 应变率对SFRC强度的影响

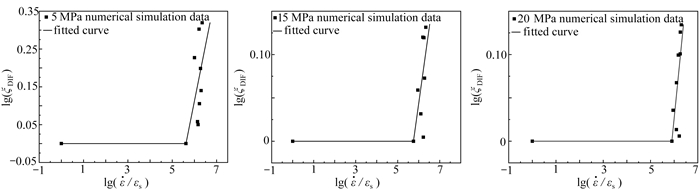
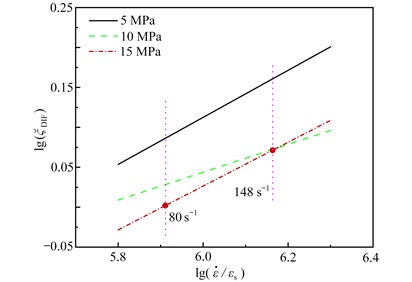
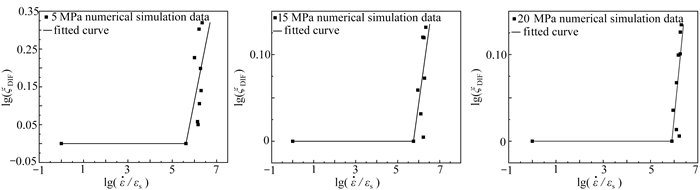
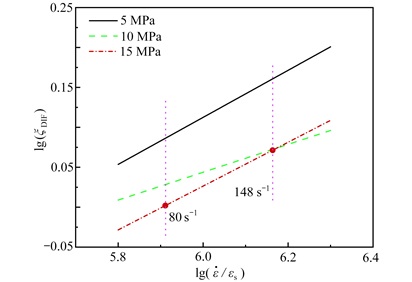
采用 $\xi_{\mathrm{DIF}}=\sigma_{\mathrm{dP}} / \sigma_{\mathrm{sp}}$ 来描述材料强度的应变率效应，其中 $\sigma_{\mathrm{dp}}$ 为主动围压SHPB动态强度， $\sigma_{\mathrm{sp}}$ 为常规三轴实验准静态强度。并假定在低应变率段 $\dot{\varepsilon} \leqslant \kappa, \kappa$ 为转折应变率. 对高应变率段，采用幂函数形式拟合，拟合方程见式(2)，拟合结果见图 10.

图 10 三种围压下

$\operatorname{SFRC} \lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ 拟合曲线

Figure 10. SFRC

$\lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ fitting curves under 3 types of confining pressures

下载: 全尺寸图片幻灯片

图 11为三种围压下的拟合曲线，在80~148 s^-1的应变率范围内，SFRC的DIF值随着围压的增大而减小，即围压对SFRC具有明显的率效应抑制作用. 究其原因，径向围压可有效阻止横向裂纹的扩展速度，降低了失稳裂纹的数量，从而减小了由裂纹扩展惯性而引起的强度增加，所以此时SFRC的动态增强效应会随着围压增大而减小.

$\lg \left(\xi_{\mathrm{DIF}}\right)= \begin{cases}-1.655+0.294 \lg \left(\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{\mathrm{s}}}\right), & \sigma_{3}=5 \mathrm{MPa} ,\\ -1.002+0.174 \lg \left(\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{\mathrm{s}}}\right), & \sigma_{3}=15 \mathrm{MPa} ,\\ -1.620+0.274 \lg \left(\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{\mathrm{s}}}\right), & \sigma_{3}=20 \mathrm{MPa}.\end{cases}$

(2)

图 11 三种围压下

$\lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ 拟合曲线

Figure 11. Fitted curves of

$\lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ at 3 confining pressures

下载: 全尺寸图片幻灯片

2.4 GDEM软件与有限元模拟结果对比分析

基于有限元软件DYNA进行数值模拟，采用3D Solid 164单元建立模型，有限元模型共分为入射杆、透射杆和试件三个部分，材料参数与GDEM模拟中参数相同. 子弹、入射杆和透射杆材料采用MAT_ELASTIC，SFRC采用MAT_JOHNSON_HOLMQUIST_ CONCRETE. 模型透射杆底端设置无反射边界条件，压杆与试件之间的接触算法定义为面面接触(surface-to-surface contact)，为无摩擦的光滑接触面. 单元失效控制采用侵蚀失效准则，当单元发生失效，单元的应力变为零值，不再与其他单元有相互作用，在后处理可视化图像上的表征为单元消失.

由于低强度混凝土在冲击载荷下的单元删除现象更为明显，因此以C15的SFRC为例. 图 12为低围压下有限元计算结果，试样中大量单元在冲击过程中失效删除，此时试件已经发生结构性破坏，不再是一个连续体，而表征应力曲线形状的透射波波形会发生变化，即体现在峰值应力后应力-应变曲线会有明显的下降，反映出试件在短时间内失去承载能力. 而实际上围压条件下，试件在峰值应力后仍具有一定的承载能力，而并非短时间内失效.

图 12 有限元结果与GDEM模拟结果对比

Figure 12. Comparison between finite element results and GDEM simulation results

下载: 全尺寸图片幻灯片

随着围压的增大，C15试样在相同冲击速度下因失效删除的单元数量减少，其应力峰值后的应力-应变曲线部分下降速度减缓，与实际情况更相符. 因此，在采用有限元方法模拟时，在强度极限后的下降段，模拟结果很难和实验结果有较好的吻合. 因此，有限元计算结果只能表征试件初始破坏时的形态，而在试件发生单元删除之后的结果，从有限元原理的角度来看是不可信的.

而GDEM软件可以描述材料从连续到非连续的逐步破坏过程，有效避免了删除单元造成的系统质量和能量不守恒以及物体几何边界的改变等问题，从而有效模拟了峰值应力后的变形过程，并使得峰值后应力-应变曲线与实际情况更吻合(如图 12所示).

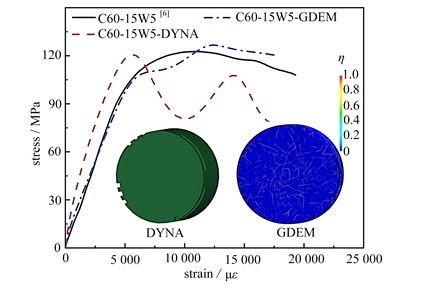
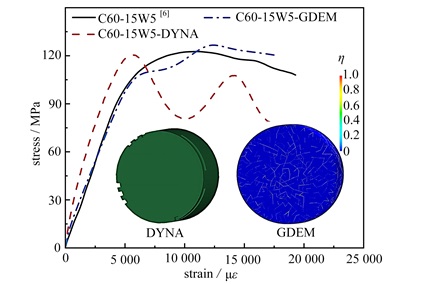
为验证GDEM模拟结果，基于C60-15W5 SFRC，分别将GDEM模拟结果、有限元模拟结果与文献结果^[6]进行对比，如图 13所示. 有限元方法中，由于C60-SFRC具有较高的强度，其在动态冲击过程中单元删除数量较少，使得其在峰值应力后的应变软化现象相比于低围压下C15-SFRC有所缓和，但峰值应力后的波动段与实验结果有一定差距，因而不能真实反映SFRC失效后残余强度的变化. 而GDEM模拟结果完整描述了SFRC在动态载荷下完整-失效的过程，并且GDEM模拟的残余强度结果与实验值相近.

图 13 C60-SFRC实验结果、有限元结果、GDEM软件数值仿真结果对比

Figure 13. Comparison of C60-SFRC experimental results, finite element results and GDEM software numerical results

下载: 全尺寸图片幻灯片

3. 结论

本文采用GDEM软件对围压下SFRC动态冲过程中所表现的率效应和围压效应进行了研究，并与DYNA软件的仿真结果对比，所得结论如下：

1) SHPB单轴冲击加载下，SFRC试件在惯性效应作用下内部处于三向应力状态，抑制了内部裂纹的扩展. 主动围压作用下，SFRC试件内部横向裂纹的扩展得到有效限制，提高了材料的塑性，材料在失效阶段仍具有较高的残余强度.

2) 随围压的增大，材料动态峰值应力和峰值应变都有明显提高，材料在围压下具有明显的增强和增韧效果，并且围压越高时应变率敏感性越低.

3) DYNA软件中的单元删除功能会使得模拟结果中应力峰值后的部分存在较大误差；GDEM软件能较好模拟材料完整-破坏的过程，且峰值后应力-应变曲线更接近实验结果.

图 1 CDEM中数值模型的构成^[22]

Figure 1. Composition of numerical models in the CDEM^[22]

下载: 全尺寸图片幻灯片

图 2 模拟计算两阶段

注为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.

Figure 2. Two phases of simulation

下载: 全尺寸图片幻灯片

图 3 SFRC动态单轴压缩损伤云图

Figure 3. Dynamic uniaxial compression damage contours for SFRC

下载: 全尺寸图片幻灯片

图 4 C60-SFRC单轴冲击破坏模拟损伤结果云图与文献结果^[24]

Figure 4. SFRC uniaxial impact damage simulation damage result contours and experimental results^[24]

下载: 全尺寸图片幻灯片

图 5 围压下SFRC损伤云图

Figure 5. SFRC damage contours under circumferential pressure

下载: 全尺寸图片幻灯片

图 6 入射波-透射波波形和应力平衡

Figure 6. Incident-transmitted waveforms and stress balance diagrams

下载: 全尺寸图片幻灯片

图 7 围压下典型的SFRC应力-应变曲线

Figure 7. Typical SFRC stress-strain curves under circumferential pressure

下载: 全尺寸图片幻灯片

图 8 不同围压下应变率对C15-SFRC应力-应变曲线影响规律

Figure 8. Influences of strain rates on stress-strain curves of C15-SFRC under different confining pressures

下载: 全尺寸图片幻灯片

图 9 不同围压下应变率对C80-SFRC应力-应变曲线影响规律

Figure 9. Influences of strain rates on stress-strain curves of C80-SFRC under different confining pressures

下载: 全尺寸图片幻灯片

三种围压下 $\operatorname{SFRC} \lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ 拟合曲线

SFRC $\lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ fitting curves under 3 types of confining pressures

下载: 全尺寸图片幻灯片

三种围压下 $\lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ 拟合曲线

Fitted curves of $\lg \left(\xi_{\text {DIF }}\right)-\lg \left(\dot{\varepsilon} / \varepsilon_{\mathrm{s}}\right)$ at 3 confining pressures

下载: 全尺寸图片幻灯片

图 12 有限元结果与GDEM模拟结果对比

Figure 12. Comparison between finite element results and GDEM simulation results

下载: 全尺寸图片幻灯片

图 13 C60-SFRC实验结果、有限元结果、GDEM软件数值仿真结果对比

Figure 13. Comparison of C60-SFRC experimental results, finite element results and GDEM software numerical results

下载: 全尺寸图片幻灯片

表 1 SFRC基本力学参数

Table 1. Basic mechanical parameters of specimens

serial number	density/(g·cm^-3)	elastic modulus/GPa	Poisson’s ratio	cohesion/MPa	tensile strength/MPa	internal friction angle/(°)	swelling angle/(°)
C15	2 480	21.8	0.23	10	1.57	36.5	0
C30	2 500	38	0.21	27	4.19	37.4	0
C60	2 636	44	0.20	32	5.49	37.9	0
C80	2 645	48	0.19	45	8.34	38.9	0

下载: 导出CSV

表 2 SFRC-HJC参数

Table 2. Steel fiber reinforced concrete HJC parameters

serial number	ρ	G/Pa	A	B	C	N	f_c/Pa	T/Pa	EFMIN	S_max
C15	2 480	8.9E9	0.79	1.6	0.007	0.61	1.9E7	1.5E6	0.01	7
C30	2 500	1.5E10	0.79	1.6	0.007	0.61	5.0E7	4.2E6	0.01	7
C60	2 636	1.8E10	0.79	1.6	0.007	0.61	6.6E7	5.5E6	0.01	7
C80	2 645	2.0E10	0.79	1.6	0.007	0.61	1.0E8	8.3E6	0.01	7

serial number	P_crush/Pa	μ_crush	P_lock/Pa	μ_lock	D₁	D₂	K₁/Pa	K₂/Pa	K₃/Pa
C15	6.3E6	0.001	6.0E8	0.1	0.04	1	8.5E10	-1.71E11	2.08E11
C30	1.6E7	0.001	1.0E9	0.1	0.04	1	8.5E10	-1.71E11	2.08E11
C60	2.2E7	0.001	1.2E9	0.1	0.04	1	8.5E10	-1.71E11	2.08E11
C80	3.3E7	0.001	1.3E9	0.1	0.04	1	8.5E10	-1.71E11	2.08E11

下载: 导出CSV

参考文献(24)

[1]	刘永胜, 王肖钧, 金挺, 等. 钢纤维混凝土力学性能和本构关系研究[J]. 中国科学技术大学学报, 2007, 37 (7): 717-723. LIU Yongsheng, WANG Xiaojun, JIN Ting, et al. Study on the mechanical properties and constitutive relation of steel fiber reinforced concrete[J]. Journal of University of Science and Technology of China, 2007, 37 (7): 717-723. (in Chinese)
[2]	宁鹏博, 刘军, 赵硕, 等. 钢纤维增强混凝土动态力学性能及HJC本构模型参数标定[J]. 中国建材科技, 2024, 33 (3): 20-25. NING Pengbo, LIU Jun, ZHAO Shou, et al. Dynamic mechanical properties of steel fiber reinforced concrete and parameter calibration of HJC constitutive model[J]. China Building Materials Science & Technology, 2024, 33 (3): 20-25. (in Chinese)
[3]	杨石刚, 罗泽, 许继恒, 等. 侵彻爆炸作用下钢纤维混凝土结构的破坏模式[J]. 爆炸与冲击, 2024, 44 (1): 151-163. YANG Shigang, LUO Ze, XU Jiheng, et al. Failure modes of concrete structure under penetration and explosion[J]. Explosion and Shock Waves, 2024, 44 (1): 151-163. (in Chinese)
[4]	张磊, 郝龙, 项笑炎. 主动围压下钢纤维混凝土动态力学性能研究[C]//第五届全国强动载效应及防护学术会议暨复杂介质/结构的动态力学行为创新研究群体学术研讨会. 呼和浩特, 2013. ZHANG Lei, HAO Long, XIANG Xiaoyan. Study on the dynamic mechanical properties of steel fiber reinforced concrete under confining pressure[C]//The 5 th National Academic Conference on Strong Dynamic Load Effect and Protection and the Group Academic Seminar on Innovative Research on Dynamic Mechanical Behavior of Complex Media/Structures. Hohhot, 2013. (in Chinese)
[5]	李世超. 钢纤维混凝土的静动态力学性能研究[D]. 南京: 南京理工大学, 2019. LI Shichao. Study on static and dynamic mechanical properties of steel fiber reinforced concrete[D]. Nanjing: Nanjing University of Science & Technology, 2019. (in Chinese)
[6]	张磊, 任新见, 郝龙. 围压下钢纤维混凝土冲击动力学性能研究[J]. 兵工学报, 2014, 35 (S2): 275-280. ZHANG Lei, REN Xinjian, HAO Long. Study of the impact dynamic mechanical properties of steel fiber reinforced concrete under confining pressure [J]. Acta Armamentarii, 2014, 35 (S2): 275-280. (in Chinese)
[7]	徐松林, 单俊芳, 王鹏飞, 等. 三轴应力状态下混凝土的侵彻性能研究[J]. 爆炸与冲击, 2019, 39 (7): 4-11. XU Songlin, SHAN Junfang, WANG Pengfei, et al. Penetration performance of concrete under triaxial stress[J]. Explosion and Shock Waves, 2019, 39 (7): 4-11. (in Chinese)
[8]	徐松林, 王鹏飞, 赵坚, 等. 基于三维Hopkinson杆的混凝土动态力学性能研究[J]. 爆炸与冲击, 2017, 37 (2): 180-185. XU Songlin, WANG Pengfei, ZHAO Jian, et al. Dynamic behavior of concrete under static triaxial loading using 3D-Hopkinson bar[J]. Explosion and Shock Waves, 2017, 37 (2): 180-185. (in Chinese)
[9]	LIU K, ZHANG Q B, WU G, et al. Dynamic mechanical and fracture behaviour of sandstone under multiaxial loads using a triaxial Hopkinson bar[J]. Rock Mechanics and Rock Engineering, 2019, 52 (7): 2175-2195. doi: 10.1007/s00603-018-1691-y
[10]	张楚汉. 论岩石、混凝土离散-接触-断裂分析[J]. 岩石力学与工程学报, 2008, 27 (2): 217-235. ZHANG Chuhan. Discrete-contact-fracture analysis of rock and concrete[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (2): 217-235. (in Chinese)
[11]	CAI B, LU S, FU F. Behavior of steel fiber-reinforced coal gangue concrete beams under impact load[J]. Engineering Structures, 2024, 314 : 118306. doi: 10.1016/j.engstruct.2024.118306
[12]	仇杰峰. 混凝土相场损伤模型与扩展有限元方法对比研究[D]. 广州: 华南理工大学, 2019. QIU Jiefeng. Comparative study of phase-field regularized cohesive zone model and extended finite element method in concrete[D]. Guangzhou: South China University of Technology, 2019. (in Chinese)
[13]	刘泉声, 刘学伟. 多场耦合作用下岩体裂隙扩展演化关键问题研究[J]. 岩土力学, 2014, 35 (2): 305-320. LIU Quansheng, LIU Xuewei. Research on critical problem for fracture network propagation and evolution with multifield coupling of fractured rock mass[J]. Rock and Soil Mechanics, 2014, 35 (2): 305-320. (in Chinese)
[14]	夏才初, 许崇帮. 非连续变形分析(DDA)中断续节理扩展的模拟方法研究和试验验证[J]. 岩石力学与工程学报, 2010, 29 (10): 2027-2033. XIA Caichu, XU Chongbang. Study of fracturing algorithm of intermittent joint by DDA and experimental validation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29 (10): 2027-2033. (in Chinese)
[15]	NING Y, YANG J, AN X, et al. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework[J]. Computers and Geotechnics, 2011, 38 (1): 40-49. doi: 10.1016/j.compgeo.2010.09.003
[16]	NING Y J, AN X M, MA G W. Footwall slope stability analysis with the numerical manifold method[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48 (6): 964-975. doi: 10.1016/j.ijrmms.2011.06.011
[17]	李铮, 郭德平, 周小平, 等. 模拟岩石中裂纹扩展连接的近场动力学方法[J]. 岩土力学, 2019, 40 (12): 4711-4721. LI Zheng, GUO Deping, ZHOU Xiaoping, et al. Numerical simulation of crack propagation and coalescence using peridynamics[J]. Rock and Soil Mechanics, 2019, 40 (12): 4711-4721. (in Chinese)
[18]	卞梁. 高速碰撞中的SPH方法及其应用研究[D]. 合肥: 中国科学技术大学, 2009. BIAN Liang. The SPH method and its application in hypervelocity impact[D]. Hefei: University of Science and Technology of China, 2009. (in Chinese)
[19]	肖毅华. 有限元法与光滑粒子法的耦合算法研究[D]. 长沙: 湖南大学, 2012. XIAO Yihua. Study on coupling algorithm of finite element method and smoothed particle hydrodynamics[D]. Changsha: Hunan University, 2012. (in Chinese)
[20]	王帅. 基于FEM/SPH方法的水下爆炸冲击荷载作用下的混凝土重力坝破坏模式研究[D]. 天津: 天津大学, 2012. WANG Shuai. Research on the failure mode of the concrete gravity dam under blast loading based on FEM/SPH coupling method[D]. Tianjin: Tianjin University, 2012. (in Chinese)
[21]	纪冲, 龙源, 方向. 基于FEM-SPH耦合法的弹丸侵彻钢纤维混凝土数值模拟[J]. 振动与冲击, 2010, 29 (7): 69-74. JI Chong, LONG Yuan, FANG Xiang. Numerical simulation for projectile penetrating steel fiber reinforced concrete with FEM-SPH coupling algorithm[J]. Journal of Vibration and Shock, 2010, 29 (7): 69-74. (in Chinese)
[22]	马春驰, 陈柯竹, 李天斌, 等. 基于GDEM的应力-结构型岩爆数值模拟研究[J]. 隧道与地下工程灾害防治, 2020, 2 (3): 85-94. MA Chunchi, CHEN Kezhu, LI Tianbin, et al. Numerical simulation of stress-structural rockburst based on GDEM software[J]. Hazard Control in Tunnelling and Underground Engineering, 2020, 2 (3): 85-94. (in Chinese)
[23]	孔祥振, 方秦. 基于SPH方法对强动载下混凝土结构损伤破坏的数值模拟研究[J]. 中国科学: 物理学力学天文学, 2020, 50 (2): 25-33. KONG Xiangzhen, FANG Qin. Numerical predictions of failures in concrete structures subjected to intense dynamic loadings using the smooth particle hydrodynamics method[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2020, 50 (2): 25-33. (in Chinese)
[24]	郝龙. 围压状态下钢纤维混凝土试件动态力学性能的试验研究[D]. 南京: 河海大学, 2013. HAO Long. The experiment study on the dynamic mechanical properties of steel fiber reinforced concrete specimen with confining pressure[D]. Nanjing: Hohai University, 2013. (in Chinese)

施引文献

资源附件(0)

访问统计

图(13) / 表(2)

计量

文章访问数: 98
HTML全文浏览量: 37
PDF下载量: 21
被引次数: 0

0. 引言
1. 基于连续-非连续数值模拟方法与模型
1.1 GDEM概述
1.2 模型建立
1.3 模拟方案
2. 模拟结果与分析
2.1 破坏形态模拟效果
2.2 围压和应变率对SFRC应力-应变曲线的影响
2.3 应变率对SFRC强度的影响
2.4 GDEM软件与有限元模拟结果对比分析
3. 结论

0. 引言
1. 基于连续-非连续数值模拟方法与模型
1.1 GDEM概述
1.2 模型建立
1.3 模拟方案
2. 模拟结果与分析
2.1 破坏形态模拟效果
2.2 围压和应变率对SFRC应力-应变曲线的影响
2.3 应变率对SFRC强度的影响
2.4 GDEM软件与有限元模拟结果对比分析
3. 结论

参考文献(24)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

钢纤维混凝土冲击破坏特性GDEM软件模拟

doi: 10.21656/1000-0887.450311

作者简介:
张金(1996—)，男，博士生(E-mail: 2743008270@qq.com)

通讯作者:
张磊(1974—)，男，研究员，博士(通讯作者. E-mail: ustczhanglei@163.com)

计量

Impact Damage Characteristics Simulation of Steel Fiber Reinforced Concrete With the GDEM Software

0. 引言

1. 基于连续-非连续数值模拟方法与模型

1.1 GDEM概述

1.2 模型建立

1.3 模拟方案

1.3.1 模拟参数

2. 模拟结果与分析

2.1 破坏形态模拟效果

2.2 围压和应变率对SFRC应力-应变曲线的影响

2.2.1 典型的波形

2.2.2 SFRC应力-应变曲线

2.3 应变率对SFRC强度的影响

2.4 GDEM软件与有限元模拟结果对比分析

3. 结论

计量

目录

0. 引言

1. 基于连续-非连续数值模拟方法与模型

1.1 GDEM概述

1.2 模型建立

1.3 模拟方案

2. 模拟结果与分析

2.1 破坏形态模拟效果

2.2 围压和应变率对SFRC应力-应变曲线的影响

2.3 应变率对SFRC强度的影响

2.4 GDEM软件与有限元模拟结果对比分析

3. 结论

留言板

钢纤维混凝土冲击破坏特性GDEM软件模拟

doi: 10.21656/1000-0887.450311

作者简介: 张金(1996—)，男，博士生(E-mail: 2743008270@qq.com)

通讯作者: 张磊(1974—)，男，研究员，博士(通讯作者. E-mail: ustczhanglei@163.com)

计量

出版历程

Impact Damage Characteristics Simulation of Steel Fiber Reinforced Concrete With the GDEM Software

0. 引言

1. 基于连续-非连续数值模拟方法与模型

1.1 GDEM概述

1.2 模型建立

1.3 模拟方案

1.3.1 模拟参数

2. 模拟结果与分析

2.1 破坏形态模拟效果

2.2 围压和应变率对SFRC应力-应变曲线的影响

2.2.1 典型的波形

2.2.2 SFRC应力-应变曲线

2.3 应变率对SFRC强度的影响

2.4 GDEM软件与有限元模拟结果对比分析

3. 结论

计量

出版历程

目录

0. 引言

1. 基于连续-非连续数值模拟方法与模型

1.1 GDEM概述

1.2 模型建立

1.3 模拟方案

2. 模拟结果与分析

2.1 破坏形态模拟效果

2.2 围压和应变率对SFRC应力-应变曲线的影响

2.3 应变率对SFRC强度的影响

2.4 GDEM软件与有限元模拟结果对比分析

3. 结论

作者简介:
张金(1996—)，男，博士生(E-mail: 2743008270@qq.com)

通讯作者:
张磊(1974—)，男，研究员，博士(通讯作者. E-mail: ustczhanglei@163.com)